Jupiter Calendar
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Desert Skies – October
Desert Skies Tucson Amateur Astronomy Association Volume LIV, Number 10 October, 2008 Mount Lemmon SkyCenter Learn about: ♦ Progress on TIMPA Observatory ♦ The new electronic newsletter! ♦ TAAA Astronomy Complex Update ♦ Volunteer for School star parties ♦ Articles from our members ♦ Websites: Trips On The Internet ♦ Constellation of the month Super-Skyway Desert Skies: October, 2008 2 Volume LIV, Number 10 Cover Photos: Upper left: The 24-inch telescope is enclosed atop Mount Lemmon within the dome at the left. Lower left: A 24-inch telescope was installed in the newly remodeled dome at the Mount Lemmon Sky Center in April. Right: The 24-inch Mount Lemmon Sky- Center telescope is the one the public uses in programs offered through the UA's College of Science and Steward Observatory. All pho- tos by Adam Block. TAAA Web Page: http://www.tucsonastronomy.org TAAA Phone Number: (520) 792-6414 Office/Position Name Phone E-mail Address President Ken Shaver 762-5094 [email protected] Vice President Keith Schlottman 290-5883 [email protected] Secretary Luke Scott 749-4867 [email protected] Treasurer Terri Lappin 977-1290 [email protected] Member-at-Large George Barber 822-2392 [email protected] Member-at-Large John Kalas 620-6502 [email protected] Member-at-Large Teresa Plymate 883-9113 [email protected] Chief Observer Dr. Mary Turner 586-2244 [email protected] AL Correspondent (ALCor) Nick de Mesa 797-6614 [email protected] Astro-Imaging SIG Steve -

List of Easy Double Stars for Winter and Spring = Easy = Not Too Difficult = Difficult but Possible
List of Easy Double Stars for Winter and Spring = easy = not too difficult = difficult but possible 1. Sigma Cassiopeiae (STF 3049). 23 hr 59.0 min +55 deg 45 min This system is tight but very beautiful. Use a high magnification (150x or more). Primary: 5.2, yellow or white Seconary: 7.2 (3.0″), blue 2. Eta Cassiopeiae (Achird, STF 60). 00 hr 49.1 min +57 deg 49 min This is a multiple system with many stars, but I will restrict myself to the brightest one here. Primary: 3.5, yellow. Secondary: 7.4 (13.2″), purple or brown 3. 65 Piscium (STF 61). 00 hr 49.9 min +27 deg 43 min Primary: 6.3, yellow Secondary: 6.3 (4.1″), yellow 4. Psi-1 Piscium (STF 88). 01 hr 05.7 min +21 deg 28 min This double forms a T-shaped asterism with Psi-2, Psi-3 and Chi Piscium. Psi-1 is the uppermost of the four. Primary: 5.3, yellow or white Secondary: 5.5 (29.7), yellow or white 5. Zeta Piscium (STF 100). 01 hr 13.7 min +07 deg 35 min Primary: 5.2, white or yellow Secondary: 6.3, white or lilac (or blue) 6. Gamma Arietis (Mesarthim, STF 180). 01 hr 53.5 min +19 deg 18 min “The Ram’s Eyes” Primary: 4.5, white Secondary: 4.6 (7.5″), white 7. Lambda Arietis (H 5 12). 01 hr 57.9 min +23 deg 36 min Primary: 4.8, white or yellow Secondary: 6.7 (37.1″), silver-white or blue 8. -
Julian Calendar
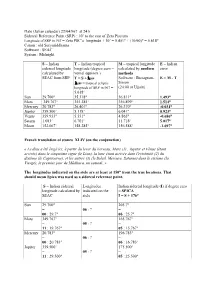
Date (Julian calendar) 22/04/967 at 24 h Sidereal Reference Point (SRP) : 10’ to the east of Zeta Piscium Longitude of SRP in 967 = Zeta PSC’s longitude + 10’ = 5.451° + (10/60)° = 5.618° Canon : old Suryasiddhanta Software : SEAC System : Midnight S = Indian T = Indian tropical M = tropical longitude E = Indian sidereal longitude longitude (degree zero = calculated by modern error calculated by vernal equinox ) methods SEAC from SRP T = S + SRP Software : Bretagnon- E = M - T SRP = tropical ecliptic Simon longitude of SRP in 967 = (24:00 at Ujjain) 5.618° Sun 29.700° 35.318° 36.811° 1.493° Mars 349.767° 355.385° 356.899° 1.514° Mercury 20.783° 26.401° 26.370° -0.031° Jupiter 359.500° 5.118° 6.041° 0.923° Venus 359.933° 5.551° 4.865° -0.686° Saturn 1.083° 6.701° 11.718° 5.017° Moon 152.667° 158.285° 156.588° -1.697° French translation of stanza XLIV (on the conjunction) « Le dieu a été érigé ici, à partir du lever du Verseau, Mars (1) , Jupiter et Vénus (étant arrivés) dans le cinquième signe (le Lion), la lune étant arrivée dans l'extrémité (2) du dixième (le Capricorne), et les autres (3) (le Soleil, Mercure, Saturne) dans le sixième (la Vierge), le premier jour de Mādhava, un samedi. » The longitudes indicated on the stele are at least at 150° from the true locations. That should mean Spica was used as a sidereal reference point. S = Indian sidereal Longitudes Indian sidereal longitude (I) if degree zero longitude calculated by indicated on the = SPICA SEAC stele I = S + 176° Sun 29.700° 205.7° = 06 : ? = 00 : 29.7° 06 : 25.7° Mars 349.767° 165.767° = 05 : ? = 11 : 19.767° 05 : 15.767° Mercury 20.783° 196.783° = 06 : ? = 00 : 20.783° 06 : 16.783° Jupiter 359.500° 175.500° = 05 : ? = 11 : 29.500° 05 : 25.500° Venus 359.933° 175.933° = 05 : ? = 11 : 29.933 05 : 25.933° Saturn 1.083° 177.083° = 06 : ? = 00 : 1.083° 05 : 27.083° (6th sign – 2.917°) Moon 152.667° 328.667° = 10 : ? = 05 : 2.667° 10 : 28.667° (extremity indeed) “Ayanamsa choices There are two main ayanamsas given in the vedic scripture namely Revati-paksha and Chitra- paksha. -

2005 FEBBRAIO Sab Lun Mar Gio 1 Maria Madre Di Dio 17 S
S L P s.p.a. Assicurazioni Spese Legali Peritali e Rischi Accessori Sede e Dir. Gen: 10121 Torino - C.so Matteotti 3 bis - Tel. 011.548.003 - 011.548.748 - Fax 011.548.760 - e-mail: [email protected] SLP Assicurazioni SpA Compagnia Specializzata nel ramo Tutela Giudiziaria Capricorno (Capricornus, Cap) Acquario (Aquarius, Aqr) ALGEDI SADALMELIK M 2 DENEB ALGEDI SADACHBIA DABIH SADALSUUD NASHIRA O ANCHA ALBALI NGC 7009 M 72 SKAT M30 NGC 7293 IL MITO GRECO: IL MITO GRECO: Pan, dio della mitologia greca di carattere infernale ed orgiastico, stava banchettando sull’Olimpo insieme ad altri dei. Improvvisamente Rappresenta Ganimede, il giovane adolescente della cui bellezza si innamorò Zeus, il quale per soddisfare la propria passione amorosa, apparve Tifone, essere mostruoso, mezzo uomo e mezzo belva. Gli Dei, atterriti, fuggirono, trasformandosi in animali: Apollo diventò un assunta la forma di un’aquila, lo rapì e lo trasportò sull’Olimpo. Qui Ganimede, nominato coppiere degli Dei, si occupava personalmente di nibbio, Ermes un ibis, Ares un pesce. Pan (da cui il termine “panico”), terrorizzato, si gettò in un fiume prima di trasformarsi completamnte versare il nettare nella coppa di Zeus. Altre leggende identificano l’Acquario nello stesso Zeus intento a versare l’acqua vitale per la Terra. La in capra e fu così che le sue estremità inferiori assunsero la forma della coda di un pesce. Zeus, stupito e compiaciuto per la metamorfosi, Costellazione era conosciuta anche dagli antichi Babilonesi ed Egizi che nell’Acquario, il Portatore d’Acqua, raffiguravano un uomo che versava decise di collocare in cielo la “capra d’acqua”. -

Astronomical League
Astronomical League 1 Table of Contents Eta Cassiopeiae (U) 3 Kappa Puppis 9 Rho Herculis 15 65 Piscium Zeta Cancri Nu Draconis Psi 1 Piscium Iota Cancri Psi Draconis Zeta Piscium 38 Lyncis 40/41 Draconis Gamma Arietis (U) Alpha Leonis 95 Herculis Lambda Arietis Gamma Leonis (U) 70 Ophiuchi Alpha Piscium 4 54 Leonis 10 Epsilon Lyrae (U) 16 Gamma Andromedae (U) N Hydrae Zeta Lyrae Iota Trianguli Delta Corvi Beta Lyrae Alpha Ursae Minoris 24 Comae Berenices Struve 2404 Gamma Ceti Gamma Virginis Otto Struve 525 Eta Persei 32 Camelopardalis Theta Serpentis Struve 331 5 Alpha Canum Ven. 11 Beta Cygni (U) 17 32 Eridani Zeta Ursae Majoris (U) 57 Aquilae Chi Tauri Kappa Bootis 31 Cygni 1 Camelopardalis Iota Bootis Alpha Capricorni 55 Eridani Pi Bootis Beta Capricorni Beta Orionis Epsilon Bootis Gamma Delphini (U) 118 Tauri 6 Alpha Librae 12 61 Cygni 18 Delta Orionis Xi Bootis Beta Cephei Struve 747 Delta Bootis Struve 2816 Lambda Orionis Mu Bootis Epsilon Pegasi Theta 1 Orionis (U) Delta Serpentis Xi Cephei Iota Orionis Zeta Coronae Borealis Zeta Aquarii Theta 2 Orionis 7 Xi Scorpii 13 Delta Cephei (U) 19 Sigma Orionis Struve 1999 8 Lacertae Zeta Orionis Beta Scorpii (U) 94 Aquarii Gamma Leporis Kappa Herculis Sigma Cassiopeiae Theta Aurigae Nu Scorpii Epsilon Monocerotis Sigma Coronae Borealis Beta Monocerotis (U) 8 16/17 Draconis 14 12 Lyncis Mu Draconis Epsilon Canis Majoris Alpha Herculis Delta Geminorum Delta Herculis 19 Lyncis 36 Ophiuchi Alpha Geminorum Omicron Ophiuchi The 12 stars marked with a (U) are also required for the AL Urban Club. -

SIAC Newsletter April 2015
April 2015 The Sidereal Times Southeastern Iowa Astronomy Club A Member Society of the Astronomical League Club Officers: Minutes March 19, 2015 Executive Committee President Jim Hilkin Vice President Libby published, Bill seconded, ship. Payment can be Vice President Libby Snipes Treasurer Vicki Philabaum Snipes called the meeng and the moon passed. made at a club meeng Secretary David Philabaum Chief Observer David Philabaum to order at 6:33 pm with Vicki gave the Treasurer's or by mailing them to PO Members-at-Large Claus Benninghoven the following members in report stang that the Box 14, West Burlington, Duane Gerling Blake Stumpf aendance: Carl Snipes , current balance in the IA 52655. John moved to Board of Directors Paul Sly, Chuck Block, checking account is approve the Treasurer's Chair Judy Hilkin Vice Chair Ray Reineke Claus Benninghoven, $1,914.04. She also stat- report, seconded by Secretary David Philabaum Members-at-Large Duane Gerling, Bill Stew- ed that she will be send- Chuck, and the moon Frank Libe Blake Stumpf art, Ray Reineke, John ing out noces reminding passed. Dave reported Jim Wilt Toney, and Dave & Vicki people when it is me to that the only groups on Audit Committee Dean Moberg (2012) Philabaum. Lavon Worley renew their member- the schedule at this me JT Stumpf (2013) John Toney (2014) from the conservaon ships. Dues remain $20 are the county Dark Newsletter board was also in aend- per year for a single Wings camps this sum- Karen Johnson ance. John moved to ap- membership and $30 per mer. Libby reported that -

Astronomy Notes · • 17 Jane's Corner ••.• • • 33 the Technical Side •
r th f IIIiI I l1li I P'AN-KU, the legendary. son of CHAOS and architect of the Chinese universe creating the world, assisted by the Dragon, Tiger, Bird, and Tortoise. Vo I m Ispe Spring u er 1 Advantageo on membeMlup in -the In-tvr..nationai SocJ..uy on Planua.tUmn Educ,a):OM Mn be nJteely 0 b-taA.,ned by wJtLt[ng -to: Mr. Walter Tenschert Thomas Jefferson High School 6560 Braddock Road Alexandria, VA 22312 * * * * * * * * * * * CONTENTS Checklist of Planetary Configurations THE PLANETARIAN is published each March, for 1975 June, September, and December by the Robert C. Victor 4 International Society of Planetarium Planetarium for the Deaf Educators, Inc., under the auspices of Lionel Daniel . • • 7 the Publications Committee. The Third Stage of Planetarium Evolution Max L. Ary . • . • • • 11 To make a change of address, please an The Stars of Primeval China old mailing label, along with the new Julius D.W. Staal 20 address, to: Ronald N. Hartman Planetariums on Parade . 33 Mt. San Antonio College Celestial Navigation Planetarium Harry E. Crull •...•• · • 35 Walnut The History of the Planetarium California 91789 Charles F. Hagar ..••.•••• 42 Please allow 30 days for an address Construction of the Budapest Planetarium change to take effect. Gyula Schalk . • .... • • . 48 Some Thoughts on Planetarium Show Music Tim Clark . • 51 Music in OMSI's Harry C. Kendall EDITOR: Frank Jettner Planetarium Circulation Director: Ron Hartman Dwight Gruber • • 52 Feature Editors: Von Del Chamberlain, Popular Music and Slides in the M. Chartrand, L. DeVries, T. Gates, Planetarium J. Geoghegan, O.R. Norton, G. -

November 2020 BRAS Newsletter
A Mars efter Lowell's Glober ca. 1905-1909”, from Percival Lowell’s maps; National Maritime Museum, Greenwich, London (see Page 6) Monthly Meeting November 9th at 7:00 PM, via Jitsi (Monthly meetings are on 2nd Mondays at Highland Road Park Observatory, temporarily during quarantine at meet.jit.si/BRASMeets). GUEST SPEAKER: Chuck Allen from the Astronomical League will speak about The Cosmic Distance Ladder, which explores the historical advancement of distance determinations in astronomy. What's In This Issue? President’s Message Member Meeting Minutes Business Meeting Minutes Outreach Report Asteroid and Comet News Light Pollution Committee Report Globe at Night Member’s Corner – John Nagle ALPO 2020 Conference Astro-Photos by BRAS Members - MARS Messages from the HRPO REMOTE DISCUSSION Solar Viewing Edge of Night Natural Sky Conference Recent Entries in the BRAS Forum Observing Notes: Pisces – The Fishes Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society BRAS YouTube Channel Baton Rouge Astronomical Society Newsletter, Night Visions Page 2 of 24 November 2020 President’s Message Welcome to the home stretch for 2020. The nights are starting earlier and earlier as the weather becomes more and more comfortable and all of our old favorites of the fall and winter skies really start finding their places right where they belong. October was a busy month for us, with several big functions at the Observatory, including two oppositions and two more all night celebrations. By comparison, November is looking fairly calm, the big focus there is going to be our third annual Natural Sky Conference on the 13th, which I’m encouraging people who care about the state of light pollution in our city and the surrounding area to get involved in. -

Planetary Post March 2017
ISSUE # 118 Planetary Post March 2017 As is known, March is a “light” month since BRAS’ annual star party draws ASTRONEWS personnel away from HRPO for a week. Patrons will hardly notice—the first attempt of the year to view the most elusive planet, Mercury, is this month; Dr. Michoud Assembly Facility Struck Juhan Frank gives an outline of star birth and death to prepare the public for by Tornado <> Uranus Distances the upcoming presentation of information about Tabby’s Star; our latest twilight Itself from Zeta Piscium <> Jupiter viewing session is scheduled; and Dr. Juana Moreno and her students return Enters Evening Sky <> with their annual nanotechnology event, suitable for most ages of the family. Penumbral Lunar Eclipse Views One more surprise—the Skygazing Tip section will return in April with all new Hindered by Clouds <> general suggestions and a suggested object to view! Attendance for HRPO Solar Viewing Doubles in 2017 <> Geomagnetic Storm Activity Calendar of events Predicted for Early March <> 30th Anniversary of Supernova 1987A Discovery <> TRAPPIST1 has HRPO will be closed on 22, 23 and 24 March for the Hodges Gardens Multiple Planets Orbiting Star Party. FRIDAY NIGHT LECTURE SERIES No admission fee. For ages fourteen and older. Fridays at 7:30pm 3 March: “Stellar Evolution” A star’s life is very dependent on its initial mass. The unaidedeye stars that we see nightly are at different stages in their development. Some are young and blue, some middleaged and yellow, some elderly and red. LSU physics professor Juhan Frank will condense the lives of stars to one hour! 20/20 VISION CAMPAIGN 17 March: “Mercury and Venus” One zips around the Sun in eightyeight Earth days and one has a hellish atmosphere of temperature and pressure. -

Reflectionsreflections the Newsletter of the Popular Astronomy Club ESTABLISHED 1936 February 2021
Affiliated with ReflectionsReflections The Newsletter of the Popular Astronomy Club ESTABLISHED 1936 February 2021 President’s Corner February 2021 the speed of light, this means the object is Welcome to the Febru- trapped in the black hole. ary edition of Reflec- The escape velocity for a planet is the speed at tions. We are in the which an object (like a rocket) would have to middle of winter, which be launched from the surface of the planet so should be obvious to that it would fly up and completely escape Page Topic everyone and especially from the planet and never fall back down for astronomers. We again. A rocket could orbit a planet at a slightly 1-2 Presidents have had very few op- slower speed and never fall back to the Corner Alan Sheidler portunities to view ce- planet’s surface, but in that case, the rocket 2-4 Announcements lestial objects and when would not have escaped, it would have been 5-10 Contributions we have, it has been too cold or snowy for trapped in an orbit around the planet. 11 Astronomy in most of us to get out under the stars. Print We can calculate the escape velocity for the For many of us, this is a time when we take a 12-13 Skyward Earth and other solar system objects using the vacation from observing and do other things 14 Upcoming Events fairly simple equation below. For those of you (like buy new telescopes or plan observing 15 Sign-Up Sheet not wanting to bother doing the math, I creat- sessions when the weather improves this 16 Astronomical ed the following table showing the escape ve- spring). -

Instruction Manual
iOptron® GEM28 German Equatorial Mount Instruction Manual Product GEM28 and GEM28EC Read the included Quick Setup Guide (QSG) BEFORE taking the mount out of the case! This product is a precision instrument and uses a magnetic gear meshing mechanism. Please read the included QSG before assembling the mount. Please read the entire Instruction Manual before operating the mount. You must hold the mount firmly when disengaging or adjusting the gear switches. Otherwise personal injury and/or equipment damage may occur. Any worm system damage due to improper gear meshing/slippage will not be covered by iOptron’s limited warranty. If you have any questions please contact us at [email protected] WARNING! NEVER USE A TELESCOPE TO LOOK AT THE SUN WITHOUT A PROPER FILTER! Looking at or near the Sun will cause instant and irreversible damage to your eye. Children should always have adult supervision while observing. 2 Table of Content Table of Content ................................................................................................................................................. 3 1. GEM28 Overview .......................................................................................................................................... 5 2. GEM28 Terms ................................................................................................................................................ 6 2.1. Parts List ................................................................................................................................................. -

RET 36 Cover +
Revue d’Etudes Tibétaines numéro trente-six — Octobre 2016 Revue d’Etudes Tibétaines numéro trente-six — Octobre 2016 ISSN 1768-2959 Directeur : Jean-Luc Achard. Comité de rédaction : Alice Travers, Jean-Luc Achard. Comité de lecture : Ester Bianchi (Università degli Studi di Perugia), Fabienne Jagou (EFEO), Rob Mayer (Oriental Institute, University of Oxford), Fernand Meyer (CNRS-EPHE), Françoise Pommaret (CNRS), Ramon Prats (Universitat Pompeu Fabra, Barcelona), Charles Ramble (EPHE, CNRS), Françoise Robin (INALCO), Brigitte Steinman (Université de Lille), Alice Travers (CNRS), Jean-Luc Achard (CNRS). Périodicité La périodicité de la Revue d’Etudes Tibétaines est généralement bi-annuelle, les mois de parution étant, sauf indication contraire, Octobre et Avril. Les contributions doivent parvenir au moins six (6) mois à l’avance. Les dates de proposition d’articles au comité de lecture sont Novembre pour une parution en Avril, et Mai pour une parution en Octobre. Participation La participation est ouverte aux membres statutaires des équipes CNRS, à leurs membres associés, aux doctorants et aux chercheurs non-affiliés. Les articles et autres contributions sont proposées aux membres du comité de lecture et sont soumis à l’approbation des membres du comité de rédaction. Les articles et autres contributions doivent être inédits ou leur ré- édition doit être justifiée et soumise à l’approbation des membres du comité de lecture. Les documents doivent parvenir sous la forme de fichiers Word, envoyés à l’adresse du directeur ([email protected]). Comptes-rendus Contacter le directeur de publication, à l’adresse électronique suivante : [email protected] Langues Les langues acceptées dans la revue sont le français (en priorité), l’anglais, l’allemand, l’italien, l’espagnol, le tibétain et le chinois.