DOCSLIB.ORG

Classifying Chemical Elements and Particles: from the Atomic to the Sub-Atomic World Maurice Kibler

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Classifying Chemical Elements and Particles: from the Atomic to the Sub-Atomic World Maurice Kibler Classifying chemical elements and particles: from the atomic to the sub-atomic world Maurice Kibler To cite this version: Maurice Kibler. Classifying chemical elements and particles: from the atomic to the sub-atomic world. Second Harry Wiener International Memorial Conference, Jul 2003, Banff, Canada. pp.297-329. hal- 00000783v2 HAL Id: hal-00000783 https://hal.archives-ouvertes.fr/hal-00000783v2 Submitted on 8 Jan 2008 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. http://arXiv.org/quant-ph/0310155 October 2003 Classifying chemical elements and particles: from the atomic to the sub-atomic world Maurice R Kibler Institut de Physique Nucléaire IN2P3-CNRS et Université Claude Bernard Lyon-1 43, Boulevard du 11 Novembre 1918 69622 Villeurbanne Cedex, France Abstract This paper presents two facets. First, we show that the periodic table of chemical elements can be described, understood and modified (as far as its format is concerned) on the basis of group theory and more specifically by using the group SO(4,2)xSU(2). Second, we show that “periodic tables” also exist in the sub- atomic and sub-nuclear worlds and that group theory is of paramount importance for these tables. In that sense, this paper may be considered as an excursion, for non specialists, into nuclear and particle physics. The present work was presented as an invited talk to The Second Harry Wiener International Memorial Conference: “ The Periodic Table: Into the 21 st Century ”, Brewster’s KGR near Banff, Alberta, Canada, July 14-20, 2003. In memory of Jean Gréa This paper is dedicated to the memory of Jean Gréa who, like Harry Wiener, was a universal man. Jean was a physicist with a large flow of activities in theoretical physics. He started with nuclear physics, then switched to pre-quantum mechanics (theory of hidden variables), continued with simulations in physics and the theory of signal and finally made important contributions in didactics and philosophy of sciences. He was the co-founder of the LIRDHIST ( Laboratoire Interdisciplinaire de Recherche en Didactique et en Histoire des Sciences et Techniques ) at the Université Claude Bernard Lyon 1 . As a teacher, he knew how to communicate his enthusiasm to students. He was very much oriented to other people. He knew how to listen to others, how to answer questions by sometimes asking other questions and how to help people. Merci Jean. Published in: The Periodic Table: Into the 21 st Century , D.H. Rouvray and R.B. King, Eds., Research Studies Press, Baldock, United Kingdom, 2004, pp. 297-329. Classifying chemical elements and particles: from the atomic to the sub-atomic world.........................................................................................................................1 1 Introduction ......................................................................................................3 2 Elements from Antiquity to 2003 .....................................................................4 2.1 From Antiquity to the 18 th century ...........................................................4 2.2 From Lavoisier to Mendeleev...................................................................5 2.3 From 1870 to 2003....................................................................................7 2.4 Comparison with particle physics.............................................................7 3 Group theory in Chemistry and Physics ...........................................................9 3.1 Groups ......................................................................................................9 3.2 Representations.......................................................................................10 3.3 Examples ................................................................................................11 3.3.1 The group SO(4).................................................................................11 3.3.2 The group SU(3).................................................................................11 3.3.3 The group SO(4,2)..............................................................................11 4 Group theory and the periodic table of chemical elements.............................12 4.1 The importance of the atomic number Z.................................................12 4.2 The importance of quantum mechanics..................................................12 4.3 The Madelung rule..................................................................................13 4.4 An SO(4,2)xSU(2) approach to the periodic table..................................15 4.5 Towards a quantitative approach............................................................18 5 A periodic table in the sub-atomic word.........................................................19 5.1 The use of group theory for particles and their interactions ...................19 5.2 The standard model.................................................................................19 5.3 How has the periodic table of particles arisen?.......................................20 5.3.1 1932: The ideal world (the Golden Age) ............................................20 5.3.2 1962: The world gets complicated......................................................21 5.3.3 1964: The world gets simpler .............................................................23 5.3.4 Other important steps..........................................................................25 5.4 Some current pivotal research in particle physics...................................26 5.4.1 Theoretical aspects..............................................................................26 5.4.2 Experimental aspects ..........................................................................27 6 Closing remarks..............................................................................................28 Acknowledgments ..................................................................................................29 Elements of bibliography........................................................................................29 Some primary sources on the periodic system....................................................29 Historical outlines...............................................................................................29 Periodic table in Flatland....................................................................................30 Periodic table for molecules ...............................................................................30 Quantum-mechanical approaches to the periodic table ......................................30 SO(4,2) approaches to the periodic table............................................................30 Other group theoretical approaches to the periodic table ...................................31 Ceric and yttric rare earths..................................................................................31 New meson and new baryon...............................................................................31 2 Classifying chemical elements and particles: from the atomic to the sub-atomic world Maurice R Kibler Institut de Physique Nucléaire IN2P3-CNRS et Université Claude Bernard Lyon-1 43, Boulevard du 11 Novembre 1918 69622 Villeurbanne Cedex, France 1 Introduction Holding a conference in 2003 on the periodic table of chemical elements may seem somewhat curious at first sight. The periodic table has been the object of so many studies that it is hard to imagine any new developments on the subject except perhaps from the perspective of History, Scientific Philosophy, Epistemology, Sociology or Politics. From the point of view of Chemistry and Physics, what can be said about the periodic table in the 21 st century? Along this vein, we may ask the following questions. • Does the periodic table have a limit? • Do other formats in two or three dimensions provide insight for teaching purposes? • What can be learned from periodic tables in other dimensions (as for example in Flatland, a two-dimensional space, or in a four-dimensional space)? • What can be gained from a quantum-mechanical approach and what is the importance of relativistic quantum mechanics for the periodic table? • What can be gained from a group theoretical approach to the periodic table? • What are the implications of a group theoretical approach for molecules? • How may the periodic table of neutral atoms be extended to a periodic table for ions or to a periodic table for molecules? • What are the analogues of the periodic table in the sub-atomic world and in the sub-nuclear world? Many of these questions were addressed during the Second Harry Wiener International Memorial Conference and the reader will find some answers in this volume and in the other publications connected to the conference. This paper deals with two of the preceding questions. First, we show that the periodic table of chemical elements can be described, understood and modified (as far as its format is concerned) on the basis of group theory and more specifically
Load more

Recommended publications
  • LHC Explore Pentaquark
    LHC Explore Pentaquark Scientists at the Large Hadron Collider have announced the discovery of a new particle called the pentaquark. [9] CERN scientists just completed one of the most exciting upgrades on the Large Hadron Collider—the Di-Jet Calorimeter (DCal). [8] As physicists were testing the repairs of LHC by zipping a few spare protons around the 17 mile loop, the CMS detector picked up something unusual. The team feverishly pored over the data, and ultimately came to an unlikely conclusion—in their tests, they had accidentally created a rainbow universe. [7] The universe may have existed forever, according to a new model that applies quantum correction terms to complement Einstein's theory of general relativity. The model may also account for dark matter and dark energy, resolving multiple problems at once. [6] This paper explains the Accelerating Universe, the Special and General Relativity from the observed effects of the accelerating electrons, causing naturally the experienced changes of the electric field potential along the moving electric charges. The accelerating electrons explain not only the Maxwell Equations and the Special Relativity, but the Heisenberg Uncertainty Relation, the wave particle duality and the electron’s spin also, building the bridge between the Classical and Relativistic Quantum Theories. The Big Bang caused acceleration created the radial currents of the matter and since the matter composed of negative and positive charges, these currents are creating magnetic field and attracting forces between the parallel moving electric currents. This is the gravitational force experienced by the matter, and also the mass is result of the electromagnetic forces between the charged particles.
    [Show full text]
  • Pentaquark Search Shows How Science Moves Forward
    Although initial results were encouraging, physicists searching for an exotic five-quark particle now think it probably doesn’t exist. The debate over the pentaquark search shows how science moves forward. The rise and fall of the PE NTAQUAR K by Kandice Carter, Jefferson Lab 16 Three years ago, research teams around the stars are made. Yet he and his peers had no world announced they had found data hinting at means to verify its existence. the existence of an exotic particle containing Luminaries of 16th-19th century physics, five quarks, more than ever observed in any other including Newton, Fresnel, Stokes, and Maxwell, quark-composite particle. More than two dozen debated at length the properties of their physi- experiments have since taken aim at the particle, cal version of the philosophical concept, which dubbed the pentaquark, and its possible partners, they called ether. in the quest to turn a hint into a discovery. It’s a The ether was a way to explain how light scenario that often plays out in science: an early could travel through empty space. In 1881, theory or observation points to a potentially Albert A. Michelson began to explore the ether important discovery, and experimenters race to concept with experimental tools. But his first corroborate or to refute the idea. experiments, which seemed to rule out the “Research is the process of going up alleys to existence of the ether, were later realized to be see if they are blind,” said Marston Bates, a zool- inconclusive. ogist whose research on mosquitoes led to Six years later, Michelson paired up with an understanding of how yellow fever is spread.
    [Show full text]
  • The Pev-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability
    The PeV-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability Waqas Ahmed ? 1, Adeel Mansha ? 2, Tianjun Li ? ~ 3, Shabbar Raza ∗ 4, Joydeep Roy ? 5, Fang-Zhou Xu ? 6, ? CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, P. R. China ~School of Physical Sciences, University of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing 100049, P. R. China ∗ Department of Physics, Federal Urdu University of Arts, Science and Technology, Karachi 75300, Pakistan Institute of Modern Physics, Tsinghua University, Beijing 100084, China Abstract The null results of the LHC searches have put strong bounds on new physics scenario such as supersymmetry (SUSY). With the latest values of top quark mass and strong coupling, we study the upper bounds on the sfermion masses in Split-SUSY from the observed Higgs boson mass and electroweak (EW) vacuum stability. To be consistent with the observed Higgs mass, we find that the largest value of supersymmetry breaking 3 1:5 scales MS for tan β = 2 and tan β = 4 are O(10 TeV) and O(10 TeV) respectively, thus putting an upper bound on the sfermion masses around 103 TeV. In addition, the Higgs quartic coupling becomes negative at much lower scale than the Standard Model (SM), and we extract the upper bound of O(104 TeV) on the sfermion masses from EW vacuum stability. Therefore, we obtain the PeV-Scale Split-SUSY. The key point is the extra contributions to the Renormalization Group Equation (RGE) running from arXiv:1901.05278v1 [hep-ph] 16 Jan 2019 the couplings among Higgs boson, Higgsinos, and gauginos.
    [Show full text]
  • Wimps and Machos ENCYCLOPEDIA of ASTRONOMY and ASTROPHYSICS
    WIMPs and MACHOs ENCYCLOPEDIA OF ASTRONOMY AND ASTROPHYSICS WIMPs and MACHOs objects that could be the dark matter and still escape detection. For example, if the Galactic halo were filled –3 . WIMP is an acronym for weakly interacting massive par- with Jupiter mass objects (10 Mo) they would not have ticle and MACHO is an acronym for massive (astrophys- been detected by emission or absorption of light. Brown . ical) compact halo object. WIMPs and MACHOs are two dwarf stars with masses below 0.08Mo or the black hole of the most popular DARK MATTER candidates. They repre- remnants of an early generation of stars would be simi- sent two very different but reasonable possibilities of larly invisible. Thus these objects are examples of what the dominant component of the universe may be. MACHOs. Other examples of this class of dark matter It is well established that somewhere between 90% candidates include primordial black holes created during and 99% of the material in the universe is in some as yet the big bang, neutron stars, white dwarf stars and vari- undiscovered form. This material is the gravitational ous exotic stable configurations of quantum fields, such glue that holds together galaxies and clusters of galaxies as non-topological solitons. and plays an important role in the history and fate of the An important difference between WIMPs and universe. Yet this material has not been directly detected. MACHOs is that WIMPs are non-baryonic and Since extensive searches have been done, this means that MACHOS are typically (but not always) formed from this mysterious material must not emit or absorb appre- baryonic material.
    [Show full text]
  • B2.IV Nuclear and Particle Physics
    B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ......................
    [Show full text]
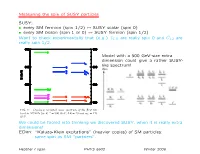
  • Measuring the Spin of SUSY Particles SUSY: • Every SM Fermion (Spin 1/2
    Measuring the spin of SUSY particles SUSY: • every SM fermion (spin 1/2) ↔ SUSY scalar (spin 0) • every SM boson (spin 1 or 0) ↔ SUSY fermion (spin 1/2) Want to check experimentally that (e.g.) eL,R are really spin 0 and Ce1,2 are really spin 1/2. 2 preserve the 5th dimensional momentum (KK number). The corresponding coupling constants among KK modes Model with a 500 GeV-size extra are simply equal to the SM couplings (up to normaliza- tion factors such as √2). The Feynman rules for the KK dimension could give a rather SUSY- modes can easily be derived (e.g., see Ref. [8, 9]). like spectrum! In contrast, the coefficients of the boundary terms are not fixed by Standard Model couplings and correspond to new free parameters. In fact, they are renormalized by the bulk interactions and hence are scale dependent [10, 11]. One might worry that this implies that all pre- dictive power is lost. However, since the wave functions of Standard Model fields and KK modes are spread out over the extra dimension and the new couplings only exist on the boundaries, their effects are volume sup- pressed. We can get an estimate for the size of these volume suppressed corrections with naive dimensional analysis by assuming strong coupling at the cut-off. The FIG. 1: One-loop corrected mass spectrum of the first KK −1 result is that the mass shifts to KK modes from bound- level in MUEDs for R = 500 GeV, ΛR = 20 and mh = 120 ary terms are numerically equal to corrections from loops GeV.
    [Show full text]
  • MASTER THESIS Linking the B-Physics Anomalies and Muon G
    MSc PHYSICS AND ASTRONOMY GRAVITATION, ASTRO-, AND PARTICLE PHYSICS MASTER THESIS Linking the B-physics Anomalies and Muon g − 2 A Phenomenological Study Beyond the Standard Model By Anders Rehult 12623881 February - October 2020 60 EC Supervisor/Examiner: Second Examiner: prof. dr. Robert Fleischer prof. dr. Piet Mulders i Abstract The search for physics beyond the Standard Model is guided by anomalies: discrepancies between the theoretical predictions and experimental measurements of physical quantities. Hints of new physics are found in the recently observed B-physics anomalies and the long-standing anomalous magnetic dipole moment of the muon, muon g − 2. The former include a group of anomalous measurements related to the quark-level transition b ! s. We investigate what features are required of a theory to explain these b ! s anomalies simultaneously with muon g − 2. We then consider three kinds of models that might explain the anomalies: models with leptoquarks, hypothetical particles that couple leptons to quarks; Z0 models, which contain an additional fundamental force and a corresponding force carrier; and supersymmetric scenarios that postulate a symmetry that gives rise to a partner for each SM particle. We identify a leptoquark model that carries the necessary features to explain both kinds of anomalies. Within this model, we study the behaviour of 0 muon g − 2 and the anomalous branching ratio of Bs mesons, bound states of b and s quarks, into muons. 0 ¯0 0 ¯0 The Bs meson can spontaneously oscillate into its antiparticle Bs , a phenomenon known as Bs −Bs mixing. We calculate the effects of this mixing on the anomalous branching ratio.
    [Show full text]
  • Introduction to Subatomic- Particle Spectrometers∗
    IIT-CAPP-15/2 Introduction to Subatomic- Particle Spectrometers∗ Daniel M. Kaplan Illinois Institute of Technology Chicago, IL 60616 Charles E. Lane Drexel University Philadelphia, PA 19104 Kenneth S. Nelsony University of Virginia Charlottesville, VA 22901 Abstract An introductory review, suitable for the beginning student of high-energy physics or professionals from other fields who may desire familiarity with subatomic-particle detection techniques. Subatomic-particle fundamentals and the basics of particle in- teractions with matter are summarized, after which we review particle detectors. We conclude with three examples that illustrate the variety of subatomic-particle spectrom- eters and exemplify the combined use of several detection techniques to characterize interaction events more-or-less completely. arXiv:physics/9805026v3 [physics.ins-det] 17 Jul 2015 ∗To appear in the Wiley Encyclopedia of Electrical and Electronics Engineering. yNow at Johns Hopkins University Applied Physics Laboratory, Laurel, MD 20723. 1 Contents 1 Introduction 5 2 Overview of Subatomic Particles 5 2.1 Leptons, Hadrons, Gauge and Higgs Bosons . 5 2.2 Neutrinos . 6 2.3 Quarks . 8 3 Overview of Particle Detection 9 3.1 Position Measurement: Hodoscopes and Telescopes . 9 3.2 Momentum and Energy Measurement . 9 3.2.1 Magnetic Spectrometry . 9 3.2.2 Calorimeters . 10 3.3 Particle Identification . 10 3.3.1 Calorimetric Electron (and Photon) Identification . 10 3.3.2 Muon Identification . 11 3.3.3 Time of Flight and Ionization . 11 3.3.4 Cherenkov Detectors . 11 3.3.5 Transition-Radiation Detectors . 12 3.4 Neutrino Detection . 12 3.4.1 Reactor Neutrinos . 12 3.4.2 Detection of High Energy Neutrinos .
    [Show full text]
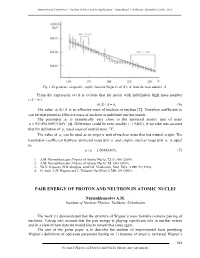
  • Pair Energy of Proton and Neutron in Atomic Nuclei
    International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again.
    [Show full text]
  • Structure of Matter
    STRUCTURE OF MATTER Discoveries and Mysteries Part 2 Rolf Landua CERN Particles Fields Electromagnetic Weak Strong 1895 - e Brownian Radio- 190 Photon motion activity 1 1905 0 Atom 191 Special relativity 0 Nucleus Quantum mechanics 192 p+ Wave / particle 0 Fermions / Bosons 193 Spin + n Fermi Beta- e Yukawa Antimatter Decay 0 π 194 μ - exchange 0 π 195 P, C, CP τ- QED violation p- 0 Particle zoo 196 νe W bosons Higgs 2 0 u d s EW unification νμ 197 GUT QCD c Colour 1975 0 τ- STANDARD MODEL SUSY 198 b ντ Superstrings g 0 W Z 199 3 generations 0 t 2000 ν mass 201 0 WEAK INTERACTION p n Electron (“Beta”) Z Z+1 Henri Becquerel (1900): Beta-radiation = electrons Two-body reaction? But electron energy/momentum is continuous: two-body two-body momentum energy W. Pauli (1930) postulate: - there is a third particle involved + + - neutral - very small or zero mass p n e 휈 - “Neutrino” (Fermi) FERMI THEORY (1934) p n Point-like interaction e 휈 Enrico Fermi W = Overlap of the four wave functions x Universal constant G -5 2 G ~ 10 / M p = “Fermi constant” FERMI: PREDICTION ABOUT NEUTRINO INTERACTIONS p n E = 1 MeV: σ = 10-43 cm2 휈 e (Range: 1020 cm ~ 100 l.yr) time Reines, Cowan (1956): Neutrino ‘beam’ from reactor Reactions prove existence of neutrinos and then ….. THE PREDICTION FAILED !! σ ‘Unitarity limit’ > 100 % probability E2 ~ 300 GeV GLASGOW REFORMULATES FERMI THEORY (1958) p n S. Glashow W(eak) boson Very short range interaction e 휈 If mass of W boson ~ 100 GeV : theory o.k.
    [Show full text]
  • Electroweak Radiative B-Decays As a Test of the Standard Model and Beyond Andrey Tayduganov
    Electroweak radiative B-decays as a test of the Standard Model and beyond Andrey Tayduganov To cite this version: Andrey Tayduganov. Electroweak radiative B-decays as a test of the Standard Model and beyond. Other [cond-mat.other]. Université Paris Sud - Paris XI, 2011. English. NNT : 2011PA112195. tel-00648217 HAL Id: tel-00648217 https://tel.archives-ouvertes.fr/tel-00648217 Submitted on 5 Dec 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. LAL 11-181 LPT 11-69 THESE` DE DOCTORAT Pr´esent´eepour obtenir le grade de Docteur `esSciences de l’Universit´eParis-Sud 11 Sp´ecialit´e:PHYSIQUE THEORIQUE´ par Andrey Tayduganov D´esint´egrationsradiatives faibles de m´esons B comme un test du Mod`eleStandard et au-del`a Electroweak radiative B-decays as a test of the Standard Model and beyond Soutenue le 5 octobre 2011 devant le jury compos´ede: Dr. J. Charles Examinateur Prof. A. Deandrea Rapporteur Prof. U. Ellwanger Pr´esident du jury Prof. S. Fajfer Examinateur Prof. T. Gershon Rapporteur Dr. E. Kou Directeur de th`ese Dr. A. Le Yaouanc Directeur de th`ese Dr.
    [Show full text]
  • Basic Ideas of the Standard Model
    BASIC IDEAS OF THE STANDARD MODEL V.I. ZAKHAROV Randall Laboratory of Physics University of Michigan, Ann Arbor, Michigan 48109, USA Abstract This is a series of four lectures on the Standard Model. The role of conserved currents is emphasized. Both degeneracy of states and the Goldstone mode are discussed as realization of current conservation. Remarks on strongly interact- ing Higgs fields are included. No originality is intended and no references are given for this reason. These lectures can serve only as a material supplemental to standard textbooks. PRELIMINARIES Standard Model (SM) of electroweak interactions describes, as is well known, a huge amount of exper- imental data. Comparison with experiment is not, however, the aspect of the SM which is emphasized in present lectures. Rather we treat SM as a field theory and concentrate on basic ideas underlying this field theory. Th Standard Model describes interactions of fields of various spins and includes spin-1, spin-1/2 and spin-0 particles. Spin-1 particles are observed as gauge bosons of electroweak interactions. Spin- 1/2 particles are represented by quarks and leptons. And spin-0, or Higgs particles have not yet been observed although, as we shall discuss later, we can say that scalar particles are in fact longitudinal components of the vector bosons. Interaction of the vector bosons can be consistently described only if it is highly symmetrical, or universal. Moreover, from experiment we know that the corresponding couplings are weak and can be treated perturbatively. Interaction of spin-1/2 and spin-0 particles are fixed by theory to a much lesser degree and bring in many parameters of the SM.
    [Show full text]