DOCSLIB.ORG

Experimental Apparatus for Quantum Pumping with a Bose-Einstein Condensate." (2016)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Experimental Apparatus for Quantum Pumping with a Bose-Einstein Condensate. W&M ScholarWorks Dissertations, Theses, and Masters Projects Theses, Dissertations, & Master Projects 2016 Experimental Apparatus for Quantum Pumping with a Bose- Einstein Condensate. Megan K. Ivory College of William and Mary Follow this and additional works at: https://scholarworks.wm.edu/etd Part of the Physics Commons Recommended Citation Ivory, Megan K., "Experimental Apparatus for Quantum Pumping with a Bose-Einstein Condensate." (2016). Dissertations, Theses, and Masters Projects. Paper 1593092109. https://dx.doi.org/doi:10.21220/m2-4bwj-8856 This Dissertation is brought to you for free and open access by the Theses, Dissertations, & Master Projects at W&M ScholarWorks. It has been accepted for inclusion in Dissertations, Theses, and Masters Projects by an authorized administrator of W&M ScholarWorks. For more information, please contact [email protected]. Experimental Apparatus for Quantum Pumping with a Bose-Einstein Condensate Megan K. Ivory Sidman, Pennsylvania Master of Science, College of William and Mary, 2009 Bachelor of Science, Saint Vincent College, 2007 A Dissertation presented to the Graduate Faculty of the College of William and Mary in Candidacy for the Degree of Doctor of Philosophy Department of Physics The College of William and Mary January 2016 ©2015 Megan K. Ivory All rights reserved. APPROVAL PAGE This Dissertation is submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy Approved by the Committee, September, 2015 Committee Chair Associate Professor Seth Aubin, Physics The (College of William and Mary Professor John B. Delos, Physics The College of William and Mary Associa^'Prcfessor Irina Novikova, Physics The College crf’William and Mary Professor Wftfiam Cooke,ook^plfysTC Physics The College of William and Mary A Professor Kunal Das, Physics Kutztown University ABSTRACT Quantum pumping is a method of transporting particles through a circuit without an external applied voltage or chemical potential, but instead with localized time-varying potentials. Ballistic quantum pumping has been theorized in mesoscopic solid state sys­ tems, but experimental verifications have been challenging due to the capacitive coupling and rectification inherent to electronic systems. Using ultracold neutral atoms to test and verify the theoretical predictions of quantum pumping reduces these challenges while providing the advantages of easy confinement and manipulation, a high degree of coher­ ence, and bosons as well as fermions. In addition, ultracold atoms allow smooth tunability between classical thermal gases and quantum gases. Here, we design, build, characterize, and optimize a dual-species experimental apparatus capable of quantum pumping exper­ iments with Bose-Einstein condensates on an atom chip. We produce quasi-pure 87Rb Bose-Einstein condensates of ~ 104 atoms and successfully laser-cool 39K. We lay the experimental groundwork for quantum pumping experiments with ultracold atoms and characterize the classical dynamics of the system. These classical dynamics are supported with theoretical modeling that we have developed to compare the dramatic differences between the classical and quantum results of a double barrier turnstile pump as well as its single barrier building blocks. TABLE OF CONTENTS Acknowledgments.................................................................................................................... v Dedication ................................................................................................................................ vii List of Tables ..............................................................................................................................viii List of Figures ....................................................................................................................... ix CHAPTER 1 Introduction ................................................................................................................ 1 1.1 Background and history ................................................................................. 3 1.2 A pplications ....................................................................................................... 5 1.3 Structure of the thesis .................................................................................... 7 2 Ultracold atom theory ............................................................................................. 9 2.1 Introduction ....................................................................................................... 9 2.2 Magneto-optical trapping ................................................................................. 11 2.2.1 Laser cooling ........................................................................................ 12 2.2.2 Spatial confinement with a magnetic field ........................................ 15 2.3 Optical molasses ................................................................................................. 16 2.4 Magnetic trapping .............................................................................................. 17 2.4.1 Optical p u m p in g .................................................................................. 19 2.4.2 Magnetic tra n s p o rt .............................................................................. 20 2.5 Atom chip tra p p in g ........................................................................................... 21 2.6 Evaporative cooling ........................................................................................... 24 2.7 Bose-Einstein condensate ................................................................................. 26 i 2.8 Im a g in g ............................................................................................................ 30 2.8.1 Absorption im aging .............................................................................. 31 2.8.2 Fluorescence imaging .......................................................................... 32 2.9 Temperature m easurem ent ............................................................................ 33 3 Optical dipole traps ................................................................................................... 36 3.1 Introduction ...................................................................................................... 36 3.2 Two-level atom theory for a dipole tr a p ....................................................... 37 3.3 Calculating dipole trap potentials ............................................................... 40 3.3.1 Calculating the frequency of oscillation .......................................... 42 3.4 Optical l a t t ic e s ............................................................................................... 43 4 Experimental apparatus ......................................................................................... 47 4.1 Lab la y o u t ......................................................................................................... 49 4.2 Vacuum s y s te m ............................................................................................... 51 4.3 Laser system and locks ................................................................................... 52 4.3.1 Rubidium laser s y s te m ...................................................................... 55 4.3.2 Potassium laser system ...................................................................... 59 4.3.3 Tapered amplifiers .............................................................................. 60 4.4 Experimental procedure ............................................................................... 62 4.4.1 Magneto-optical trap and molasses ................................................. 62 4.4.2 Optical pumping, magnetic trapping, and transport .................... 67 4.4.3 Chip t r a p.............................................................................................. 70 4.4.4 Dipole trapping at the atom c h ip .................................................... 71 4.5 Imaging system s ............................................................................................... 75 5 Production of Bose-Einstein condensates .............................................................. 79 5.1 Evaporative cooling ......................................................................................... 80 ii 5.2 Dimple t r a p ...................................................................................................... 84 5.3 Bose-Einstein condensate ................................................................................ 87 5.4 Image analysis ................................................................................................... 89 5.5 Conclusion ......................................................................................................... 92 6 Classical aspects of quantum pumping ................................................................ 94 6.1 Introduction ...................................................................................................... 94 6.2 M o d e l ................................................................................................................ 97 6.2.1 Scaled u n i t s ...............................................................................................100 6.2.2 M eth o d s ....................................................................................................
Load more

Recommended publications
  • Advances in Atomtronics
    entropy Review Advances in Atomtronics Ron A. Pepino Department of Chemistry, Biochemistry and Physics Florida Southern College, Lakeland, FL 33801, USA; rpepino@flsouthern.edu Abstract: Atomtronics is a relatively new subfield of atomic physics that aims to realize the device behavior of electronic components in ultracold atom-optical systems. The fact that these systems are coherent makes them particularly interesting since, in addition to current, one can impart quantum states onto the current carriers themselves or perhaps perform quantum computational operations on them. After reviewing the fundamental ideas of this subfield, we report on the theoretical and experimental progress made towards developing externally-driven and closed loop devices. The functionality and potential applications for these atom analogs to electronic and spintronic systems is also discussed. Keywords: atomtronics; open quantum systems; Bose–Einstein condensates; quantum simulation; quantum sensing PACS: 01.30.Rr; 03.65.Yz; 03.67.-a; 03.75.Kk; 03.75.Lm; 05.70.Ln; 06.20.-f 1. Introduction Quantum simulation has become a major research effort in atomic physics over the last three decades. Bose–Einstein condensates (BECs) have been generated, trapped, and manipulated in countless experiments, and the introduction of optical lattices has allowed Citation: Pepino, R.A. Advances in for the experimental realization of condensed matter phenomena such as the Mott insular Atomtronics. Entropy 2021, 23, 534. to superfluid phase transition and the Hofstadter butterfly [1,2]. As optical techniques https://doi.org/10.3390/e23050534 have improved, it has become possible to produce not only honeycomb [3] and Kagomé lattices [4], but custom optical lattices using holographic masks [5].
    [Show full text]
  • Atomtronics-Enabled Quantum Technologies 2
    Focus on Atomtronics-enabled Quantum Technologies Luigi Amico 1,2 Gerhard Birkl 3, Malcolm Boshier 4, and Leong-Chuan Kwek, 2,5 1 Dipartimento di Fisica e Astronomia, Universit`adi Catania & CNR-MATIS-IMM & INFN-Laboratori Nazionali del Sud, INFN, Catania 2 Centre for Quantum Technologies, National University of Singapore 3 Technische Universit¨at Darmstadt 4 Los Alamos National Laboratories 5 Institute of Advanced Studies and National Institute of Education, Nanyang Technological University, Singapore February 2014 Abstract. Atomtronics is an emerging field in quantum technology that promises to realize ’atomic circuit’ architectures exploiting ultra-cold atoms manipulated in versatile micro-optical circuits generated by laser fields of different shapes and intensities or micro-magnetic circuits known as atom chips. Although devising new applications for computation and information transfer is a defining goal of the field, Atomtronics wants to enlarge the scope of quantum simulators and to access new physical regimes with novel fundamental science. With this focus issue we want to survey the state of the art of Atomtronics-enabled Quantum Technology. We collect articles on both conceptual and applicative aspects of the field for diverse exploitations, both to extend the scope of the existing atom-based quantum devices and to devise platforms for new routes to quantum technology. arXiv:1612.07783v1 [quant-ph] 22 Dec 2016 1. Introduction The pervasive importance of electronic devices, e.g. transistors, diodes, capacitors, inductors, integrated circuits, can be observed everywhere in our daily applications and usage. The key players in electronic devices are electrons and holes. Imagine circuitry in which the carriers are atoms instead of electrons and holes.
    [Show full text]
  • Mini-Newsletter January 2012 AAAS Section on Industrial Science and Technology (Section P)
    Mini-Newsletter January 2012 AAAS Section on Industrial Science and Technology (Section P) 2012 Industrial Science and Technology Business Meeting Schedule– Please Join Us!!! Open to all meeting registrants - Come join us! Saturday, February 18, 2012: 10:00 AM-12:00 PM Oceanview Suite 3 (Pan Pacific Hotel) We hope to see you at the annual business meeting of the AAAS Section on Industrial Science and Technology that will take place Saturday morning, February 18, 2012 from 10:00 to noon in the Oceanview Suite 3 (Pan Pacific Hotel) during the AAAS Annual Meeting in Vancouver, B.C. Section Chair Carol Burns will lead the meeting. All are welcome to attend! We will provide coffee and tea service, fruit and assorted gourmet pastries at the business meeting. Minimizing our food costs allows our section to help subsidize the travel costs of speakers invited to participate in Section-P sponsored symposia. For those unable to attend the meeting, please be sure to share your ideas for next year’s technical symposia and/or topical lectures that Section P might propose/sponsor/cosponsor at the 2013 AAAS annual meeting (to be held in Boston) in advance of the February 18, 2012 business meeting. You are, of course, welcome to share your ideas and input anytime, which can be submitted to Section Secretary Anice Anderson at [email protected], or any of the other section officers listed below. We will also discuss Fellows Nominations for next year, so let us know your suggestions! Also, President of the AAAS Caribbean Division, Jorge Colón will talk to us about Haiti.
    [Show full text]
  • Universidade De São Paulo - SIICUSP: Engenharias E Exatas (15., São Carlos), 2007
    AAAppprrreeessseeennntttaaaçççãããooo PPPrrroooddduuuçççãããooo CCCiiieeennntttííífffiiicccaaa 222000000777 Sumário ARTIGO DE JORNAL-DEP/ENTR - NACIONAL.................................................................................. 13 ARTIGO DE PERIÓDICO - INTERNACIONAL..................................................................................... 13 ARTIGO DE PERIÓDICO - NACIONAL................................................................................................ 25 ARTIGO DE PERIÓDICO-DEP/ENTR - NACIONAL ............................................................................ 25 EDITOR DE PERIÓDICO - INTERNACIONAL ..................................................................................... 26 PARTE DE MONOGRAFIA/LIVRO - NACIONAL................................................................................. 26 MONOGRAFIA/LIVRO - INTERNACIONAL ......................................................................................... 26 TRABALHO DE EVENTO - INTERNACIONAL .................................................................................... 26 TRABALHO DE EVENTO - NACIONAL............................................................................................... 27 TRABALHO DE EVENTO-ANAIS PERIÓDICO - INTERNACIONAL................................................... 28 TRABALHO DE EVENTO-RESUMO – NACIONAL ............................................................................ 28 TRABALHO DE EVENTO-RESUMO - INTERNACIONAL .................................................................
    [Show full text]
  • Hypersonic Matterwaves Atomtronics
    Hypersonic Matterwaves Atomtronics Atomtronics manipulates atoms much in the way that electronics manipulates electrons. It carries the promise of highly compact quantum devices which can measure incredibly small forces or tiny rotations. [43] Now, researchers fabricated an electron's spin-filtering device that can switch the spin polarization direction by light irradiation or thermal treatment. [42] Electrospinning, a nanofiber fabrication method, can produce nanometer- to micrometer-diameter ceramic, polymer, and metallic fibers of various compositions for a wide spectrum of applications: tissue engineering, filtration, fuel cells and lithium batteries. [41] Researchers of the Nanoscience Center (NSC) at the University of Jyväskylä, Finland, and Xiamen University, China, have discovered how copper particles at the nanometer scale operate in modifying a carbon-oxygen bond when ketone molecules turn into alcohol molecules. [40] The research is carried out in the Quantum Photonics Group at the Niels Bohr Institute, which is a part of the newly established Center for Hybrid Quantum Networks (Hy-Q) [39] With international collaboration, researchers at Aalto University have now developed a nanosized amplifier to help light signals propagate through microchips. [38] Physicists at the Kastler Brossel Laboratory in Paris have reached a milestone in the combination of cold atoms and nanophotonics. [37] The universal laws governing the dynamics of interacting quantum particles are yet to be fully revealed to the scientific community. [36] Now NIST scientists have designed a vacuum gauge that is small enough to deploy in commonly used vacuum chambers. [35] A novel technique that nudges single atoms to switch places within an atomically thin material could bring scientists another step closer to realizing theoretical physicist Richard Feynman's vision of building tiny machines from the atom up.
    [Show full text]
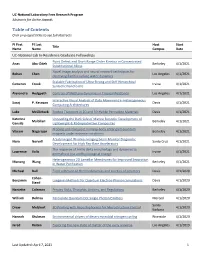
  • Table of Contents Click on Project Titles to See Full Abstracts
    UC-National Laboratory Fees Research Program Abstracts for Active Awards Table of Contents Click on project titles to see full abstracts PI First PI Last Host Start Title Name Name Campus Date UC-National Lab In-Residence Graduate Fellowships Point Defect and Short Range Order Kinetics in Concentrated Anas Abu-Odeh Berkeley 4/1/2021 Substitutional Alloys Novel image analysis and neural network techniques for Bohan Chen Los Angeles 4/1/2021 observing Earth’s surface water dynamics Scalable Fabrication of Ultra-Strong and Stiff Hierarchical Cameron Crook Irvine 4/1/2021 Syntactic Nanofoams Alexandra Hedgpeth Controls of Methane Dynamics in Tropical Peatlands Los Angeles 4/1/2021 Interactive Visual Analysis of Data Movement in Heterogeneous Suraj P. Kesavan Davis 4/1/2021 Computing Architectures Luke McClintock Exciton Transport in 2D and 3D Halide Perovskite Materials Davis 4/1/2021 Katerina Unraveling the Dark Side of Marine Biotools: Development of Malollari Berkeley 4/1/2021 Gensila Lightweight & Radioprotective Composites Probing spin transport in many-body entangled quantum Vikram Nagarajan Berkeley 4/1/2021 magnets under extreme conditions A Submerged Wireless Imaging beam Monitor Diagnostic Nora Norvell Santa Cruz 4/1/2021 Development for High Rep-Rate Accelerators The response of Arctic delta morphology and dynamics to Lawrence Vulis Irvine 4/1/2021 permafrost loss and hydrological change Heterogeneous 2D Lamellar Membranes for Improved Separation Monong Wang Berkeley 4/1/2021 in Water Purification Michael Bull From adhesion to
    [Show full text]
  • Web-Based Innovation Indicators – Which Firm Web- Site Characteristics Relate to Firm-Level Innovation Activity?
    // NO.19-063 | 12/2019 DISCUSSION PAPER // JANNA AXENBECK AND PATRICK BREITHAUPT Web-Based Innovation Indicators – Which Firm Web- site Characteristics Relate to Firm-Level Innovation Activity? Web-Based Innovation Indicators – Which Firm Website Characteristics Relate to Firm-Level Innovation Activity? Janna Axenbeck†+* & Patrick Breithaupt†* † Department of Digital Economy, ZEW – Leibniz Centre for European Economic Research, L7 1, 68161 Mannheim, Germany +Justus-Liebig-University Giessen, Faculty of Economics, Licher Straße 64, 35394 Gießen, Germany * Correspondence: [email protected]; Phone: +49 621 1235 – 188, [email protected]; Phone: +49 621 1235 – 217 December 31, 2019 Abstract Web-based innovation indicators may provide new insights into firm-level innovation activities. However, little is known yet about the accuracy and relevance of web-based information. In this study, we use 4,485 German firms from the Mannheim Innovation Panel (MIP) 2019 to analyze which website characteristics are related to innovation activities at the firm level. Website characteristics are measured by several text mining methods and are used as features in different Random Forest classification models that are compared against each other. Our results show that the most relevant website characteristics are the website’s language, the number of subpages, and the total text length. Moreover, our website characteristics show a better performance for the prediction of product innovations and innovation expenditures than for the prediction of process innovations. Keywords: Text as data, innovation indicators, machine learning JEL Classification: C53, C81, C83, O30 Acknowledgments: The authors would like to thank the German Federal Ministry of Education and Research for providing funding for the research project (TOBI - Text Data Based Output Indicators as Base of a New Innovation Metric; funding ID: 16IFI001).
    [Show full text]
  • Atomqtech Full Proposal
    ｏｰ･ｮ＠ｃ｡ｬｬ＠ｃｯｬｬ･｣ｴｩｯｮ＠ｏｃＭＲＰＱＶＭＱ ｐｲｯｰｯｳ｡ｬ＠ｒ･ｦ･ｲ･ｮ｣･＠ｏｃＭＲＰＱＶＭＱＭＲＰＵＷＴ ｔｩｴｬ･Ｚ ｑｵ｡ｮｴｵｭ＠ｔ･｣ｨｮｯｬｯｧｩ･ｳ＠ｷｩｴｨ＠ｕｬｴｲ｡Ｍｃｯｬ､＠ａｴｯｭｳ ａ｣ｲｯｮｹｭＺ ａｴｯｭｑｔ･｣ｨ ｓｵｭｭ｡ｲｹ ａｴｯｭｑｔ＠｡ｩｭｳ＠｡ｴ＠ｰｵｴｴｩｮｧ＠ｅｵｲｯｰ･＠ｩｮ＠ｴｨ･＠ｰｯｬ･＠ｰｯｳｩｴｩｯｮ＠ｩｮ＠ｴｨ･＠ｲ｡｣･＠ｴｯｷ｡ｲ､ｳ＠ｴｨ･＠ｓ･｣ｯｮ､＠ｑｵ｡ｮｴｵｭ＠ｒ･ｶｯｬｵｴｩｯｮＮ ａｴｯｭｑｔｳ＠ｭｩｳｳｩｯｮ＠ｩｳ＠ｴｨ･＠｣ｲ･｡ｴｩｯｮ＠ｯｦ＠｡＠ｬ｡ｲｧ･＠ｮ･ｴｷｯｲｫ＠ｯｦ＠･ｸｰ･ｲｴ＠ｧｲｯｵｰｳ＠ｯｮ＠｣ｯｬ､Ｍ｡ｴｯｭ＠ｱｵ｡ｮｴｵｭ＠ｰｨｹｳｩ｣ｳ＠ｴｨ｡ｴ ｷｩｬｬ＠｡｣ｴ＠｡ｳ＠｡＠｣｡ｴ｡ｬｹｳｴ＠ｩｮ＠ｴｨ･＠ｲ｡ｰｩ､＠､･ｶ･ｬｯｰｭ･ｮｴ＠｡ｮ､＠｣ｯｭｭ･ｲ｣ｩ｡ｬｩｺ｡ｴｩｯｮ＠ｯｦ＠ｱｵ｡ｮｴｵｭ＠ｴ･｣ｨｮｯｬｯｧｹ＠｢｡ｳ･､ ｯｮ＠ｵｬｴｲ｡Ｍ｣ｯｬ､＠｡ｴｯｭｳ＠｡ｮ､＠ｂｯｳ･Ｍｅｩｮｳｴ･ｩｮ＠｣ｯｮ､･ｮｳ｡ｴ･ｳＮ ｔｨ･＠ｶｩｳｩｯｮ＠ｩｳ＠ｴｯ＠･ｳｴ｡｢ｬｩｳｨ＠ｅｵｲｯｰ･＠｡ｳ＠ｴｨ･＠ｬ･｡､･ｲ＠｢ｯｴｨ＠ｩｮ＠ｦｵｮ､｡ｭ･ｮｴ｡ｬ＠ｲ･ｳ･｡ｲ｣ｨ＠｡ｳ＠ｷ･ｬｬ＠｡ｳ＠ｲ･｡ｬＭｷｯｲｬ､ ｣ｯｭｭ･ｲ｣ｩ｡ｬ＠ｰｲｯ､ｵ｣ｴｳ＠ｴｨ｡ｴ＠ｷｩｬｬ＠ｨ｡ｲｮ･ｳｳ＠ｴｨ･＠ｵｮｩｱｵ･＠ｱｵ｡ｮｴｵｭ＠ｭ･｣ｨ｡ｮｩ｣｡ｬ＠ｦ･｡ｴｵｲ･ｳ＠ｯｦ＠｣ｯｬ､＠｡ｴｯｭｩ｣ ･ｮｳ･ｭ｢ｬ･ｳＮ＠ｔｨｩｳ＠ｷｩｬｬ＠ｬ･｡､＠ｴｯ＠ｧｲｯｵｮ､｢ｲ･｡ｫｩｮｧ＠｡､ｶ｡ｮ｣･ｳ＠ｩｮ＠｡ｭｯｮｧｳｴ＠ｯｴｨ･ｲｳ＠ｭ･ｴｲｯｬｯｧｹＬ＠｣ｲｹｰｴｯｧｲ｡ｰｨｹＬ ｣ｯｭｭｵｮｩ｣｡ｴｩｯｮｳ＠｡ｮ､＠｣ｯｭｰｵｴ｡ｴｩｯｮｳＬ＠｢ｩｯｬｯｧｹＬ＠｡ｮ､＠ｧ･ｯｬｯｧｹＮ＠ａｴｯｭｑｔ＠ｷｩｬｬ＠｣ｯｮｴｲｩ｢ｵｴ･＠ｴｯ＠ｴｨｩｳ＠､･ｶ･ｬｯｰｭ･ｮｴ＠｢ｹ ｰｲｯｶｩ､ｩｮｧ＠｡＠｣ｲｵ｣ｩ｡ｬ＠ｰｬ｡ｴｦｯｲｭ＠ｦｯｲ＠ｩｮｦｯｲｭ｡ｴｩｯｮ＠･ｸ｣ｨ｡ｮｧ･＠｡ｮ､＠｣ｯｯｲ､ｩｮ｡ｴｩｯｮ＠ｯｦ＠ｲ･ｳ･｡ｲ｣ｨＮ＠ｉｴ＠ｷｩｬｬ＠｡ｬｳｯ＠｢･＠ｴｨ･ ｣｡ｴ｡ｬｹｳｴ＠ｦｯｲ＠ｴｨ･＠ｦｬ･､ｧｬｩｮｧ＠ｱｵ｡ｮｴｵｭ＠ｩｮ､ｵｳｴｲｹＮ ａ＠ｦｵｲｴｨ･ｲ＠ｰｲｩｯｲｩｴｹ＠ｯｦ＠ｴｨ･＠ａｴｯｭｑｔ＠ｮ･ｴｷｯｲｫ＠ｷｩｬｬ＠｢･＠ｯｵｴｲ･｡｣ｨＮ＠ｔｨ･＠･､ｵ｣｡ｴｩｯｮ＠ｯｦ＠ｴｨ･＠ｧ･ｮ･ｲ｡ｬ＠ｰｵ｢ｬｩ｣＠｡ｮ､＠ｴｨ･ ｩｮｦｯｲｭ｡ｴｩｯｮ＠ｰｲｯｶｩ､･､＠ｴｯ＠ｰｯｬｩ｣ｹ＠｡ｮ､＠､･｣ｩｳｩｯｮ＠ｭ｡ｫ･ｲｳ＠｡ｮ､＠Ｈｩｮｴ･ｲＩｮ｡ｴｩｯｮ｡ｬ＠ｲ･ｧｵｬ｡ｴｯｲｹ＠｢ｯ､ｩ･ｳ＠ｷｩｬｬ＠ｦ｡｣ｩｬｩｴ｡ｴ･ ｣ｯｮｳｩ､･ｲ｡｢ｬｹ＠ｴｨ･＠ｰｲｯｧｲ･ｳｳ＠ｯｦ＠ｴｨ･＠ｳ･｣ｯｮ､＠ｱｵ｡ｮｴｵｭ＠ｲ･ｶｯｬｵｴｩｯｮ＠｡ｮ､＠･ｮｳｵｲ･＠ｩｴｳ＠ｬｯｮｧ＠ｴ･ｲｭ＠ｶｩ｡｢ｩｬｩｴｹＮ ｋ･ｹ＠ｅｸｰ･ｲｴｩｳ･＠ｮ･･､･､＠ｦｯｲ＠･ｶ｡ｬｵ｡ｴｩｯｮ＠ ｐｨｹｳｩ｣｡ｬ＠ｓ｣ｩ･ｮ｣･ｳ ｕｬｴｲ｡Ｍ｣ｯｬ､＠｡ｴｯｭｳ＠｡ｮ､＠ｭｯｬ･｣ｵｬ･ｳ ｋ･ｹｷｯｲ､ｳ ｑｵ｡ｮｴｵｭ＠ｔ･｣ｨｮｯｬｯｧｩ･ｳ ｕｬｴｲ｡Ｍｃｯｬ､＠ａｴｯｭｳ ｑｵ｡ｮｴｵｭ＠ｓ･ｮｳｯｲｳ＠｡ｮ､＠ａｰｰｬｩ｣｡ｴｩｯｮｳ Powered by TCPDF (www.tcpdf.org) TECHNICAL ANNEX 1.
    [Show full text]
  • Basic Research
    Report of the Defense Science Board Task Force on Basic Research January 2012 Office of the Under Secretary of Defense for Acquisition, Technology and Logistics Washington, D.C. 20301-3140 This report is a product of the Defense Science Board (DSB). The DSB is a Federal Advisory Committee established to provide independent advice to the Secretary of Defense. Statements, opinions, conclusions, and recommendations in this report do not necessarily represent the official position of the Department of Defense (DOD). The DSB Task Force on Basic Research completed its information gathering in April 2011. The report was cleared for open publication by the DOD Office of Security Review on December 7, 2011. This report is unclassified and cleared for public release. OFFICE OF THE SECRETARY OF DEFENSE 3140 DEFENSE PENTAGON WASHINGTON, DC 20301 - 3140 DEFENSE SCIENCE BOARD MEMORANDUM FOR UNDER SECRETARY OF DEFENSE FOR ACQUISITION, TECHNOLOGY, AND LOGISTICS SUBJECT: Report of the Defense Science Board Task Force on Basic Research I am pleased to forward the final report of the Defense Science Board Task Force on Basic Research. The report offers important considerations for the Department of Defense to maintain a world-dominating lead in basic research. Beginning with efTorts supporting World War II, the United States built a commanding scientific infrastructure second to none, and reaped considerable military and economic benefits as a result. The task force took on the task to both validate the quality of the existing DoD basic research program and to provide advice on long-term basic research planning and strategies. Overall, the task force found the current DoD basic research program to be a very good one, comparable to other basic research programs in the government and well-suited to DoD needs.
    [Show full text]
  • Holey Fibers & Photonic Crystals
    SUMMER TOPICALS MEETING SERIES 2017 PROGRAM – AT – A – GLANCE OPTICAL SWITCHING INTEGRATED PHOTONICS INTEGRATED LOW ENERGY TECHNOLOGIES FOR FOR THE ULTRAVIOLET PHOTONICS RESEARCH FOR QUANTUM NETWORKS PHOTONICS FOR THE INTEGRATED DATACOM AND AND VISIBLE SPECTRAL 5G AND BEYOND (PR5G) (QNW) MID-INFRARED (IPUV) NANOPHOTONICS (LEIN) COMPUTERCOM RANGE (IPMI) APPLICATIONS (OSDC) Room: MIRAMAR ATLANTIC I ATLANTIC II BALLROOM I BALLROOM II BALLROOM III BALLROOM IV Tuesday, 11 July 8:00 – 8:30 CONTINENTAL BREAKFAST – Grand Ballroom Foyer TuA1: GeSn Materials TuB1: III-Nitride TuC1: Attojoule TuE1: 5G Standards and TuF1: Quantum 8:30 – 10:00 and Devices IV Photonics Photonics LEIN/OSDC Field Trials Channels and joint session Decoherence 10:00 – 10:30 COFFEE BREAK – Grand Ballroom Foyer TuA2: Novel Integration TuB2: Photonic TuC2: Integrated TuD2: Optically TuE2: 5G Perspectives from TuF2: Sources of Technology Circuits and Sources for Nanophotonics Switched Data Center Industry and Academia Entangled Photon Pairs 10:30 – 12:00 Quantum Information Network Architectures and Optical Switching Systems I 12:00 – 1:30 LUNCH ON OWN TuA3: Si Based Mid-IR TuB3: TuC3: Nanophotonics TuD3: Optically TuE3: High Data Rate TuF3: Long Distance Nanobiophotonics and for High-Speed Switched Data Center Wireless Quantum Communication 1:30 – 3:00 Spectroscopy Network Architectures and Optical Switching Systems II 3:00 – 3:30 COFFEE BREAK – Grand Ballroom Foyer TuA4: Novel Si Based TuC4: Nanophotonic TuD4: Optically TuE4: Beyond 5G TuF4: Structure of Integrated Photonics
    [Show full text]
  • Session at AAAS Annual Meeting
    SESSION on DESIGN THINKING TO MOBILIZE SCIENCE, TECHNOLOGY AND INNOVATION FOR SOCIAL CHALLENGES The aim of this symposium is to highlight the innova- tive approaches towards address social challenges. There has been growing interest in promoting “social innovation” to imbed innovation in the wider economy by fostering opportunities for new actors, such as non-profit foundations, to steer research and collaborate with firms and entrepreneurs and to tackle social challenges. User and consumers are also relevant as they play an important role in demanding innovation for social goals but also as actors and suppliers of solutions. Although the innovation process is now much more open and receptive to social influences, progress on social innovation will call for the greater involvement of stakeholders who can mobilize science, technol- ogy and innovation to address social challenges. Thus, the session requires to be approached from holistic and multidisciplinary mind and needs to cover the issue from different aspects by seven inter- national speakers. Contents Overview ■1 Program ■4 Session Description ■6 Outline of Presentation ■7 Lecture material ■33 Appendix ■55 Program Welcome and Opening 8:30-8:35 • Dr. Yuko Harayama, Deputy Director of the OECD’s Directorate for Science, Technology and Industry (DSTI) ● (moderator) (5min) Session 1: Putting ‘design thinking’ into practice 8:35-9:20 • Dr. Karabi Acharya, Change Leader, Ashoka, USA(15min) ● Systemic Change to Achieve Environmental Impact and Sustainability • Mr. Tateo Arimoto, Director-General, Research Institute of Science and Technology for Society, Japan Science and Technology Agency (JST / RISTEX) (Co-organiser and Host), Japan (15min) Design Thinking to Induce new paradigm for issue-driven approach −Discussant (5min) • Dr.
    [Show full text]
  • Science Without Borders 17–21 February, Washington, D.C
    Preliminary Press Program Join Us in Washington, D.C. for Science and Fun Cover symposia on the implications of finding other worlds, the next steps in brain-computer interfaces, frontiers in chemistry, the next big solar storm, and more. Talk to leaders in science, technology, engineering, education, and policy-making. Gather story ideas for the year ahead. Mingle with colleagues at receptions and social events. It’s all available at the world’s largest interdisciplinary science forum. 2011 AAAS Annual Meeting Science Without Borders 17–21 February, Washington, D.C. CURRENT AS OF 1 NOVEMBER 2010 1 2011 AAAS Annual Meeting Science Without Borders Dear Colleagues, On behalf of the AAAS Board of Directors, it is my distinct honor to invite you to the 177th Meeting of the American Association for the Advancement of Science (AAAS). The Annual Meeting is one of the most widely recognized pan-science events, with hundreds of networking oppor- tunities and broad global media coverage. An exceptional array of speakers and attendees will gather at the Walter E. Washington Convention Center in Washington, D.C. You will have the opportunity to interact with scientists, engineers, educators, and policy-makers who will present the latest thinking and developments in their areas of expertise. The meeting’s theme — Science Without Borders — integrates interdisciplinary science, across both research and teaching, that utilizes diverse approaches as well as the diversity of its practitioners. The program will highlight science and teaching that cross conventional borders or break out from silos, especially in ground-breaking areas of research that highlight new and exciting developments in support of science, technology, and education.
    [Show full text]