DOCSLIB.ORG

Unit 11(Exponents & Powers)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Unit 11(Exponents & Powers) • Exponents are used to express large numbers in shorter form to make them easy to read, understand, compare and operate upon. • a × a × a × a = a4 (read as ‘a’ raised to the exponent 4 or the fourth power of a), where ‘a’ is the base and 4 is the exponent and a4 is called the exponential form. a × a × a × a is called the expanded form. • For any non-zero integers ‘a’ and ‘b’ and whole numbers m and n, (i) am × an = am+n (ii) am ÷ an = am–n , m>n (iii) (am)n = amn (iv) am × bm = ( ab)m m a (v) am ÷ bm = b (vi) a0 = 1 (vii) (–1)even number = 1 (viii) (–1)odd number = –1 • Any number can be expressed as a decimal number between 1.0 and 10.0 (including 1.0) multiplied by a power of 10. Such form of a number is called its standard form or scientific notation. 15-04-2018 In Examples 1 to 3, there are four options, out of which one is correct. Write the correct one. – 8 Example 1: Out of the following, the number which is not equal to is 27 3 3 2 −2 (a) – (b) 3 3 3 −2 −−−222 (c) – (d) ×× 3 333 Solution: Correct answer is (c). Example 2: ()()−775 ×− 3 is equal to (a) ()−7 8 (b) – ()7 8 (c) ()−7 15 (d) ()−7 2 Solution: Correct answer is (a). Example 3: For any two non-zero integers x any y, x3 ÷ y3 is equal to 0 3 æöx x (a) ç÷ (b) èøy y 6 9 æöx æöx (c) èøç÷y (d) èøç÷y Solution: Correct answer is (b). Words Numbers Algebra To multiply powers m n m+n with the same base, 35 × 38 = 3 5 + 8 = 3 13 b × b = b keep the base and add the exponents. In Examples 4 and 5, fill in the blanks to make the statements true. 2 Example 4: (5576÷ ) = ________ Solution: 52 15-04-2018 ab73 Example 5: = __________ ab5 Solution: (ab)2 In Examples 6 to 8, state whether the statements are True or False: Example 6: In the number 75, 5 is the base and 7 is the exponent. Solution: False A power is written in base and exponent form as follows: The base is the number that Þ The exponent tells you is being repeated as a factor Þ 52 how many times the base in the multiplication. is repeated as a factor in the multiplication For example 7.7 = 72, 3•3•3•3•3 = 35. a4 aaaa+++ Example 7: = b3 bbb++ Solution: False Example 8: ab > b a is true, if a = 3 and b = 4; but false, if a = 2 and b = 3. Solution: True Example 9: By what number should we multiply 3 3 so that the product may be equal to 37? Solution: Let 33 be multiplied by x so that the product may be equal to 37. According to question, 3 3 × x = 37 or x = 37 ÷ 33 = (3)7–3 (Using am ÷ an = (a)m–n ) = 34 = 81 Therefore, 33 should be multiplied by 81 so that the product is equal to 37. 15-04-2018 5 11 8x 55 5 Example 10: Find x so that ×= 33 3 5 11 8x 55 5 Solution: Given ×= 33 3 m 555 11 58 x aam ×= Using = So, 5 11 m 33 3 b b 555× 11 58 x = or 5 11 33× 3 8 x (5)16 5 m n m+n or 16 = {Using a × a = (a) } (3)3 16 8 x 55 or = 33 or 16 = 8x Thus, 8x = 16 Therefore, x = 2 Example 11: Express 648 in exponential notation. 2 648 Solution: 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 2 324 = 23 × 34 2 162 Express 2,36,00,000 in standard Example 12: 3 81 form. Solution: 236,00,000 3 27 236,00,000 39 = ×100,00,000 100,00,000 33 = 2.36 × 107 1 Example 13: Which of the two is larger : 312 or 66 ? Solution: 312 = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 531441 66 = 6 × 6 × 6 × 6 × 6 × 6 = 46656 So, 312 is greater. 15-04-2018 Example 14 1 5 1 19 1 8x Find x such that × = 5 5 5 Solution: Understand and Explore the Problem • What are you trying to find? The value of x for the given equation. Plan a Strategy • You know the laws of exponents. Apply those laws in the given equation to find the value of x. Solve 1 5 1 19 1 8x • Given, × = 5 5 5 Using the law of exponents, am × an = am+n, we get + 1 5 19 1 8x = 5 5 1 24 1 8x = 5 5 On both the sides, powers have the same base. So, their exponents must be equal Therefore, 24 = 8x 24 or x==3 8 Hence, the value of x is 3. 15-04-2018 Revise • Substitute the value of x in the equation and check if it satisfies the equation. + 1 5 1 19 1 5 19 1 24 LHS = × = = 5 5 5 5 × 1 8x 1 83 1 24 RHS = = = 5 5 5 LHS = RHS Hence, the equation is satisfied with x = 3. So, our answer is correct. 1 3 1. Try to find the value of x given in the question by changing to . 5 2 What difference do you find in the value of x ? What do you infer from your answer? 2. Can you find the value of x if the equation is changed to (5)x ÷ (5)2 = (5)3 ? In questions 1 to 22, there are four options, out of which one is correct. Write the correct one. 1. [(–3)2]3 is equal to (a) (–3)8 (b) (–3)6 (c) (–3)5 (d) (–3)23 2. For a non-zero rational number x, xx82÷ is equal to (a) x4 (b) x6 (c) x10 (d) x16 3. x is a non-zero rational number. Product of the square of x with the cube of x is equal to the (a) second power of x (b) third power of x (c) fifth power of x (d) sixth power of x 15-04-2018 4. For any two non-zero rational numbers x and y, xy55÷ is equal to (a) (x÷y)1 (b) (x÷y)0 (c) (x÷y)5 (d) (x÷y)10 5. am × an is equal to (a) (a2)mn (b) am–n (c) am+n (d) amn 6. (10 + 20 + 30) is equal to (a) 0 (b) 1 (c) 3 (d) 6 1022+ 10 20 7. Value of is 1020 (a) 10 (b) 1042 (c) 101 (d) 1022 8. The standard form of the number 12345 is (a) 1234.5 × 101 (b) 123.45 × 102 (c) 12.345 × 103 (d) 1.2345 × 104 9. If 21998 – 21997 – 21996 + 21995 = K.21995, then the value of K is (a) 1 (b) 2 (c) 3 (d) 4 10. Which of the follwing is equal to 1? (a) 20 + 30 + 40 (b) 20 × 30 × 40 (c) (30 – 2 0) × 40 (d) (30 – 2 0) × (30 +20) 11. In standard form, the number 72105.4 is written as 7.21054 × 10n where n is equal to (a) 2 (b) 3 (c) 4 (d) 5 −2 12. Square of is 3 −2 2 −4 4 (a) (b) (c) (d) 3 3 9 9 Words Numbers Algebra To divide powers with the same base, keep m 9 b mn– 6 9–4 5 =b the base and subtract ==66 n 4 b the exponents. 6 15-04-2018 Product of Powers Property Words To multiply powers with the same base, add their exponents. Algebra am . an = am + n Numbers 56 . 53 = 56 + 3 = 59 −1 13. Cube of is 4 –1 1 −1 1 (a) (b) (c) (d) 12 16 64 64 4 – 5 14. Which of the following is not equal to ? 4 4 (– 5)4 5 (a) (b) 4 44 ( – 4 ) 4 5 55 5 5 (c) – (d) − ×− × − ×− 44 4 4 4 4 15. Which of the following is not equal to 1 ? 32 23× 7 −34 ×− ÷−()2 (a) 4× 18 (b) ()()22 303 ×5 24 (c) (d) 0 03 5×25 (7 +3 ) 33 25 16. × is equal to 37 9 6 3 0 25 25 25 25 (a) × (b) × (c) × (d) × 37 37 37 37 17. In standard form, the number 829030000 is written as K × 108 where K is equal to (a) 82903 (b) 829.03 (c) 82.903 (d) 8.2903 15-04-2018 18. Which of the following has the largest value? 1 1 1 (a) 0.0001 (b) (c) (d) ÷ 0.1 10000 106 106 19. In standard form 72 crore is written as (a) 72 × 107 (b) 72 × 108 (c) 7.2 × 108 (d) 7.2 × 107 mn aa 20. For non-zero numbers a and b, ÷ , where m > n, is equal to bb mn m + n m – n m n a a a a (a) (b) (c) (d) b b b b 21. Which of the following is not true? (a) 32 > 23 (b) 43 = 26 (c) 33 = 9 (d) 25 > 52 22. Which power of 8 is equal to 26? (a) 3 (b) 2 (c) 1 (d) 4 In questions 23 to 39, fill in the blanks to make the statements true. 23. (–2)31 × (–2)13 = (–2) 24. (–3)8 ÷ (–3)5 = (–3) 4 9 3 _____ 11 11 5 11 –1 –1 –1 25.
Load more

Recommended publications
  • Large but Finite
    Department of Mathematics MathClub@WMU Michigan Epsilon Chapter of Pi Mu Epsilon Large but Finite Drake Olejniczak Department of Mathematics, WMU What is the biggest number you can imagine? Did you think of a million? a billion? a septillion? Perhaps you remembered back to the time you heard the term googol or its show-off of an older brother googolplex. Or maybe you thought of infinity. No. Surely, `infinity' is cheating. Large, finite numbers, truly monstrous numbers, arise in several areas of mathematics as well as in astronomy and computer science. For instance, Euclid defined perfect numbers as positive integers that are equal to the sum of their proper divisors. He is also credited with the discovery of the first four perfect numbers: 6, 28, 496, 8128. It may be surprising to hear that the ninth perfect number already has 37 digits, or that the thirteenth perfect number vastly exceeds the number of particles in the observable universe. However, the sequence of perfect numbers pales in comparison to some other sequences in terms of growth rate. In this talk, we will explore examples of large numbers such as Graham's number, Rayo's number, and the limits of the universe. As well, we will encounter some fast-growing sequences and functions such as the TREE sequence, the busy beaver function, and the Ackermann function. Through this, we will uncover a structure on which to compare these concepts and, hopefully, gain a sense of what it means for a number to be truly large. 4 p.m. Friday October 12 6625 Everett Tower, WMU Main Campus All are welcome! http://www.wmich.edu/mathclub/ Questions? Contact Patrick Bennett ([email protected]) .
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • A Child Thinking About Infinity
    A Child Thinking About Infinity David Tall Mathematics Education Research Centre University of Warwick COVENTRY CV4 7AL Young children’s thinking about infinity can be fascinating stories of extrapolation and imagination. To capture the development of an individual’s thinking requires being in the right place at the right time. When my youngest son Nic (then aged seven) spoke to me for the first time about infinity, I was fortunate to be able to tape-record the conversation for later reflection on what was happening. It proved to be a fascinating document in which he first treated infinity as a very large number and used his intuitions to think about various arithmetic operations on infinity. He also happened to know about “minus numbers” from earlier experiences with temperatures in centigrade. It was thus possible to ask him not only about arithmetic with infinity, but also about “minus infinity”. The responses were thought-provoking and amazing in their coherent relationships to his other knowledge. My research in studying infinite concepts in older students showed me that their ideas were influenced by their prior experiences. Almost always the notion of “limit” in some dynamic sense was met before the notion of one to one correspondences between infinite sets. Thus notions of “variable size” had become part of their intuition that clashed with the notion of infinite cardinals. For instance, Tall (1980) reported a student who considered that the limit of n2/n! was zero because the top is a “smaller infinity” than the bottom. It suddenly occurred to me that perhaps I could introduce Nic to the concept of cardinal infinity to see what this did to his intuitions.
    [Show full text]
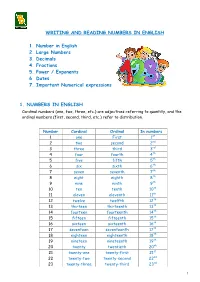
  • WRITING and READING NUMBERS in ENGLISH 1. Number in English 2
    WRITING AND READING NUMBERS IN ENGLISH 1. Number in English 2. Large Numbers 3. Decimals 4. Fractions 5. Power / Exponents 6. Dates 7. Important Numerical expressions 1. NUMBERS IN ENGLISH Cardinal numbers (one, two, three, etc.) are adjectives referring to quantity, and the ordinal numbers (first, second, third, etc.) refer to distribution. Number Cardinal Ordinal In numbers 1 one First 1st 2 two second 2nd 3 three third 3rd 4 four fourth 4th 5 five fifth 5th 6 six sixth 6th 7 seven seventh 7th 8 eight eighth 8th 9 nine ninth 9th 10 ten tenth 10th 11 eleven eleventh 11th 12 twelve twelfth 12th 13 thirteen thirteenth 13th 14 fourteen fourteenth 14th 15 fifteen fifteenth 15th 16 sixteen sixteenth 16th 17 seventeen seventeenth 17th 18 eighteen eighteenth 18th 19 nineteen nineteenth 19th 20 twenty twentieth 20th 21 twenty-one twenty-first 21st 22 twenty-two twenty-second 22nd 23 twenty-three twenty-third 23rd 1 24 twenty-four twenty-fourth 24th 25 twenty-five twenty-fifth 25th 26 twenty-six twenty-sixth 26th 27 twenty-seven twenty-seventh 27th 28 twenty-eight twenty-eighth 28th 29 twenty-nine twenty-ninth 29th 30 thirty thirtieth 30th st 31 thirty-one thirty-first 31 40 forty fortieth 40th 50 fifty fiftieth 50th 60 sixty sixtieth 60th th 70 seventy seventieth 70 th 80 eighty eightieth 80 90 ninety ninetieth 90th 100 one hundred hundredth 100th 500 five hundred five hundredth 500th 1,000 One/ a thousandth 1000th thousand one thousand one thousand five 1500th 1,500 five hundred, hundredth or fifteen hundred 100,000 one hundred hundred thousandth 100,000th thousand 1,000,000 one million millionth 1,000,000 ◊◊ Click on the links below to practice your numbers: http://www.manythings.org/wbg/numbers-jw.html https://www.englisch-hilfen.de/en/exercises/numbers/index.php 2 We don't normally write numbers with words, but it's possible to do this.
    [Show full text]
  • The Observability of the Fibonacci and the Lucas Cubes
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Mathematics 255 (2002) 55–63 www.elsevier.com/locate/disc The observability of the Fibonacci and the Lucas cubes Ernesto DedÃo∗;1, Damiano Torri1, Norma Zagaglia Salvi1 Dipartimento di Matematica, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133 Milano, Italy Received 5 April 1999; received inrevised form 31 July 2000; accepted 8 January2001 Abstract The Fibonacci cube n is the graph whose vertices are binary strings of length n without two consecutive 1’s and two vertices are adjacent when their Hamming distance is exactly 1. If the binary strings do not contain two consecutive 1’s nora1intheÿrst and in the last position, we obtainthe Lucas cube Ln. We prove that the observability of n and Ln is n, where the observability of a graph G is the minimum number of colors to be assigned to the edges of G so that the coloring is proper and the vertices are distinguished by their color sets. c 2002 Elsevier Science B.V. All rights reserved. MSC: 05C15; 05A15 Keywords: Fibonacci cube; Fibonacci number; Lucas number; Observability 1. Introduction A Fibonacci string of order n is a binary string of length n without two con- secutive ones. Let and ÿ be binary strings; then ÿ denotes the string obtained by concatenating and ÿ. More generally, if S is a set of strings, then Sÿ = {ÿ: ∈ S}. If Cn denotes the set of the Fibonacci strings of order n, then Cn+2 =0Cn+1 +10Cn and |Cn| = Fn, where Fn is the nth Fibonacci number.
    [Show full text]
  • Simple Statements, Large Numbers
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Simple Statements, Large Numbers Shana Streeks University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Streeks, Shana, "Simple Statements, Large Numbers" (2007). MAT Exam Expository Papers. 41. https://digitalcommons.unl.edu/mathmidexppap/41 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Master of Arts in Teaching (MAT) Masters Exam Shana Streeks In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Gordon Woodward, Advisor July 2007 Simple Statements, Large Numbers Shana Streeks July 2007 Page 1 Streeks Simple Statements, Large Numbers Large numbers are numbers that are significantly larger than those ordinarily used in everyday life, as defined by Wikipedia (2007). Large numbers typically refer to large positive integers, or more generally, large positive real numbers, but may also be used in other contexts. Very large numbers often occur in fields such as mathematics, cosmology, and cryptography. Sometimes people refer to numbers as being “astronomically large”. However, it is easy to mathematically define numbers that are much larger than those even in astronomy. We are familiar with the large magnitudes, such as million or billion.
    [Show full text]
  • 1 Powers of Two
    A. V. GERBESSIOTIS CS332-102 Spring 2020 Jan 24, 2020 Computer Science: Fundamentals Page 1 Handout 3 1 Powers of two Definition 1.1 (Powers of 2). The expression 2n means the multiplication of n twos. Therefore, 22 = 2 · 2 is a 4, 28 = 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 is 256, and 210 = 1024. Moreover, 21 = 2 and 20 = 1. Several times one might write 2 ∗ ∗n or 2ˆn for 2n (ˆ is the hat/caret symbol usually co-located with the numeric-6 keyboard key). Prefix Name Multiplier d deca 101 = 10 h hecto 102 = 100 3 Power Value k kilo 10 = 1000 6 0 M mega 10 2 1 9 1 G giga 10 2 2 12 4 T tera 10 2 16 P peta 1015 8 2 256 E exa 1018 210 1024 d deci 10−1 216 65536 c centi 10−2 Prefix Name Multiplier 220 1048576 m milli 10−3 Ki kibi or kilobinary 210 − 230 1073741824 m micro 10 6 Mi mebi or megabinary 220 40 n nano 10−9 Gi gibi or gigabinary 230 2 1099511627776 −12 40 250 1125899906842624 p pico 10 Ti tebi or terabinary 2 f femto 10−15 Pi pebi or petabinary 250 Figure 1: Powers of two Figure 2: SI system prefixes Figure 3: SI binary prefixes Definition 1.2 (Properties of powers). • (Multiplication.) 2m · 2n = 2m 2n = 2m+n. (Dot · optional.) • (Division.) 2m=2n = 2m−n. (The symbol = is the slash symbol) • (Exponentiation.) (2m)n = 2m·n. Example 1.1 (Approximations for 210 and 220 and 230).
    [Show full text]
  • On Hardy's Apology Numbers
    ON HARDY’S APOLOGY NUMBERS HENK KOPPELAAR AND PEYMAN NASEHPOUR Abstract. Twelve well known ‘Recreational’ numbers are generalized and classified in three generalized types Hardy, Dudeney, and Wells. A novel proof method to limit the search for the numbers is exemplified for each of the types. Combinatorial operators are defined to ease programming the search. 0. Introduction “Recreational Mathematics” is a broad term that covers many different areas including games, puzzles, magic, art, and more [31]. Some may have the impres- sion that topics discussed in recreational mathematics in general and recreational number theory, in particular, are only for entertainment and may not have an ap- plication in mathematics, engineering, or science. As for the mathematics, even the simplest operation in this paper, i.e. the sum of digits function, has application outside number theory in the domain of combinatorics [13, 26, 27, 28, 34] and in a seemingly unrelated mathematical knowledge domain: topology [21, 23, 15]. Pa- pers about generalizations of the sum of digits function are discussed by Stolarsky [38]. It also is a surprise to see that another topic of this paper, i.e. Armstrong numbers, has applications in “data security” [16]. In number theory, functions are usually non-continuous. This inhibits solving equations, for instance, by application of the contraction mapping principle because the latter is normally for continuous functions. Based on this argument, questions about solving number-theoretic equations ramify to the following: (1) Are there any solutions to an equation? (2) If there are any solutions to an equation, then are finitely many solutions? (3) Can all solutions be found in theory? (4) Can one in practice compute a full list of solutions? arXiv:2008.08187v1 [math.NT] 18 Aug 2020 The main purpose of this paper is to investigate these constructive (or algorith- mic) problems by the fixed points of some special functions of the form f : N N.
    [Show full text]
  • Figurate Numbers
    Figurate Numbers by George Jelliss June 2008 with additions November 2008 Visualisation of Numbers The visual representation of the number of elements in a set by an array of small counters or other standard tally marks is still seen in the symbols on dominoes or playing cards, and in Roman numerals. The word "calculus" originally meant a small pebble used to calculate. Bear with me while we begin with a few elementary observations. Any number, n greater than 1, can be represented by a linear arrangement of n counters. The cases of 1 or 0 counters can be regarded as trivial or degenerate linear arrangements. The counters that make up a number m can alternatively be grouped in pairs instead of ones, and we find there are two cases, m = 2.n or 2.n + 1 (where the dot denotes multiplication). Numbers of these two forms are of course known as even and odd respectively. An even number is the sum of two equal numbers, n+n = 2.n. An odd number is the sum of two successive numbers 2.n + 1 = n + (n+1). The even and odd numbers alternate. Figure 1. Representation of numbers by rows of counters, and of even and odd numbers by various, mainly symmetric, formations. The right-angled (L-shaped) formation of the odd numbers is known as a gnomon. These do not of course exhaust the possibilities. 1 2 3 4 5 6 7 8 9 n 2 4 6 8 10 12 14 2.n 1 3 5 7 9 11 13 15 2.n + 1 Triples, Quadruples and Other Forms Generalising the divison into even and odd numbers, the counters making up a number can of course also be grouped in threes or fours or indeed any nonzero number k.
    [Show full text]
  • Grade 7 Mathematics Strand 6 Pattern and Algebra
    GR 7 MATHEMATICS S6 1 TITLE PAGE GRADE 7 MATHEMATICS STRAND 6 PATTERN AND ALGEBRA SUB-STRAND 1: NUMBER PATTERNS SUB-STRAND 2: DIRECTED NUMBERS SUB-STRAND 3: INDICES SUB-STARND 4: ALGEBRA GR 7 MATHEMATICS S6 2 ACKNOWLEDGEMENT Acknowledgements We acknowledge the contributions of all Secondary and Upper Primary Teachers who in one way or another helped to develop this Course. Special thanks to the Staff of the mathematics Department of FODE who played active role in coordinating writing workshops, outsourcing lesson writing and editing processes, involving selected teachers of Madang, Central Province and NCD. We also acknowledge the professional guidance provided by the Curriculum Development and Assessment Division throughout the processes of writing and, the services given by the members of the Mathematics Review and Academic Committees. The development of this book was co-funded by GoPNG and World Bank. MR. DEMAS TONGOGO Principal- FODE . Written by: Luzviminda B. Fernandez SCO-Mathematics Department Flexible Open and Distance Education Papua New Guinea Published in 2016 @ Copyright 2016, Department of Education Papua New Guinea All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means electronic, mechanical, photocopying, recording or any other form of reproduction by any process is allowed without the prior permission of the publisher. ISBN: 978 - 9980 - 87 - 250 - 0 National Library Services of Papua New Guinea Printed by the Flexible, Open and Distance Education GR 7 MATHEMATICS S6 3 CONTENTS CONTENTS Page Secretary‟s Message…………………………………….…………………………………......... 4 Strand Introduction…………………………………….…………………………………………. 5 Study Guide………………………………………………….……………………………………. 6 SUB-STRAND 1: NUMBER PATTERNS ……………...….……….……………..………..
    [Show full text]
  • A Quantum Primality Test with Order Finding
    A quantum primality test with order finding Alvaro Donis-Vela1 and Juan Carlos Garcia-Escartin1,2, ∗ 1Universidad de Valladolid, G-FOR: Research Group on Photonics, Quantum Information and Radiation and Scattering of Electromagnetic Waves. o 2Universidad de Valladolid, Dpto. Teor´ıa de la Se˜nal e Ing. Telem´atica, Paseo Bel´en n 15, 47011 Valladolid, Spain (Dated: November 8, 2017) Determining whether a given integer is prime or composite is a basic task in number theory. We present a primality test based on quantum order finding and the converse of Fermat’s theorem. For an integer N, the test tries to find an element of the multiplicative group of integers modulo N with order N − 1. If one is found, the number is known to be prime. During the test, we can also show most of the times N is composite with certainty (and a witness) or, after log log N unsuccessful attempts to find an element of order N − 1, declare it composite with high probability. The algorithm requires O((log n)2n3) operations for a number N with n bits, which can be reduced to O(log log n(log n)3n2) operations in the asymptotic limit if we use fast multiplication. Prime numbers are the fundamental entity in number For a prime N, ϕ(N) = N 1 and we recover Fermat’s theory and play a key role in many of its applications theorem. − such as cryptography. Primality tests are algorithms that If we can find an integer a for which aN−1 1 mod N, determine whether a given integer N is prime or not.
    [Show full text]
  • Tutor Talk Binary Numbers
    What are binary numbers and why do we use them? BINARY NUMBERS Converting decimal numbers to binary numbers The number system we commonly use is decimal numbers, also known as Base 10. Ones, tens, hundreds, and thousands. For example, 4351 represents 4 thousands, 3 hundreds, 5 tens, and 1 ones. Thousands Hundreds Tens ones 4 3 5 1 Thousands Hundreds Tens ones 4 3 5 1 However, a computer does not understand decimal numbers. It only understands “on and off,” “yes and no.” Thousands Hundreds Tens ones 4 3 5 1 In order to convey “yes and no” to a computer, we use the numbers one (“yes” or “on”) and zero (“no” or “off”). To break it down further, the number 4351 represents 1 times 1, 5 times 10, DECIMAL NUMBERS (BASE 10) 3 times 100, and 4 times 1000. Each step to the left is another multiplication of 10. This is why it is called Base 10, or decimal numbers. The prefix dec- 4351 means ten. 4x1000 3x100 5x10 1x1 One is 10 to the zero power. Anything raised to the zero power is one. DECIMAL NUMBERS (BASE 10) Ten is 10 to the first power (or 10). One hundred is 10 to the second power (or 10 times 10). One thousand is 10 to the third 4351 power (or 10 times 10 times 10). 4x1000 3x100 5x10 1x1 103=1000 102=100 101=10 100=1 Binary numbers, or Base 2, use the number 2 instead of the number 10. 103 102 101 100 The prefix bi- means two.
    [Show full text]