DOCSLIB.ORG

Lawrence Berkeley National Laboratory Recent Work

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lawrence Berkeley National Laboratory Recent Work Lawrence Berkeley National Laboratory Recent Work Title E.E. REVIEW COURSE - LECTURE VIII. Permalink https://escholarship.org/uc/item/733807j5 Authors Martinelli, E. Leppard, J. Perl, H. Publication Date 1952-04-21 eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA UCRT. 1888 Radiation Laboratory Berkeley, California ELECTRICAL ENGINEERING REVIEW COURSE LECTURE VIII April 21, 1952 E. Martinelli (Notes by: J. Leppard, H. -Perl) I. MAG1TETIC FIELDS A. Electrostatic Case Coulomb's Law which is given for th~ electrostatic case can be stated thus~ 2 ~ F = f e1 e2 / r in which F is in dynes, r in centimeters, f = 1 (dimensionless}j'l-gives the value of the charge e, in electro­ static units (ESU). B. Magnetic Case The magnetic case has an equivalent which was first determined "experi­ mentally by Ampere. Given two closed loops of wire of length~. Using electromagnetic units (EMU) i is measured in ab amperes = 10 amperes. r is measured in centimeters.· C = 1 (dimensionless). DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California. UCRL 1888 dl is in dynes Using !\IlKS units Yis measured in Newtons i is measured in amperes 1. is measured in meters C = -'-'-' ~= permeability of free space) 4'11' = 41f x 10-7 Henries/meter = volt sec/amp. The relationship of these two systems of units is: 1 EMU of current = 3 x 1010 ESU charge/seco An expression for the magnetic field due to an infinitesimal current is: 2 dl = 12 dJ..2 x r/~ then dy =-il di.~ x-~ / Inte'grating yields an integral formula for calculating Jt. -t =fi d·-f.x ~·- r2 As shown, this formula gives an answer in EMU units. For MKS units in­ sert the constant The units of magnetic field are: MKS = Webers/meter2 ErVIU = Gauss and 1 Weber = volt second 1 Gauss = lo-4 Webers/m2 II. MAGNET DESIGN In the design of a small magnet with a small gap, analogous cases can be formulated using a more familiar group of functions. Consider a loop of copper wire about a dielectric (Fig. 1) with an impres­ sed voltage potential v1 and v2 as compared with a small electro-magnet (Fig. 2). - 3 - UCRL 1888 MAGNETIC I~~UCTION (assuming the divergence of the current in the conductor = 0) Expressed thus: \J•i=O ~ .-r= 0 then· t · J, = 4'11I (total J ~. · current) (differential form of Ohm's Law) assuming ..)J-7= P! 4'11" I = MMF (..u..is equivalent to conductivity) fAA I =..J i n ds (total current through N :fi· ~ds conductor) R = E/I R' =...11.. (R 1. = reluctance) N R1 = L ~A - 4- --.... ·. Having "defined the term reluctance (R'), consider an elecfro-magnet and its air gap of length L with cross sectional area A (Fig. 3} L. R1 Gap = L Gap (Neglect Fringe vo--.-:___r­ A Gap Effects) ,, R' Iron = L Iron '-A A IronJJ- ~/(3.,9 therefore, for an efficient magnet design: R' gap considering the flux (N) or· the gap: Ngap = Bgap Agap (in Gauss). = Jl.. R' = 4 '11'" n I Agap, when n I is ab ampere turns Lgap ~ Z Bgap Lgap (Lin inches) 1 B in Gauss ...... · These formulae assume no field outside the magnet and that ~ does not saturate the iron. - 5 ~. UCRL 1888 III. MAGNETIC SHIELDING The problem of m~gnetic shielding can be considered as follciws: Assume a uniform magnetic field (Figo 5) I I I CASE lo (P! l to the iron. Jt is continous) o Biron = Bair Hiron = Biron . '. -~ CASE 2o .(P! II to the iron). Bair = Hair From the above cases it is seen that the vertical shielding in Case 2 is unsatisfactory in that the iron becomes saturated. Consider again the iron in Cast L (Figo 6} . I'll ' I• <:.""' - 6 .. UCRL 1888 (a) ~ron =Jtole when hole is II to7, = Bair~ = Bhole (b) "1 =Btole when h~le is j_ to-/ (c) Binside hole= 2~ron~~~ 1 + 1 ;zr Therefore, magnetic shielding design criteria should include the following: · 1. Iron shielding mass large with respect to shielded mass. 2. An aperture in the iron shielding whose greater dimension is parallel to the magnetic field, (However, practical geometry dictates circular or elliptical openings). 3. A liner of additional shielding material can be included within these apertures. SYMBO!S ~ H = magnetic field intensity ~=magnetic flux density i or I = current J2 or L = length C = constant f = constant ~ = permeability R = resistance R' = reluctance -'L= magnetomotive force A = area d"'= conductivity N = flux (total) n = turns MMF = magnetomotive force .
Load more

Recommended publications
  • On the First Electromagnetic Measurement of the Velocity of Light by Wilhelm Weber and Rudolf Kohlrausch
    Andre Koch Torres Assis On the First Electromagnetic Measurement of the Velocity of Light by Wilhelm Weber and Rudolf Kohlrausch Abstract The electrostatic, electrodynamic and electromagnetic systems of units utilized during last century by Ampère, Gauss, Weber, Maxwell and all the others are analyzed. It is shown how the constant c was introduced in physics by Weber's force of 1846. It is shown that it has the unit of velocity and is the ratio of the electromagnetic and electrostatic units of charge. Weber and Kohlrausch's experiment of 1855 to determine c is quoted, emphasizing that they were the first to measure this quantity and obtained the same value as that of light velocity in vacuum. It is shown how Kirchhoff in 1857 and Weber (1857-64) independently of one another obtained the fact that an electromagnetic signal propagates at light velocity along a thin wire of negligible resistivity. They obtained the telegraphy equation utilizing Weber’s action at a distance force. This was accomplished before the development of Maxwell’s electromagnetic theory of light and before Heaviside’s work. 1. Introduction In this work the introduction of the constant c in electromagnetism by Wilhelm Weber in 1846 is analyzed. It is the ratio of electromagnetic and electrostatic units of charge, one of the most fundamental constants of nature. The meaning of this constant is discussed, the first measurement performed by Weber and Kohlrausch in 1855, and the derivation of the telegraphy equation by Kirchhoff and Weber in 1857. Initially the basic systems of units utilized during last century for describing electromagnetic quantities is presented, along with a short review of Weber’s electrodynamics.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • The Meaning of the Constant C in Weber's Electrodynamics
    Proe. Int. conf. "Galileo Back in Italy - II" (Soc. Ed. Androme-:ia, Bologna, 2000), pp. 23-36, R. Monti (editor) The Meaning of the Constant c in Weber's Electrodynamics A. K. T. Assis' Instituto de Fisica 'Gleb Wat.aghin' Universidade Estadual de Campinas - Unicamp 13083-970 Campinas, Sao Paulo, Brasil Abstract In this work it is analysed three basic electromagnetic systems of units utilized during last century by Ampere, Gauss, Weber, Maxwell and all the others: The electrostatic, electrodynamic and electromagnetic ones. It is presented how the basic equations of electromagnetism are written in these systems (and also in the present day international system of units MKSA). Then it is shown how the constant c was introduced in physics by Weber's force. It is shown that it has the unit of velocity and is the ratio of the electromagnetic and electrostatic Wlits of charge. Weber and Kohlrausch '5 experiment to determine c is presented, emphasizing that they were 'the first to measure this quantity and obtained the same value as that of light velocity in vacuum. It is shown how Kirchhoff and Weber obtained independently of one another, both working in the framev.-ork of \Veber's electrodynamics, the fact that an electromagnetic signal (of current or potential) propagate at light velocity along a thin wire of negligible resistivity. Key Words: Electromagnetic units, light velocity, wave equation. PACS: O1.55.+b (General physics), 01.65.+g (History of science), 41.20.·q (Electric, magnetic, and electromagnetic fields) ·E-mail: assisOiCLunicamp.br, homepage: www.lCi.unicamp.brrassis AA. VV•.
    [Show full text]
  • Relationships of the SI Derived Units with Special Names and Symbols and the SI Base Units
    Relationships of the SI derived units with special names and symbols and the SI base units Derived units SI BASE UNITS without special SI DERIVED UNITS WITH SPECIAL NAMES AND SYMBOLS names Solid lines indicate multiplication, broken lines indicate division kilogram kg newton (kg·m/s2) pascal (N/m2) gray (J/kg) sievert (J/kg) 3 N Pa Gy Sv MASS m FORCE PRESSURE, ABSORBED DOSE VOLUME STRESS DOSE EQUIVALENT meter m 2 m joule (N·m) watt (J/s) becquerel (1/s) hertz (1/s) LENGTH J W Bq Hz AREA ENERGY, WORK, POWER, ACTIVITY FREQUENCY second QUANTITY OF HEAT HEAT FLOW RATE (OF A RADIONUCLIDE) s m/s TIME VELOCITY katal (mol/s) weber (V·s) henry (Wb/A) tesla (Wb/m2) kat Wb H T 2 mole m/s CATALYTIC MAGNETIC INDUCTANCE MAGNETIC mol ACTIVITY FLUX FLUX DENSITY ACCELERATION AMOUNT OF SUBSTANCE coulomb (A·s) volt (W/A) C V ampere A ELECTRIC POTENTIAL, CHARGE ELECTROMOTIVE ELECTRIC CURRENT FORCE degree (K) farad (C/V) ohm (V/A) siemens (1/W) kelvin Celsius °C F W S K CELSIUS CAPACITANCE RESISTANCE CONDUCTANCE THERMODYNAMIC TEMPERATURE TEMPERATURE t/°C = T /K – 273.15 candela 2 steradian radian cd lux (lm/m ) lumen (cd·sr) 2 2 (m/m = 1) lx lm sr (m /m = 1) rad LUMINOUS INTENSITY ILLUMINANCE LUMINOUS SOLID ANGLE PLANE ANGLE FLUX The diagram above shows graphically how the 22 SI derived units with special names and symbols are related to the seven SI base units. In the first column, the symbols of the SI base units are shown in rectangles, with the name of the unit shown toward the upper left of the rectangle and the name of the associated base quantity shown in italic type below the rectangle.
    [Show full text]
  • Mechanical Energy
    Chapter 2 Mechanical Energy Mechanics is the branch of physics that deals with the motion of objects and the forces that affect that motion. Mechanical energy is similarly any form of energy that’s directly associated with motion or with a force. Kinetic energy is one form of mechanical energy. In this course we’ll also deal with two other types of mechanical energy: gravitational energy,associated with the force of gravity,and elastic energy, associated with the force exerted by a spring or some other object that is stretched or compressed. In this chapter I’ll introduce the formulas for all three types of mechanical energy,starting with gravitational energy. Gravitational Energy An object’s gravitational energy depends on how high it is,and also on its weight. Specifically,the gravitational energy is the product of weight times height: Gravitational energy = (weight) × (height). (2.1) For example,if you lift a brick two feet off the ground,you’ve given it twice as much gravitational energy as if you lift it only one foot,because of the greater height. On the other hand,a brick has more gravitational energy than a marble lifted to the same height,because of the brick’s greater weight. Weight,in the scientific sense of the word,is a measure of the force that gravity exerts on an object,pulling it downward. Equivalently,the weight of an object is the amount of force that you must exert to hold the object up,balancing the downward force of gravity. Weight is not the same thing as mass,which is a measure of the amount of “stuff” in an object.
    [Show full text]
  • Weber's Law and Mach's Principle
    Weber's Law and Mach's Principle Andre K. T. Assis 1. Introduction Recently we applied a Weber's force law for gravitation to implement quantitatively Mach's Principle (Assis 1989, 1992a). In this work we present a briefreview of Weher's electrodynamics and analyze in greater detail the compliance of a Weber's force law for gravitation with Mach's Principle. 2. Weber's Electrodynamics In this section we discuss Weber's original work as applied to electro­ magnetism. For detailed references of Weber's electrodynamics, see (Assis 1992b, 1994). In order to unify electrostatics (Coulomb's force, Gauss's law) with electrodynamics (Ampere's force between current elements), W. Weber proposed in 1846 that the force exerted by an electrical charge q2 on another ql should be given by (using vectorial notation and in the International System of Units): (1) In this equation, (;0=8.85'10- 12 Flm is the permittivity of free space; the position vectors of ql and qz are r 1 and r 2, respectively; the distance between the charges is r lZ == Ir l - rzl '" [(Xl -XJ2 + (yj -yJZ + (Zl -ZJ2j112; r12=(r) -r;JlrI2 is the unit vector pointing from q2 to ql; the radial velocity between the charges is given by fIZ==drlzfdt=rI2'vIZ; and the Einstein Studies, vol. 6: Mach's Principle: From Newton's Bucket to Quantum Gravity, pp. 159-171 © 1995 Birkhliuser Boston, Inc. Printed in the United States. 160 Andre K. T. Assis radial acceleration between the charges is [VIZ" VIZ - (riZ "VIZ)2 + r lz " a 12J r" where drlz dvlz dTI2 rIZ=rl-rl , V1l = Tt' a'l=Tt= dt2· Moreover, C=(Eo J4J)"'!12 is the ratio of electromagnetic and electrostatic units of charge %=41f·1O-7 N/Al is the permeability of free space).
    [Show full text]
  • The International System of Units (SI)
    NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303.
    [Show full text]
  • WEBER Solutions 6
    WEBER Automatic Screwdriving Systems Technology That Connects www.weber-online.com 2 WEBER Automatic Screwdriving Systems | Contents Contents WEBER Expertise 5 WEBER Solutions 6 The “WEBER Principle” 8 Handheld Screwdriving 10 Fixtured Screwdriving Systems 14 Insertion Systems 18 Feeding Systems 20 Control Systems 22 Screwdriving Strategies 25 System Solutions 26 Service 34 WEBER Worldwide 38 3 The art of doing the right thing at the right moment High-end WEBER products set the standard for screwdriving automation 60 years after the company's foundation, the same principles still apply; each application is unique, each customer has specific requirements and each automation process requires a tailor-made solution. So when you ask what is the secret of WEBER's success, the answer is that we listen to the customer, carefully analyse the problem to be solved, develop alternatives, and devise an optimal solution in collaboration with the customer. And ultimately, it is all about increasing efficiency, optimising processes and helping our customers to be economically successful in business. We recognise that the needs of a medium-sized furniture assembly company are completely different from those of an automotive manufacturer. The quality of our products, solutions, and service is therefore measured primarily against our innovative automatic screwdriving systems, which have been leading the market since 1956. For me, the value of our company also lies in the fact that we speak the same language as our customers. This is why we want to show you on the following pages where we specialise and how you can benefit from our expertise. So get ready – for WEBER and technology that connects.
    [Show full text]
  • A) B) C) D) 1. Which Is an SI Unit for Work Done on an Object? A) Kg•M/S
    1. Which is an SI unit for work done on an object? 10. Which is an acceptable unit for impulse? A) B) A) N•m B) J/s C) J•s D) kg•m/s C) D) 11. Using dimensional analysis, show that the expression has the same units as acceleration. [Show all the 2. Which combination of fundamental units can be used to express energy? steps used to arrive at your answer.] A) kg•m/s B) kg•m2/s 12. Which quantity and unit are correctly paired? 2 2 2 C) kg•m/s D) kg•m /s A) 3. A joule is equivalent to a B) A) N•m B) N•s C) N/m D) N/s C) 4. A force of 1 newton is equivalent to 1 A) B) D) C) D) 13. Which two quantities are measured in the same units? 5. Which two quantities can be expressed using the same A) mechanical energy and heat units? B) energy and power A) energy and force C) momentum and work B) impulse and force D) work and power C) momentum and energy 14. Which is a derived unit? D) impulse and momentum A) meter B) second 6. Which pair of quantities can be expressed using the same C) kilogram D) Newton units? 15. Which combination of fundamental unit can be used to A) work and kinetic energy express the weight of an object? B) power and momentum A) kilogram/second C) impulse and potential energy B) kilogram•meter D) acceleration and weight C) kilogram•meter/second 7.
    [Show full text]
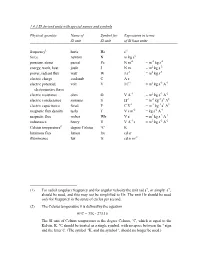
  • 1.4.3 SI Derived Units with Special Names and Symbols
    1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
  • Tones (Sounds) Loudness Surface: the Weber' Law for Hearing
    International Conference on Circuits and Systems (CAS 2015) Tones (Sounds) Loudness Surface: the Weber’ Law for Hearing Ovchinnikov Evgeny L Department of Medical and Biological Physics, Samara State Medical University, Samara, Russia Abstract—Purpose: Research and theoretical substantiation of In practice, the tone's loudness as a response to stimulation the hearing Weber law for sounds arbitrary frequencies and (sensation) is evaluated the decibel loudness, equating to intensities. declaratively on the standard frequency decibel intensity Objects: Results of classic psychophysical experiments of and decibel loudness, calling his phon.For arbitrary Weber, hearing Fechner model (equation) as a special case of frequencies and intensities of sound the Weber - Fechner the Weber law. law determined only experimentally and graphically is Methods: Audiometric for determining hearing acuity, displayed as the curves of equal loudness – isophon. But it biophysical for the substantiation of auditory process, methods can be shown that the differential equation represented by of mathematical analysis and computer simulation. Fechner as dЕ = k (dI/I), has a logical and a definite Results: To the analytical and graphical form is decision in the entire range of sound frequencies substantiated and submitted the hearing Weber law for arbitrary frequencies and intensities of sounds. permissible (comfortable) intensity. Experiments show that the auditory perception of a Keywords-sound (tones) loudness; loudness surface; weber’ sound, greater or smaller standard frequency, but the same law for hearing; sounds of arbitrary frequencies and intensities. loudness as the standard sound requires an increase in the intensity of the sound on the new frequency at this level. I. INTRODUCTION First let us identify the causes of this phenomenon – a Person's perception of sound energy (intensity I or nature of tones (sounds) of equal loudness.
    [Show full text]