DOCSLIB.ORG

Capacitor in RC Circuits

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Capacitor in RC Circuits Lecture 11 – 1/18 Capacitor in RC Circuits I I charging discharging • Switch closed at t=0 • Switch closed at t=0 • Initial • Initial ▪ Capacitor (C) initially ▪ Capacitor (C) initially charged uncharged ▪ V = Q /C across C ▪ 0 0 V0 = 0 across C ▪ I = V /R ▪ I = Emf/R 0 0 0 • Final (after a long time) • Final (after a long time) ▪ Capacitor (C) fully discharged ▪ Capacitor (C) fully charged ▪ V∞ = 0 across C ▪ V∞ = Emf across C ▪ I∞ = 0 ▪ I∞ = 0 Lecture 11 – 2/18 Discharging a Capacitor in RC Circuits 1. Switch closed at t=0. Initially C is fully charged with Q0 Q 2. Loop Rule: I R 0 C 3. Convert to a differential equation dQ Q dQ I I R 0 dt C dt 4. Solve it! t dQ dt RC Q RC Q Q0 e t Q t dQ Q0 RC ln I e RC is the time dt RC constant (τ) Q0 RC Lecture 11 – 3/18 Charge Q(t) during Discharging • Charge on the capacitor as a function of time: t / RC t / Q(t) Q0 e Q0 e units of the time ▪ Q0 is the initial charge constant (τ) are seconds C C [ ] [RC] s time constant V A Charge after time τ 0.37 Q0 is given by: 1 Q( ) Q0 e 0.37Q0 Lecture 11 – 4/18 Current I(t) during Discharging t / Starting with Q(t) Q0 e • Current from the capacitor dQ as a function of time: I dt t / I(t) I0 e Q0 t / t / I e I0 e ▪ I0 is the initial current Q Q V I 0 0 0 0 RC R Charge after time τ is given by: 1 I( ) I0 e 0.37 I0 Lecture 11 – 5/18 Charging a Capacitor in RC Circuits 1. Switch closed at t=0. Initially C is uncharged with V=0 Q 2. Loop Rule: I R 0 C 3. Convert to a differential equation dQ Q dQ I R 0 dt C dt 4. Solve it! t t Q C 1e RC Q 1e RC f t t RC is the time dQ I e RC I e RC constant (τ) dt R 0 Lecture 11 – 6/18 Charge Q(t) during Charging • Charge on the capacitor as a function of time: t / RC t / Q(t) C (1e ) Q f (1 e ) ▪ Qf is the final charge Qf CV Charge after time τ is given by: time constant 1 Q( ) Qf (1e ) Q( ) 0.63Qf Lecture 11 – 7/18 Current I(t) during Charging Q(t) Q (1et / ) Starting with f • Current to the capacitor dQ as a function of time: I dt t / I(t) I0 e Qf t / t / I e I0 e ▪ I0 is the initial current Q Q I f f 0 RC R Charge after time τ is given by: 0.37 I0 1 I( ) I0 e 0.37 I0 Lecture 11 – 8/18 Capacitor Equations • Which equation is for charging and which is discharging? t / t / Q(t) Q0 e Q(t) Q f (1 e ) Discharging Charging • Check the charge on the capacitor initially (at t=0) 0/ Q(0) Q (1 e0/ ) Q(0) Q0 e f 0 Q(0) Q (1 e0 ) Q(0) Q0 e f Q(0) Q0 (1) Q(0) Q f (11) Q(0) Q0 Q(0) 0 Initially has charge Q0 Initially has zero charge Lecture 11 – 9/18 Quiz Question 1 Which curve best represents the charge on the capacitor in a charging RC circuit as a function of time? Lecture 11 – 10/18 Quiz Question 2 What’s the time constant in the following circuit. All resistors have the same resistance R, and all capacitors have the same capacitance C. R R a) (3/5)RC b) 2RC R c) RC C C d) (4/9)RC V e) (6/4)RC S C Lecture 11 – 11/18 Behavior of Capacitors in Circuits • Charging ▪ Initially, the capacitor behaves like a wire ▪ After a long time, the capacitor behaves like an open switch • Discharging ▪ Initially, the capacitor behaves like a battery ▪ After a long time, the capacitor behaves like an open switch Lecture 11 – 12/18 Example of a More Complex Circuit R2 • Switch S is open for a long I2 time and then closed. I1 I R1 3 Junction Rule: I I I R3 1 2 3 C •What is the initial current? V (when S is just closed) R S eq12 Q Loop Rule: V I R 0 0 eq12 C V R3 C V I0 (R1 R2 ) 0 0 V I0 I3 0 I1 I2 I0 R1 R2 Lecture 11 – 13/18 Example of a More Complex Circuit R2 • Switch S is open for a long I2 time and then closed. I1 I R1 3 Junction Rule: I I I R3 1 2 3 C •What is the final current? V (when S closed for long time) S Req12 Loop Rule: V I f Req12 I f R3 0 V R3 C V I f (R1 R2 R3 ) 0 V I f I2 0 I1 I3 I f R1 R2 R3 Lecture 11 – 14/18 Example of a More Complex Circuit R2 • Switch S is closed for a long I2 time and then opened. I1 I Junction Rule: R1 R 3 I I I 3 •What is the initial1 current2 3? C V (when S is just opened) R eq12 S Loop Rule: VC I0, S opened R3 0 V R3 C I f R3 I0, S opened R3 0 V I0, S opened I f I1 0 I2 I3 I0, S opened R1 R2 R3 • What is the final current? I 0 (when S is open f , S opened for long time) Lecture 11 – 15/18 Quiz Question 3 A RC circuit consists of a battery with potential V = 100 V, a resistor with R = 10 Ω, and a capacitor with C = 14 μF R V C S A) I0 = 10 A If = 0 A D) I0 = 25 A If = 3 A B) I0 = 15 A If = 2 A E) I0 = 3 A If = 25 A C) I0 = 0 A If = 10 A Lecture 11 – 16/18 Quiz Question 4 The switch S is initially at position a for a long time. It is then switched to position b. Describe what happens to the light bulb as a function of time after the switch is a bulb flipped from a to b. S b V C a) The light bulb goes on but goes off immediately. b) The light bulb goes off and stays off. c) The light bulb goes on but its brightness decreases with time and eventually goes off. d) The light bulb goes on and stays on at a constant brightness. e) The light bulb goes on but its brightness increases with time. Lecture 11 – 17/18 Energy Conservation in Discharging a Capacitor • Discharging: Energy lost by capacitor (C) 1 1 U Q V CV 2 2 0 0 2 0 Power dissipated by resistor (R) dW P I(t)2 R I 2e2t / R R dt 0 Total Energy dissipated by resistor (R) W P (t) dt I 2 R e2t / dt R R 0 Energy Conservation 0 0 U W 2 2 R 2 V0 R C 1 2 WR I0 R CV0 2 R 2 2 Lecture 11 – 18/18 Energy Conservation in Charging a Capacitor • Charging: Energy stored in capacitor (C) Work done by 1 1 U Q V CV 2 battery (V) 2 f 2 2 W Q f V CV Power dissipated by resistor (R) dW P I(t)2 R I 2e2t / R R dt 0 Total Energy dissipated by resistor (R) W P (t) dt I 2 R e2t / dt R R 0 0 0 2 2 2 V R C 1 2 WR I0 R CV Independent of R 2 R 2 2.
Load more

Recommended publications
  • Electrical Circuits Lab. 0903219 Series RC Circuit Phasor Diagram
    Electrical Circuits Lab. 0903219 Series RC Circuit Phasor Diagram - Simple steps to draw phasor diagram of a series RC circuit without memorizing: * Start with the quantity (voltage or current) that is common for the resistor R and the capacitor C, which is here the source current I (because it passes through both R and C without being divided). Figure (1) Series RC circuit * Now we know that I and resistor voltage VR are in phase or have the same phase angle (there zero crossings are the same on the time axis) and VR is greater than I in magnitude. * Since I equal the capacitor current IC and we know that IC leads the capacitor voltage VC by 90 degrees, we will add VC on the phasor diagram as follows: * Now, the source voltage VS equals the vector summation of VR and VC: Figure (2) Series RC circuit Phasor Diagram Prepared by: Eng. Wiam Anabousi - Important notes on the phasor diagram of series RC circuit shown in figure (2): A- All the vectors are rotating in the same angular speed ω. B- This circuit acts as a capacitive circuit and I leads VS by a phase shift of Ө (which is the current angle if the source voltage is the reference signal). Ө ranges from 0o to 90o (0o < Ө <90o). If Ө=0o then this circuit becomes a resistive circuit and if Ө=90o then the circuit becomes a pure capacitive circuit. C- The phase shift between the source voltage and its current Ө is important and you have two ways to find its value: a- b- = - = - D- Using the phasor diagram, you can find all needed quantities in the circuit like all the voltages magnitude and phase and all the currents magnitude and phase.
    [Show full text]
  • Phasor Analysis of Circuits
    Phasor Analysis of Circuits Concepts Frequency-domain analysis of a circuit is useful in understanding how a single-frequency wave undergoes an amplitude change and phase shift upon passage through the circuit. The concept of impedance or reactance is central to frequency-domain analysis. For a resistor, the impedance is Z ω = R , a real quantity independent of frequency. For capacitors and R ( ) inductors, the impedances are Z ω = − i ωC and Z ω = iω L. In the complex plane C ( ) L ( ) these impedances are represented as the phasors shown below. Im ivL R Re -i/vC These phasors are useful because the voltage across each circuit element is related to the current through the equation V = I Z . For a series circuit where the same current flows through each element, the voltages across each element are proportional to the impedance across that element. Phasor Analysis of the RC Circuit R V V in Z in Vout R C V ZC out The behavior of this RC circuit can be analyzed by treating it as the voltage divider shown at right. The output voltage is then V Z −i ωC out = C = . V Z Z i C R in C + R − ω + The amplitude is then V −i 1 1 out = = = , V −i +ω RC 1+ iω ω 2 in c 1+ ω ω ( c ) 1 where we have defined the corner, or 3dB, frequency as 1 ω = . c RC The phasor picture is useful to determine the phase shift and also to verify low and high frequency behavior. The input voltage is across both the resistor and the capacitor, so it is equal to the vector sum of the resistor and capacitor voltages, while the output voltage is only the voltage across capacitor.
    [Show full text]
  • 5 RC Circuits
    Physics 212 Lab Lab 5 RC Circuits What You Need To Know: The Physics In the previous two labs you’ve dealt strictly with resistors. In today’s lab you’ll be using a new circuit element called a capacitor. A capacitor consists of two small metal plates that are separated by a small distance. This is evident in a capacitor’s circuit diagram symbol, see Figure 1. When a capacitor is hooked up to a circuit, charges will accumulate on the plates. Positive charge will accumulate on one plate and negative will accumulate on the other. The amount of charge that can accumulate is partially dependent upon the capacitor’s capacitance, C. With a charge distribution like this (i.e. plates of charge), a uniform electric field will be created between the plates. [You may remember this situation from the Equipotential Surfaces lab. In the lab, you had set-ups for two point-charges and two lines of charge. The latter set-up represents a capacitor.] A main function of a capacitor is to store energy. It stores its energy in the electric field between the plates. Battery Capacitor (with R charges shown) C FIGURE 1 - Battery/Capacitor FIGURE 2 - RC Circuit If you hook up a battery to a capacitor, like in Figure 1, positive charge will accumulate on the side that matches to the positive side of the battery and vice versa. When the capacitor is fully charged, the voltage across the capacitor will be equal to the voltage across the battery. You know this to be true because Kirchhoff’s Loop Law must always be true.
    [Show full text]
  • ELECTRICAL CIRCUIT ANALYSIS Lecture Notes
    ELECTRICAL CIRCUIT ANALYSIS Lecture Notes (2020-21) Prepared By S.RAKESH Assistant Professor, Department of EEE Department of Electrical & Electronics Engineering Malla Reddy College of Engineering & Technology Maisammaguda, Dhullapally, Secunderabad-500100 B.Tech (EEE) R-18 MALLA REDDY COLLEGE OF ENGINEERING AND TECHNOLOGY II Year B.Tech EEE-I Sem L T/P/D C 3 -/-/- 3 (R18A0206) ELECTRICAL CIRCUIT ANALYSIS COURSE OBJECTIVES: This course introduces the analysis of transients in electrical systems, to understand three phase circuits, to evaluate network parameters of given electrical network, to draw the locus diagrams and to know about the networkfunctions To prepare the students to have a basic knowledge in the analysis of ElectricNetworks UNIT-I D.C TRANSIENT ANALYSIS: Transient response of R-L, R-C, R-L-C circuits (Series and parallel combinations) for D.C. excitations, Initial conditions, Solution using differential equation and Laplace transform method. UNIT - II A.C TRANSIENT ANALYSIS: Transient response of R-L, R-C, R-L-C Series circuits for sinusoidal excitations, Initial conditions, Solution using differential equation and Laplace transform method. UNIT - III THREE PHASE CIRCUITS: Phase sequence, Star and delta connection, Relation between line and phase voltages and currents in balanced systems, Analysis of balanced and Unbalanced three phase circuits UNIT – IV LOCUS DIAGRAMS & RESONANCE: Series and Parallel combination of R-L, R-C and R-L-C circuits with variation of various parameters.Resonance for series and parallel circuits, concept of band width and Q factor. UNIT - V NETWORK PARAMETERS:Two port network parameters – Z,Y, ABCD and hybrid parameters.Condition for reciprocity and symmetry.Conversion of one parameter to other, Interconnection of Two port networks in series, parallel and cascaded configuration and image parameters.
    [Show full text]
  • How to Design Analog Filter Circuits.Pdf
    a b FIG. 1-TWO LOWPASS FILTERS. Even though the filters use different components, they perform in a similiar fashion. MANNlE HOROWITZ Because almost every analog circuit contains some filters, understandinghow to work with them is important. Here we'll discuss the basics of both active and passive types. THE MAIN PURPOSE OF AN ANALOG FILTER In addition to bandpass and band- age (because inductors can be expensive circuit is to either pass or reject signals rejection filters, circuits can be designed and hard to find); they are generally easier based on their frequency. There are many to only pass frequencies that are either to tune; they can provide gain (and thus types of frequency-selective filter cir- above or below a certain cutoff frequency. they do not necessarily have any insertion cuits; their action can usually be de- If the circuit passes only frequencies that loss); they have a high input impedance, termined from their names. For example, are below the cutoff, the circuit is called a and have a low output impedance. a band-rejection filter will pass all fre- lo~~passfilter, while a circuit that passes A filter can be in a circuit with active quencies except those in a specific band. those frequencies above the cutoff is a devices and still not be an active filter. Consider what happens if a parallel re- higlzpass filter. For example, if a resonant circuit is con- sonant circuit is connected in series with a All of the different filters fall into one . nected in series with two active devices signal source.
    [Show full text]
  • The RC Circuit
    The RC Circuit The RC Circuit Pre-lab questions 1. What is the meaning of the time constant, RC? 2. Show that RC has units of time. 3. Why isn’t the time constant defined to be the time it takes the capacitor to become fully charged or discharged? 4. Explain conceptually why the time constant is larger for increased resistance. 5. What does an oscilloscope measure? 6. Why can’t we use a multimeter to measure the voltage in the second half of this lab? 7. Draw and label a graph that shows the voltage across a capacitor that is charging and discharging (as in this experiment). 8. Set up a data table for part one. (V, t (0-300s in 20s intervals, 360, and 420s)) Introduction The goal in this lab is to observe the time-varying voltages in several simple circuits involving a capacitor and resistor. In the first part, you will use very simple tools to measure the voltage as a function of time: a multimeter and a stopwatch. Your lab write-up will deal primarily with data taken in this part. In the second part of the lab, you will use an oscilloscope, a much more sophisticated and powerful laboratory instrument, to observe time behavior of an RC circuit on a much faster timescale. Your observations in this part will be mostly qualitative, although you will be asked to make several rough measurements using the oscilloscope. Part 1. Capacitor Discharging Through a Resistor You will measure the voltage across a capacitor as a function of time as the capacitor discharges through a resistor.
    [Show full text]
  • Capacitors, Inductors, and First-Order Linear Circuits Overview
    EECE251 Circuit Analysis I Set 4: Capacitors, Inductors, and First-Order Linear Circuits Shahriar Mirabbasi Department of Electrical and Computer Engineering University of British Columbia [email protected] SM 1 EECE 251, Set 4 Overview • Passive elements that we have seen so far: resistors. We will look into two other types of passive components, namely capacitors and inductors. • We have already seen different methods to analyze circuits containing sources and resistive elements. • We will examine circuits that contain two different types of passive elements namely resistors and one (equivalent) capacitor (RC circuits) or resistors and one (equivalent) inductor (RL circuits) • Similar to circuits whose passive elements are all resistive, one can analyze RC or RL circuits by applying KVL and/or KCL. We will see whether the analysis of RC or RL circuits is any different! Note: Some of the figures in this slide set are taken from (R. Decarlo and P.-M. Lin, Linear Circuit Analysis , 2nd Edition, 2001, Oxford University Press) and (C.K. Alexander and M.N.O Sadiku, Fundamentals of Electric Circuits , 4th Edition, 2008, McGraw Hill) SM 2 EECE 251, Set 4 1 Reading Material • Chapters 6 and 7 of the textbook – Section 6.1: Capacitors – Section 6.2: Inductors – Section 6.3: Capacitor and Inductor Combinations – Section 6.5: Application Examples – Section 7.2: First-Order Circuits • Reading assignment: – Review Section 7.4: Application Examples (7.12, 7.13, and 7.14) SM 3 EECE 251, Set 4 Capacitors • A capacitor is a circuit component that consists of two conductive plate separated by an insulator (or dielectric).
    [Show full text]
  • Inductors and Capacitors in AC Circuits
    Inductors and Capacitors in AC Circuits IMPORTANT NOTE: A USB flash drive is needed for the first section of this lab. Make sure to bring one with you! Introduction The goal of this lab is to look at the behaviour of inductors and capacitors - two circuit components which may be new to you. In AC circuits currents vary in time, therefore we have to consider variations in the energy stored in electric and magnetic fields of capacitors and inductors, respectively. You are already familiar with resistors, where the voltage-current relation is given by Ohm's law: VR(t) = RI(t); (1) In an inductor, the voltage is proportional to the rate of change of the current. You may recall the example of a coil of wire, where changing the current changes the magnetic flux, creating a voltage in the opposite direction (Lenz's law). A capacitor is a component where a charge difference builds up across the component. A simple example of this is a pair of parallel plates separated by a small distance, with a charge difference between them. The potential difference between the plates depends on the charge difference Q, which can also be written as the integral over time of the current flowing into/out of the capacitor. Inductors and capacitors are characterized by their inductance L and capacitance C respectively, with the voltage difference across them given by dI(t) V (t) = L ; (2) L dt Z t Q(t) 1 0 0 VC (t) = = I(t )dt (3) C C 0 1 Transient Behaviour In this first section, we'll look at how circuits with these components behave when an applied DC voltage is switched from one value to another.
    [Show full text]
  • Switched Capacitor Networks and Techniques for the Period 19 1-1992
    Active and Passive Elec. Comp., 1994, Vol. 16, pp. 171-258 Reprints available directly from the publisher Photocopying permitted by license only 1994 Gordon and Breach Science Publishers S.A. Printed in Malaysia A CHRONOLOGICAL LIST OF REFERENCES ON SWITCHED CAPACITOR NETWORKS AND TECHNIQUES FOR THE PERIOD 19 1-1992 A.K. SINGH Electronics Lab., Department of Electronics and Communication Engineering, Delhi Institute of Technology, Kashmere Gate, Delhi 110006, India. (Received November 16, 1993; in final form December 15, 1993) A chronological list of 440 references on switched capacitor (SC) networks from 1939 to May 1981 was published in this Journal by J. Vandewalle. In this communication, we present a compilation of 1357 references covering the period from May 1981-1992 (along with a supplementary list of 43 missing references for the period before May 1981). The present compilation and the earlier one by Vandewalle put together, thus, constitute an exhaustive bibliography of 1797 references on SC-networks and tech- niques till 1992. I. INTRODUCTION The importance of SC-networks in the area of instrumentation and communication is well established. Because of their suitability to VLSI implementation, along with digital networks on the same chip and their low cost coupled with accuracy, SC- networks have greatly enhanced their applicability in the electronics world. Enor- mous volumes of literature on the SC-techniques for different applications is now available. Many design procedures including those based upon immittance simu- lation and wave concepts have been evolved. Application of SC-networks in the design of FIR and IIR filters and neural networks have also been reported.
    [Show full text]
  • Last Time: LRC Circuits with Phasors…
    Last time: LRC Circuits with phasors… I X where . R L εm XLL ≡ ω C L ⇒ φ IR 1 ∼ X C ≡ I XC ωC ε The phasor diagram gives us graphical solutions for φ and I: 2 2 2 2 ε=IRXXm ( +( LC − ) ) I XL I XC εm ⇓ φ 2 2 XX− I=ε m R + X()LC − X = IZ IR tanφ = LC R 2 2 ZRXX≡ +()LC − LRC series circuit; Summary of instantaneous Current and voltages VR = IR VL = IXL VC = IXC i t()= Icos (ω ) t I XL vR t()= IRcos (ω ) t ε 1 m v t()= IXcos (ω− t ) 90 = cos I ()ωt − 90 C C ωC v tL ()= IXcosL (ω+ t ) 90ω = cos I L( ω+ ) 90 t IR tε()= v t() = ω IZcos (+ φ ) t = εcos (t ω+ ) φ ad m I XC VVLC− ωLC−1 / ω 2 2 tanφ = = ZXXX=(()R + LC - ) VR R Lagging & Leading The phase φ between the current and the driving emf depends on the relative magnitudes of the inductive and capacitive reactances. XL≡ ω ε XXLC− L m tan φ = I = 1 Z R X ≡ C ω C XL Z XL XL φ Z R φ R R Z XC XC XC XL > XC XL < XC XL = XC φ > 0 φ < 0 φ = 0 current current current LAGS LEADS IN PHASE WITH applied voltage applied voltage applied voltage Lecture 19, Act 2 2A A series RC circuit is driven by emf ε. Which of the following could be an appropriate phasor ~ diagram? V ε L εm m VC VR VR VR V C εm VC (a) (b) (c) 2B For this circuit which of the following is true? (a) The drive voltage is in phase with the current.
    [Show full text]
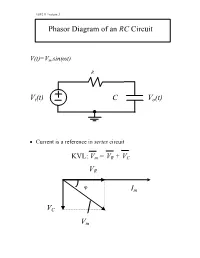
  • Phasor Diagram of an RC Circuit Vi(T) C Vo(T) VR Vm Im VC
    ESE211 Lecture 3 Phasor Diagram of an RC Circuit V(t)=Vm sin(ωt) R Vi(t) C Vo(t) • Current is a reference in series circuit KVL: Vm = VR + VC V R ϕ Im VC V m ESE211 Lecture 3 Phasor Diagram of an RL Circuit V(t)=Vmsin(ωt) VR (t) R Vi(t) L Vo(t) KVL: Vm = VR + VL Vm VL ϕ VR Im ESE211 Lecture 3 Phasor Diagram of a Series RLC Circuit VC VL C L Vi R VR KVL: Vm = VC + VL + VR VL Vm VL-C VR Im VC • Voltages across capacitor and inductor compensate each other ESE211 Lecture 4 Integrating Circuit VR Vi(t) R Vo(t) C 22 VViR=+VC or VViR=+VC • Assume high frequency 1/ωC << R then VR >> VC VVRi≈ 11t t VOi=≈Idt Vdi t ∫∫ C 00RC Vi VV∝ dt Oi∫ • Accurate integrating can be obtained at high frequency that leads to a low output signal ESE211 Lecture 4 Differentiating Circuit VC Vi(t) C Vo(t) R 22 VViR=+VC or VViR=+VC • Assume low frequency 1/ωC >> R then VR << VC VR 1 t d Vii≈⇒Idt Iii=C V Vi VVCi≈ ∫ C 0 dt d VV==IR≈RCV ORi dt i d VOi∝ V dt • An accurate result can be achived at low frequency. ESE211 Lecture 4 Transient Processes in Passive Circuits RC Circuit without a Source • The circuit response is due only to the energy stored in the capacitor t=0 C R • The capacitor C is precharged to the voltage V0 Applying KCL: C dV/dt +V/R = 0 • This is the 1st order differential equation ESE211 Lecture 4 Solution of the Differential Equation dV/dt + V/RC = 0 dV/V = -dt/RC ln V = -t/RC +a V = A e -t/RC , A=e+a • e is the base of the natural logarithms, e = 2.718… • Continuity requires the initial condition: At t = 0 V(0) = V0 -t/RC V(t) = V0 e • The response governed
    [Show full text]
  • First Order Circuits
    First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance. So there are two types of first- order circuits: z RC circuit z RL circuit Source-Free Circuits A source-free circuit is one where all independent sources have been disconnected from the circuit after some switch action. The voltages and currents in the circuit typically will have some transient response due to initial conditions (initial capacitor voltages and initial inductor currents). We will begin by analyzing source-free circuits as they are the simplest type. Later we will analyze circuits that also contain sources after the initial switch action. SOURCE-FREE RC CIRCUITS z Consider the RC circuit shown below. Note that it is source-free because no sources are connected to the circuit for t > 0. Use KCL to find the differential equation: dv 1 t = 0 + += v(t) 0 for t ≥ 0 dt RC _+ VX R C v (t) z and solve the differential _ equation to show that: -t RC v(t) = VXe for t ≥ 0 SOURCE-FREE RC CIRCUITS Checks on the solution z Verify that the initial condition is satisfied. z Show that the energy dissipated over all time by the resistor equals the initial energy stored in the capacitor. First Order Circuits General form of the D.E. and the response for a 1st-order source-free circuit z In general, a first-order D.E. has the form: dx 1 += x(t) 0 for t ≥ 0 dt τ Solving this differential equation (as we did with the RC circuit) yields: -t
    [Show full text]