Lecture # 12 - Derivatives of Functions of Two Or More Vari- Ables (Cont.)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Using FXML in Javafx
JavaFX and FXML How to use FXML to define the components in a user interface. FXML FXML is an XML format text file that describes an interface for a JavaFX application. You can define components, layouts, styles, and properties in FXML instead of writing code. <GridPane fx:id="root" hgap="10.0" vgap="5.0" xmlns="..."> <children> <Label fx:id="topMessage" GridPane.halignment="CENTER"/> <TextField fx:id="inputField" width="80.0" /> <Button fx:id="submitButton" onAction="#handleGuess" /> <!-- more components --> </children> </GridPane> Creating a UI from FXML The FXMLLoader class reads an FXML file and creates a scene graph for the UI (not the window or Stage). It creates objects for Buttons, Labels, Panes, etc. and performs layout according to the fxml file. creates FXMLLoader reads game.fxml Code to Provide Behavior The FXML scene define components, layouts, and property values, but no behavior or event handlers. You write a Java class called a Controller to provide behavior, including event handlers: class GameController { private TextField inputField; private Button submitButton; /** event handler */ void handleGuess(ActionEvent e)... Connecting References to Objects The FXML scene contains objects for Button, TextField, ... The Controller contains references to the objects, and methods to supply behavior. How to Connect Objects to References? class GameController { private TextField inputField; private Button submitButton; /** event handler */ void handleGuess(ActionEvent e)... fx:id and @FXML In the FXML file, you assign objects an "fx:id". The fx:id is the name of a variable in the Controller class annotated with @FXML. You can annotate methods, too. fx:id="inputField" class GameController { @FXML private TextField inputField; @FXML private Button submitButton; /** event handler */ @FXML void handleGuess(ActionEvent e) The fxml "code" You can use ScaneBuilder to create the fxml file. -

Macroeconomic and Foreign Exchange Policies of Major Trading Partners of the United States
REPORT TO CONGRESS Macroeconomic and Foreign Exchange Policies of Major Trading Partners of the United States U.S. DEPARTMENT OF THE TREASURY OFFICE OF INTERNATIONAL AFFAIRS December 2020 Contents EXECUTIVE SUMMARY ......................................................................................................................... 1 SECTION 1: GLOBAL ECONOMIC AND EXTERNAL DEVELOPMENTS ................................... 12 U.S. ECONOMIC TRENDS .................................................................................................................................... 12 ECONOMIC DEVELOPMENTS IN SELECTED MAJOR TRADING PARTNERS ...................................................... 24 ENHANCED ANALYSIS UNDER THE 2015 ACT ................................................................................................ 48 SECTION 2: INTENSIFIED EVALUATION OF MAJOR TRADING PARTNERS ....................... 63 KEY CRITERIA ..................................................................................................................................................... 63 SUMMARY OF FINDINGS ..................................................................................................................................... 67 GLOSSARY OF KEY TERMS IN THE REPORT ............................................................................... 69 This Report reviews developments in international economic and exchange rate policies and is submitted pursuant to the Omnibus Trade and Competitiveness Act of 1988, 22 U.S.C. § 5305, and Section -

Differentiation Rules (Differential Calculus)
Differentiation Rules (Differential Calculus) 1. Notation The derivative of a function f with respect to one independent variable (usually x or t) is a function that will be denoted by D f . Note that f (x) and (D f )(x) are the values of these functions at x. 2. Alternate Notations for (D f )(x) d d f (x) d f 0 (1) For functions f in one variable, x, alternate notations are: Dx f (x), dx f (x), dx , dx (x), f (x), f (x). The “(x)” part might be dropped although technically this changes the meaning: f is the name of a function, dy 0 whereas f (x) is the value of it at x. If y = f (x), then Dxy, dx , y , etc. can be used. If the variable t represents time then Dt f can be written f˙. The differential, “d f ”, and the change in f ,“D f ”, are related to the derivative but have special meanings and are never used to indicate ordinary differentiation. dy 0 Historical note: Newton used y,˙ while Leibniz used dx . About a century later Lagrange introduced y and Arbogast introduced the operator notation D. 3. Domains The domain of D f is always a subset of the domain of f . The conventional domain of f , if f (x) is given by an algebraic expression, is all values of x for which the expression is defined and results in a real number. If f has the conventional domain, then D f usually, but not always, has conventional domain. Exceptions are noted below. -

TV CHANNEL LINEUP by Channel Name
TV CHANNEL LINEUP By Channel Name: 34: A&E 373: Encore Black 56: History 343: Showtime 2 834: A&E HD 473: Encore Black HD 856: History HD 443: Showtime 2 HD 50: Freeform 376: Encore Suspense 26: HLN 345: Showtime Beyond 850: Freeform HD 476: Encore Suspense 826: HLN HD 445: Showtime Beyond HD 324: ActionMax 377: Encore Westerns 6: HSN 341: Showtime 130: American Heroes Channel 477: Encore Westerns 23: Investigation Discovery 346: Showtime Extreme 930: American Heroes 35: ESPN 823: Investigation Discovery HD 446: Showtime Extreme HD Channel HD 36: ESPN Classic 79: Ion TV 348: Showtime Family Zone 58: Animal Planet 835: ESPN HD 879: Ion TV HD 340: Showtime HD 858: Animal Planet HD 38: ESPN2 2: Jewelry TV 344: Showtime Showcase 117: Boomerang 838: ESPN2 HD 10: KMIZ - ABC 444: Showtime Showcase HD 72: Bravo 37: ESPNews 810: KMIZ - ABC HD 447: Showtime Woman HD 872: Bravo HD 837: ESPNews HD 9: KMOS - PBS 347: Showtime Women 45: Cartoon Network 108: ESPNU 809: KMOS - PBS HD 22: Smile of a Child 845: Cartoon Network HD 908: ESPNU HD 5: KNLJ - IND 139: Sportsman Channel 18: Charge! 21: EWTN 7: KOMU - CW 939: Sportsman Channel HD 321: Cinemax East 62: Food Network 807: KOMU - CW HD 361: Starz 320: Cinemax HD 862: Food Network HD 8: KOMU - NBC 365: Starz Cinema 322: Cinemax West 133: Fox Business Network 808: KOMU - NBC HD 465: Starz Cinema HD 163: Classic Arts 933: Fox Business Network HD 11: KQFX - Fox 366: Starz Comedy 963: Classic Arts HD 48: Fox News Channel 811: KQFX - Fox HD 466: Starz Comedy HD 17: Comet 848: Fox News Channel HD 13: KRCG -

The FX Global Code
ALERT MEMORANDUM The FX Global Code July 6, 2017 On May 25, 2017, central banks, regulatory bodies, If you have any questions concerning market participants, and industry working groups from this memorandum, please reach out to your regular firm contact or the a range of jurisdictions released the FX Global Code following authors (the “Code”).1 The Code is a common set of principles intended to enhance the integrity and effective LONDON functioning of the wholesale foreign exchange markets Bob Penn (“FX markets”), certain segments of which have, to +44 20 7614 2277 [email protected] date, been largely unregulated. The Code will Anna Lewis-Martinez supplement, rather than replace, the legal and +44 20 7847 6823 regulatory obligations of adherents. [email protected] Although the Code includes principles that are akin to Christina Edward +44 20 7614 2201 many of the requirements under the new Markets in [email protected] Financial Instruments Directive package (“MiFID II”) and U.S. Commodity Futures Trading Commission NEW YORK Colin D. Lloyd (“CFTC”) rules under the Dodd-Frank Wall Street +1 212 225 2809 [email protected] Reform and Consumer Protection Act of 2010 (“Dodd-Frank Act”), in several respects the Code Brian Morris +1 212 225 2795 goes beyond those requirements. As such, for many [email protected] market participants, adherence to the Code will require Truc Doan material changes to existing operating models, +1 212 225 2305 compliance procedures, client disclosures, and other [email protected] documentation. Adherence to the Code is voluntary, but several regulators have expressed that they expect market participants to adhere, and there will be public and private sector pressure to publicize adherence. -
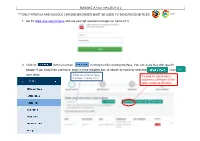
Sending a File Via Uso-Fx 2 ****Only Firefox and Google
SENDING A FILE VIA USO-FX 2 ****ONLY FIREFOX AND GOOGLE CHROME BROWSER MUST BE USED TO SEND/RECEIVE FILES **** 1. Go To https://my.uso.im/home and use your lgfl username to login (ie: name.211) 2. Click on (left menu) then to bring the files sharing interface. You can share files with specific people: if you know their username, enter it in the recipient box, or search by name by selecting . Click once done. Enter username here To look for users when if known (name.211) username unknown (it will open a pop up window) 3. You can enter a title and comment on the next screen (optional), click once done. 4. You can select files which are either stored on My Drive, but you will most commonly from your computer. Browse for the file you need and click . To upload files To select files from your computer stored on MyDrive 5. On the next screen, check that all details are correct and click .YOUR FILE HAS NOW BEEN SENT TO THE RECIPIENT. RECEIVING A FILE VIA USO-FX2 ****ONLY FIREFOX AND GOOGLE CHROME BROWSER MUST BE USED TO SEND/RECEIVE FILES **** 1. You will receive a notification email from atomwide in the following format: 2. Go To https://my.uso.im/home and use your lgfl username to login (ie: name.211) 3. Click on (left menu) and select . It will bring the received files interface where you can see all the files sent to you with the sender’s details, the type of file, when it was sent (uploaded) and the title and comments. -

Poweredge Fx2 Enclosure
POWEREDGE FX2 ENCLOSURE The Dell PowerEdge FX2 enclosure is the uniquely small modular foundation for the PowerEdge FX architecture, an extremely flexible and efficient platform for building an IT infrastructure that precisely fits your computing needs. The PowerEdge FX2 is a 2U hybrid rack-based computing platform Innovative management with intelligent automation that combines the density and efficiencies of blades with the The Dell OpenManage systems management portfolio simplifies and simplicity and cost benefits of rack-based systems. automates server lifecycle management — making IT operations Flexible configurations, more choice more efficient and Dell servers the most productive, reliable and cost The FX architecture’s innovative modular design supports IT resource effective. Dell’s agent-free integrated Dell Remote Access Controller building blocks of varying sizes (compute, storage, networking and (iDRAC) with Lifecycle Controller makes server deployment, management) so data centers have greater flexibility to construct configuration and updates automated and efficient. Using Chassis their infrastructures. The FX architecture includes the following Management Controller (CMC), an embedded component that is server nodes and storage block: part of every FX2 chassis, you’ll have the choice of managing server nodes individually or collectively via a browser-based interface. • PowerEdge FC830: 4-socket scale-up server with unprecedented density and expandability OpenManage Essentials provides enterprise-level monitoring and control -

Javafx Compiler Maven Plugin
JavaFX Compiler Maven Plugin New version found at JavaFX Maven Plugin What does it do? The unique goal of this plugin is "compile". The plugin will compile javafx source files without interfering with the java compiler. It activates the javafxc Ant task using the Maven model to fill the classpath and other parameters. All generated class files will be generated under the standard maven dir "target /classes" and so packaged and distributed by Maven automatically. Resources Binaries distribution On JFrog public Artifactory repository jfrog-javafx-plugin The source code on JFrog subversion repository: jfrog-javafx-plugin The JIRA project for bug reports and next features: JFXCP The maven generated site: jfrog-javafx-plugin Activating the plugin Just add the following plugin to your pom.xml file: <plugin> <groupId>org.jfrog.maven.plugins</groupId> <artifactId>jfrog-javafx-plugin</artifactId> <executions> <execution> <goals> <goal>compile</goal> </goals> </execution> </executions> </plugin> And the following plugin repository to your settings.xml or pom.xml (best practice is to do it in a profile): <pluginRepository> <id>jfrog-plugins-dist</id> <name>jfrog-plugins-dist</name> <url>http://repo.jfrog.org/artifactory/plugins-releases-local</url> <snapshots> <enabled>false</enabled> </snapshots> </pluginRepository> JavaFX dependencies has Maven2 POM declaration To use javafx SDK jars in your project you need to declare the following dependencies in your POM file: <dependencies> <dependency> <groupId>javafx</groupId> <artifactId>javafxrt</artifactId> <version>1.1.1</version> </dependency> <dependency> <groupId>javafx</groupId> <artifactId>javafxgui</artifactId> <version>1.1.1</version> </dependency> </dependencies> Standard configuration The default source path for javafx project is: src/main/javafx and if you have resources under it you need to add in your POM: <resource> <directory>${project.basedir}/src/main/javafx</directory> <excludes> <exclude>**/*.fx</exclude> </excludes> </resource>. -

Vi Processor™ Card
Vi Processor™ Card General The Vi Processor™ Card fitted to the Soundcraft Vi Series™ contains 8 powerful LEXICON® Effects Processing Units and 35 high-quality BSS® 30-band Graphic Equalisers. LEXICON® Effects Each Effects Unit can be inserted into any Output/Main Master bus or into any Input Channel, or it can be patched as an FX Return to an Input Channel, fed from an Aux send. Each FX Unit supports up to 30 different professional LEXICON® Effects. Effect Parameters can be easily changed via the VST Screens at a location on the Surface corresponding to where the FX is inserted or patched. Additionally, the Parameters can be viewed and changed in the FX Overview Page in the main menu. All Parameters from the 8 Effects Units and for all Effects Type are stored in the desk Snapshots. BSS® Graphic Equalisers The 35 BSS® 30-band Graphic Equalizers are permanently assigned to the 32 Output Busses and the three Main Masters. All Parameters from the GEQs are stored in the desk Snapshots. LEXICON® Effects Format Depending on the selected Effect Type, the FX processor works internally in one of three formats: The FX processor always has Stereo Inputs and Outputs. If the FX Type needs only a Mono Input, the Left and Right Input Signal are summed together. If the FX Type outputs only a Mono Signal then the Output Signal is distributed to both the Left and Right Outputs. The MIX Parameter adjusts the ratio between the original (dry) signal and the effects (wet) signal. Figure 21-1: FX Processor Configurations. -

AMD FX Cpus Now Faster Than Ever—Unlocked Performance with Maximum Cores
How to Sell the New AMD FX CPUs Now Faster than Ever—Unlocked Performance with Maximum Cores Who’s it for? Gamers and Enthusiasts who want the most out of their PC. Sell it in 5 seconds. More Cores. More Speed. Unlocked1 More Cores > Up to 8 Cores > Only 8 Core Desktop Processor—2 cores more than Intel1 Maximum Speed > Up to 4.2GHz Turbo Clock Speed > Latest Technology and Worlds Highest Frequencies2 Unlocked & Overclockable > Get the Maximum Tunable Performance > Go up to 5.0 GHz with aggressive cooling solutions from AMD3 Sell it in 60 seconds. Unlocked Performance for Less Money1,4 Performance Ferocious power right out of the box. > The groundbreaking AMD FX 8-Core Processor Black Edition comes unlocked. No premium to pay. No code to input.Just unrestrained, overclocked power right away.4 > Groundbreaking technology. Epic performance. > This next-generation architecture takes 8-core processing to a new level. Test the limits to play harder and get more done. Speed The need for speed. AMD FX Processors—Unlocked and overclocked.4 > Incredible speed out of the box and more in the tank; AMD Turbo CORE Technology automatically kicks in, boosting performance to a user’s varied workload. > The sky’s the limit with this processor’s massive headroom. Go up to 5.0 GHz with aggressive cooling solutions from AMD.5 Price Price and performance that keeps getting better and more bang for your buck. Unlocked technology.4 Unbelievable pricing. > With more speed than ever and more aggressive price points – New AMD FX Processors raise the bar for 8-core computing. -

Activty 2.1.4 Force Vectors
Force Vectors Principles of Engineering © 2012 Project Lead The Way, Inc. Vectors Vector Quantities Have both a magnitude and direction Examples: Position, force, moment Vector Notation Vectors are given a variable, such as A or B Handwritten notation usually includes an arrow, such as A or B Illustrating Vectors Vectors are represented by arrows Include magnitude, direction, and sense Magnitude: The length of the line segment Magnitude = 3 30° +X Illustrating Vectors Vectors are represented by arrows Include magnitude, direction, and sense Direction: The angle between a reference axis and the arrow’s line of action Direction = 30° counterclockwise from the positive x-axis 30° +x Illustrating Vectors Vectors are represented by arrows Include magnitude, direction, and sense Sense: Indicated by the direction of the tip of the arrow Sense = Upward and to the right 30° +x Sense +y (up) +y (up) -x (left) +x (right) (0,0) -y (down) -y (down) -x (left) +x (right) Trigonometry Review Right Triangle A triangle with a 90° angle Sum of all interior angles = 180° Pythagorean Theorem: c2 = a2 + b2 Opposite Side (opp) 90° Adjacent Side (adj) Trigonometry Review Trigonometric Functions soh cah toa sin θ° = opp / hyp cos θ° = adj / hyp tan θ° = opp / adj Opposite Side (opp) 90° Adjacent Side (adj) Trigonometry Application The hypotenuse is the Magnitude of the Force, F In the figure here, The adjacent side is the x-component, Fx The opposite side is the y-component, Fy Opposite Side Fy 90° Adjacent Side Fx Trigonometry Application sin θ° = Fy / F Fy= F sin θ° cos θ° = Fx / F Fx= F cos θ° tan θ° = Fy / Fx Opposite Side Fy 90° Adjacent Side Fx Fx and Fy are negative if left or down, respectively. -

FX Benchmark Solutions Contents 02 Key Facts 03 IOSCO & Central Bank Activity 03 Data Hierarchy 04 Delivery Mechanism 04 Calculation 04 FAQ
A Bloomberg Professional Services Offering Bloomberg Terminal Foreign ExchangeForeign BFIX <GO> FX benchmark solutions Contents 02 Key facts 03 IOSCO & Central Bank activity 03 Data hierarchy 04 Delivery mechanism 04 Calculation 04 FAQ 2 BFIX <GO> overview Bloomberg’s BFIX family of benchmarks covers a wide array of FX instruments with a comprehensive coverage of global currencies. The benchmark is used by market participants who need to use foreign exchange rates for portfolio benchmarking, derivatives valuation, index construction, and trade execution. Key facts • BFIX is administered and calculated by Bloomberg with transparent methodology publicly available and easily replicable. • BFIX produces over 1,150 spot currency pairs, and 3,850 forward and NDF fixings. • 5,000 fixings are generated every 30 mins throughout the day where markets are open. • Results are published on the terminal to a dedicated screen BFIX <GO> within 15 seconds of the end of the fix for USD based Spots & Forwards and within 1 minute for all. Selected rates published on the website with a 5 min delay. 2 BFIX <GO> FX benchmark solutions IOSCO & Central Bank activity IOSCO (International Organization of Securities Commissions): The BGNE uses purely executable data from Bloomberg's FXGO platform delivering greater transparency into current Bloomberg announced May 11, 2016 the successful completion market liquidity. They are received from a diverse universe of of an independent assessment confirming the alignment of the sources who provide them for the primary purpose of soliciting BFIX family of benchmarks with the International Organization actual FX transactions from the market. of Securities Commissions (IOSCO) Principles. As of May 13 2018 the spot currency pairs in the table The assessment was conducted by Ernst & Young LLP (EY).