Derivation of Solar Position Formulae
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Planet Positions: 1 Planet Positions
Planet Positions: 1 Planet Positions As the planets orbit the Sun, they move around the celestial sphere, staying close to the plane of the ecliptic. As seen from the Earth, the angle between the Sun and a planet -- called the elongation -- constantly changes. We can identify a few special configurations of the planets -- those positions where the elongation is particularly noteworthy. The inferior planets -- those which orbit closer INFERIOR PLANETS to the Sun than Earth does -- have configurations as shown: SC At both superior conjunction (SC) and inferior conjunction (IC), the planet is in line with the Earth and Sun and has an elongation of 0°. At greatest elongation, the planet reaches its IC maximum separation from the Sun, a value GEE GWE dependent on the size of the planet's orbit. At greatest eastern elongation (GEE), the planet lies east of the Sun and trails it across the sky, while at greatest western elongation (GWE), the planet lies west of the Sun, leading it across the sky. Best viewing for inferior planets is generally at greatest elongation, when the planet is as far from SUPERIOR PLANETS the Sun as it can get and thus in the darkest sky possible. C The superior planets -- those orbiting outside of Earth's orbit -- have configurations as shown: A planet at conjunction (C) is lined up with the Sun and has an elongation of 0°, while a planet at opposition (O) lies in the opposite direction from the Sun, at an elongation of 180°. EQ WQ Planets at quadrature have elongations of 90°. -

Captain Vancouver, Longitude Errors, 1792
Context: Captain Vancouver, longitude errors, 1792 Citation: Doe N.A., Captain Vancouver’s longitudes, 1792, Journal of Navigation, 48(3), pp.374-5, September 1995. Copyright restrictions: Please refer to Journal of Navigation for reproduction permission. Errors and omissions: None. Later references: None. Date posted: September 28, 2008. Author: Nick Doe, 1787 El Verano Drive, Gabriola, BC, Canada V0R 1X6 Phone: 250-247-7858, FAX: 250-247-7859 E-mail: [email protected] Captain Vancouver's Longitudes – 1792 Nicholas A. Doe (White Rock, B.C., Canada) 1. Introduction. Captain George Vancouver's survey of the North Pacific coast of America has been characterized as being among the most distinguished work of its kind ever done. For three summers, he and his men worked from dawn to dusk, exploring the many inlets of the coastal mountains, any one of which, according to the theoretical geographers of the time, might have provided a long-sought-for passage to the Atlantic Ocean. Vancouver returned to England in poor health,1 but with the help of his brother John, he managed to complete his charts and most of the book describing his voyage before he died in 1798.2 He was not popular with the British Establishment, and after his death, all of his notes and personal papers were lost, as were the logs and journals of several of his officers. Vancouver's voyage came at an interesting time of transition in the technology for determining longitude at sea.3 Even though he had died sixteen years earlier, John Harrison's long struggle to convince the Board of Longitude that marine chronometers were the answer was not quite over. -

Sun Tool Options
Sun Study Tools Sophomore Architecture Studio: Lighting Lecture 1: • Introduction to Daylight (part 1) • Survey of the Color Spectrum • Making Light • Controlling Light Lecture 2: • Daylight (part 2) • Design Tools to study Solar Design • Architectural Applications Lecture 3: • Light in Architecture • Lighting Design Strategies Sun Tool Options 1. Paper and Pencil 2. Build a Model 3. Use a Computer The first step to any of these options is to define…. Where is the site? 1 2 Sun Study Tools North Latitude and Longitude South Longitude Latitude Longitude Sun Study Tools North America Latitude 3 United States e ud tit La Sun Study Tools New York 72w 44n 42n Site Location The site location is specified by a latitude l and a longitude L. Latitudes and longitudes may be found in any standard atlas or almanac. Chart shows the latitudes and longitudes of some North American cities. Conventions used in expressing latitudes are: Positive = northern hemisphere Negative = southern hemisphere Conventions used in expressing longitudes are: Positive = west of prime meridian (Greenwich, United Kingdom) Latitude and Longitude of Some North American Cities Negative = east of prime meridian 4 Sun Study Tools Solar Path Suns Position The position of the sun is specified by the solar altitude and solar azimuth and is a function of site latitude, solar time, and solar declination. 5 Sun Study Tools Suns Position The rotation of the earth about its axis, as well as its revolution about the sun, produces an apparent motion of the sun with respect to any point on the altitude earth's surface. The position of the sun with respect to such a point is expressed in terms of two angles: azimuth The sun's position in terms of solar altitude (a ) and azimuth (a ) solar azimuth, which is the t s with respect to the cardinal points of the compass. -

Equatorial and Cartesian Coordinates • Consider the Unit Sphere (“Unit”: I.E
Coordinate Transforms Equatorial and Cartesian Coordinates • Consider the unit sphere (“unit”: i.e. declination the distance from the center of the (δ) sphere to its surface is r = 1) • Then the equatorial coordinates Equator can be transformed into Cartesian coordinates: right ascension (α) – x = cos(α) cos(δ) – y = sin(α) cos(δ) z x – z = sin(δ) y • It can be much easier to use Cartesian coordinates for some manipulations of geometry in the sky Equatorial and Cartesian Coordinates • Consider the unit sphere (“unit”: i.e. the distance y x = Rcosα from the center of the y = Rsinα α R sphere to its surface is r = 1) x Right • Then the equatorial Ascension (α) coordinates can be transformed into Cartesian coordinates: declination (δ) – x = cos(α)cos(δ) z r = 1 – y = sin(α)cos(δ) δ R = rcosδ R – z = sin(δ) z = rsinδ Precession • Because the Earth is not a perfect sphere, it wobbles as it spins around its axis • This effect is known as precession • The equatorial coordinate system relies on the idea that the Earth rotates such that only Right Ascension, and not declination, is a time-dependent coordinate The effects of Precession • Currently, the star Polaris is the North Star (it lies roughly above the Earth’s North Pole at δ = 90oN) • But, over the course of about 26,000 years a variety of different points in the sky will truly be at δ = 90oN • The declination coordinate is time-dependent albeit on very long timescales • A precise astronomical coordinate system must account for this effect Equatorial coordinates and equinoxes • To account -

Solar Engineering Basics
Solar Energy Fundamentals Course No: M04-018 Credit: 4 PDH Harlan H. Bengtson, PhD, P.E. Continuing Education and Development, Inc. 22 Stonewall Court Woodcliff Lake, NJ 07677 P: (877) 322-5800 [email protected] Solar Energy Fundamentals Harlan H. Bengtson, PhD, P.E. COURSE CONTENT 1. Introduction Solar energy travels from the sun to the earth in the form of electromagnetic radiation. In this course properties of electromagnetic radiation will be discussed and basic calculations for electromagnetic radiation will be described. Several solar position parameters will be discussed along with means of calculating values for them. The major methods by which solar radiation is converted into other useable forms of energy will be discussed briefly. Extraterrestrial solar radiation (that striking the earth’s outer atmosphere) will be discussed and means of estimating its value at a given location and time will be presented. Finally there will be a presentation of how to obtain values for the average monthly rate of solar radiation striking the surface of a typical solar collector, at a specified location in the United States for a given month. Numerous examples are included to illustrate the calculations and data retrieval methods presented. Image Credit: NOAA, Earth System Research Laboratory 1 • Be able to calculate wavelength if given frequency for specified electromagnetic radiation. • Be able to calculate frequency if given wavelength for specified electromagnetic radiation. • Know the meaning of absorbance, reflectance and transmittance as applied to a surface receiving electromagnetic radiation and be able to make calculations with those parameters. • Be able to obtain or calculate values for solar declination, solar hour angle, solar altitude angle, sunrise angle, and sunset angle. -

Sarah Provancher Jeanne Hilt (502) 439-7138 (502) 614-4122 [email protected] [email protected]
FOR IMMEDIATE RELEASE: Tuesday, June 5, 2018 CONTACT: Sarah Provancher Jeanne Hilt (502) 439-7138 (502) 614-4122 [email protected] [email protected] DOWNTOWN TO SHOWCASE FÊTE DE LA MUSIQUE LOUISVILLE ON JUNE 21 ST Downtown Louisville to celebrate the Summer Solstice with live music and more than 30 street performers for a day-long celebration of French culture Louisville, KY – A little taste of France is coming to Downtown Louisville on the summer solstice, Thursday, June 21st, with Fête de la Musique Louisville (pronounced fet de la myzic). The event, which means “celebration of music” in French, has been taking place in Paris on the summer solstice since 1982. Downtown Louisville’s “celebration of music” is presented by Alliance Francaise de Louisville in conjunction with the Louisville Downtown Partnership (LDP). Music will literally fill the downtown streets all day on the 21st with dozens of free live performances over the lunchtime hour and during a special Happy Hour showcase on the front steps of the Kentucky Center from 5:30-7:30pm. A list of performance venues with scheduled performers from 11am-1pm are: Fourth Street Live! – Classical musicians including The NouLou Chamber Players, 90.5 WUOL Young Musicians and Harin Oh, GFA Youth Guitar Summit Kindred Plaza – Hewn From The Mountain, a local Irish band 400 W. Market Plaza – FrenchAxe, a French band from Cincinnati Old Forester Distillery – A local jug band The salsa band Milenio is the scheduled performance group for the Happy Hour also at Fourth Street Live! from 5 – 7 pm. "In Paris and throughout France, the Fête de la Musique is literally 24 hours filled with music by all types of musicians of all skill levels. -
Regents and Midterm Prep Answers
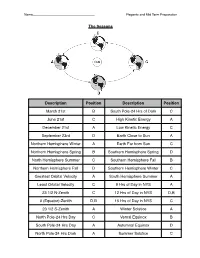
Name__________________________________!Regents and Mid Term Preparation The Seasons Description Position Description Position March 21st B South Pole-24 Hrs of Dark C June 21st C High Kinetic Energy A December 21st A Low Kinetic Energy C September 23rd D Earth Close to Sun A Northern Hemisphere Winter A Earth Far from Sun C Northern Hemisphere Spring B Southern Hemisphere Spring D North Hemisphere Summer C Southern Hemisphere Fall B Northern Hemisphere Fall D Southern Hemisphere Winter C Greatest Orbital Velocity A South Hemisphere Summer A Least Orbital Velocity C 9 Hrs of Day in NYS A 23 1/2 N-Zenith C 12 Hrs of Day in NYS D,B 0 (Equator)-Zenith D,B 15 Hrs of Day in NYS C 23 1/2 S-Zenith A Winter Solstice A North Pole-24 Hrs Day C Vernal Equinox B South Pole-24 Hrs Day A Autumnal Equinox D North Pole-24 Hrs Dark A Summer Solstice C Name__________________________________!Regents and Mid Term Preparation Sunʼs Path in NYS 1. What direction does the sun rise in summer? _____NE___________________ 2. What direction does the sun rise in winter? _________SE_________________ 3. What direction does the sun rise in fall/spring? ________E_______________ 4. How long is the sun out in fall/spring? ____12________ 5. How long is the sun out in winter? _________9______ 6. How long is the sun out in summer? ________15_______ 7. What direction do you look to see the noon time sun? _____S________ 8. What direction do you look to see polaris? _______N_________ 9. From sunrise to noon, what happens to the length of a shadow? ___SMALLER___ 10. -

Summer Solstice
A FREE RESOURCE PACK FROM EDMENTUM Summer Solstice PreK–6th Topical Teaching Grade Range Resources Free school resources by Edmentum. This may be reproduced for class use. Summer Solstice Topical Teaching Resources What Does This Pack Include? This pack has been created by teachers, for teachers. In it you’ll find high quality teaching resources to help your students understand the background of Summer Solstice and why the days feel longer in the summer. To go directly to the content, simply click on the title in the index below: FACT SHEETS: Pre-K – Grade 3 Grades 3-6 Grades 3-6 Discover why the Sun rises earlier in the day Understand how Earth moves and how it Discover how other countries celebrate and sets later every night. revolves around the Sun. Summer Solstice. CRITICAL THINKING QUESTIONS: Pre-K – Grade 2 Grades 3-6 Discuss what shadows are and how you can create them. Discuss how Earth’s tilt cause the seasons to change. ACTIVITY SHEETS AND ANSWERS: Pre-K – Grade 3 Grades 3-6 Students are to work in pairs to explain what happens during Follow the directions to create a diagram that describes the Summer Solstice. Summer Solstice. POSTER: Pre-K – Grade 6 Enjoyed these resources? Learn more about how Edmentum can support your elementary students! Email us at www.edmentum.com or call us on 800.447.5286 Summer Solstice Fact Sheet • Have you ever noticed in the summer that the days feel longer? This is because there are more hours of daylight in the summer. • In the summer, the Sun rises earlier in the day and sets later every night. -

Equation of Time — Problem in Astronomy M
This paper was awarded in the II International Competition (1993/94) "First Step to Nobel Prize in Physics" and published in the competition proceedings (Acta Phys. Pol. A 88 Supplement, S-49 (1995)). The paper is reproduced here due to kind agreement of the Editorial Board of "Acta Physica Polonica A". EQUATION OF TIME | PROBLEM IN ASTRONOMY M. Muller¨ Gymnasium M¨unchenstein, Grellingerstrasse 5, 4142 M¨unchenstein, Switzerland Abstract The apparent solar motion is not uniform and the length of a solar day is not constant throughout a year. The difference between apparent solar time and mean (regular) solar time is called the equation of time. Two well-known features of our solar system lie at the basis of the periodic irregularities in the solar motion. The angular velocity of the earth relative to the sun varies periodically in the course of a year. The plane of the orbit of the earth is inclined with respect to the equatorial plane. Therefore, the angular velocity of the relative motion has to be projected from the ecliptic onto the equatorial plane before incorporating it into the measurement of time. The math- ematical expression of the projection factor for ecliptic angular velocities yields an oscillating function with two periods per year. The difference between the extreme values of the equation of time is about half an hour. The response of the equation of time to a variation of its key parameters is analyzed. In order to visualize factors contributing to the equation of time a model has been constructed which accounts for the elliptical orbit of the earth, the periodically changing angular velocity, and the inclined axis of the earth. -

3.- the Geographic Position of a Celestial Body
Chapter 3 Copyright © 1997-2004 Henning Umland All Rights Reserved Geographic Position and Time Geographic terms In celestial navigation, the earth is regarded as a sphere. Although this is an approximation, the geometry of the sphere is applied successfully, and the errors caused by the flattening of the earth are usually negligible (chapter 9). A circle on the surface of the earth whose plane passes through the center of the earth is called a great circle . Thus, a great circle has the greatest possible diameter of all circles on the surface of the earth. Any circle on the surface of the earth whose plane does not pass through the earth's center is called a small circle . The equator is the only great circle whose plane is perpendicular to the polar axis , the axis of rotation. Further, the equator is the only parallel of latitude being a great circle. Any other parallel of latitude is a small circle whose plane is parallel to the plane of the equator. A meridian is a great circle going through the geographic poles , the points where the polar axis intersects the earth's surface. The upper branch of a meridian is the half from pole to pole passing through a given point, e. g., the observer's position. The lower branch is the opposite half. The Greenwich meridian , the meridian passing through the center of the transit instrument at the Royal Greenwich Observatory , was adopted as the prime meridian at the International Meridian Conference in 1884. Its upper branch is the reference for measuring longitudes (0°...+180° east and 0°...–180° west), its lower branch (180°) is the basis for the International Dateline (Fig. -

2 Coordinate Systems
2 Coordinate systems In order to find something one needs a system of coordinates. For determining the positions of the stars and planets where the distance to the object often is unknown it usually suffices to use two coordinates. On the other hand, since the Earth rotates around it’s own axis as well as around the Sun the positions of stars and planets is continually changing, and the measurment of when an object is in a certain place is as important as deciding where it is. Our first task is to decide on a coordinate system and the position of 1. The origin. E.g. one’s own location, the center of the Earth, the, the center of the Solar System, the Galaxy, etc. 2. The fundamental plan (x−y plane). This is often a plane of some physical significance such as the horizon, the equator, or the ecliptic. 3. Decide on the direction of the positive x-axis, also known as the “reference direction”. 4. And, finally, on a convention of signs of the y− and z− axes, i.e whether to use a left-handed or right-handed coordinate system. For example Eratosthenes of Cyrene (c. 276 BC c. 195 BC) was a Greek mathematician, elegiac poet, athlete, geographer, astronomer, and music theo- rist who invented a system of latitude and longitude. (According to Wikipedia he was also the first person to use the word geography and invented the disci- pline of geography as we understand it.). The origin of this coordinate system was the center of the Earth and the fundamental plane was the equator, which location Eratosthenes calculated relative to the parts of the Earth known to him. -

Celestial Coordinate Systems
Celestial Coordinate Systems Craig Lage Department of Physics, New York University, [email protected] January 6, 2014 1 Introduction This document reviews briefly some of the key ideas that you will need to understand in order to identify and locate objects in the sky. It is intended to serve as a reference document. 2 Angular Basics When we view objects in the sky, distance is difficult to determine, and generally we can only indicate their direction. For this reason, angles are critical in astronomy, and we use angular measures to locate objects and define the distance between objects. Angles are measured in a number of different ways in astronomy, and you need to become familiar with the different notations and comfortable converting between them. A basic angle is shown in Figure 1. θ Figure 1: A basic angle, θ. We review some angle basics. We normally use two primary measures of angles, degrees and radians. In astronomy, we also sometimes use time as a measure of angles, as we will discuss later. A radian is a dimensionless measure equal to the length of the circular arc enclosed by the angle divided by the radius of the circle. A full circle is thus equal to 2π radians. A degree is an arbitrary measure, where a full circle is defined to be equal to 360◦. When using degrees, we also have two different conventions, to divide one degree into decimal degrees, or alternatively to divide it into 60 minutes, each of which is divided into 60 seconds. These are also referred to as minutes of arc or seconds of arc so as not to confuse them with minutes of time and seconds of time.