DOCSLIB.ORG

Mechanisms of Visual Sensitivity: Backgrounds and Early Dark Adaptation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mechanisms of Visual Sensitivity: Backgrounds and Early Dark Adaptation i,%on Res. Vol. 23. No. I?. pp. 1423-3432.1983 0042-6989X3 53.00 + 0.00 Printed III Great Britain. Ail rights reserved Copyright .c 1983Pergamon Press Ltd MECHANISMS OF VISUAL SENSITIVITY: BACKGROUNDS AND EARLY DARK ADAPTATION WILSON S. GEISLER Department of Psychology, University of Texas, Austin, TX 78712. U.S.A. (Received 2 October 1980; in raised form 14 June 1983) Abstract-There is substantial physiological and psychophysical evidence for an adaptation mechanism whose effect, under many circumstances, is equivalent to placing a neutral density filter in front of the eye. Furthermore. this mechanism is of sufficient strength to predict the generalized Weber‘s law for increment thresholds on steady backgrounds. However, it was shown that an additional transient mechanism (with a time-course of around 100 msec) is also needed to account for the inc~ment-threshold results. The effect of this mechanism on increment thresholds during early dark adaptation was parametrically examined. Several models for the transient mechanism were considered. The one best able to account for the results consists of a subtractive inhibitory stage operating prior to a saturating nonlinearity. Light adaptation Dark adaptation Increment thresholds Lateral inhibition Weber’s law INTRODUCTION adaptation” model. The evidence comes from experi- In the cone system, increment and decrement thresh- ments in which flashed-background increment- olds measured against steady backgrounds are ap threshold functions were measured in the fovea under proximately described by Weber’s law over a wide various fixed states of light adaptation. For example. range of background intensities and test-field param- Geisler (1981) measured flashed-background eters. Substantial exceptions to the law occur for test increment-threshold functions 500 msec after the stimuli that are very small and brief (Barlow, 1958; offset of adapting backgrounds. Figure I shows the Geisfer, 1979a) or of high spatial or temporal fre- pattern of results obtained in the study. The solid quencies (Kelly, 1972); but. even under these condi- curve labelled - co is the increment-threshold func- tions the thresholds converge toward Weber’s law as tion obtained for flashed backgrounds in the dark- background intensity is raised. The widespread valid- adapted fovea. The other solid curves represent ity of Weber’s law across both stimulus conditions and species may be due to its usefulness for pattern recognition. In particular, Weber’s law implies that a visual system exhibit pattern constancy-the prop- erty that the set of visible lines and edges within the visual field remains constant across all illumination levels (Hemila, 1977; Geisler. 1978a). Many models for the adaptation processes under- lying Weber’s law have been proposed. These include logarithmic response compression coupled with a constant criterion for detection (Cornsweet and Pin- sker, 1965), power-law response compression with increasing internal variability (Mansfield, 19X), linear transduction with quanta1 fluctuations and sources of correlated neural noise (Triesman, 1966), power-law transduction followed by a multiplicative adaptation factor (Thijssen and Vendrik. 1971), and 0 I 2 3 4 5 nonlinear transduction preceded by a multiplicative LO6 BICKMOUNO adaptation factor (Lythgoe. 1936: Craik, 1938; Geis- Fig. I. The pattern of increment-threshold functions ler. 1975: 1981: Dawis and Purple. 1980). Recently, reported in Geisler (1981). The solid curves are psychophysical evidence has been accumulating for washy-background inc~ment-th~hold functions obtained the latter type of model (Geisler. 197Xb. 1981: Hood, at various fixed levels of adaptation. The dashed curve is the optimal function that can be obtained with multiplicative 1978; Hood ef ui.. 1978). which will be referred to adaptation. The dotted curve shows the actual function that here as the “dark-glasses” or “multiplicative- is obtained. 1423 1424 WILSON S. GEISLEK flashed-background increment-thr~shoId functions steady backgrounds that would be obtained if only obtained for the adapting-background intensities in- multiplicative adaptation were operating. The dotted dicated on the left. The functions obtained at all curve shows the function that is obtained: it is 0.7-l .O adapting-background intensities are roughly identical log units lower than the dashed curve at moderate to in shape and continuously accelerating when plotted high background levels. Changes in the maximum of in log-log coordinates. Furthermore, a function ob- the intensity-response function, as least of the sort tained at any given adapting-background intensity observed in electrophysiological research. are also can be brought into coincidence with a function unable to account for the results. Typically. light obtained at any other intensity by translation along adaptation decreases the maximum of the inten- a 45 line. This is exactly the prediction made by the sity-response function which should cause increment simple multiplicative-adaptation model (Geisler, thresholds to increase rather than decrease. 1978b). There appears to be at least one other factor or Figure 1 is also useful for explaining how multi- mechanism responsible for the increment thresholds plicative adaptation accounts for Weber’s iaw. The obtained with steady adapting backgrounds. Experi- X’s indicate the point on each curve where the ments in which the adapting background is momen- minimum Weber fraction (AZ/l) is reached. AS can be tarily switched off and on just before presentation of seen. the points where the Weber fraction reaches its the increment field (Ikeda and Boynton. 1965: Gei- minimum trace out a straight line of slope one (the sler, 1981) provide further evidence for this additional dashed line). In the standard increment-threshold mechanism. These studies indicate that this mech- experiment the adapting-background intensity and anism has a relatively quick decay time---on the order the background intensity against which threshold is of 100 msec. The purpose of the present experiments measured are identical. Now, if the adapting back- was to further explore this mechanism which is grounds produce just enough multiplicative adapta- apparently involved in the very early phases of light tion for the flashed-background increment-threshold and dark adaptation. curves to shift so that their minimum Weber fractions occur at the adapting-background intensity, then the increment-thresholds must be given by the X’s. In THEOR\ other words. Weber’s law is predicted. The results in Electrophysiological studies. including those listed Geisler ( 198 1) confirm that the increment-threshold in the introduction. have often found that the curves shift sufficiently to yield Weber’s law. flash-response characteristics of retinal neurons in the There is also considerable electrophysiological evi- vertebrate retina are described by the equation dence for the multiplicative adaptation model (Naka I” and Rushton, 1966; Dowling and Ripps, 1971, 1972; R = R,,, -. I” + I,” Glantz. 1972: Grabowski ef ai., 1972; Baylor and Hodgkin. 1974: Norman and Werblin, 1974; Werblin, where I is the intensity of the flash, R,,, is the 1974: Kleinschmidt and Dowling, 1975; Green ef al., maximum electrical response of the neuron. I, is the 1975: Fain, 1976; Norman and Perlman, 1979; Dawis half-saturation constant. and n is an exponent with a and Purple. 1980; Valeton and Norren, 1983). Most value usually between 0.7 and 1.0. As mentioned of these studies measured the effects of either bleaches above, changes in the flash-response characteristic or backgrounds on the intensity-response functions due to bleaching and backgrounds can usually be of retinal neurons. especially receptors. Typically it described by changes in I, (that is. by multiplicative was found that most of the changes in the intensity- adaptation) and by changes in R,,, (the maximum response functions are attributable to multiplicative response). In a previous paper (Geisler. 1981). a adaptation (i.e. to changes in the half-saturation simple model based on equation (I) was shown to constant). It is also typically found that light adapta- account fairly well for the effects of bleaches and tion produces some relatively small decreases in the backgrounds on flashed-background increment- maximum of the intensity-response function. Psycho- threshoId functions. It was assumed that threshold is physically. there is little evidence of such decreases reached when the response R , to the background- (Geisler. 1981); however. one would not expect the plus-increment exceeds the response R to the back- small effects observed in most electrophysiological ground alone by some fixed criterion amount (5. That studies to have much influence on the psychophysical is. threshold is reached when results. Although the multiplicative adaptation observed in R, - R=ii. (2) electrophysiological recordings, and in the appropri- The arguments in equation (1) for R + and R are, ate psychophysical experiments, is sufficient to respectively account for Weber’s law. the actual increment- threshold function obtained for steady backgrounds AI + s’ I i- ;: I, (3) cannot be explained by multiplicative adaptation alone (Geisler. 1981). The dashed curve in Fig. 1 and shows the (optimal) increment-threshold function for Mechanisms of visual sensitivity: backgrounds and early dark adaptation 1425 where I, is the intensity of the adapting background, intensity-r~ponse functions ~flash-response charac- and < and 1’are parameters
Load more

Recommended publications
  • Auditory Experience Controls the Maturation of Song Discrimination and Sexual Response in Drosophila Xiaodong Li, Hiroshi Ishimoto, Azusa Kamikouchi*
    RESEARCH ARTICLE Auditory experience controls the maturation of song discrimination and sexual response in Drosophila Xiaodong Li, Hiroshi Ishimoto, Azusa Kamikouchi* Graduate School of Science, Nagoya University, Nagoya, Japan Abstract In birds and higher mammals, auditory experience during development is critical to discriminate sound patterns in adulthood. However, the neural and molecular nature of this acquired ability remains elusive. In fruit flies, acoustic perception has been thought to be innate. Here we report, surprisingly, that auditory experience of a species-specific courtship song in developing Drosophila shapes adult song perception and resultant sexual behavior. Preferences in the song-response behaviors of both males and females were tuned by social acoustic exposure during development. We examined the molecular and cellular determinants of this social acoustic learning and found that GABA signaling acting on the GABAA receptor Rdl in the pC1 neurons, the integration node for courtship stimuli, regulated auditory tuning and sexual behavior. These findings demonstrate that maturation of auditory perception in flies is unexpectedly plastic and is acquired socially, providing a model to investigate how song learning regulates mating preference in insects. DOI: https://doi.org/10.7554/eLife.34348.001 Introduction Vocal learning in infants or juvenile birds relies heavily on the early experience of the adult conspe- cific sounds. In humans, early language input is necessary to form the ability of phonetic distinction *For correspondence: and pattern detection in the phase of auditory learning (Doupe and Kuhl, 1999; Kuhl, 2004). [email protected] Because of the strong parallels between speech acquisition of humans and song learning of song- Competing interests: The birds, and the difficulties to investigate the neural mechanisms of human early auditory memory at authors declare that no cellular resolution, songbirds have been used as a predominant model in studying memory formation competing interests exist.
    [Show full text]
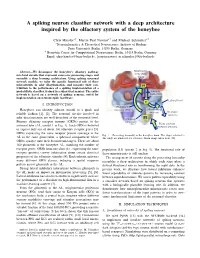
  • A Spiking Neuron Classifier Network with a Deep Architecture Inspired By
    A spiking neuron classifier network with a deep architecture inspired by the olfactory system of the honeybee Chris Hausler¨ ∗†, Martin Paul Nawrot∗† and Michael Schmuker∗† ∗Neuroinformatics & Theoretical Neuroscience, Institute of Biology Freie Universitat¨ Berlin, 14195 Berlin, Germany † Bernstein Center for Computational Neuroscience Berlin, 10115 Berlin, Germany Email: [email protected], fmartin.nawrot, [email protected] Abstract—We decompose the honeybee’s olfactory pathway Mushroom into local circuits that represent successive processing stages and body (MB) calyx resemble a deep learning architecture. Using spiking neuronal network models, we infer the specific functional role of these microcircuits in odor discrimination, and measure their con- 2 tribution to the performance of a spiking implementation of a probabilistic classifier, trained in a supervised manner. The entire Kenyon network is based on a network of spiking neurons, suited for Cells (KC) implementation on neuromorphic hardware. Lateral horn 3 I. INTRODUCTION Projection Honeybees can identify odorant stimuli in a quick and neurons (PN) MB-extrinsic neurons To motor reliable fashion [1], [2]. The neuronal circuits involved in neurons odor discrimination are well described at the structural level. 1 Antennal Primary olfactory receptor neurons (ORNs) project to the lobe (AL) From odorant antennal lobe (AL, circuit 1 in Fig. 1). Each ORN is believed receptor neurons to express only one of about 160 olfactory receptor genes [3]. ORNs expressing the same receptor protein converge in the Fig. 1. Processing hierarchy in the honeybee brain. The stages relevant to AL in the same glomerulus, a spherical compartment where this study are numbered for reference.
    [Show full text]
  • 1P MON. PM Cortex and Subcortical Auditory Nuclei
    dynamic role for the vestibular system in orientation and flight control. Laboratory studies of flight behavior under illuminated and dark conditions in both static and rotating obstacle tests were carried out while administering heavy water ͑D2O͒ to bats to impair their vestibular inputs. Eptesicus carried out complex maneuvers through both fixed arrays of wires and a rotating obstacle array using both vision and echolocation, or when guided by echolocation alone. When treated with D2O in combination with lack of visual cues, bats showed considerable decrements in performance. These data indicate that big brown bats use both vision and echolocation to provide spatial registration for head position information generated by the vestibular system. 2:55 1pAB3. Bat’s auditory system: Corticofugal feedback and plasticity. Nobuo Suga ͑Dept. of Biol., Washington Univ., One Brookings Dr., St. Louis, MO 63130͒ The auditory system of the mustached bat consists of physiologically distinct subdivisions for processing different types of biosonar information. It was found that the corticofugal ͑descending͒ auditory system plays an important role in improving and adjusting auditory signal processing. Repetitive acoustic stimulation, cortical electrical stimulation or auditory fear conditioning evokes plastic changes of the central auditory system. The changes are based upon egocentric selection evoked by focused positive feedback associated with lateral inhibition. Focal electric stimulation of the auditory cortex evokes short-term changes in the auditory 1p MON. PM cortex and subcortical auditory nuclei. An increase in a cortical acetylcholine level during the electric stimulation changes the cortical changes from short-term to long-term. There are two types of plastic changes ͑reorganizations͒: centripetal best frequency shifts for expanded reorganization of a neural frequency map and centrifugal best frequency shifts for compressed reorganization of the map.
    [Show full text]
  • Krogh's Principle
    Introduction to Neuroscience: Behavioral Neuroscience Neuroethology, Comparative Neuroscience, Natural Neuroscience Nachum Ulanovsky Department of Neurobiology, Weizmann Institute of Science 2017-2018, 2nd semester Principles of Neuroethology Neuroethology seeks to understand the mechanisms by which the Neurobiology central nervous system controls the Neuroethology Ethology natural behavior of animals. • Focus on Natural behaviors: Choosing to study a well-defined and reproducible yet natural behavior (either Innate or Learned behavior) • Need to study thoroughly the animal’s behavior, including in the field: Neuroethology starts with a good understanding of Ethology. • If you study the animals in the lab, you need to keep them in conditions as natural as possible, to avoid the occurrence of unnatural behaviors. • Krogh’s principle 1 Krogh’s principle August Krogh Nobel prize 1920 “For such a large number of problems there will be some animal of choice or a few such animals on which it can be most conveniently studied. Many years ago when my teacher, Christian Bohr, was interested in the respiratory mechanism of the lung and devised the method of studying the exchange through each lung separately, he found that a certain kind of tortoise possessed a trachea dividing into the main bronchi high up in the neck, and we used to say as a laboratory joke that this animal had been created expressly for the purposes of respiration physiology. I have no doubt that there is quite a number of animals which are similarly "created" for special physiological
    [Show full text]
  • Lateral Inhibition Effects Demonstrate That the Maturational State of Neurons That Then Inhibit Their Neighbors
    522 Lateral Inhibition effects demonstrate that the maturational state of neurons that then inhibit their neighbors. When a the learner’s brain is crucial for the attainment of stimulus (such as a bar of light or any other stim- a language system. ulus) excites a number of neurons in the network Several questions remain open about the mecha- (in this case neurons 4e, 5e, 6e, and 7e), the effect nisms underlying language learning. One issue is of inhibition is to suppress the neurons just out- whether specific aspects of language acquisition side the edge of the bar (3e and 8e) because those should be attributed to language-specific versus neurons are inhibited but not excited. Further, general-purpose learning mechanisms. Another issue because the neurons just inside the edges of the is whether children’s native language can affect the bar (4e and 7e) are excited by light and only inhib- way they think, and whether language is necessary ited by one neighbor, they are especially active. or helpful for the development of human concepts. This leads to perceptual contrast enhancement at borders. Further research showed that lateral inhi- Anna Papafragou bition also applied to overlapping stimuli, and that its strength fell off with distance between the See also Aphasias; Audition: Cognitive Influences; Context Effects in Perception; Speech Perception; Top- interacting stimuli. Down and Bottom-Up Processing; Word Recognition Haldan Keffer Hartline won the Nobel Prize in 1967 for discovering lateral inhibition and its neu- ral correlates. The first inhibitory circuit in the Further Readings nervous system was found in the horseshoe crab (Limulus polyphemus).
    [Show full text]
  • Sensory Receptors A17 (1)
    SENSORY RECEPTORS A17 (1) Sensory Receptors Last updated: April 20, 2019 Sensory receptors - transducers that convert various forms of energy in environment into action potentials in neurons. sensory receptors may be: a) neurons (distal tip of peripheral axon of sensory neuron) – e.g. in skin receptors. b) specialized cells (that release neurotransmitter and generate action potentials in neurons) – e.g. in complex sense organs (vision, hearing, equilibrium, taste). sensory receptor is often associated with nonneural cells that surround it, forming SENSE ORGAN. to stimulate receptor, stimulus must first pass through intervening tissues (stimulus accession). each receptor is adapted to respond to one particular form of energy at much lower threshold than other receptors respond to this form of energy. adequate (s. appropriate) stimulus - form of energy to which receptor is most sensitive; receptors also can respond to other energy forms, but at much higher thresholds (e.g. adequate stimulus for eye is light; eyeball rubbing will stimulate rods and cones to produce light sensation, but threshold is much higher than in skin pressure receptors). when information about stimulus reaches CNS, it produces: a) reflex response b) conscious sensation c) behavior alteration SENSORY MODALITIES Sensory Modality Receptor Sense Organ CONSCIOUS SENSATIONS Vision Rods & cones Eye Hearing Hair cells Ear (organ of Corti) Smell Olfactory neurons Olfactory mucous membrane Taste Taste receptor cells Taste bud Rotational acceleration Hair cells Ear (semicircular
    [Show full text]
  • The Retina the Retina the Pigment Layer Contains Melanin That Prevents Light Reflection Throughout the Globe of the Eye
    The Retina The retina The pigment layer contains melanin that prevents light reflection throughout the globe of the eye. It is also a store of Vitamin A. Rods and Cones Photoreceptors of the nervous system responsible for transforming light energy into the electrical energy of the nervous system. Bipolar cells Link between photoreceptors and ganglion cells. Horizontal cells Provide inhibition between bipolar cells. This is the mechanism of lateral inhibition which is important to edge detection and contrast enhancement. Amacrine cells Transmit excitatory signals from bipolar to ganglion cells. Thought to be important in signalling changes in light intensity. Neural circuitry About 125 rods and 5 cones converge on each optic nerve fibre. In the central portion of the fovea there are no rods. The ratio of cones to optic nerves in the fovea is one. This increases the visual acuity of the fovea. Rods and Cones Photosensitive substance in rods is called rhodopsin and in cones is called iodopsin. The Photochemistry of Vision Rhodopsin and Iodopsin Cis-retinal +Opsin Light sensitive Light Trans-retinal Opsin Light insensitive This is a reversible reaction Cis-retinal +Opsin Light sensitive Vitamin A In the presence of light, the rods and cones are hyperpolarized mv t Hyperpolarizing potential lasts for upto half a second, leading to the perception of fusion of flickering lights. Receptor potential – rod and cone potential Hyperpolarizing receptor potential caused by rhodopsin decomposition. Hyperpolarizing potential lasts for upto half a second, leading to the fusion of flickering lights. Light and dark adaptation in the visual system The eye is capable of vision in conditions of light that vary greatly in intensity The eye adapts dynamically to lighting conditions Light and Dark Adaptation We are able to see in light intensities that vary greatly.
    [Show full text]
  • Small and Dim Target Detection Via Lateral Inhibition Filtering and Artificial Bee Colony Based Selective Visual Attention
    Small and Dim Target Detection via Lateral Inhibition Filtering and Artificial Bee Colony Based Selective Visual Attention Haibin Duan1,2*, Yimin Deng1,2, Xiaohua Wang2, Chunfang Xu1 1 State Key Laboratory of Virtual Reality Technology and Systems, School of Automation Science and Electrical Engineering, Beihang University (formerly Beijing University of Aeronautics and Astronautics), Beijing, P. R. China, 2 Science and Technology on Aircraft Control Laboratory, Beihang University, Beijing, P. R. China Abstract This paper proposed a novel bionic selective visual attention mechanism to quickly select regions that contain salient objects to reduce calculations. Firstly, lateral inhibition filtering, inspired by the limulus’ ommateum, is applied to filter low- frequency noises. After the filtering operation, we use Artificial Bee Colony (ABC) algorithm based selective visual attention mechanism to obtain the interested object to carry through the following recognition operation. In order to eliminate the camera motion influence, this paper adopted ABC algorithm, a new optimization method inspired by swarm intelligence, to calculate the motion salience map to integrate with conventional visual attention. To prove the feasibility and effectiveness of our method, several experiments were conducted. First the filtering results of lateral inhibition filter were shown to illustrate its noise reducing effect, then we applied the ABC algorithm to obtain the motion features of the image sequence. The ABC algorithm is proved to be more robust and effective through the comparison between ABC algorithm and popular Particle Swarm Optimization (PSO) algorithm. Except for the above results, we also compared the classic visual attention mechanism and our ABC algorithm based visual attention mechanism, and the experimental results of which further verified the effectiveness of our method.
    [Show full text]
  • Neurons Could Be Explained by the Asymmetrical Arrangement Ofon
    J. Physiol. (1965), 178, pp. 477-504 477 With 11 text-ftgureas Printed in Great Britain THE MECHANISM OF DIRECTIONALLY SELECTIVE UNITS IN RABBIT'S RETINA BY H. B. BARLOW* AND W. R. LEVICKt From the Physiological Laboratory, University of Cambridge and the Neurosensory Laboratory, School of Optometry, University of California, Berkeley 4, U.S.A. (Received 29 September 1964) Directionally selective single units have recently been found in the cerebral cortex of cats (Hubel, 1959; Hubel & Wiesel, 1959, 1962), the optic tectum of frogs and pigeons (Lettvin, Maturana, McCulloch & Pitts, 1959; Maturana & Frenk, 1963), and the retinae of rabbits (Barlow & Hill, 1963; Barlow, Hill & Levick, 1964). The term 'directionally selective' means that a unit gives a vigorous discharge of impulses when a stimulus object is moved through its receptive field in one direction (called the preferred direction), whereas motion in the reverse direction (called null) evokes little or no response. The preferred direction differs in different units, and the activity of a set of such units signals the direction of move- ment of objects in the visual field. In the rabbit the preferred and null directions cannot be predicted from a map ofthe receptive field showing the regions yielding on or off-responses to stationary spots. Furthermore, the preferred direction is unchanged by changing the stimulus; in particular, reversing the contrast of a spot or a black-white border does not reverse the preferred direction. Hubel & Wiesel (1962) thought that the directional selectivity of the cat's cortical neurons could be explained by the asymmetrical arrangement of on and off zones in the receptive field, and the simple interaction of effects summated over these zones, but the foregoing results rule out this explanation, at least in the rabbit's retina (Barlow & Hill, 1963).
    [Show full text]
  • Three Levels of Lateral Inhibition: a Space–Time Study of the Retina of the Tiger Salamander
    The Journal of Neuroscience, March 1, 2000, 20(5):1941–1951 Three Levels of Lateral Inhibition: A Space–Time Study of the Retina of the Tiger Salamander Botond Roska, Erik Nemeth, Laszlo Orzo, and Frank S. Werblin Division of Neurobiology, Department of Molecular and Cell Biology, University of California at Berkeley, Berkeley, California 94720 The space–time patterns of activity generated across arrays of feedback to bipolar terminals compresses the spatial represen- retinal neurons can provide a sensitive measurement of the tation of the stimulus bar at ON bipolar terminals over time. effects of neural interactions underlying retinal activity. We mea- Third, we showed that a third spatiotemporal compression sured the excitatory and inhibitory components associated with exists at the ganglion cell layer that is mediated by feedforward these patterns at each cellular level in the retina and further amacrine cells via GABAA receptors. These three inhibitory dissected inhibitory components pharmacologically. Using per- mechanisms, via three different receptor types, appear to com- forated and loose patch recording, we measured the voltages, pensate for the effects of lateral diffusion of activity attributable currents, or spiking at 91 lateral positions covering ϳ2mmin to dendritic spread and electrical coupling between retinal neu- response to a flashed 300-␮m-wide bar. First, we showed how rons. As a consequence, the width of the final representation at the effect of well known lateral inhibition at the outer retina, the ganglion cell level approximates the dimensions of the mediated by horizontal cells, evolved in time to compress the original stimulus bar. spatial representation of the stimulus bar at ON and OFF bipolar cell bodies as well as horizontal cells.
    [Show full text]
  • Somatosensory Evoked Potentials Indexing Lateral Inhibition
    bioRxiv preprint doi: https://doi.org/10.1101/2020.10.15.338111; this version posted October 16, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Somatosensory evoked potentials indexing lateral inhibition are modulated according to the mode of perceptual processing: comparing or combining multi-digit tactile motion Irena Arslanova**1, Keying Wang1, Hiroaki Gomi2, Patrick Haggard1 ** Corresponding author Affiliations: 1) Institute of Cognitive Neuroscience, University College London, 17 Queen Square London, WC1N 3AZ, UK 2) NTT Communication Science Laboratories, NTT Corporation, 3-1 Wakamiya, Morinosato, Atsugishi, Kanagawa, 243-0198, Japan Corresponding author contact details: Irena Arslanova: [email protected] +44(0)2076791177 ORCID: https://orcid.org/0000-0002-2981-3764 Institute of Cognitive Neuroscience, University College London, 17 Queen Square London, WC1N 3AZ, UK Supplemental information: Supplemental information includes a spreadsheet with data used for key inferences: ERP P40 amplitudes and behavioural accuracy, as well as percentage of rejected trials. It also includes an analysis of SEPs without the low-pass filter. Acknowledgements: This study was supported by a research contract between NTT and UCL, and an MRC-CASE studentship MR/P015778/1. Declaration of interests: The authors declare no competing financial interests. Data and code availability: Spreadsheet with mean P40 amplitudes, behavioural data, and percentage of rejected trials is deposited in Supplemental Information. EEG data along with a pre- processing and analysis script are available here: https://osf.io/f3u7r/?view_only=ca34821908b54047a36a459f8ed9b7ac.
    [Show full text]
  • Modeling Lateral Inhibition
    Modeling Lateral Inhibition Master’s Thesis Aalborg University Biomedical Engineering & Informatics Spring 2018 Group 10405 Barak El-Omar Navinder Singh Dhillon School of Medicine and Health Fredrik Bajers Vej 7 DK-9220 Aalborg Ø http://smh.aau.dk Title: Abstract: Modeling Lateral Inhibition Lateral inhibition is characterized by Theme: sharpening of a sensory sensation and plays Master’s thesis a crucial role in discrimination of sensory input. [Strominger et al., 2012] One as- Project Period: pect of lateral inhibition is that localization Spring Semester 2018 of stimuli has shown to be more difficult for noxious stimuli compared to innocu- Project Group: ous stimuli [Quevedo et al., 2017; Frahm Group 10405 et al., 2017]. In order to investigate the discriminatory differences between noxious Participant(s): and innocuous stimuli a single-layer arti- Barak El-Omar ficial neural network was developed and Navinder Singh Dhillon trained in MATLAB R2017b (MathWorks inc.) modelling lateral inhibition for both Supervisor(s): noxious and innocuous stimuli. The model Main-supervisor: Steffen Frahm was trained using the Gradient descent CO-supervisor: Carsten Dahl Mørch method with two-point discrimination data Page Numbers: 79 acquired from Frahm et al.[2017]. A val- idation of the lateral inhibition model for Date of Completion: laser stimulation showed that it was able 07/06-2018 to fit the training data with a prediction error of 0.0102 mm. However, the model was not able to generalize solutions com- pared to the lateral inhibition model for mechanical stimulation. The reason being the lateral inhibition model for mechanical stimulation had a prediction error of 0.0618 mm and therefore not fitted to the training data to the same extent as for laser stimu- lation.
    [Show full text]