Relevance of Newtonian Seismic Noise for the VIRGO Interferometer Sensitivity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Atomic Gas Far Away from the Virgo Cluster Core Galaxy NGC 4388
Astronomy & Astrophysics manuscript no. H4396 November 5, 2018 (DOI: will be inserted by hand later) Atomic gas far away from the Virgo cluster core galaxy NGC 4388 A possible link to isolated star formation in the Virgo cluster? B. Vollmer, W. Huchtmeier Max-Planck-Institut f¨ur Radioastronomie, Auf dem H¨ugel 69, D-53121 Bonn, Germany Received / Accepted 7 ′ Abstract. We have discovered 6 10 M⊙ of atomic gas at a projected distance greater than 4 (20 kpc) from the highly inclined Virgo spiral galaxy NGC 4388. This gas is most probably connected to the very extended Hα plume detected by Yoshida et al. (2002). Its mass makes a nuclear outflow and its radial velocity a minor merger as the origin of the atomic and ionized gas very unlikely. A numerical ram pressure simulation can account for the observed Hi spectrum and the morphology of the Hα plume. An additional outflow mechanism is still needed to reproduce the velocity field of the inner Hα plume. The extraplanar compact Hii region recently found by Gerhard et al. (2002) can be explained as a stripped gas cloud that collapsed and decoupled from the ram pressure wind due to its increased surface density. The star-forming cloud is now falling back onto the galaxy. Key words. Galaxies: individual: NGC 4388 – Galaxies: interactions – Galaxies: ISM – Galaxies: kinematics and dynamics 1. Introduction stripping. Based on their data they favoured a combina- tion of (iii) and (iv). Yoshida et al. (2002) on the other The Virgo cluster spiral galaxy NGC 4388 is located at hand favoured scenario (i) and (iv). -

Messier Objects
Messier Objects From the Stocker Astroscience Center at Florida International University Miami Florida The Messier Project Main contributors: • Daniel Puentes • Steven Revesz • Bobby Martinez Charles Messier • Gabriel Salazar • Riya Gandhi • Dr. James Webb – Director, Stocker Astroscience center • All images reduced and combined using MIRA image processing software. (Mirametrics) What are Messier Objects? • Messier objects are a list of astronomical sources compiled by Charles Messier, an 18th and early 19th century astronomer. He created a list of distracting objects to avoid while comet hunting. This list now contains over 110 objects, many of which are the most famous astronomical bodies known. The list contains planetary nebula, star clusters, and other galaxies. - Bobby Martinez The Telescope The telescope used to take these images is an Astronomical Consultants and Equipment (ACE) 24- inch (0.61-meter) Ritchey-Chretien reflecting telescope. It has a focal ratio of F6.2 and is supported on a structure independent of the building that houses it. It is equipped with a Finger Lakes 1kx1k CCD camera cooled to -30o C at the Cassegrain focus. It is equipped with dual filter wheels, the first containing UBVRI scientific filters and the second RGBL color filters. Messier 1 Found 6,500 light years away in the constellation of Taurus, the Crab Nebula (known as M1) is a supernova remnant. The original supernova that formed the crab nebula was observed by Chinese, Japanese and Arab astronomers in 1054 AD as an incredibly bright “Guest star” which was visible for over twenty-two months. The supernova that produced the Crab Nebula is thought to have been an evolved star roughly ten times more massive than the Sun. -

Downloading Rectification Matrices the first Step Will Be Downloading the Correct Rectification Matrix for Your Data Off of the OSIRIS Website
UNDERGRADUATE HONORS THESIS ADAPTIVE-OPTICS INTEGRAL-FIELD SPECTROSCOPY OF NGC 4388 Defended October 28, 2016 Skylar Shaver Thesis Advisor: Dr. Julie Comerford, Astronomy Honor Council Representative: Dr. Erica Ellingson, Astronomy Committee Members: Dr. Francisco Müller-Sánchez, Astrophysics Petger Schaberg, Writing Abstract Nature’s most powerful objects are well-fed supermassive black holes at the centers of galaxies known as active galactic nuclei (AGN). Weighing up to billions of times the mass of our sun, they are the most luminous sources in the Universe. The discovery of a number of black hole-galaxy relations has shown that the growth of supermassive black holes is closely related to the evolution of galaxies. This evidence has opened a new debate in which the fundamental questions concern the interactions between the central black hole and the interstellar medium within the host galaxy and can be addressed by studying two crucial processes: feeding and feedback. Due to the nature of AGN, high spatial resolution observations are needed to study their properties in detail. We have acquired near infrared Keck/OSIRIS adaptive optics-assisted integral field spectroscopy data on 40 nearby AGN as part of a large program aimed at studying the relevant physical processes associated with AGN phenomenon. This program is called the Keck/OSIRIS nearby AGN survey (KONA). We present here the analysis of the spatial distribution and two-dimensional kinematics of the molecular and ionized gas in NGC 4388. This nearly edge-on galaxy harbors an active nucleus and exhibits signs of the feeding and feedback processes. NGC 4388 is located in the heart of the Virgo cluster and thus is subject to possible interactions with the intra-cluster medium and other galaxies. -

Spring Constellations Leo
Night Sky 101: Spring Constellations Leo Leo, the lion, is very recognizable by the head of the lion, which looks like a backwards question mark, and is commonly known as “the sickle.” Regulus, Leo’s brightest star, is also easy to pick out in most lights. The constellation is best seen in April and May, but rises after the Spring Equinox in March. Within the constellation, there are several spiral galaxies: M65, M66, M95, and M96. It is possible to fit M65 and M66 into the same view on a low powered telescope. In Greek mythology, Leo was the Nemean lion, who was completely impervious to bronze, steel and any kind of metal. As part of his 12 labors, Hercules was charged to fight the lion and killed him Photo Credit: Starry Night by strangling him. Hercules took the lion’s pelt as a prize and Leo, the lion, was placed in the stars to commemorate their fight. Virgo Virgo is best seen in the late spring and early summer, usually May to June. The bright star Arcturus, in the constellation Boötes, lines up with the Virgo’s brightest star Spica, which makes it easy to find. Within the constellation is the Virgo Galaxy Cluster, which is a conglomerate of thousands of unnamed galaxies. These galaxies are about 65 million light years away, and usually only appear as smudges in a telescope. Virgo, the maiden, is also known as Persephone, or the daughter of the Demeter. Hades, god of the Un- derworld, fell in love with Virgo and took her to the Underworld. -
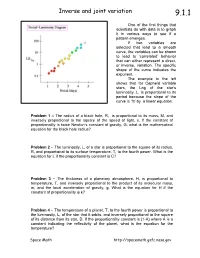
Inverse and Joint Variation 9.1.1
Inverse and joint variation 9.1.1 One of the first things that scientists do with data is to graph it in various ways to see if a pattern emerges. If two variables are selected that lead to a smooth curve, the variables can be shown to lead to ‘correlated’ behavior that can either represent a direct, or inverse, variation. The specific shape of the curve indicates the exponent. The example to the left shows that for Cepheid variable stars, the Log of the star’s luminosity, L, is proportional to its period because the slope of the curve is ‘fit’ by a linear equation. Problem 1 – The radius of a black hole, R, is proportional to its mass, M, and inversely proportional to the square of the speed of light, c. If the constant of proportionality is twice Newton’s constant of gravity, G, what is the mathematical equation for the black hole radius? Problem 2 – The luminosity, L, of a star is proportional to the square of its radius, R, and proportional to its surface temperature, T, to the fourth power. What is the equation for L if the proportionality constant is C? Problem 3 – The thickness of a planetary atmosphere, H, is proportional to temperature, T, and inversely proportional to the product of its molecular mass, m, and the local acceleration of gravity, g. What is the equation for H if the constant of proportionality is k? Problem 4 – The temperature of a planet, T, to the fourth power is proportional to the luminosity, L, of the star that it orbits, and inversely proportional to the square of its distance from its star, D. -

18. Mapping the Universe the Local Group: Over 30 Galaxies
Astronomy 242: Foundations of Astrophysics II 18. Mapping the Universe The Local Group: Over 30 Galaxies two large spirals with satellites one smaller spiral many dwarf elliptical and irregular galaxies Local Group The M81 Group M81 and M82 deep field The M81 Group in HI Tidal dwarfs in the M81 group The M81 Group M81 and M82 deep field The Virgo Cluster:: Over 1000 Galaxies! Distance: ~16 Mpc three massive elliptical galaxies many MW-sized galaxies The Virgo Cluster Abell 1689 Distance: ~754 Mpc Abell 1689: A Galaxy Cluster Makes Its Mark Abell 1689 in X-rays 7 keV Fe line (redshifted) X-ray Spectrum Abell 1689: A Galaxy Cluster Makes Its Mark Abell 1689 Central Galaxy Abell 1689: A Galaxy Cluster Makes Its Mark Abell 1689 Lensed galaxy in background Abell 1689: A Galaxy Cluster Makes Its Mark The Super-Galactic Plane Cosmography of the Local Universe Local Cosmography Pavo-Indus Super-Galactic Plane Perseus-Pisces Virgo Cluster 0 4000 8000 vr (km/s) Fornax Cluster Cosmography of the Local Universe The 2MASS Redshift Survey RESEARCH LETTER Extended Data Figure 3 | One of three orthogonal views that illustrate SGY 5 0 showing the region obscured by the plane of the Milky Way. As in the limits of the Laniakea supercluster. This SGX–SGY view at SGZ 5 0 Fig 2 in the main text, the orange contour encloses the inflowing streams, extends the scene shown in Fig. 2 with the addition of dark blue flow lines away hence, defines the limits of the LaniakeaThe Laniakea Supercluster supercluster of Galaxies containing the mass of from the Laniakea local basin of attraction, and also includes a dark swath at 1017 Suns and 100,000 large galaxies. -

Messier 58, 59, 60, 89, and 90, Galaxies in Virgo
Messier 58, 59, 60, 89, and 90, Galaxies in Virgo These are five of the many galaxies of the Coma-Virgo galaxy cluster, a prime hunting ground for galaxy observers every spring. Dozens of galaxies in this cluster are visible in medium to large amateur telescopes. This star hop includes elliptical galaxies M59, M60, and M89, and spiral galaxies M58 and M90. These galaxies are roughly 50 to 60 million light years away. All of them are around magnitude 10, and should be visible in even a small telescope. Start by finding the Spring Triangle, which consists of three widely- separated first magnitude stars-- Arcturus, Spica, and Regulus. The Spring Triangle is high in the southeast sky in early spring, and in the southwest sky by mid-Summer. (To get oriented, you can use the handle of the Big Dipper and "follow the arc to Arcturus"). For this star hop, look in the middle of the Spring Triangle for Denebola, the star representing the back end of Leo, the lion, and Vindemiatrix, a magnitude 2.8 star in Virgo. The galaxies of the Virgo cluster are found in the area between these two stars. From Vindemiatrix, look 5 degrees west and slightly south to find ρ (rho) Virginis, a magnitude 4.8 star that is easy to identify because it is paired with a slightly dimmer star just to its north. Center ρ in the telescope with a low-power eyepiece, and then just move 1.4 degrees north to arrive at the oval shape of M59. Continuing with a low-power eyepiece and using the chart below, you can take hops of less than 1 degree to find M60 to the east of M59, and M58, M89, and M90 to the west and north. -

General Disclaimer One Or More of the Following Statements May Affect This Document
General Disclaimer One or more of the Following Statements may affect this Document This document has been reproduced from the best copy furnished by the organizational source. It is being released in the interest of making available as much information as possible. This document may contain data, which exceeds the sheet parameters. It was furnished in this condition by the organizational source and is the best copy available. This document may contain tone-on-tone or color graphs, charts and/or pictures, which have been reproduced in black and white. This document is paginated as submitted by the original source. Portions of this document are not fully legible due to the historical nature of some of the material. However, it is the best reproduction available from the original submission. Produced by the NASA Center for Aerospace Information (CASI) N79-28092 (NASA-T"1-80294) A SEARCH FOR X-RAY FM13STON FROM RICH CLUSTF.'+S, F.XTFNt1Et'• F1ALOS AWIND CLUSTERS, AND SUPERCLUSTERS (NASA) 37 p rinclas HC AOl/ N F A01 CSCL 038 G3/90 29952 Technical Memorandum 80294 A Search for X- Ray Emission from Riche Clusters, Extended Halos around Clusters, and Superclusters S. H. Pravdo, E. A. Boldt, F. E. Marshall, J. Mc Kee, R. F. Mushotzky, B. W. Smith, and G. Reichert JUNE 1979 A Naticnal Aeronautics and Snn,^ Administration "` Goddard Space Flight Center Greenbelt, Maryland 20771 A SEARCH FOR X-RAY EMISSION FROM RICH CLUSTERS, EXTENDED HALOS AROUND CLUSTERS, ANU SUPERCLUSTERS • S.H Pravdo E A Boldt, F.E Marshall J. McKee R.F Mushotzky , B.W. -

Virgo the Virgin
Virgo the Virgin Virgo is one of the constellations of the zodiac, the group tion Virgo itself. There is also the connection here with of 12 constellations that lies on the ecliptic plane defined “The Scales of Justice” and the sign Libra which lies next by the planets orbital orientation around the Sun. Virgo is to Virgo in the Zodiac. The study of astronomy had a one of the original 48 constellations charted by Ptolemy. practical “time keeping” aspect in the cultures of ancient It is the largest constellation of the Zodiac and the sec- history and as the stars of Virgo appeared before sunrise ond - largest constellation after Hydra. Virgo is bordered by late in the northern summer, many cultures linked this the constellations of Bootes, Coma Berenices, Leo, Crater, asterism with crops, harvest and fecundity. Corvus, Hydra, Libra and Serpens Caput. The constella- tion of Virgo is highly populated with galaxies and there Virgo is usually depicted with angel - like wings, with an are several galaxy clusters located within its boundaries, ear of wheat in her left hand, marked by the bright star each of which is home to hundreds or even thousands of Spica, which is Latin for “ear of grain”, and a tall blade of galaxies. The accepted abbreviation when enumerating grass, or a palm frond, in her right hand. Spica will be objects within the constellation is Vir, the genitive form is important for us in navigating Virgo in the modern night Virginis and meteor showers that appear to originate from sky. Spica was most likely the star that helped the Greek Virgo are called Virginids. -

Angular Momentum of Galaxies in the Densest Environments: a FLAMES/GIRAFFE IFS Study of the Massive Cluster Abell 1689 at Z = 0
Astronomical Science Angular Momentum of Galaxies in the Densest Environments: A FLAMES/GIRAFFE IFS Study of the Massive Cluster Abell 1689 at z = 0.18 Francesco D’Eugenio1 of these empirical laws — alongside their bined with the collecting power of the Ryan C. W. Houghton1 very small scatter — imposes strong ESO Very Large Telescope (VLT), are the Roger L. Davies1 constraints on the structure and evolution ideal tools for this task. Elena Dalla Bontà2, 3 of ETGs (Bower et al., 1992). This makes them ideal testing grounds for any galaxy formation theory. Their study, important FLAMES/GIRAFFE observations of 1 Sub-department of Astrophysics, in its own right, is also fundamental Abell 1689 Department of Physics, University of for our understanding of the process of Oxford, United Kingdom structure formation in the Universe. Abell 1689, a massive galaxy cluster at 2 Dipartimento di Fisica e Astronomia redshift z = 0.183, has regular, concen- “G. Galilei”, Università degli Studi di The advent of integral field spectroscopy tric X-ray contours suggesting that it Padova, Italy (IFS) started a revolution in the study of is re laxed. Its X-ray luminosity outshines 3 INAF–Osservatorio Astronomico di ETGs. The SAURON survey discovered Coma by a factor of three, and Virgo Padova, Italy the existence of two kinematically distinct by over an order of magnitude. Its comov- classes of ETGs, slow and fast rotators ing distance is 740 Mpc, giving a scale (SRs and FRs, see Emsellem et al. [2007]) of 1 arcsecond per 3.0 kpc. Alongside its Early-type galaxies (ETGs) exhibit kine- and Cappellari et al. -

Stars and Galaxies
Stars and Galaxies STUDENT PAGE Se e i n g i n to t h e Pa S t A galaxy is a gravitationally bound system of stars, gas, and dust. Gal- We can’t travel into the past, but we axies range in diameter from a few thousand to a few hundred thou- can get a glimpse of it. Every sand light-years. Each galaxy contains billions (10 9) or trillions (1012) time we look at the Moon, for of stars. In this activity, you will apply concepts of scale to grasp the example, we see it as it was a distances between stars and galaxies. You will use this understanding little more than a second ago. to elaborate on the question, Do galaxies collide? That’s because sunlight reflected from the Moon’s surface takes a little more EX P LORE than a second to reach Earth. We see On a clear, dark night, you can see hundreds of bright stars. The next table the Sun as it looked about eight minutes shows some of the brightest stars with their diameters and distances from ago, and the other stars as they were a the Sun. Use a calculator to determine the scaled distance to each star few years to a few centuries ago. (how many times you could fit the star between itself and the Sun). Hint: And then there’s M31, the Androm- you first need to convert light-years and solar diameters into meters. One eda galaxy — the most distant object light-year equals 9.46 x 1015 meters, and the Sun’s diameter is 1.4 x 109 that’s readily visible to human eyes. -

'Virgo' from 'Urania's Mirror Or, a View of the Heavens' (1824)
Virgo 'Virgo' from 'Urania's Mirror or, a view of the Heavens' (1824) More exclusive content at InteractiveStars.com Your Personal Daily Horoscope - based on your exact date of birth Real Time, Personal Compatibility Horoscopes Soulmate Reports, Astrology Charts and much more click here to visit our website Contents Cover The Myths and Legends of Virgo The Stars The Sun in Astrology Mercury, Ruler of Virgo The Flowers of Virgo Copyright Information The Myths and Legends of Virgo The Great Goddess of the Harvest The winged Virgin, holding the palm branch and the Ear of Wheat which marks her brightest star, was worshipped as the great goddess of the harvest throughout the ancient world. The earth's bounty - flowers, fruits and fields of grain - were seen as her Beloved, whom she mourned at harvest time, when he was cut down in his prime. Having spent the winter in the underworld, he was reborn each spring and reunited with her. The origins of the cult of the Great Goddess, who was both virgin and mother, are prehistoric, but since the dawn of recorded history she has been associated with the constellation Virgo, through which the sun passes around harvest-time. Queen of the Stars Virgo is also the ancient Iraqi goddess Ishtar, Queen of the Stars, the lover of the corn god Tammuz, whose death she mourns every autumn, when he is cut down in his prime. Winter reigns during her journey to the underworld to bring him back, after which he reappears as the new, green corn each spring. Venus and Adonis The stories of Venus and Adonis, of Isis and Osiris, and of Cybele, the early Asiatic goddess in her turreted crown who loved Attis, are all variations on the theme.