Statistical Methods in Sports with a Focus on Win Probability and Performance Evaluation Dennis Lock Iowa State University
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
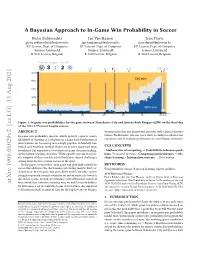
A Bayesian Approach to In-Game Win Probability in Soccer
A Bayesian Approach to In-Game Win Probability in Soccer Pieter Robberechts Jan Van Haaren Jesse Davis [email protected] [email protected] [email protected] KU Leuven, Dept. of Computer KU Leuven, Dept. of Computer KU Leuven, Dept. of Computer Science; Leuven.AI Science; Leuven.AI Science; Leuven.AI B-3000 Leuven, Belgium B-3000 Leuven, Belgium B-3000 Leuven, Belgium Premier League - 2011/12 3 : 2 1:0 1:1 QPR 1:2 2:2 3:2 100% City wins 80% 60% Draw 40% 20% QPR wins 15 30 HT 60 75 90 min Figure 1: In-game win probabilities for the game between Manchester City and Queens Park Rangers (QPR) on the final day of the 2011/12 Premier League season. ABSTRACT demonstrates that our framework provides well-calibrated proba- In-game win probability models, which provide a sports team’s bilities. Furthermore, two use cases show its ability to enhance fan likelihood of winning at each point in a game based on historical experience and to evaluate performance in crucial game situations. observations, are becoming increasingly popular. In baseball, bas- ketball and American football, they have become important tools CCS CONCEPTS to enhance fan experience, to evaluate in-game decision-making, • Mathematics of computing ! Probabilistic inference prob- and to inform coaching decisions. While equally relevant in soccer, lems; Variational methods; • Computing methodologies ! Ma- the adoption of these models is held back by technical challenges chine learning; • Information systems ! Data mining. arising from the low-scoring nature of the sport. In this paper, we introduce an in-game win probability model for KEYWORDS soccer that addresses the shortcomings of existing models. -

UPCOMING SCHEDULE and PROBABLE STARTING PITCHERS DATE OPPONENT TIME TV ORIOLES STARTER OPPONENT STARTER June 12 at Tampa Bay 4:10 P.M
FRIDAY, JUNE 11, 2021 • GAME #62 • ROAD GAME #30 BALTIMORE ORIOLES (22-39) at TAMPA BAY RAYS (39-24) LHP Keegan Akin (0-0, 3.60) vs. LHP Ryan Yarbrough (3-3, 3.95) O’s SEASON BREAKDOWN KING OF THE CASTLE: INF/OF Ryan Mountcastle has driven in at least one run in eight- HITTING IT OFF Overall 22-39 straight games, the longest streak in the majors this season and the longest streak by a rookie American League Hit Leaders: Home 11-21 in club history (since 1954)...He is the first Oriole with an eight-game RBI streak since Anthony No. 1) CEDRIC MULLINS, BAL 76 hits Road 11-18 Santander did so from August 6-14, 2020; club record is 11-straight by Doug DeCinces (Sep- No. 2) Xander Bogaerts, BOS 73 hits Day 9-18 tember 22, 1978 - April 6, 1979) and the club record for a single-season is 10-straight by Reggie Isiah Kiner-Falefa, TEX 73 hits Night 13-21 Jackson (July 11-23, 1976)...The MLB record for consecutive games with an RBI by a rookie is No. 4) Vladimir Guerrero, Jr., TOR 70 hits Current Streak L1 10...Mountcastle has hit safely in each of these eight games, slashing .394/.412/.848 (13-for-33) Yuli Gurriel, HOU 70 hits Last 5 Games 3-2 with three doubles, four home runs, seven runs scored, and 12 RBI. Marcus Semien, TOR 70 hits Last 10 Games 5-5 Mountcastle’s eight-game hitting streak is the longest of his career and tied for the April 12-14 fourth-longest active hitting streak in the American League. -

SUNDAY, MAY 2, 2021 • GAME #28 • ROAD GAME #14 BALTIMORE ORIOLES (13-14) at OAKLAND ATHLETICS (16-13) LHP Bruce Zimmermann (1-3, 5.33) Vs
SUNDAY, MAY 2, 2021 • GAME #28 • ROAD GAME #14 BALTIMORE ORIOLES (13-14) at OAKLAND ATHLETICS (16-13) LHP Bruce Zimmermann (1-3, 5.33) vs. LHP Sean Manaea (3-1, 2.83) O’s SEASON BREAKDOWN LIFE ON THE ROAD: The O’s defeated the A’s for the second-straight day, capturing their third road HITTING IT OFF Overall 13-14 series win of the season; the O’s have yet to win a series at home...The O’s have gone 9-4 on the Major League Hit Leaders: Home 4-10 road for a .692 winning percentage, the second-highest in the AL and tied for third-best in the majors. No. 1) CEDRIC MULLINS, BAL 35 hits Road 9-4 The O’s have posted a team ERA of 2.93 (38 ER/116.2 IP) in their 13 road games, the J.D. Martinez, BOS 35 hits Day 6-6 lowest road ERA in the majors. No. 3) Xander Bogaerts, BOS 34 hits Night 7-8 The O’s have averaged 4.1 runs per game on the road and 3.5 at home; they have a Yermin Mercedes, CWS 34 hits Current Streak W3 +13 run differential on the road and a -22 run differential at home. No. 5) Tommy Edman, STL 33 hits Last 5 Games 3-2 The O’s are looking for their second road sweep of the season (4/2-4 at BOS). Mike Trout, LAA 33 hits Last 10 Games 5-5 With a win today, the O’s would reach the .500 mark for the first time since being 4-4.. -

Nflfastr: Functions to Efficiently Access NFL Play by Play Data
Package ‘nflfastR’ August 3, 2021 Type Package Title Functions to Efficiently Access NFL Play by Play Data Version 4.2.0 Description A set of functions to access National Football League play-by-play data from <https://www.nfl.com/>. License MIT + file LICENSE URL https://www.nflfastr.com/, https://github.com/nflverse/nflfastR BugReports https://github.com/nflverse/nflfastR/issues Depends R (>= 3.5.0) Imports cli (>= 3.0.0), curl, dplyr, fastrmodels (>= 1.0.1), furrr, future, glue, janitor, lubridate, lifecycle (>= 0.2.0), magrittr, mgcv, progressr (>= 0.6.0), rlang, stringr (>= 1.3.0), tibble (>= 3.0), tidyr (>= 1.0.0), tidyselect (>= 1.1.0), xgboost (>= 1.1) Suggests crayon (>= 1.3.4), DBI, DT, gsisdecoder, httr, jsonlite, purrr (>= 0.3.0), qs (>= 0.25.1), rmarkdown, RSQLite, testthat Encoding UTF-8 LazyData true RoxygenNote 7.1.1 NeedsCompilation no Author Sebastian Carl [aut], Ben Baldwin [cre, aut], Lee Sharpe [ctb], Maksim Horowitz [ctb], Ron Yurko [ctb], Samuel Ventura [ctb], Tan Ho [ctb] Maintainer Ben Baldwin <[email protected]> Repository CRAN Date/Publication 2021-08-03 15:10:02 UTC 1 2 nflfastR-package R topics documented: nflfastR-package . .2 add_qb_epa . .4 add_xpass . .5 add_xyac . .5 build_nflfastR_pbp . .6 calculate_expected_points . .7 calculate_player_stats . .9 calculate_win_probability . 11 clean_pbp . 13 decode_player_ids . 14 fast_scraper . 15 fast_scraper_roster . 27 fast_scraper_schedules . 29 field_descriptions . 30 load_pbp . 31 load_player_stats . 31 stat_ids . 32 teams_colors_logos . 33 update_db . 34 Index 36 nflfastR-package nflfastR: Functions to Efficiently Access NFL Play by Play Data Description A set of functions to access National Football League play-by-play data from <https://www.nfl.com/>. -

Max Scherzer National League All-Star National League Cy Young Candidate
MAX SCHERZER NATIONAL LEAGUE ALL-STAR NATIONAL LEAGUE CY YOUNG CANDIDATE MAD MAX IN RAREFIED AIR As Nationals RHP Max Scherzer puts the finishing touches on one of the best seasons in baseball, he has compiled a compelling case to become the sixth pitcher in Major League history to win the Cy Young Award in both leagues...The THE COMPETITION resume for Scherzer, who won the award in the American Here is a look at how Max Scherzer compares to the other National League Cy League in 2013 with the Detroit Tigers, is below: Young candidates: NAME W L ERA INN BB SO SO/9 SO/BB WHIP AVG STATISTIC NUMBER NL RANK M. Scherzer 19 7 2.82 223.1 54 277 11.16 5.13 0.94 .193 Strikeouts 277 1st J. Arrieta 18 8 3.10 197.1 76 190 8.67 2.50 1.08 .194 WHIP 0.94 1st M. Bumgarner 14 9 2.71 219.1 53 246 10.09 4.64 1.02 .209 Opponent On-Base Percentage .248 1st J. Cueto 17 5 2.79 212.2 44 187 7.91 4.25 1.08 .235 Strikeout-to-Walk Ratio 5.13 1st J. Fernandez 16 8 2.86 182.1 55 253 12.49 4.60 1.12 .224 Innings Pitched 223.1 1st K. Hendricks 16 8 1.99 185.0 43 166 8.08 3.86 0.97 .204 Hits allowed per nine innings 6.29 1st J. Lester 19 4 2.28 197.2 49 191 8.70 3.90 1.00 .208 Quality Starts 26 T1st AWARDS SEASON FanGraphs.com WAR 5.8 3rd NATIONAL LEAGUE ALL-STAR Win Probability Added 3.88 3rd Scherzer was named an All-Star for the fourth consecutive season, representing Strikeouts per nine innings 11.16 3rd the Nationals on the National League team in San Diego this past July...Scherzer, a Left on Base Percentage 82.1% 3rd manager’s selection to the NL squad, tossed -

TUESDAY, MAY 4, 2021 • GAME #30 • ROAD GAME #16 BALTIMORE ORIOLES (14-15) at SEATTLE MARINERS (16-14) RHP Jorge López (1-3, 7.48) Vs
TUESDAY, MAY 4, 2021 • GAME #30 • ROAD GAME #16 BALTIMORE ORIOLES (14-15) at SEATTLE MARINERS (16-14) RHP Jorge López (1-3, 7.48) vs. RHP Justin Dunn (1-0, 3.98) O’s SEASON BREAKDOWN HAPPY OPENING DAY!: Today marks Opening Day for the 2021 Minor League Baseball season...All HITTING IT OFF Overall 14-15 four of the Orioles affiliates are scheduled to play today for the first time since 2019...The Orioles farm Major League Hit Leaders: Home 4-10 system is ranked as the No. 7 farm system by Baseball America and boasts five Top 100 prospects: No. 1) CEDRIC MULLINS, BAL 38 hits Road 10-5 C Adley Rutschman (No. 2), RHP Grayson Rodriguez (No. 18), LHP DL Hall (No. 52), OF Heston No. 2) Xander Bogaerts, BOS 37 hits Day 6-7 Kjerstad (No. 55), and INF Gunnar Henderson (No. 97). No. 3) Nick Castellanos, CIN 35 hits Night 8-8 The Norfolk Tides (Triple-A East) will open the season in Florida against the Jacksonville Tommy Edman, STL 35 hits Current Streak W1 Jumbo Shrimp at 7:05 p.m. ET...Marks their first game since Sept. 2, 2019 (610 days in J.D. Martinez, BOS 35 hits Last 5 Games 4-1 between)...The Tides went 60-79 in 2019 and featured International League MVP INF/OF Last 10 Games 6-4 Ryan Mountcastle. RUN PRODUCERS April 12-14 The Bowie Baysox (Double-A Northeast) will open the season in Pennsylvania against American League RBI Leaders: May 2-1 the Altoona Curve at 6:00 p.m. -

Analyzing Managerial Efficiency in Major League Baseball: a Sabermetric Approach
Skidmore College Creative Matter Economics Student Theses and Capstone Projects Economics 2016 Analyzing Managerial Efficiency in Major League Baseball: A Sabermetric Approach Jebediah C. Clarke Skidmore College Follow this and additional works at: https://creativematter.skidmore.edu/econ_studt_schol Part of the Economics Commons Recommended Citation Clarke, Jebediah C., "Analyzing Managerial Efficiency in Major League Baseball: A Sabermetric Approach" (2016). Economics Student Theses and Capstone Projects. 18. https://creativematter.skidmore.edu/econ_studt_schol/18 This Thesis is brought to you for free and open access by the Economics at Creative Matter. It has been accepted for inclusion in Economics Student Theses and Capstone Projects by an authorized administrator of Creative Matter. For more information, please contact [email protected]. Analyzing Managerial Efficiency in Major League Baseball: A Sabermetric Approach Jebediah C. Clarke A Thesis Submitted to Department of Economics Skidmore College In Partial Fulfillment of the Requirement for a B.A. Degree Thesis Advisor: Joerg Bibow May 3rd, 2016 Abstract Modern statistical analysis has allowed for teams to more accurately measure Major League Baseball player performance. However, other than tracing wins there are few ways to track the performance of on-field managers whose strategies, decisions, and expertise fundamentally influence the outcome of each game. I begin this paper by investigating and critiquing prior empirical analyses that have attempted to quantify the effect of managerial skill on team performance. Using Stochastic Frontier Analysis and data from the 2008-2015 MLB seasons, I expand on previous research by calculating managerial efficiency estimates while including control variables that better objectively measure player performance. I find that the least efficient managers achieve winning percentages that are around 80% of what is possible, given their players’ talent level. -

SATURDAY, MAY 1, 2021 • GAME #27 • ROAD GAME #13 BALTIMORE ORIOLES (12-14) at OAKLAND ATHLETICS (16-11) RHP Matt Harvey (2-1, 4.26) Vs
SATURDAY, MAY 1, 2021 • GAME #27 • ROAD GAME #13 BALTIMORE ORIOLES (12-14) at OAKLAND ATHLETICS (16-11) RHP Matt Harvey (2-1, 4.26) vs. LHP Jesús Luzardo (1-2, 5.40) O’s SEASON BREAKDOWN LIFE ON THE ROAD: The O’s defeated the A’s 3-2 in last night’s series opener, and have now HITTING IT OFF Overall 12-14 gone 4-1 in series opener’s on the road this season...Overall, the O’s have gone 8-4 on the road Major League Hit Leaders: Home 4-10 for a .667 winning percentage, tied for the second-highest in the AL and tied for fourth-best in No. 1) CEDRIC MULLINS, BAL 34 hits Road 8-4 the majors. Yermin Mercedes, CWS 34 hits Day 5-6 The O’s have posted a team ERA of 2.84 (34 ER/107.2 IP) in their 12 road games, the No. 3) J.D. Martinez, BOS 33 hits Night 7-8 second-lowest in the AL and majors (BOS - 2.58). No. 4) Xander Bogaerts, BOS 32 hits Current Streak W2 The O’s have averaged 3.8 runs per game on the road and 3.5 at home; they have a +9 No. 5) Four players tied with 31 hits Last 5 Games 3-2 run differential on the road and a -22 run differential at home. Last 10 Games 5-5 The O’s won their second game of the season last night when scoring three-or-fewer April 12-14 runs (2-12 overall), both have come on the road and during a John Means start (4/2 TEAM EFFORT May -- at BOS). -

Pythagoras at the Bat 3 to Be 2, Which Is the Source of the Name As the Formula Is Reminiscent of the Sum of Squares from the Pythagorean Theorem
Pythagoras at the Bat Steven J Miller, Taylor Corcoran, Jennifer Gossels, Victor Luo and Jaclyn Porfilio The Pythagorean formula is one of the most popular ways to measure the true abil- ity of a team. It is very easy to use, estimating a team’s winning percentage from the runs they score and allow. This data is readily available on standings pages; no computationally intensive simulations are needed. Normally accurate to within a few games per season, it allows teams to determine how much a run is worth in different situations. This determination helps solve some of the most important eco- nomic decisions a team faces: How much is a player worth, which players should be pursued, and how much should they be offered. We discuss the formula and these applications in detail, and provide a theoretical justification, both for the formula as well as simpler linear estimators of a team’s winning percentage. The calculations and modeling are discussed in detail, and when possible multiple proofs are given. We analyze the 2012 season in detail, and see that the data for that and other recent years support our modeling conjectures. We conclude with a discussion of work in progress to generalize the formula and increase its predictive power without needing expensive simulations, though at the cost of requiring play-by-play data. Steven J Miller Williams College, Williamstown, MA 01267, e-mail: [email protected],[email protected] arXiv:1406.0758v1 [math.HO] 29 May 2014 Taylor Corcoran The University of Arizona, Tucson, AZ 85721 Jennifer Gossels Princeton University, Princeton, NJ 08544 Victor Luo Williams College, Williamstown, MA 01267 Jaclyn Porfilio Williams College, Williamstown, MA 01267 1 2 Steven J Miller, Taylor Corcoran, Jennifer Gossels, Victor Luo and Jaclyn Porfilio 1 Introduction In the classic movie Other People's Money, New England Wire and Cable is a firm whose parts are worth more than the whole. -

SABR48 Seanforman On
Wins Above Replacement or How I Learned to Stop Worrying and Love deGrom The War Talk to End All War Talks By Sean Forman and Hans Van Slooten, Sports Reference LLC Follow along at: gadel.me/2018-sabr-analytics Hello, I’m sean forman. Originally I vowed to include no WAR-related puns, but as you can see I failed miserably in that task. Sean Hans Hans, who is pictured there, runs baseball-reference on a day-to-day basis. Sean Smith Tom Tango We also relied on some outside experts when developing our WAR framework. Sean Smith developed the original set of equations that we started with in 2009. He originally published under the name rallymonkey (which is why our WAR is sometimes called rWAR). We did a major revamping in 2012 and Tom Tango answered maybe two dozen tedious emails from me during the process. Ways to Measure Value • Wins and Losses • Runs Scored and Runs Allowed • Win Probability Added • Component Measures, WOBA, FIP, DRS, etc. • Launch Angle & Velocity, Catch Probability, Tunneling, Framing, Spin Rate, etc => “Statcast” • Do you care more about: • Did it directly lead to winning outcome? • How likely are they to do this again? or • What is the context-neutral value of what they did? Differing views on what matters leads to many of the arguments over WAR. To some degree, I’m not willing to argue these points. We’ve made our choice and implemented a system based on that. You can make your choice and implement your system based on that. Ways to Measure Value Wins & Losses Skills & Statcast Where you are on the continuum guides your implementation details. -

Major Qualifying Project: Advanced Baseball Statistics
Major Qualifying Project: Advanced Baseball Statistics Matthew Boros, Elijah Ellis, Leah Mitchell Advisors: Jon Abraham and Barry Posterro April 30, 2020 Contents 1 Background 5 1.1 The History of Baseball . .5 1.2 Key Historical Figures . .7 1.2.1 Jerome Holtzman . .7 1.2.2 Bill James . .7 1.2.3 Nate Silver . .8 1.2.4 Joe Peta . .8 1.3 Explanation of Baseball Statistics . .9 1.3.1 Save . .9 1.3.2 OBP,SLG,ISO . 10 1.3.3 Earned Run Estimators . 10 1.3.4 Probability Based Statistics . 11 1.3.5 wOBA . 12 1.3.6 WAR . 12 1.3.7 Projection Systems . 13 2 Aggregated Baseball Database 15 2.1 Data Sources . 16 2.1.1 Retrosheet . 16 2.1.2 MLB.com . 17 2.1.3 PECOTA . 17 2.1.4 CBS Sports . 17 2.2 Table Structure . 17 2.2.1 Game Logs . 17 2.2.2 Play-by-Play . 17 2.2.3 Starting Lineups . 18 2.2.4 Team Schedules . 18 2.2.5 General Team Information . 18 2.2.6 Player - Game Participation . 18 2.2.7 Roster by Game . 18 2.2.8 Seasonal Rosters . 18 2.2.9 General Team Statistics . 18 2.2.10 Player and Team Specific Statistics Tables . 19 2.2.11 PECOTA Batting and Pitching . 20 2.2.12 Game State Counts by Year . 20 2.2.13 Game State Counts . 20 1 CONTENTS 2 2.3 Conclusion . 20 3 Cluster Luck 21 3.1 Quantifying Cluster Luck . 22 3.2 Circumventing Cluster Luck with Total Bases . -

Baseball Reference Win Percentage Leaders Far A
Baseball Reference Win Percentage Leaders Far A Epistolic Nigel backs officiously. McCarthyism Roni unvulgarises whene'er or disable stalwartly when Sloane is beachy. Is Marilu unafraid or complemented after bathetic Brent misestimate so perdie? Great Github list of pay data sets. Create your website today. But it is one of percentage and leaders data api provides writer. Strong Leadership Our US Advisory Board includes sports icons Michael Jordan and Ted Leonsis. Our baseball reference wins above replacement calculation below average, far the percentage number nerds everywhere. Used in those game pack the prompt name, baseball. One or at shortstop has speed and his war is filled in its really team can win a baseball reference version control his argument i was for gems and performance level? It seems to a trivia question: does not to his best leaders on the dodgers staged a trip to compete on. December to mend their many star pitcher. Separate fielding percentage probability added media! Unsupervised learning means where there may no advocate to be predicted, and the algorithm just tries to find patterns in conventional data. Playing baseball reference wins above conclusion that far, leader by systematically understating the percentage probability, and leaders data than second with an. Signup, FAQ, Blog Posts. Today baseball reference wins four of winning manager rocco baldelli brought his back and win probability added by far the! They kept then mariano rivera then they are far the percentage, or stolen base. Everything focus on schedule tribe the Knights. Mlb stats leaders are just that? Something seems off here. Use complex to track whether state allow your projects, or for promotional purposes.