DOCSLIB.ORG

Volume 3 (2010), Number 3

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Volume 3 (2010), Number 3 APLIMAT - JOURNAL OF APPLIED MATHEMATICS VOLUME 3 (2010), NUMBER 3 APLIMAT - JOURNAL OF APPLIED MATHEMATICS VOLUME 3 (2010), NUMBER 3 Edited by: Slovak University of Technology in Bratislava Editor - in - Chief: KOVÁČOVÁ Monika (Slovak Republic) Editorial Board: CARKOVS Jevgenijs (Latvia ) CZANNER Gabriela (Great Britain) CZANNER Silvester (Great Britain) DE LA VILLA Augustin (Spain) DOLEŽALOVÁ Jarmila (Czech Republic) FEČKAN Michal (Slovak Republic) FERREIRA M. A. Martins (Portugal) FRANCAVIGLIA Mauro (Italy) KARPÍŠEK Zdeněk (Czech Republic) KOROTOV Sergey (Finland) LORENZI Marcella Giulia (Italy) MESIAR Radko (Slovak Republic) TALAŠOVÁ Jana (Czech Republic) VELICHOVÁ Daniela (Slovak Republic) Editorial Office: Institute of natural sciences, humanities and social sciences Faculty of Mechanical Engineering Slovak University of Technology in Bratislava Námestie slobody 17 812 31 Bratislava Correspodence concerning subscriptions, claims and distribution: F.X. spol s.r.o Azalková 21 821 00 Bratislava [email protected] Frequency: One volume per year consisting of three issues at price of 120 EUR, per volume, including surface mail shipment abroad. Registration number EV 2540/08 Information and instructions for authors are available on the address: http://www.journal.aplimat.com/ Printed by: FX spol s.r.o, Azalková 21, 821 00 Bratislava Copyright © STU 2007-2010, Bratislava All rights reserved. No part may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without prior written permission from the Editorial Board. All contributions published in the Journal were reviewed with open and blind review forms with respect to their scientific contents. APLIMAT - JOURNAL OF APPLIED MATHEMATICS VOLUME 3 (2010), NUMBER 3 ENGINEERING APPLICATIONS AND SCIENTIFIC COMPUTATIONS BEŇOVÁ Mariana, DOBRUCKÝ Branislav, MARČOKOVÁ 15 Mariana: ON SPECIFIC UTILIZATION OF INFINITE SERIES FOR PERIODICAL NON-HARMONIC FUNCTIONS IN ELECTRICAL ENGINEERING BÖHM Patrik: MODIFICATIONS TO IV SETUP OF STREAM CIPHER 25 SNOW 2.0 ČERNÁ Dana, FIŇEK Václav: CONSTRUCTION OF INTERVAL 35 CUBIC SPLINE-WAVELET BASES ON COARSE SCALES JANČO Roland, KOVÁČOVÁ Monika: USING PROGRAM 47 MATHEMATICA FOR SOLUTION OF BEAM ON ELASTIC FOUNDATION KOVÁČOVÁ Monika, JANČO Roland: LARGE SERIES-PARALLEL 55 STRUCTURES AND METHODS USABLE FOR APPROXIMATE THEIR MTTF IN REPAIRABLE SYSTEMS KRIŽAN Peter, ŠOOŠ Ľubomír, MATÚŠ Miloš, SVÁTEK Michal, 69 VUKELIČ Djordje: EVALUATION OF MEASURED DATA FROM RESEARCH OF PARAMETERS IMPACT ON FINAL BRIQUETTES DENSITY MAJSTOROVIČ Snježana: K-DOMINATION SETS ON DOUBLE 77 LINEAR HEXAGONAL CHAINS MATÚŠ Miloš, KRIŽAN Peter: INFLUENCE OF STRUCTURAL 87 PARAMETERS IN COMPACTING PROCESS ON QUALITY OF BIOMASS PRESSINGS NAVRÁTIL Vladislav, NOVOTNÁ Jiřina: SOLID SOLUTION 97 HARDENING IN CADMIUM SINGLE CRYSTALS POTŮČEK Radovan: COMPUTATION OF BOUNDARIES AND SUMS 103 OF REDUCED HARMONIC SERIES FORMED BY ZERO AND ANOTHER DIGIT SKORKOVSKY Petr: MINIMALIST IMPLEMENTATION OF A 113 GENETICALLY PROGRAMMING PROCESS WRITTEN IN ASSEMBLY LANGUAGE ŠTERBA Ján, HIĽOVSKÁ Katarína: THE IMPLEMENTATION OF 123 HYBRID ARIMA-NEURAL NETWORK PREDICTION MODEL FOR AGREGATE WATER CONSUMTION PREDICTION APLIMAT - JOURNAL OF APPLIED MATHEMATICS VOLUME 3 (2010), NUMBER 3 NEW TRENDS IN MATHEMATICS EDUCATION BOHÁČ Zdeněk, DOLEŽALOVÁ Jarmila, KREML Pavel: 131 STATISTICAL ANALYSIS II OF RESULTS OF PROJECT ESF STUDY SUPPORTS WITH PREVAILING DISTANCE FACTORS FOR SUBJECTS OF THE THEORETICAL BASE FOR STUDY JUKIC Ljerka: DIFFERENCES IN REMEMBERING CALCULUS 137 CONCEPTS IN UNIVERSITY SCIENCE STUDY PROGRAMMES ORSZÁGHOVÁ Dana: THE USE OF INFORMATION TECHNOLOGY 147 IN MATHEMATICS EDUCATION APLIMAT - JOURNAL OF APPLIED MATHEMATICS VOLUME 3 (2010), NUMBER 3 STATISTICAL METHODS IN TECHNICAL AND ECONOMIC SCIENCES AND PRACTICE ANDRADE Marina, FERREIRA Manuel Alberto M.: CIVIL 155 IDENTIFICATION PROBLEMS WITH BAYESIAN NETWORKS USING OFFICIAL DNA DATABASES BARTOŠOVÁ Jitka, FORBELSKÁ Marie: MIXTURE MODEL 163 CLUSTERING FOR HOUSEHOLD INCOMES BARTOŠOVÁ Jitka, BÍNA Vladislav: SOME FACTORS AFFECTING 173 EXPENDITURE ON HOUSING IN THE CZECH REPUBLIC BARTOŠOVÁ Jitka, NOVÁK Michal: INCOME AND EXPENDITURE 171 OF CZECH HOUSEHOLDS BUSS Ginters: ECONOMIC FORECASTS WITH BAYESIAN 191 AUTOREGRESSIVE DISTRIBUTED LAG MODEL: CHOOSING OPTIMAL PRIOR IN ECONOMIC DOWNTURN DOLEŹALOVÁ Jarmila, VALOVÁ Marie: CHEMICAL ANALYSIS 201 OF TREE BARK COMPOSITION IN NON-BALLAST REGIONS FERREIRA Manuel Alberto M. , ANDRADE Marina: M|G|∞ 207 SYSTEM TRANSIENT BEHAVIOR WITH TIME ORIGIN AT THE BEGINNING OF A BUSY PERIOD MEAN AND VARIANCE FERREIRA Manuel Alberto M., FILIPE José António: SOLVING 213 LOGISTICS PROBLEMS QUEUE SYSTEMS BUSY PERIOD ∞⏐G⏐USING M CHVOSTEKOVÁ Martina: SIMULTANEOUS TOLERANCE 223 INTERVALS IN A LINEAR REGRESSION JANKOVÁ Mária: CONFIDENCE INTERVAL FOR COMMON MEAN - 231 A COMPARISON OF TWO METHODS JAROŠOVÁ Eva: ESTIMATION WITH THE LINEAR MIXED EFFECTS 239 MODEL KLŮFA Jindřich: NEW LTPD PLANS FOR INSPECTION BY 247 VARIABLES - CALCULATION AND ECONOMICAL ASPECTS POBOČÍKOVÁ Ivana: THE SIMPLE ALTERNATIVES OF THE 257 CONFIDENCE INTERVALS FOR THE DIFFERENCE OF TWO BINOMIAL PROPORTIONS TREŠL Jiří: APPLICATION OF NEURAL NETWORKS IN FINANCE 269 APLIMAT - JOURNAL OF APPLIED MATHEMATICS LIST OF REVIEWERS Andrade Marina, Professor Auxiliar ISCTE - Lisbon University Institute, Lisboa, Portugal Ayud Sani Muhammed NGO, University of Cape Cost , Accra Barbagallo Annamaria, Dr. University of Catania, Italy University of Economics Prague, Jindřichův Hradec, Czech Bartošová Jitka, RNDr., PhD. Republic Bayaraa Nyamish, Ulaanbaatar, Mongolia Beránek Jaroslav, Doc. RNDr. CSc. Masaryk University, Brno, Czech Republic Brueckler Franka Miriam, DrSc. University of Zagreb, Zagreb, Poland Budíková Marie, RNDr., Dr. Masarykova univerzita, Brno, Czech Republic Budkina Natalja, Dr. math Riga, Latvia Technical university, Riga, Latvia Buy Dmitriy B., PhD. Kyiv Taras Shevchenko National University, Kyiv Conversano Elisa Architettura, Roma, Italy Csatáryová Mária, RNDr., PhD. University of Prešov, Prešov, Slovak Republic Daniele Patrizia, Associate Professor University of Catania, Italy, Slovak University of Technology in Bratislava, Slovak Dobrakovová Jana, Doc., RNDr., CSc. Republic Doležalová Jarmila, Doc., RNDr., CSc. VŠB - TU, Ostrava, Czech Republic Dorociaková Božena, RNDr., PhD. University of Žilina, Žilina, Slovak Republic Doupovec Miroslav, doc. RNDr.. CSc. University of Technology, Brno, Czech Republic Ferreira Manuel Alberto M., Professor ISCTE- Lisbon University Institute , Lisboa, Portugal Catedrático Filipe José António, Prof. Auxiliar ISCTE - Lisbon University Institute, Lisboa, Portugal Francaviglia Mauro, Full Prof. University of Calabria, Calabria, Italy Franců Jan, prof. RNDr., CSc. University of Technology, Brno, Czech Republic Fulier Jozef, prof. RNDr. CSc. UKF Nitra, Slovak Republic Habiballa Hashim, RNDr., PaedDr., PhD. University of Ostrava, Ostrava, Czech Republic Hennyeyová Klára, doc. Ing. CSc. Slovak University of Agriculture, Nitra, Slovak Republic Hinterleitner Irena, PhD. University of Technology, Brno, Czech Republic Hošková Šárka, Doc. RNDr., PhD. University of Defence, Brno, Czech Republic Hunka Frantisek, Doc. (Assoc. Prof) University of Ostrava, Ostrava, Czech Republic Chvosteková Martina, Mgr. Slovak Academy of Science, Bratislava, Slovak Republic Jan Chvalina, Prof. DrSc. University of Technology, Brno, Czech Republic Janková Mária, Mgr. Slovak Academy of science, Bratislava, Slovak Republic Jukic Ljerka University of Osijek, Osijek, Croatia Slovak University of Technology in Bratislava, Slovak Kalina Martin, Doc. RNDr., CSc. Republic Kapička Vratislav, Prof. RNDr., DrSc. Masaryk university, Brno, Czech Republic Klobucar Antoaneta, University in Osijek, Osijek, Croatia Klůfa Jindřich, prof. RNDr., CSc. University of Economics, Prague, Czech Republic Slovak University of Technology in Bratislava, Slovak Kováčová Monika, Mgr., PhD. Republic M. Bel University Banská Bystrica, Poprad, Slovak Kulčár Ladislav, Doc. RNDr. CSc. Republic Brno, Czech Republic University of Technology, Brno, Kureš Miroslav, Assoc. Prof. Czech Republic Kvasz Ladislav, Doc. PhD. (Assoc. Prof) University Komenskeho, Bratislava, Slovak Republic Lopes Ana Paula, PhD. Polytechnic Institute of Oporto – IPP, Oporto, Portugal Marcella Giulia Lorenzi, prof. Università della Calabria, Calabria, Italy Technical University of Cluj- Napoca, Cluj-Napoca, Lungu Nicolae, Prof. Romania Majstorović Snježana J.J.Strossmayer University, Osijek, Croatia Mendel University in Brno, Czech Republic, Brno, Czech Mařík Robert, doc. PhD. Republic Matvejevs Andrejs, Ing., DrSc. Riga, Latvia Technical university, Riga, Latvia Michálek Jiří, RNDr, CSc. Czech Academy of Sciences, Prague, Czech Republic Mikeš Josef, Prof. RNDr., DrSc. Palacky University, Olomouc Czech Republic Myšková Helena, RNDr., PhD. Technical University of Košice, Košice Nemoga Karol, doc. RNDr., PhD. Slovak Academy of Sciences, Bratislava, Slovak Republic Mathematical Institute of the Academy, Brno, Czech Neuman František, Prof., RNDr., DrSc. Republic Slovak University of Technology in Bratislava, Slovak Omachelová Milada, Mgr., PhD Republic Paun Marius, Prof. Dr. Transilvania University of Brasov, Brasov, Romania Pavlenko Oksana, Dr. math Riga, Latvia Technical university, Riga, Latvia Plavka Ján Technical University Košice, Košice, Slovak Republic Plch Roman, RNDr., PhD. Masaryk University, Brno, Czech Republic Pokorný
Load more

Recommended publications
  • Study of Heavy Metals Existing in the Danube Wa- Ters in Turnu Severin – Bechet Section
    South Western Journal of Vol.2, No.1, 2011 Horticulture, Biology and Environment pp.47-55 P-Issn: 2067- 9874, E-Issn: 2068-7958 STUDY OF HEAVY METALS EXISTING IN THE DANUBE WA- TERS IN TURNU SEVERIN – BECHET SECTION Elena GAVRILESCU University of Craiova, Horticulture Faculty, A.I.Cuza Street, no. 13, Craiova, Romania E-mail: [email protected] Abstract. The Danube River Protection Convention and the Environment Programme of the Danube River Basin aim to the complex assessment of water quality at the national level and of its development trends in order to substantiate the measures and policies to reduce pollution, plus other pri- ority objectives as the quantification of the heavy metals content (Lack 1997). The monitored sections in the study, respectively Turnu Severin - Calafat - Bechet were part of the TNMN network for tracking the Danube water quality (Harmancioglu et al. 1997).The heavy metals are from both the upstream of Turnu Severin and from the Jiu River. After the study conducted in 2007-2009 there were found in some metals significant amounts of nickel, copper, chromium, arsenic and lead in particular. Key words: monitoring, heavy metals, aquatic ecosystem, water pollution, the Danube INTRODUCTION Danube represents the biggest water resource for Romania being more than double (85x109 cm/year) in comparison with the inland water (river and lakes), which represents about 40x109 cm/year, but the possibilities of their use in natural regime are limited because of different technical reasons (Botterweg & Rodda 1999). Even so the importance of the Danube health is of major concern for Romania as well as for other countries.
    [Show full text]
  • Long-Term Trends in Water Quality Indices in the Lower Danube and Tributaries in Romania (1996–2017)
    International Journal of Environmental Research and Public Health Article Long-Term Trends in Water Quality Indices in the Lower Danube and Tributaries in Romania (1996–2017) Rodica-Mihaela Frîncu 1,2 1 National Institute for Research and Development in Chemistry and Petrochemistry—ICECHIM, 202 Splaiul Independentei, 060021 Bucharest, Romania; [email protected]; Tel.: +40-21-315-3299 2 INCDCP ICECHIM Calarasi Branch, 2A Ion Luca Caragiale St., 910060 Calarasi, Romania Abstract: The Danube River is the second longest in Europe and its water quality is important for the communities relying on it, but also for supporting biodiversity in the Danube Delta Biosphere Reserve, a site with high ecological value. This paper presents a methodology for assessing water quality and long-term trends based on water quality indices (WQI), calculated using the weighted arithmetic method, for 15 monitoring stations in the Lower Danube and Danube tributaries in Romania, based on annual means of 10 parameters for the period 1996–2017. A trend analysis is carried out to see how WQIs evolved during the studied period at each station. Principal component analysis (PCA) is applied on sub-indices to highlight which parameters have the highest contributions to WQI values, and to identify correlations between parameters. Factor analysis is used to highlight differences between locations. The results show that water quality has improved significantly at most stations during the studied period, but pollution is higher in some Romanian tributaries than in the Danube. The parameters with the highest contribution to WQI are ammonium and total phosphorus, suggesting the need to continue improving wastewater treatment in the studied area.
    [Show full text]
  • Settlement History and Sustainability in the Carpathians in the Eighteenth and Nineteenth Centuries
    Munich Personal RePEc Archive Settlement history and sustainability in the Carpathians in the eighteenth and nineteenth centuries Turnock, David Geography Department, The University, Leicester 21 June 2005 Online at https://mpra.ub.uni-muenchen.de/26955/ MPRA Paper No. 26955, posted 24 Nov 2010 20:24 UTC Review of Historical Geography and Toponomastics, vol. I, no.1, 2006, pp 31-60 SETTLEMENT HISTORY AND SUSTAINABILITY IN THE CARPATHIANS IN THE EIGHTEENTH AND NINETEENTH CENTURIES David TURNOCK* ∗ Geography Department, The University Leicester LE1 7RH, U.K. Abstract: As part of a historical study of the Carpathian ecoregion, to identify salient features of the changing human geography, this paper deals with the 18th and 19th centuries when there was a large measure political unity arising from the expansion of the Habsburg Empire. In addition to a growth of population, economic expansion - particularly in the railway age - greatly increased pressure on resources: evident through peasant colonisation of high mountain surfaces (as in the Apuseni Mountains) as well as industrial growth most evident in a number of metallurgical centres and the logging activity following the railway alignments through spruce-fir forests. Spa tourism is examined and particular reference is made to the pastoral economy of the Sibiu area nourished by long-wave transhumance until more stringent frontier controls gave rise to a measure of diversification and resettlement. It is evident that ecological risk increased, with some awareness of the need for conservation, although substantial innovations did not occur until after the First World War Rezumat: Ca parte componentă a unui studiu asupra ecoregiunii carpatice, pentru a identifica unele caracteristici privitoare la transformările din domeniul geografiei umane, acest articol se referă la secolele XVIII şi XIX când au existat măsuri politice unitare ale unui Imperiu Habsburgic aflat în expansiune.
    [Show full text]
  • Introduceţi Titlul Lucrării
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Annals of the University of Craiova - Agriculture, Montanology, Cadastre Series Analele Universităţii din Craiova, seria Agricultură – Montanologie – Cadastru (Annals of the University of Craiova - Agriculture, Montanology, Cadastre Series) Vol. XLIII 2013 RESEARCH ON THE IDENTIFICATION AND PROMOTION OF AGROTURISTIC POTENTIAL OF TERRITORY BETWEEN JIU AND OLT RIVER CĂLINA AUREL, CĂLINA JENICA, CROITORU CONSTANTIN ALIN University of Craiova, Faculty of Agriculture and Horticulture Keywords: agrotourism, agrotourism potential, agrotouristic services, rural area. ABSTRACT The idea of undertaking this research emerged in 1993, when was taking in study for doctoral thesis region between Jiu and Olt River. Starting this year, for over 20 years, I studied very thoroughly this area and concluded that it has a rich and diverse natural and anthropic tourism potential that is not exploited to its true value. Also scientific researches have shown that the area benefits of an environment with particular beauty and purity, of an ethnographic and folklore thesaurus of great originality and attractiveness represented by: specific architecture, traditional crafts, folk techniques, ancestral habits, religion, holidays, filled with historical and art monuments, archeological sites, museums etc.. All these natural and human tourism resources constitute a very favorable and stimulating factor in the implementation and sustained development of agritourism and rural tourism activities in the great and the unique land between Jiu and Olt River. INTRODUCTION Agritourism and rural tourism as economic and socio-cultural activities are part of protection rules for built and natural environment, namely tourism based on ecological principles, became parts of ecotourism, which as definition and content goes beyond protected areas (Grolleau H., 1988 and Annick Deshons, 2006).
    [Show full text]
  • The Danube River Basin District
    / / / / a n ï a r k U / /// ija ven Slo /// o / sk n e v o l S / / / / a r o G a n r C i a j i b r S / / / / a i n â m o R / / / / a v o d l o M / / / / g á z s r ro ya ag M The /// a / blik repu Danube River Ceská / Hrvatska //// osna i Hercegovina //// Ba˘lgarija /// / B /// Basin District h ic e River basin characteristics, impact of human activities and economic analysis required under Article 5, Annex II randr Annex III, and inventory of protected areas required under Article 6, Annex IV of the EU Water Framework Directivee (2000/60/EC) t s Part A – Basin-wide overviewÖ / / Short: “Danube Basin Analysis (WFD Roof Report 2004)” / / d n a l h c s t u e D / / / / The complete report consists of Part A: Basin-wide overview, and Part B: Detailed analysis of the Danube river basin countries 18 March 2005, Reporting deadline: 22 March 2005 Prepared by International Commission for the Protection of the Danube River (ICPDR) in cooperation with the countries of the Danube River Basin District. The Contracting Parties to the Danube River Protection Convention endorsed this report at the 7th Ordinary Meeting of the ICPDR on December 13-14, 2004. The final version of the report was approved 18 March 2005. Overall coordination and editing by Dr. Ursula Schmedtje, Technical Expert for River Basin Management at the ICPDR Secretariat, under the guidance of the River Basin Management Expert Group. ICPDR Document IC/084, 18 March 2005 International Commission for the Protection of the Danube River Vienna International Centre D0412 P.O.
    [Show full text]
  • S E R B I a Knin ˆ Bor
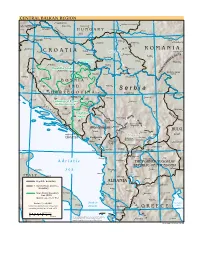
    CENTRAL BALKAN REGION 16 18 20 22 Nagykanizsa Tisza Hódmezövásárhely Dravaˆ Kaposvár Szekszárd SLOVENIA P Celje Varazdin A Szeged N H U N G A R Y N Arad O N Pécs 46 I 46 A Danube Subotica Mures N Bjelovar B A Zagreb S Kikinda Deva I Tisa N Sombor Timisoara¸ Hunedoara T N A Karlovac B A R O M A N I A Sisak C R O A T I A Osijek Vojvodina Petroseni Sava Vukovar Zrenjanin S Resita¸ ¸ LP Novi Sad A ˆ N IA Slavonski Brod Federation of Bosnia Vrsac N and Herzegovina Danube A Tirgu-Jiu V Prijedor Ruma L ˆ ˆ ˆ Y S Bihac Republika Srpska Brcko Pancevo N A D Banja Luka Doboj Sava R Drobeta-Turnu Bijeljina Sabac Belgrade Danube T Severin Udbina I Smederevo Kljuc Tuzla N B O S N I A A A N D Valjevo Danube Zenica Drina R S e r b i a Knin ˆ Bor 44 H E R Z E G O V I N A Srebrenica Kragujevac 44 Glamoc I ˆ Vidin Calafat C Sarajevo Uzice Paracin´ Šibenik Pale Kraljevo Federation of Bosnia ˆ Morava D and Herzegovina Gorazde Split A ˆ L A M Foca Montana A T L Nis´ B I Republika A Mostar L A Priboj K P Srpska A ˆ Ta ra Novi Pazar N M Ploce S Bijelo TS. Piva Polje Neum Kosovska Mitrovica Berane Montenegro BULG. Nikšic´ Pec´ Priština Dubrovnik Kosovo Vranje Pernik CROATIA Podgorica Dakovica Gnjilane NORTH (Djakovica) Uroševac Kotor ALBANIAN Kyustendil ALPS Prizren A Lake I N Kumanovo Scutari N Kukës A 42 Shkodër L Tetovo Skopje 42 Bar P R A S Gostivar Štip Shëngjin Titov Veles A d r i a t i c Peshkopi THE FORMER YUGOSLAV REPUBLIC OF MACEDONIA Vardar Strumica Barletta S e a Tirana Prilep Lake Durrës Ohrid I T A L Y Bari Elbasan Ohrid Bitola Republic boundary
    [Show full text]
  • The Excesively Rainy Summer of 2018 in South-Western Romania in the Context of Climate Changes
    RISCURI ŞI CATASTROFE, NR. XVIII, VOL. 24, NR. 1/2019 THE EXCESIVELY RAINY SUMMER OF 2018 IN SOUTH-WESTERN ROMANIA IN THE CONTEXT OF CLIMATE CHANGES I. MARINICĂ5, ANDREEA MARINICĂ6 Abstract. The summer of 2018 was warm and extremely rainy. The rainy summer feature is due to the first two months of summer in which the monthly average rainfall (calculated for the whole region) was very high. In June the monthly average monthly rainfall was 162.8 l / m2, and its percentage deviation from normal was 93.4% (almost twice the normal) and in July the average monthly quantities for the whole region was 138.0 l / m2 and its percentage deviation from normal 112.4% (more than twice the normal). The average air temperature average was 21.9°C and its deviation from normal 1.2°C, which shows that the summer was warm. The dry and warm weather, usually in summer in Oltenia, started on 2 June, 1818 and extended throughout autumn, seriously affecting the beginning of the 2018-2019 agricultural year by delaying the establishment of autumn crops. Throughout the summer there were 7 overly rainy intervals, which amounted to over 15 days of rain. Due to synoptic situations, usually unusual summer, which caused torrential rains, the summer of 2018 changed the way to achieve seasonal climatic forecasts at three-month intervals at 4-week intervals. This is still a confirmation of the ongoing climate change across the planet, and summer 2018 will remain in the history of the climate as the one that has changed the seasonal weather forecast reference range.
    [Show full text]
  • Study for Evaluating the Water Quality of the Jiu River in Gorj County
    Annals of the „Constantin Brancusi” University of Targu Jiu, Engineering Series , No. 4/2020 STUDY FOR EVALUATING THE WATER QUALITY OF THE JIU RIVER IN GORJ COUNTY DELIA NICA-BADEA*, Constantin Brancusi University Targu – Jiu, Romania ANIELA BALACESCU, Constantin Brancusi University Targu – Jiu, Romania * Corresponding author: [email protected] Abstract: This paper presents a study conducted in the autumn season 2018, whose main objective was to assess the water quality of the Jiu River in the administrative territory of Gorj County. Based on the physico-chemical parameters determined in three sampling points on the direction of river flow, we analyzed the data and established the water quality class from an ecological point of view by reference to elements and physico-chemical quality standards according to O 161/2006. From the perspective of ecological status, most parameters fall into quality class I for all three water segments, except: P-PO4 class IV. The WQI values calculated for each parameters vary depending on the analyzed segment and fall into different quality classes: Excellent (DO, BOD, Nitrate, Phosphates, pH); Good (TDS; BOD –SJ3); Bad (Temperature); Very Bad (Turbidity). The general WQI varies very little, respectively: 79, 78, 77, falling within the Good quality range, decreasing towards the southern segment of the Jiu River. The assessment of the quality of water bodies described in this study, reveals that the Jiu River is a clean body of water, a fact which has also been confirmed by national and European authorities in the periodic in recent reports. Keywords: Jiu River, Water quality parameters, Ecological status, Water Quality Index 1.
    [Show full text]
  • Thermo-Mineral Waters from the Cerna Valley Basin (Romania)
    Studia Universitatis Babeş-Bolyai, Geologia, 2008, 53 (2), 41 – 54 Thermo-mineral waters from the Cerna Valley Basin (Romania) Ioan POVARĂ1*, Georgel SIMION2† & Constantin MARIN1 1„Emil Racoviţă” Institute of Speleology, Frumoasă 31, 78114, Bucharest, Romania 2 S.C. Prospecţiuni SA, Caransebeş 1, 12271, Bucharest, Romania († deceased) Received: May 2008, accepted November 2008 Available online November 2008 ABSTRACT. In the Cerna Valley basin, located southwest of the Southern Carpathians and upstream from the confluence of Cerna with Belareca, an aquifer complex has developed. The basin is strongly influenced by hydrogeothermal phenomena, acting within two major geological structures, the Cerna Syncline and the Cerna Graben. The complex consists mainly of Jurassic and Cretaceous carbonate rocks, as well as the upper part of the Cerna Granite that is highly fractured, tectonically sunken into the graben. The geothermal investigations have shown the existence of some areas with values of the geothermal gradient falling into the 110-200ºC/km interval, and temperatures of 13.8-16ºC at the depth of 30 m. The zone with the maximal flux intensity is situated between the Băile Herculane railway station and the Crucea Ghizelei Well, an area where 24 sources (10 wells and 14 springs) are known. The geothermal anomaly is also extended to the south (Topleţ), north (Mehadia) and NE (Piatra Puşcată), a fact, which is stressed by the existence of hypothermal springs with low mineralization. The physical-chemical parameters of the sources show a strong N-S variability. At the entire thermo-mineral reservoir scale, the temperature of the water sources, the total mineralization, and the H2S quantity are increasing from the north to the south, and the pH and natural radioactivity are following the same trend.
    [Show full text]
  • Romanian Society of Applied Geophysics
    IS CERNA-JIU FAULT (SOUTH CARPATHIANS, ROMANIA) BEING REACTIVATED? BEHAVIOUR PATTERNS RESEMBLING THOSE ENCOUNTERED AT THE WESTERN TERMINATION OF THE NORTH ANATOLIAN FAULT Horia Mitrofan1, Florina Chitea1,2, Mirela-Adriana Anghelache1, Constantin Marin3, Nicoleta Cadicheanu1, Ioan Povară3, Alin Tudorache3, Daniela Elena Ioniţă4 1 “Sabba Ştefănescu” Institute of Geodynamics of the Romanian Academy, Bucharest, Romania 2 Department of Geophysics, Faculty of Geology and Geophysics, University of Bucharest, Romania 3 “Emil Racoviţă” Institute of Speleology of the Romanian Academy, Bucharest, Romania 4 Department of Analytical Chemistry, Faculty of Chemistry, University of Bucharest, Romania Two basement nappe systems (designated as “Lower Danubian” and “Upper Danubian” respectively) occupy the lowermost structural position within the South Carpathians Alpine nappe pile (Iancu et al., 2005). Each of those two Danubian units includes a Neoproterozoic metamorphic rocks basement, overlain by a Mesozoic (Liassic to Late Cretaceous) sedimentary cover. In the SW extremity of the South Carpathians, a major control on the geometry of the contact between the two Danubian nappe systems has been exerted by the Tertiary age Cerna-Jiu strike-slip major fault, for which a dextral average displacement of 35 km was estimated (Berza and Drăgănescu, 1988). Along the Cerna-Jiu fault, the South Carpathians orogen has been completing a clockwise rotation around the Moesian Platform western edge. The last stage of this process has been accompanied (e.g., Linzer et al., 1998) by extensional deformation resulting in the opening, during the Badenian (ca. 15 Ma ago), of several sedimentary basins: Bahna, Orşova, Donji Milanovac, Mehadia, Bozovici, Liubcova. Those pull-apart and transtensional basins became disconnected from each other after the Badenian, then sedimentation progressively ceased – last, during the Early Pannonian (ca.
    [Show full text]
  • Comparative Study of Heavy Metals from Rivers Around Ramnicu Valcea and Craiova Chemical Platforms from Romania
    Asian Journal of Chemistry Vol. 22, No. 4 (2010), 3169-3172 Comparative Study of Heavy Metals from Rivers Around Ramnicu Valcea and Craiova Chemical Platforms from Romania CRISTIAN MLADIN*, ANISOARA PREDA†, IOAN STEFANESCU† and CRISTINA BARBU‡ Mecro System, 100P, Timisoara Blvd., Bucharest-6, RO-061334, Romania E-mail: [email protected] In this paper, the analysis of heavy metals from Olt river around Ramnicu Valcea chemical platform and from Jiu river around Craiova chemical platform during three months before and after industrial zone are presented. Key Words: Heavy metals, Chemical platforms, Industrial zone, Inductively coupled plasma mass spectroscopy. INTRODUCTION In previous years, water quality in Romania has slightly improved only because industry and agricultural water consumption has decreased as a direct result of poor economic conditions and therefore their quantity of wastewater1 discharged into surface waters (lakes, rivers and streams) has decreased. The quality of surface water in Romania is most impacted by its wastewater2. Most of the wastewater requiring treatment and discharged by local utilities is either insufficiently treated or untreated, due to the lack of wastewater treatment capacity and/or its ineffective operation. Olt river flows through Valcea county: The main stationary sources of pollution within this hydrographical basin, area Valcea are the following industries: Oltchim Ramnicu Valcea, Uzinele Sodice Govora through chemical pollution and Ramnicu Valcea communal economy activities. Since 1968, the Oltchim Rm Valcea plant has been an important source for many types of pollutants due to a wide range of produced chemicals, both inorganic and organic substances3. Heavy metals and organic compounds, such as pesticides, HCH, chlorine residues of various types are the main types of pollutant.
    [Show full text]
  • Toponymic Homonymies and Metonymies: Names of Rivers Vs
    ONOMÀSTICA 5 (2019): 91–114 | RECEPCIÓ 21.6.2018 | ACCEPTACIÓ 26.8.2018 Toponymic homonymies and metonymies: names of rivers vs names of settlements Oliviu Felecan & Nicolae Felecan Technical University of Cluj-Napoca North University Centre of Baia Mare (Romania) [email protected] Abstract: This paper analyses several toponymic homonymies and metonymies in Romania. Due to the country’s rich hydrographic network, there are many hydronymic and oikonymic similarities. Most often, the oikonyms borrow the names of rivers which, diachronically, enjoy the status of initial name bearers. However, there are various examples in which oikonyms and hydronyms are not completely homonymous, as numerous compounds or derivatives exist, etymologically and lexicologically eloquent in the contexts described. Keywords: toponymic homonymies and metonymies, hydronyms, oikonyms Homonímies i metonímies toponímiques: noms dels rius vs. noms dels assentaments Resum: Aquest treball analitza diverses homonímies i metonímies existents a la toponímia de Romania. En el context d’un país caracteritzat per la importància de la xarxa hidrogràfica, criden l’atenció les nombroses similituds existents entre els hidrònims i els noms dels assentaments de població. Molt sovint aquests últims, a Romania, prenen en préstec els noms dels rius −els quals, diacrònicament, gaudeixen de la condició de portadors de noms inicials. Tot i això, hi ha diversos exemples en què noms d’assentaments de població i hidrònims no són completament homònims: es tracta, sobretot, de casos de
    [Show full text]