DOCSLIB.ORG

Muon Physics: a Pillar of the Standard Model

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Muon Physics: a Pillar of the Standard Model Typeset with jpsj2.cls <ver.1.2> Full Paper Muon Physics: A Pillar of the Standard Model B. Lee Roberts ∗ Department of Physics Boston University Boston, MA 02215, USA (Received October 5, 2018) Since its discovery in the 1930s, the muon has played an important role in our quest to understand the sub-atomic theory of matter. The muon was the first second-generation standard-model particle to be discovered, and its decay has provided information on the (V ector − Axial V ector) structure of the weak interaction, the strength of the weak in- teraction, GF , and the conservation of lepton number (flavor) in muon decay. The muon’s anomalous magnetic moment has played an important role in restricting theories of physics beyond the standard standard model, where at present there is a 3.4 σ difference between the experiment and standard-model theory. Its capture on the atomic nucleus has provided valu- able information on the modification of the weak current by the strong interaction which is complementary to that obtained from nuclear β decay. KEYWORDS: muon, weak decay, muon capture, magnetic moment, lepton flavor violation 1. Introduction cause of the modification of the Coulomb potential in- The muon was first observed in a Wilson cloud cham- side the nucleus, and these x rays have provided infor- ber by Kunze1 in 1933, where it was reported to be “a mation on nuclear root-mean-square charge radii. The particle of uncertain nature.” In 1936 Anderson and Ned- Lamb shift in muonic hydrogen, ∆E2P −2S , which is being dermeyer2 reported the presence of “particles less mas- measured at at the Paul Scherrer Insitut (PSI), is given 7 2 3 sive than protons but more penetrating than electrons” by 209.974(6) 5.226Rp +0.036Rp meV, where Rp is the proton rms− charge radius. This experiment should in cosmic rays, which was confirmed in 1937 by Street and Stevenson,3 Nishina, Tekeuchi and Ichimiya,4 and provide a precise measurement of Rp. The weak nuclear by Crussard and Leprince-Ringuet.5 The Yukawa theory capture, called ordinary muon capture (OMC), of the muon on the atomic nucleus following the cascade to the of the nuclear force had predicted such a particle, but − 1S ground state, µ +Z Z− + νµ, is the analog this “mesotron” as it was called, interacted too weakly N → 1 N with matter to be the carrier of the strong force. Today to the weak capture of a K-shell electron by the nucleus, we understand that the muon is a second generation lep- and provides information on the modification of the weak ton, with a mass about 207 times the electron’s. Like the interaction by the hadronic matter. The muon mass of 106 MeV restricts the muon to electron, the muon obeys quantum electrodynamics, and ∼ can interact with other particles through the electromag- decay into the electron, neutrinos, and photons. Thus muon decay is a purely leptonic process, and the domi- netic and weak forces. Unlike the electron which appears − − to be stable, the muon decays through the weak force. nant decay mode is µ e + νµ +¯νe. This three-body arXiv:0704.2394v1 [hep-ex] 18 Apr 2007 → The muon lifetime of 2.2 µs permits one to make pre- decay tells us that the individual lepton number, electron cision measurements of its properties, and to use it as a and muon, is conserved separately, and that the two fla- 10 tool to study the semileptonic weak interaction, nuclear vors (kinds) of neutrinos are distinct particles. Here − − + + properties, as well as magnetic properties of condensed the µ and e are “particles” and the µ and e are the matter systems. The high precision to which the muo- antiparticles. In the 1950s, it became possible to make nium (µ+e− atom) hyperfine structure can be measured pions, and thus muons, in the laboratory. The energeti- + and calculated makes it a significant input parameter in cally favorable decay µ eγ was searched for and not 8 → −5 the determination of fundamental constants.6 In this re- found to a relative branching ratio of < 2 10 . Also searched for was the neutrinoless capture of× a µ− on an view, I will focus on the role of the muon in particle − − physics. atomic nucleus, µ + e + , which was not found at the level of 5 N10 →−4. SuchN processes are said to A beam of negative muons can be brought to rest in ∼ × matter, where hydrogen-like atoms are formed, with a “violate lepton flavor,” and continue to be the object of nuclear charge of Z. The Bohr radius for a hydrogen- present and planned studies reaching to sensitivities of −14 −16 like atom is inversely proportional to the orbiting par- 10 and 10 , respectively. 2 2 ticle’s mass (rn = [n ~c]/[mc Zα] ), so that for the The muon, like the electron, is a spin 1/2 lepton, with lowest quantum numbers of high-Z muonic atoms, the a magnetic moment given by muon is well inside of the atomic electron cloud, with q q~ (gs 2) ~µs = gs( )~s; µ = (1+ a) ; a − ; the Bohr radius of the 1S atomic state well inside the 2m 2m ≡ 2 nucleus. The 2P 1S x-ray energies are shifted be- (1) → where the muon charge q = e, and gs, the Land´e g- ± ∗E-mail address: [email protected] 1 2 J. Phys. Soc. Jpn. Full Paper B. Lee Roberts factor is slightly greater than the Dirac value of 2. The middle equation above is useful from a theoretical point of view, as it separates the magnetic moment into two pieces: the Dirac moment which is unity in units of the appropriate magneton, e~/2m, and is predicted by the Dirac equation; and the anomalous (Pauli) moment, (a) (b) (c) where the dimensionless quantity a is referred to as the anomaly. The muon anomaly, like the electron’s, arises Fig. 1. Muon decay in (a) the standard model; (b) the Fermi from radiative corrections that are discussed below. theory; (c) radiative corrections to the Fermi theory. When the muon was discovered, it was an unexpected surprise. Looking at this from our 21st century perspec- 14 tive, it is easy to forget how we reached what is now called electroweak gauge coupling g is related to GF by the “standard model” of subatomic physics, which incor- 2 GF g porates three generations of leptons, e, µ and τ and their = 2 (1 + ∆r) (2) neutrinos; three generations of quarks; the electro-weak √2 8MW gauge bosons, γ W and Z; and the gluons that carry the where ∆r represents the weak boson mediated tree-level strong force. When this author joined the field as a grad- process and its radiative corrections.15 In the standard uate student in the mid 1960s, none of this was clear. model, the Fermi constant is related to the vacuum ex- 2 Quarks were viewed by many as a mathematical device, pectation value of the Higgs field by GF =1/(√2 v ). not as constituent particles. Even after quarks were in- While the Fermi theory is nonrenormalizeable, the ferred from deep inelastic electron scattering off the pro- QED radiative corrections are finite to first order in GF , ton, we only knew of the existence of three of them. While and to all orders in the fine-structure constant α. This 14 the V A structure of the weak interaction was first in- gives the relationship between GF and the muon life- − ferred from nuclear β decay, the study of muon decay has time, τµ, provided a useful laboratory in which to study the purely 1 G2 mµ5 leptonic weak interaction, to search for physics beyond F = 3 (1 + ∆q) (3) the standard model, such as additional terms in the in- τµ 192π teraction besides the standard-model V A structure, as where ∆q is the sum of phase space, and QED and − well as looking for standard model forbidden decays like hadronic radiative corrections. More properly one should µ eγ. For many years, the experimental value of the write G since new physics contributions could make G → µ muon’s anomalous magnetic moment has served to con- different for the three leptons.16 strain physics beyond the standard model, and continues The MuLan experiment at PSI has recently re- that role today. ported a new measurement of the muon lifetime 2.197 013(21)(11) µs ( 11 parts per million (ppm)),17 G 2. Muon Decay and F to be compared with± the previous world average − − 18 The muon decay µ e νµν¯e is purely leptonic. 2.197 03(4) µs (19 ppm). The new world average → Since mµ << MW , muon decay can be described by muon lifetime of 2.197 019(21) µs gives, assuming a local four-fermion (contact) interaction. While non- only standard-model physics in muon decay, GF = renormalizeable, at low energies it provides an excel- 1.166 371(6) 10−5 GeV2 (5 ppm). This experiment × lent approximation to the full electroweak theory. The should eventually reach a precision of 1 ppm on τµ. weak Lagrangian is written as a current-current interac- tion, where the leptonic current is of the (V A) form, 3. Nuclear Muon Capture − uγ¯ λ(1 γ )u. The weak capture of a muon on a proton has much in − 5 Michel11 first wrote down a parameterization of muon common with nuclear β decay. As for other low-energy decay, defining five parameters, ρ, η, ξ, δ and h, which weak processes, the interaction can be described as a are combinations of the different possible couplings al- current-current interaction with the (V A) leptonic cur- λ − lowed by Lorentz invariance in muon decay.
Load more

Recommended publications
  • On the Mass Spectrum of Exotic Protonium Atom in Oscillator Representation Method
    International Journal of Advanced Science and Technology Vol.74 (2015), pp.43-48 http://dx.doi.org/10.14257/ijast.2015.74.05 On the Mass Spectrum of Exotic Protonium Atom in Oscillator Representation Method Arezu Jahanshir Assistant professor and faculty member of Bueinzahra Technical University, Iran [email protected] Abstract In the given paper one determines the constituent mass of the bound state and binding energy of hadronic exotic system, according to the basis investigation of the asymptotically behavior of the loop function of scalar particles in the external electromagnet field are analytically determined exploration of these states through relativistic and non-perturbative corrections. It is shown that, the mass spectrum of a relativistic bound state of protonium consisting from proton and anti-proton is differing from a mass of initial particles. Keywords: protonium, constituent mass, Hamiltonian, Green function, scalar particles 1. Introduction All of theoretical high energy physician by using mathematical methods and new theories try to understand how bound state arise in the formalism of quantum field theory and to work out effective methods to calculate all characteristics of these bound states, especially their masses, binding energy and spin interactions. The analysis of a bound state is difficult when the interaction have to be considered as relativistic, i.e. when they travel at speeds considerably near the "c". The theoretical criterion is that the coupling constant should be strong [1-6] and masses of intermediate particles gluons in quantum chromodynamic should be big in comparison with masses of constituents. New importance to the exotic hadronic bound state physics was given by the development of quantum chromodynamic, the modern theory of strong interactions.
    [Show full text]
  • Progress and Simulations for Intranuclear Neutron-Antineutron 40Ar Transformations in 18 Joshua L
    PHYSICAL REVIEW D 101, 036008 (2020) Progress and simulations for intranuclear neutron-antineutron 40Ar transformations in 18 Joshua L. Barrow * The University of Tennessee at Knoxville, Department of Physics and Astronomy, † 1408 Circle Drive, Knoxville, Tennessee 37996, USA ‡ Elena S. Golubeva and Eduard Paryev§ Institute for Nuclear Research, Russian Academy of Sciences, Prospekt 60-letiya Oktyabrya 7a, Moscow 117312, Russia ∥ Jean-Marc Richard Institut de Physique des 2 Infinis de Lyon, Universit´e de Lyon, CNRS-IN2P3–UCBL, 4 rue Enrico Fermi, Villeurbanne 69622, France (Received 10 June 2019; accepted 29 January 2020; published 18 February 2020) With the imminent construction of the Deep Underground Neutrino Experiment (DUNE) and Hyper- Kamiokande, nucleon decay searches as a means to constrain beyond standard model extensions are once again at the forefront of fundamental physics. Abundant neutrons within these large experimental volumes, along with future high-intensity neutron beams such as the European Spallation Source, offer a powerful, high-precision portal onto this physics through searches for B and B − L violating processes such as neutron-antineutron transformations (n → n¯), a key prediction of compelling theories of baryogenesis. With this in mind, this paper discusses a novel and self-consistent intranuclear simulation of this process 40 within 18Ar, which plays the role of both detector and target within the DUNE’s gigantic liquid argon time projection chambers. An accurate and independent simulation of the resulting intranuclear annihilation respecting important physical correlations and cascade dynamics for this large nucleus is necessary to understand the viability of such rare searches when contrasted against background sources such as atmospheric neutrinos.
    [Show full text]
  • Exotic Double-Charm Molecular States with Hidden Or Open Strangeness and Around 4.5 ∼ 4.7 Gev
    PHYSICAL REVIEW D 102, 094006 (2020) Exotic double-charm molecular states with hidden or open strangeness and around 4.5 ∼ 4.7 GeV † Fu-Lai Wang and Xiang Liu * School of Physical Science and Technology, Lanzhou University, Lanzhou 730000, China and Research Center for Hadron and CSR Physics, Lanzhou University and Institute of Modern Physics of CAS, Lanzhou 730000, China (Received 1 September 2020; accepted 16 October 2020; published 10 November 2020) à In this work, we investigate the interactions between the charmed-strange meson (Ds;Ds )inH-doublet à and the (anti-)charmed-strange meson (Ds1;Ds2)inT-doublet, where the one boson exchange model is adopted by considering the S-D wave mixing and the coupled-channel effects. By extracting the effective ¯ potentials for the discussed HsTs and HsTs systems, we try to find the bound state solutions for the corresponding systems. We predict the possible hidden-charm hadronic molecular states with hidden à ¯ PC 0−− 0−þ à ¯ à strangeness, i.e., the Ds Ds1 þ c:c: states with J ¼ ; and the Ds Ds2 þ c:c: states with PC −− −þ J ¼ 1 ; 1 . Applying the same theoretical framework, we also discuss the HsTs systems. Unfortunately, the existence of the open-charm and open-strange molecular states corresponding to the HsTs systems can be excluded. DOI: 10.1103/PhysRevD.102.094006 ¯ ðÞ I. INTRODUCTION strong evidence to support these Pc states as the ΣcD - – Studying exotic hadronic states, which are very type hidden-charm pentaquark molecules [10 16]. different from conventional mesons and baryons, is an Before presenting our motivation, we first need to give a intriguing research frontier full of opportunities and chal- brief review of how these observed XYZ states were lenges in hadron physics.
    [Show full text]
  • Antiproton–Proton Scattering Experiments with Polarization ( Collaboration) PAX Abstract
    Technical Proposal for Antiproton–Proton Scattering Experiments with Polarization ( Collaboration) PAX arXiv:hep-ex/0505054v1 17 May 2005 J¨ulich, May 2005 2 Technical Proposal for PAX Frontmatter 3 Technical Proposal for Antiproton–Proton Scattering Experiments with Polarization ( Collaboration) PAX Abstract Polarized antiprotons, produced by spin filtering with an internal polarized gas target, provide access to a wealth of single– and double–spin observables, thereby opening a new window to physics uniquely accessible at the HESR. This includes a first measurement of the transversity distribution of the valence quarks in the proton, a test of the predicted opposite sign of the Sivers–function, related to the quark dis- tribution inside a transversely polarized nucleon, in Drell–Yan (DY) as compared to semi–inclusive DIS, and a first measurement of the moduli and the relative phase of the time–like electric and magnetic form factors GE,M of the proton. In polarized and unpolarized pp¯ elastic scattering, open questions like the contribution from the odd charge–symmetry Landshoff–mechanism at large t and spin–effects in the extraction | | of the forward scattering amplitude at low t can be addressed. The proposed de- | | tector consists of a large–angle apparatus optimized for the detection of DY electron pairs and a forward dipole spectrometer with excellent particle identification. The design and performance of the new components, required for the polarized antiproton program, are outlined. A low–energy Antiproton Polarizer Ring (APR) yields an antiproton beam polarization of Pp¯ = 0.3 to 0.4 after about two beam life times, which is of the order of 5–10 h.
    [Show full text]
  • Plasma Physics and Fusion Research Royal Institute of Technology S-100 44 Stockholm Sweden Trita-Pfu-91-05
    ISSN 0348-7644 TRITA-PFU-91-05 NEUTRON TIME-OF-FLIGHT COUNTERS AND SPECTROMETERS FOR DIAGNOSTICS OF BURNING FUSION PLASMAS T. Elevant and M. Olsson Research and Training Programme on CONTROLLED THERMONUCLEAR FUSION AND PLASMA PHYSICS (EUR-NFR) PLASMA PHYSICS AND FUSION RESEARCH ROYAL INSTITUTE OF TECHNOLOGY S-100 44 STOCKHOLM SWEDEN TRITA-PFU-91-05 NEUTRON TIME-OF-FLIGHT COUNTERS AND SPECTROMETERS FOR DIAGNOSTICS OF BURNING FUSION PLASMAS T. Elevant and M. Olsson Stockholm, February 1991 Department of Plasma Physics and Fusion Research Royal Institute of Technology 5-100 44 Stockholm, Sweden Neutron Time-of-Flight Counters and Spectrometers for Diagnostics of burning Fusion Plasmas. T. Elevant and M. Olsson. Department of Plasma Physics and Fusion Research, The Royal Institute of Technology, S-10044 Stockholm, Sweden. ABSTRACT Experiment with burning fusion plasmas in tokamaks will place particular requirements on neutron measurements from radiation resistance-, physics-, burn control- and reliability considerations. The possibility to meet these needs by measurements of neutron fluxes and energy spectra by means of time-of-flight techniques are described. Reference counters and spectrometers are proposed and characterized with respect to efficiency, count-rate capabilities, energy resolution and tolerable neutron and y-radiation background levels. The instruments can be used in a neutron camera and are capable to operate in collimated neutron fluxes up to levels corresponding to full nuclear output power in the next generation of experiments. Energy resolutions of the spectrometers enables determination of ion temperatures from 3 [keV] through analysis of the Doppler broadening. Primarily, the instruments are aimed for studies of 14 [MeV] neutrons produced in [d,t]-plasmas but can, after minor modifications, be used for analysis of 2.45 [McV] neutrons produced in [d,d]-plasmas.
    [Show full text]
  • Printed Here
    PHYSICAL REVIEW C, VOLUME 66, NUMBER 3 Selected Abstracts from Other Physical Review Journals Abstracts of papers which are published in other Physical Review journals and may be of interest to Physical Review C readers are printed here. The Editors of Physical Review C routinely scan the abstracts of Physical Review D papers. Appropriate abstracts of papers in other Physical Review journals may be included upon request. Supernova neutrinos and the LSND evidence for neutrino oscil- We present a study of inhomogeneous big bang nucleosynthesis lations. Michel Sorel and Janet Conrad, Department of Physics, with emphasis on transport phenomena. We combine a hydrody- Columbia University, New York, New York 10027. ͑Received 15 namic treatment to a nuclear reaction network and compute the light December 2001; published 23 August 2002͒ element abundances for a range of inhomogeneity parameters. We ®nd that shortly after annihilation of electron-positron pairs, Thom- Å The observation of the ␯e energy spectrum from a supernova son scattering on background photons prevents the diffusion of the burst can provide constraints on neutrino oscillations. We derive remaining electrons. Protons and multiply charged ions then tend to formulas for adiabatic oscillations of supernova antineutrinos for a diffuse into opposite directions so that no net charge is carried. Ions variety of 3- and 4-neutrino mixing schemes and mass hierarchies with ZϾ1 get enriched in the overdense regions, while protons which are consistent with the Liquid Scintillation Neutrino Detector diffuse out into regions of lower density. This leads to a second Å →Å ͑LSND͒ evidence for ␯␮ ␯e oscillations. Finally, we explore the burst of nucleosynthesis in the overdense regions at TϽ20 keV, constraints on these models and LSND given by the supernova SN leading to enhanced destruction of deuterium and lithium.
    [Show full text]
  • Relativistic Kinematics of Particle Interactions Introduction
    le kin rel.tex Relativistic Kinematics of Particle Interactions byW von Schlipp e, March2002 1. Notation; 4-vectors, covariant and contravariant comp onents, metric tensor, invariants. 2. Lorentz transformation; frequently used reference frames: Lab frame, centre-of-mass frame; Minkowski metric, rapidity. 3. Two-b o dy decays. 4. Three-b o dy decays. 5. Particle collisions. 6. Elastic collisions. 7. Inelastic collisions: quasi-elastic collisions, particle creation. 8. Deep inelastic scattering. 9. Phase space integrals. Intro duction These notes are intended to provide a summary of the essentials of relativistic kinematics of particle reactions. A basic familiarity with the sp ecial theory of relativity is assumed. Most derivations are omitted: it is assumed that the interested reader will b e able to verify the results, which usually requires no more than elementary algebra. Only the phase space calculations are done in some detail since we recognise that they are frequently a bit of a struggle. For a deep er study of this sub ject the reader should consult the monograph on particle kinematics byByckling and Ka jantie. Section 1 sets the scene with an intro duction of the notation used here. Although other notations and conventions are used elsewhere, I present only one version which I b elieveto b e the one most frequently encountered in the literature on particle physics, notably in such widely used textb o oks as Relativistic Quantum Mechanics by Bjorken and Drell and in the b o oks listed in the bibliography. This is followed in section 2 by a brief discussion of the Lorentz transformation.
    [Show full text]
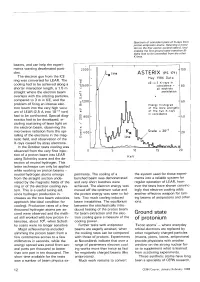
  • Ground State of Protonium
    Spectrum of coincident pairs of X-rays from proton-antiproton atoms. Selecting a transi­ tion to the first atomic excited state (L line) enables the first ground state transition (K- alpha line) to be unravelled from the other K lines. beams, and can help the experi­ ments wanting decelerated parti­ cles. The electron gun from the ICE ring was converted for LEAR. The cooling had to be achieved along a shorter interaction length, a 1.5 m straight where the electron beam overlaps with the orbiting particles, compared to 3 m in ICE, and the problem of firing an intense elec­ tron beam into the very high vacu­ um of LEAR (2.5 A into 10"11 torr) had to be confronted. Special diag­ nostics had to be developed, in­ cluding scattering of laser light on the electron beam, observing the microwave radiation from the spi­ ralling of the electrons in the mag­ netic field, and observation of the X-rays caused by stray electrons. In the October tests cooling was observed from the very first injec­ tion of a proton beam into LEAR using Schottky scans and the de­ tection of neutral hydrogen. This latter technique can only be applied while working on proton beams - neutral hydrogen atoms emerge periments. The cooling of a the system used for these experi­ from the straight section unde- bunched beam was demonstrated ments into a reliable system for viated by the magnetic fields of the and very short bunches were regular operation of LEAR, how­ ring or of the electron cooling sys­ achieved.
    [Show full text]
  • Compact Dark Matter Objects Via $ N $ Dark Sectors
    Compact Dark Matter Objects via N Dark Sectors Gia Dvali,1, 2 Emmanouil Koutsangelas,1, 2, ∗ and Florian K¨uhnel3 1 Arnold Sommerfeld Center, Ludwig-Maximilians-Universit¨at,Theresienstraße 37, 80333 M¨unchen,Germany, 2 Max-Planck-Institut f¨urPhysik, F¨ohringerRing 6, 80805 M¨unchen,Germany 3 The Oskar Klein Centre for Cosmoparticle Physics, Department of Physics, Stockholm University, AlbaNova University Center, Roslagstullsbacken 21, SE-10691 Stockholm, Sweden (Dated: Monday 27th April, 2020, 12:34am) We propose a novel class of compact dark matter objects in theories where the dark matter consists of multiple sectors. We call these objects N-MACHOs. In such theories neither the existence of dark matter species nor their extremely weak coupling to the observable sector represent additional hypotheses but instead are imposed by the solution to the Hierarchy Problem and unitarity. The crucial point is that particles from the same sector have non-trivial interactions but interact only gravitationally otherwise. As a consequence, the pressure that counteracts the gravitational collapse is reduced while the gravitational force remains the same. This results in collapsed structures much lighter and smaller as compared to the ordinary single-sector case. We apply this phenomenon to a dark matter theory that consists of N dilute copies of the Standard Model. The solutions do not rely on an exotic stabilization mechanism, but rather use the same well-understood properties as known stellar structures. This framework also gives rise to new microscopic superheavy structures, for example with mass 108 g and size 10−13 cm. By confronting the resulting objects with observational constraints, we find that, due to a huge suppression factor entering the mass spectrum, these objects evade the strongest constrained region of the parameter space.
    [Show full text]
  • Lawrence Berkeley National Laboratory Recent Work
    Lawrence Berkeley National Laboratory Recent Work Title PROTON-AMTIPROTON ANNIHILATION IN PROTONIUM Permalink https://escholarship.org/uc/item/7br7d1gt Author Desai, Bipin R. Publication Date 1960-01-05 eScholarship.org Powered by the California Digital Library University of California UCRL —9°J4 Cy .2 UNIVERSITY OF CALIFORNIA ernest:' oj:auirence Ddü2vion TWO-WEEK LOAN COPY This is a library Circulating Copy which may be borrowed for two weeks. For a personal retention copy, call Tech. Info. Division, Ext. 5545 4 BERKELEY, CALIFORNIA DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California. - 2 I. 41LL , UCRL-9014 UNIVERSITY OF CALIFORNIA Lawrence Radiation Laboratory Berkeley, California Contract No. W-7405-eng-48 PROTON-ANTIPROTON ANNIHILATION IN PROTONIUM Bipin R.
    [Show full text]
  • Measurement of Strange Baryon–Antibaryon Interactions with Femtoscopic Correlations
    Lawrence Berkeley National Laboratory Recent Work Title Measurement of strange baryon–antibaryon interactions with femtoscopic correlations Permalink https://escholarship.org/uc/item/9m53h9jm Authors Acharya, S Adamová, D Adhya, SP et al. Publication Date 2020-03-10 DOI 10.1016/j.physletb.2020.135223 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Physics Letters B 802 (2020) 135223 Contents lists available at ScienceDirect Physics Letters B www.elsevier.com/locate/physletb Measurement of strange baryon–antibaryon interactions with femtoscopic correlations .ALICE Collaboration a r t i c l e i n f o a b s t r a c t Article history: √Two-particle correlation√ functions were measured for pp, p, p, and pairs in Pb–Pb collisions at Received 25 September 2019 sNN = 2.76 TeV and sNN = 5.02 TeV recorded by the ALICE detector. From a simultaneous fit to all Received in revised form 10 January 2020 obtained correlation functions, real and imaginary components of the scattering lengths, as well as the Accepted 13 January 2020 effective ranges, were extracted for combined p and p pairs and, for the first time, for pairs. Available online 16 January 2020 Effective averaged scattering parameters for heavier baryon–antibaryon pairs, not measured directly, are Editor: L. Rolandi also provided. The results reveal similarly strong interaction between measured baryon–antibaryon pairs, ∗ suggesting that they all annihilate in the same manner at the same pair relative momentum k . Moreover, the reported significant non-zero imaginary part and negative real part of the scattering length provide motivation for future baryon–antibaryon bound state searches.
    [Show full text]
  • Electromagnetic and Spin Properties of Hyperons
    Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1939 Electromagnetic and Spin Properties of Hyperons ELISABETTA PEROTTI ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6214 ISBN 978-91-513-0956-9 UPPSALA urn:nbn:se:uu:diva-406648 2020 Dissertation presented at Uppsala University to be publicly examined in Häggsalen, Ångströmlaboratoriet, Lägerhyddsvägen 1, Uppsala, Friday, 12 June 2020 at 13:00 for the degree of Doctor of Philosophy. The examination will be conducted in English. Faculty examiner: Dr. Luis Alvarez Ruso (Department of Theoretical Physics, Facultad de Ciencias Físicas, Universidad de Valencia). Abstract Perotti, E. 2020. Electromagnetic and Spin Properties of Hyperons. Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1939. 69 pp. Uppsala: Acta Universitatis Upsaliensis. ISBN 978-91-513-0956-9. The study of hyperons improves our understanding of nature in multiple ways. The intrinsic properties of hadrons are not fully understood at a fundamental level. Hence, the electromag- netic properties of hyperons provide complementary information to that of the nucleon and therefore allow for a broader investigation of the structure of matter. Electromagnetic form fac- tors have been extensively studied for the nucleon, and are now addressed also in the hyperon sector. In this thesis, the electromagnetic Σ-Λ hyperon transition form factors have been de- termined at low energies, in a pioneering framework that makes use of dispersion relations to combine theoretical and experimental input. Subsequently this analysis has been extended to the decuplet spin-3/2 Σ -Λ transition. Assuming that these transition form factors are saturated by a two-pion inelasticity, their imaginary part can be written in terms of the pion vector form factor and a pion-hyperon scattering amplitude.
    [Show full text]