DOCSLIB.ORG

ISPRS Abstract Book.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ISPRS Abstract Book.Pdf ISPRS Working Group IV/7 Extraterrestrial Mapping Advances in Planetary Mapping 2007 Lunar and Planetary Institute, Houston, Tx, March 17, 2007 08:30 Registration 09:00 Welcome / Logistics Oral Presentations Moon Chair persons: J. Oberst and J. Haruyama 09:05 – 09:20 Report on the final completion of the unified Lunar control network 2005 and Lunar topographic model B.A. Archinal, M.R. Rosiek, R.L. Kirk, T.L. Hare, and B.L. Reddin 09:20 – 09:35 Global mapping of the Moon with the Lunar Imager/Spectrometer on SELENE J. Haruyama, M. Ohtake, T. Matunaga, T. Morota, C. Honda, M. Torii, Y. Yokota, H. Kawasaki, and LISM working group 09:35 – 09:50 Lunar orbiter laser altimeter on Lunar Reconnaissance Orbiter G. A. Neumann, D. E. Smith, and M. T. Zuber 09:50 – 10:05 LROC – Lunar Reconnaissance Orbiter Camera M.S. Robinson, E.M. Eliason, H.Hiesinger, B.L. Jolliff, A.S. McEwen, M.C. Malin, M.A. Ravine, D. Roberts, P.C. Thomas, and E.P. Turtle Coffee and Poster Viewing Methods in Planetary Mapping Chair persons: J. Haruyama and J. Oberst 10:35 – 10:50 Toward machine geomorphic mapping of planetary surfaces T.F. Stepinski 10:50 – 11:05 MR PRISM - an Image analysis tool and GIS for CRISM A.J. Brown, J. L. Bishop, and M.C. Storrie-Lombardi 11:05 – 11:20 Description of the JPL planetary web mapping server L. Plesea, T.M. Hare, E. Dobinson, and D. Curkendall 11:20 – 11:35 Do we really need to put stereo cameras on landers? A.C. Cook 11:35 – 11:50 Restoration of degraded planetary imagery R. Schmidt, G. Neukum, and the HRSC Co-Investigator Team 11:50 – 12:05 Applying the constant-scale natural boundary mapping technique P.E. Clark, C.S. Clark, and P.D. Lowman 12:05 – 12:10 World maps with Constant-Scale Natural Boundaries: CSNB 2007 (poster introduction) C. S. Clark 12:10 – 12:15 A prototype of Online Conference system for collaborative mapping (poster introduction) Works H. Demura, M. Kanzawa, N. Hirata, and N. Asada Lunch Break and Poster Viewing Mars Chair persons: T. Roatsch and P. Schenk 13:15 – 13:30 The HRSC DTM test C. Heipke, J. Oberst, J. Albertz, M. Attwenger, P. Dorninger, E. Dorrer, M. Ewe, S. Gehrke, K. Gwinner, H. Hirschmüller, J.R.Kim, R.L.Kirk, H. Mayer, J.-P. Muller, R. Rengarajan, M.Rentsch, R. Schmidt, F. Scholten, J. Shan, M. Spiegel, M. Wählisch, G. Neukum, and the HRSC Co-Investigator Team 13:30 – 13:45 Global Mapping of Mars by Systematic Derivation of Mars Express HRSC High-Resolution Digital Elevation Models and Orthoimages K. Gwinner, F. Scholten, R. Jaumann, T. Roatsch, J. Oberst, and G. Neukum 13:45 – 14:00 Simultaneous adjustment of interior and exterior orientation of HRSC on MARS EXPRESS M. Spiegel and G. Neukum 14:00 – 14:15 HRSC Data Proccessing by Matching in Object Space, II. Effects of Image and DTM Filtering S. Gehrke and C. Bischoff 14:15 – 14:30 Where is Viking Lander 2? Recovered Landing Site in MRO Images Not in Agreement with Earlier Predictions J. Oberst, M. Wählisch, and K.-D. Matz 14:30 – 14:45 A new astrometric measurement technique for Phobos using background stars and surface control points K. Willner, J. Oberst, K-D. Matz, T. Roatsch, and H. Hoffmann Coffee Break and Poster Viewing Asteroids Chair persons: P. Schenk and T. Roatsch 15:15 – 15:30 Mapping small bodies with stereophotoclinometry R. W. Gaskell 15:30 – 15:45 Integrated tool for analysis of irregular shaped small bodies N. Hirata, Y. Fujii, H. Demura, and N. Asada 15:45 – 16:00 Global mapping of asteroid CERES with HST/ACS J.-Y. Li, L. A. McFadden, J. Wm. Parker, E. F. Young, and P. C. Thomas Outer Planet Satellites 16:00 – 16:15 Global geologic mapping of Io: data and techniques D. A. Williams, L. P. Keszthelyi, P. E. Geissler, W. L. Jaeger, T. L. Becker, D. A. Crown, P. M. Schenk, and J. A. Rathbun 16.15 – 16:30 Combining Galileo SSI, NIMS, and PPR DATA into GIS to study volcanic centers on Io J.A. Rathbun and S. E. Barrett 16:30 – 16:45 Resolution effects in radarclinometry R. L. Kirk and J. Radebaugh 16:45 – 17:00 High resolution Enceladus atlas derived from CASSINI-ISS images T. Roatsch, M. Wählisch, B. Giese, A. Hoffmeister, A. Kuhn, F. Scholten, K.- D. Matz, G. Neukum, P. Helfenstein, and C. Porco 17:00 Adjourn Posters First stereoscopic RADAR images of Titan R.L. Kirk, E. Howington-Kraus, K.L. Mitchell, S. Hensley, B.W. Stiles, and the Cassini RADAR Team Ultrahigh resolution topografic mapping of Mars with HiRISE stereo images: methods and first results R.L. Kirk, E. Howington-Kraus, M.R. Rosiek, D. Cook, J. Anderson, K. Becker, B.A. Archinal, L. Keszthelyi, R. King, A.S. McEwen, and the HiRISE Team The evolution of Ares Vallis A. Pacifici, G.G. Ori, G. Komatsu, and M. Pondrelli CASSINI-VIMS multiwavelength mapping of Titan J.W. Barnes, J. Ivens, and R.H. Brown Venus on two world maps with constant-scale natural boundaries B.S. Clark and P.E. Clark HRSC data processing by matching in object space, I. joint derivation of DTM and orthoimage S. Gehrke and I. Haase Combining HRSC imagery and MOLA DTM: the first north-polar sheets of the "Topographic image map Mars 1:200,000" S. Gehrke, D. Bornemann, M. Wählisch, and J. Albertz Geological map of the Holden and Eberswalde craters area M. Pondrelli, A.P. Rossi, L. Marinangeli, E. Hauber, G.G. Ori, and G. Neukum Calibration of MOLA pulse spread for interpretation of surface roughness P. Saiger, J. Oberst, and M. Wählisch World maps with Constant-Scale Natural Boundaries: CSNB 2007 C.S. Clark A prototype of Online Conference system for collaborative mapping Works H. Demura, M. Kanzawa, N. Hirata, and N. Asada Report on the final completion of the unified Lunar control network 2005 and Lunar topographic model B.A. Archinal, M.R. Rosiek, R.L. Kirk, T.L. Hare, and B.L. Redding Asteroids and Map Projections: Choices and Compromises P.J. Stooke REPORT ON THE FINAL COMPLETION OF THE UNIFIED LUNAR CONTROL NETWORK 2005 AND LUNAR TOPOGRAPHIC MODEL. B. A. Archinal, M. R. Rosiek, R. L. Kirk, T. L. Hare, and B. L. Redding, U. S. Geological Survey, Astrogeology Team, 2255 N. Gemini Drive, Flagstaff, AZ 86001, USA, [email protected]. Introduction: In order to highlight this project to the average. When the ULCN 2005 solution radii of all 272,931 extraterrestrial mapping community, we repeat here our ear- control points are compared to the a priori radii derived from lier abstract [1], with a corrected Figure 2. A report describ- an interpolation of a combination of Clementine LIDAR and ing the Unified Lunar Control Network 2005 and the files polar Clementine stereo data [6], the differences are not sig- associated with that network is now available as an on-line nificant so the radii must therefore be of similar accuracy. USGS Open-File Report [2] at the location The mean absolute difference of the solution radii from their http://pubs.usgs.gov/of/2006/1367/. A “Readme” file de- a priori values is 137 m, with a standard deviation of 219 m. scribes the available files, including the report text, the Uses of the ULCN 2005: The original reason for doing a original photogrammetric solution input and output files, solution that combined the ULCN (1994) and CLCN was derived files such as information on all the control point primarily to remove the large horizontal errors known to be positions, the expected vertical precision (EVP) of the points present in the CLCN, and thus allow for the possible option and the solution residuals, and a directory containing global of generating an improved Clementine Basemap Mosaic DEMs derived from the point positions. While a paper pro- (CBM)[8] and other Clementine mosaics[9,10]. Indeed, that viding further details about the solution is in preparation, we option still exists, although we have been unable to obtain provide some useful additional information about the solu- funding to carry it out. However, as part of a funded PG&G tion and possible uses for it here. task to generate an initial Lunar GIS, we are creating an The Solution: The ULCN 2005 includes the determina- improved version of the CBM by warping the mosaic based tion of the 3-D positions of 272,931 points on the lunar sur- on the change in point coordinates from the CLCN to the face and the correction of the camera angles for 43,866 ULCN 2005. We are excited to report initial tests show Clementine images, using 546,126 tie point measurements. better results than we hoped for. We tested 3, 6, and 12 pa- The solution RMS is 20 µm (= 0.9 pixels) in the image rameter polynomial warps and have settled on a 6 parameter plane, with the largest residual of 6.4 pixels. The 7 iteration warp. Using a 30°x30° test area and more that 7400 vectors, solution took ~40 hours for completion on a ~2 GHz system. we successfully obtained RMS errors of <110 meters. But There is an average of 46 km2/point and therefore ~6.8 km more importantly, a visual inspection of the registration is between points. This photogrammetric network solution is also impressive (Figure 2 – corrected from reference [1]). the largest planetary control network ever completed. Other We will continue to use 30°x30° tiles for entire global data- details of the solution are given in Table 1.
Load more

Recommended publications
  • Planetary Geologic Mappers Annual Meeting
    Program Lunar and Planetary Institute 3600 Bay Area Boulevard Houston TX 77058-1113 Planetary Geologic Mappers Annual Meeting June 12–14, 2018 • Knoxville, Tennessee Institutional Support Lunar and Planetary Institute Universities Space Research Association Convener Devon Burr Earth and Planetary Sciences Department, University of Tennessee Knoxville Science Organizing Committee David Williams, Chair Arizona State University Devon Burr Earth and Planetary Sciences Department, University of Tennessee Knoxville Robert Jacobsen Earth and Planetary Sciences Department, University of Tennessee Knoxville Bradley Thomson Earth and Planetary Sciences Department, University of Tennessee Knoxville Abstracts for this meeting are available via the meeting website at https://www.hou.usra.edu/meetings/pgm2018/ Abstracts can be cited as Author A. B. and Author C. D. (2018) Title of abstract. In Planetary Geologic Mappers Annual Meeting, Abstract #XXXX. LPI Contribution No. 2066, Lunar and Planetary Institute, Houston. Guide to Sessions Tuesday, June 12, 2018 9:00 a.m. Strong Hall Meeting Room Introduction and Mercury and Venus Maps 1:00 p.m. Strong Hall Meeting Room Mars Maps 5:30 p.m. Strong Hall Poster Area Poster Session: 2018 Planetary Geologic Mappers Meeting Wednesday, June 13, 2018 8:30 a.m. Strong Hall Meeting Room GIS and Planetary Mapping Techniques and Lunar Maps 1:15 p.m. Strong Hall Meeting Room Asteroid, Dwarf Planet, and Outer Planet Satellite Maps Thursday, June 14, 2018 8:30 a.m. Strong Hall Optional Field Trip to Appalachian Mountains Program Tuesday, June 12, 2018 INTRODUCTION AND MERCURY AND VENUS MAPS 9:00 a.m. Strong Hall Meeting Room Chairs: David Williams Devon Burr 9:00 a.m.
    [Show full text]
  • Thermal Studies of Martian Channels and Valleys Using Termoskan Data
    JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 99, NO. El, PAGES 1983-1996, JANUARY 25, 1994 Thermal studiesof Martian channelsand valleys using Termoskan data BruceH. Betts andBruce C. Murray Divisionof Geologicaland PlanetarySciences, California Institute of Technology,Pasadena The Tennoskaninstrument on boardthe Phobos '88 spacecraftacquired the highestspatial resolution thermal infraredemission data ever obtained for Mars. Included in thethermal images are 2 km/pixel,midday observations of severalmajor channel and valley systems including significant portions of Shalbatana,Ravi, A1-Qahira,and Ma'adimValles, the channelconnecting Vailes Marineris with HydraotesChaos, and channelmaterial in Eos Chasma.Tennoskan also observed small portions of thesouthern beginnings of Simud,Tiu, andAres Vailes and somechannel material in GangisChasma. Simultaneousbroadband visible reflectance data were obtainedfor all but Ma'adimVallis. We find thatmost of the channelsand valleys have higher thermal inertias than their surroundings,consistent with previousthermal studies. We show for the first time that the thermal inertia boundariesclosely match flat channelfloor boundaries.Also, butteswithin channelshave inertiassimilar to the plainssurrounding the channels,suggesting the buttesare remnants of a contiguousplains surface. Lower bounds ontypical channel thermal inertias range from 8.4 to 12.5(10 -3 cal cm-2 s-1/2 K-I) (352to 523 in SI unitsof J m-2 s-l/2K-l). Lowerbounds on inertia differences with the surrounding heavily cratered plains range from 1.1 to 3.5 (46 to 147 sr). Atmosphericand geometriceffects are not sufficientto causethe observedchannel inertia enhancements.We favornonaeolian explanations of the overall channel inertia enhancements based primarily upon the channelfloors' thermal homogeneity and the strongcorrelation of thermalboundaries with floor boundaries. However,localized, dark regions within some channels are likely aeolian in natureas reported previously.
    [Show full text]
  • Io in the Near Infrared: Near-Infrared Mapping Spectrometer (NIMS) Results from the Galileo Tlybys in 1999 and 2000 Rosaly M
    JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 106, NO. El2, PAGES 33,053-33,078, DECEMBER 25, 2001 Io in the near infrared: Near-Infrared Mapping Spectrometer (NIMS) results from the Galileo tlybys in 1999 and 2000 Rosaly M. C. Lopes,• L. W. Kamp,• S. Dout6,2 W. D. Smythe,• R. W. Carlson,• A. S. McEwen, 3 P. E. Geissler,3 S. W. Kieffer, 4 F. E. Leader, s A. G. Davies, • E. Barbinis,• R. Mehlman,s M. Segura,• J. Shirley,• and L. A. Soderblom6 Abstract. Galileo'sNear-Infrared Mapping Spectrometer(NIMS) observedIo duringthe spacecraft'sthree flybysin October 1999, November 1999, and February 2000. The observations,which are summarizedhere, were used to map the detailed thermal structure of activevolcanic regions and the surfacedistribution of SO2 and to investigatethe origin of a yet unidentified compoundshowing an absorptionfeature at ---1 •m. We present a summaryof the observationsand results,focusing on the distributionof thermal emission and of SO2 deposits.We find high eruption temperatures,consistent with ultramafic volcanism,at Pele. Such temperaturesmay be present at other hot spots,but the hottest areas may be too small for those temperaturesto be detected at the spatial resolutionof our observations.Loki is the site of frequent eruptions,and the low thermal emissionmay representlavas cooling on the caldera'ssurface or the coolingcrust of a lava lake. High- resolutionspectral observations of Emakong caldera show thermal emissionand SO2 within the same pixels,implying that patchesof SO2 frost and patchesof coolinglavas or sulfur flows are presentwithin a few kilometersfrom one another. Thermal maps of Prometheusand Amirani showthat these two hot spotsare characterizedby long lava flows.The thermal profilesof flows at both locationsare consistentwith insulatedflows, with the Amirani flow field havingmore breakoutsof fresh lava along its length.
    [Show full text]
  • Interpretations of Gravity Anomalies at Olympus Mons, Mars: Intrusions, Impact Basins, and Troughs
    Lunar and Planetary Science XXXIII (2002) 2024.pdf INTERPRETATIONS OF GRAVITY ANOMALIES AT OLYMPUS MONS, MARS: INTRUSIONS, IMPACT BASINS, AND TROUGHS. P. J. McGovern, Lunar and Planetary Institute, Houston TX 77058-1113, USA, ([email protected]). Summary. New high-resolution gravity and topography We model the response of the lithosphere to topographic loads data from the Mars Global Surveyor (MGS) mission allow a re- via a thin spherical-shell flexure formulation [9, 12], obtain- ¡g examination of compensation and subsurface structure models ing a model Bouguer gravity anomaly ( bÑ ). The resid- ¡g ¡g ¡g bÓ bÑ in the vicinity of Olympus Mons. ual Bouguer anomaly bÖ (equal to - ) can be Introduction. Olympus Mons is a shield volcano of enor- mapped to topographic relief on a subsurface density interface, using a downward-continuation filter [11]. To account for the mous height (> 20 km) and lateral extent (600-800 km), lo- cated northwest of the Tharsis rise. A scarp with height up presence of a buried basin, we expand the topography of a hole Ö h h ¼ ¼ to 10 km defines the base of the edifice. Lobes of material with radius and depth into spherical harmonics iÐÑ up h with blocky to lineated morphology surround the edifice [1-2]. to degree and order 60. We treat iÐÑ as the initial surface re- Such deposits, known as the Olympus Mons aureole deposits lief, which is compensated by initial relief on the crust mantle =´ µh c Ñ c (hereinafter abbreviated as OMAD), are of greatest extent to boundary of magnitude iÐÑ . These interfaces the north and west of the edifice.
    [Show full text]
  • Evidence for Volcanism in and Near the Chaotic Terrains East of Valles Marineris, Mars
    43rd Lunar and Planetary Science Conference (2012) 1057.pdf EVIDENCE FOR VOLCANISM IN AND NEAR THE CHAOTIC TERRAINS EAST OF VALLES MARINERIS, MARS. Tanya N. Harrison, Malin Space Science Systems ([email protected]; P.O. Box 910148, San Diego, CA 92191). Introduction: Martian chaotic terrain was first de- ple chaotic regions are visible in CTX images (Figs. scribed by [1] from Mariner 6 and 7 data as a “rough, 1,2). These fractures have widened since the formation irregular complex of short ridges, knobs, and irregular- of the flows. The flows overtop and/or bank up upon ly shaped troughs and depressions,” attributing this pre-existing topography such as crater ejecta blankets morphology to subsidence and suggesting volcanism (Fig. 2c). Flows are also observed originating from as a possible cause. McCauley et al. [2], who were the fractures within some craters in the vicinity of the cha- first to note the presence of large outflow channels that os regions. Potential lava flows are observed on a por- appeared to originate from the chaotic terrains in Mar- tion of the floor as Hydaspis Chaos, possibly associat- iner 9 data, proposed localized geothermal melting ed with fissures on the chaos floor. As in Hydraotes, followed by catastrophic release as the formation these flows bank up against blocks on the chaos floor, mechanism of chaotic terrain. Variants of this model implying that if the flows are volcanic in origin, the have subsequently been detailed by a number of au- volcanism occurred after the formation of Hydaspis thors [e.g. 3,4,5]. Meresse et al.
    [Show full text]
  • No. 40. the System of Lunar Craters, Quadrant Ii Alice P
    NO. 40. THE SYSTEM OF LUNAR CRATERS, QUADRANT II by D. W. G. ARTHUR, ALICE P. AGNIERAY, RUTH A. HORVATH ,tl l C.A. WOOD AND C. R. CHAPMAN \_9 (_ /_) March 14, 1964 ABSTRACT The designation, diameter, position, central-peak information, and state of completeness arc listed for each discernible crater in the second lunar quadrant with a diameter exceeding 3.5 km. The catalog contains more than 2,000 items and is illustrated by a map in 11 sections. his Communication is the second part of The However, since we also have suppressed many Greek System of Lunar Craters, which is a catalog in letters used by these authorities, there was need for four parts of all craters recognizable with reasonable some care in the incorporation of new letters to certainty on photographs and having diameters avoid confusion. Accordingly, the Greek letters greater than 3.5 kilometers. Thus it is a continua- added by us are always different from those that tion of Comm. LPL No. 30 of September 1963. The have been suppressed. Observers who wish may use format is the same except for some minor changes the omitted symbols of Blagg and Miiller without to improve clarity and legibility. The information in fear of ambiguity. the text of Comm. LPL No. 30 therefore applies to The photographic coverage of the second quad- this Communication also. rant is by no means uniform in quality, and certain Some of the minor changes mentioned above phases are not well represented. Thus for small cra- have been introduced because of the particular ters in certain longitudes there are no good determi- nature of the second lunar quadrant, most of which nations of the diameters, and our values are little is covered by the dark areas Mare Imbrium and better than rough estimates.
    [Show full text]
  • Martian Crater Morphology
    ANALYSIS OF THE DEPTH-DIAMETER RELATIONSHIP OF MARTIAN CRATERS A Capstone Experience Thesis Presented by Jared Howenstine Completion Date: May 2006 Approved By: Professor M. Darby Dyar, Astronomy Professor Christopher Condit, Geology Professor Judith Young, Astronomy Abstract Title: Analysis of the Depth-Diameter Relationship of Martian Craters Author: Jared Howenstine, Astronomy Approved By: Judith Young, Astronomy Approved By: M. Darby Dyar, Astronomy Approved By: Christopher Condit, Geology CE Type: Departmental Honors Project Using a gridded version of maritan topography with the computer program Gridview, this project studied the depth-diameter relationship of martian impact craters. The work encompasses 361 profiles of impacts with diameters larger than 15 kilometers and is a continuation of work that was started at the Lunar and Planetary Institute in Houston, Texas under the guidance of Dr. Walter S. Keifer. Using the most ‘pristine,’ or deepest craters in the data a depth-diameter relationship was determined: d = 0.610D 0.327 , where d is the depth of the crater and D is the diameter of the crater, both in kilometers. This relationship can then be used to estimate the theoretical depth of any impact radius, and therefore can be used to estimate the pristine shape of the crater. With a depth-diameter ratio for a particular crater, the measured depth can then be compared to this theoretical value and an estimate of the amount of material within the crater, or fill, can then be calculated. The data includes 140 named impact craters, 3 basins, and 218 other impacts. The named data encompasses all named impact structures of greater than 100 kilometers in diameter.
    [Show full text]
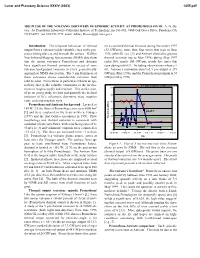
  • The Pulse of the Volcano: Discovery of Episodic Activity at Prometheus on Io
    Lunar and Planetary Science XXXIV (2003) 1455.pdf THE PULSE OF THE VOLCANO: DISCOVERY OF EPISODIC ACTIVITY AT PROMETHEUS ON IO. A. G. Da- vies. Jet Propulsion Laboratory-California Institute of Technology, ms 183-601, 4800 Oak Grove Drive, Pasadena, CA 91109-8099. (tel: 818-393-1775. email: [email protected]). Introduction: The temporal behaviour of thermal est e-corrected thermal emission during November 1997 output from a volcano yields valuable clues to the pro- (33 GW/µm), more than four times that seen in June cesses taking place at and beneath the surface. Galileo 1996 (orbit G1; see [3]) and Amirani showed its greatest Near Infrared Mapping Spectrometer (NIMS) data show thermal emission (up to May 1998) during May 1997 that the ionian volcanoes Prometheus and Amirani (orbit G8), nearly 100 GW/µm, nearly five times that have significant thermal emission in excess of non- seen during orbit G1. Including observations where e > volcanic background emission in every geometrically 60º, Amirani’s maximum observed 5 µm output is 291 appropriate NIMS observation. The 5 µm brightness of GW/µm (May 1998), and the Prometheus maximum is 54 these volcanoes shows considerable variation from GW/µm (May 1998). orbit to orbit. Prometheus in particular exhibits an epi- sodicity that yields valuable constraints to the mecha- x = time between peaks in months nisms of magma supply and eruption. This work is part 60 of an on-going study to chart and quantify the thermal 50 emission of Io’s volcanoes, determine mass eruption 9 rates, and note eruption style.
    [Show full text]
  • JPL to Map the Moon on India Mission
    I n s i d e May 19, 2006 Volume 36 Number 10 News Briefs ............... 2 Griffin Visits Lab ............ 3 Special Events Calendar ...... 2 Passings, Letters ........... 4 Spitzer Sees Comet Breakup... 2 Retirees, Classifieds ......... 4 Jet Propulsion Laborator y A JPL state-of-the-art imaging spectrometer that will provide the first high-resolution spectral map of the JPL to entire lunar surface successfully completed its critical design review this week. The Moon Mineralogy Mapper, also known as “M3,” is one of two in- materials across the surface at high spatial resolution. This data map the struments that NASA is contributing to India’s first mission to the moon, will provide a much-needed long-term baseline for future exploration scheduled to launch in late 2007 or early 2008. By mapping the mineral activities. composition of the lunar surface, the mission will both provide clues to The mission’s observations will address several important scientific moon the early development of the solar system and guide future astronauts to issues, including early evolution of the solar system; fundamental stores of precious resources. processes acting on planets that shape their character; assessment of on India Chandrayaan-1 is India’s first deep-space mission as well as its first potential impact hazards to Earth; and assessment of space resources. lunar mission. “The entire M3 team feels honored to be able to partici- From its vantage point in orbit around the moon, the spacecraft will mission pate,” said Project Manager Tom Glavich of JPL. measure the sunlight reflected by all of the rocks and soil over which The instrument is well on its way to being delivered to the Chandray- it passes.
    [Show full text]
  • POLYGONAL IMPACT CRATERS on CHARON. C.B. Beddingfield1,2, R
    51st Lunar and Planetary Science Conference (2020) 1241.pdf POLYGONAL IMPACT CRATERS ON CHARON. C.B. Beddingfield1,2, R. Beyer1,2, R.J. Cartwright1,2, K. Singer3, S. Robbins3, S.A. Stern3, V. Bray4, J.M. Moore2, K. Ennico2, C.B. Olkin3, J.R. Spencer3, H.A. Weaver5, L.A. Young3, A.Verbiscer6, J. Parker3, and the New Horizons Geology, Geophysics, and Imaging (GGI) Team; 1SETI In- stitute, Mountain View, CA, 2NASA Ames Research Center, Mountain View, CA ([email protected]), 3Southwest Research Institute, Boulder, CO, 4University of Arizona, Tucson, AZ, 5John Hopkins University Applied Physics Laboratory, Laurel, MD, 6University of Virginia, Charlottesville, VA. Introduction: Polygonal impact craters (PICs) re- flect pre-existing extensional and strike-slip faults and fractures in the target material [e.g. 1-9]. PIC straight rim segments therefore can provide important infor- mation for deciphering the tectonic histories of plane- tary bodies [e.g. 8]. The only known PIC formation mechanism is the presence of pre-existing sub-vertical structures within the target material [e.g. 5, 7, 11-13]. In contrast, circular impact craters (CICs) are in- ferred to result from impact events in non-tectonized target material. CICs can also form in pre-fractured tar- get material if the fractures are widely or closely spaced, if the fracture system is highly complex, or if the target material is covered by a thick layer of non-cohesive sed- iment that limits interactions between the impactor and the underlying bedrock/ice [e.g. 14]. Consequently, PICs and CICs are useful tools to distinguish between Fig.
    [Show full text]
  • Appendix 1: Io's Hot Spots Rosaly M
    Appendix 1: Io's hot spots Rosaly M. C. Lopes,Jani Radebaugh,Melissa Meiner,Jason Perry,and Franck Marchis Detections of plumes and hot spots by Galileo, Voyager, HST, and ground-based observations. Notes and sources . (N) NICMOS hot spots detected by Goguen etal . (1998). (D) Hot spots detected by C. Dumas etal . in 1997 and/or 1998 (pers. commun.). Keck are hot spots detected by de Pater etal . (2004) and Marchis etal . (2001) from the Keck telescope using Adaptive Optics. (V, G, C) indicate Voyager, Galileo,orCassini detection. Other ground-based hot spots detected by Spencer etal . (1997a). Galileo PPR detections from Spencer etal . (2000) and Rathbun etal . (2004). Galileo SSIdetections of hot spots, plumes, and surface changes from McEwen etal . (1998, 2000), Geissler etal . (1999, 2004), Kezthelyi etal. (2001), and Turtle etal . (2004). Galileo NIMS detections prior to orbit C30 from Lopes-Gautier etal . (1997, 1999, 2000), Lopes etal . (2001, 2004), and Williams etal . (2004). Locations of surface features are approximate center of caldera or feature. References de Pater, I., F. Marchis, B. A. Macintosh, H. G. Rose, D. Le Mignant, J. R. Graham, and A. G. Davies. 2004. Keck AO observations of Io in and out of eclipse. Icarus, 169, 250±263. 308 Appendix 1: Io's hot spots Goguen, J., A. Lubenow, and A. Storrs. 1998. HST NICMOS images of Io in Jupiter's shadow. Bull. Am. Astron. Assoc., 30, 1120. Geissler, P. E., A. S. McEwen, L. Keszthelyi, R. Lopes-Gautier, J. Granahan, and D. P. Simonelli. 1999. Global color variations on Io. Icarus, 140(2), 265±281.
    [Show full text]
  • Orbital Evidence for More Widespread Carbonate- 10.1002/2015JE004972 Bearing Rocks on Mars Key Point: James J
    PUBLICATIONS Journal of Geophysical Research: Planets RESEARCH ARTICLE Orbital evidence for more widespread carbonate- 10.1002/2015JE004972 bearing rocks on Mars Key Point: James J. Wray1, Scott L. Murchie2, Janice L. Bishop3, Bethany L. Ehlmann4, Ralph E. Milliken5, • Carbonates coexist with phyllosili- 1 2 6 cates in exhumed Noachian rocks in Mary Beth Wilhelm , Kimberly D. Seelos , and Matthew Chojnacki several regions of Mars 1School of Earth and Atmospheric Sciences, Georgia Institute of Technology, Atlanta, Georgia, USA, 2The Johns Hopkins University/Applied Physics Laboratory, Laurel, Maryland, USA, 3SETI Institute, Mountain View, California, USA, 4Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, California, USA, 5Department of Geological Sciences, Brown Correspondence to: University, Providence, Rhode Island, USA, 6Lunar and Planetary Laboratory, University of Arizona, Tucson, Arizona, USA J. J. Wray, [email protected] Abstract Carbonates are key minerals for understanding ancient Martian environments because they Citation: are indicators of potentially habitable, neutral-to-alkaline water and may be an important reservoir for Wray, J. J., S. L. Murchie, J. L. Bishop, paleoatmospheric CO2. Previous remote sensing studies have identified mostly Mg-rich carbonates, both in B. L. Ehlmann, R. E. Milliken, M. B. Wilhelm, Martian dust and in a Late Noachian rock unit circumferential to the Isidis basin. Here we report evidence for older K. D. Seelos, and M. Chojnacki (2016), Orbital evidence for more widespread Fe- and/or Ca-rich carbonates exposed from the subsurface by impact craters and troughs. These carbonates carbonate-bearing rocks on Mars, are found in and around the Huygens basin northwest of Hellas, in western Noachis Terra between the Argyre – J.
    [Show full text]