Temporal Evolution of Flow-Like Landslide Hazard for a Road
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Linea 34 ACCIAROLI - S
Linea 34 ACCIAROLI - S. MARIA DI CASTELLABATE - AGROPOLI - SALERNO (VINCIPROVA) DAL 14/09/2015 FERIALE Acciaroli - Agnone - Casa del Conte - S. Marco di Castellabate - S. Maria di Castellabate - Agropoli - Paestum - Capaccio - Bivio S. Cecilia - Battipaglia – Salerno FS/C.so Garibaldi. Percorso estivo per Napoli: Acciaroli - Agnone - Casa del Conte - S. Marco di Castellabate – S. Maria di Castellabate – Agropoli – Paestum – Capaccio – Bivio S. Cecilia – Battipaglia Autostrada A3 RC/SA – Napoli Via G. Ferraris - P.zza Garibaldi – C. so Umberto I – Via De Pretis - P.zza Municipio Validità 02 23 32 27 02 02 04 23 09 09 23 02 04 02 02 02 02 02 02 23 02 23 17 02 04 GALDO (CAP.) 6.20 7.00 15.05 17.35 ACCIAROLI PORTO 5.20 6.40 7.25 8.50 9.50 9.50 12.50 15.30 16.20 17.50 18.00 18.50 20.10 MONTECORICE 5.32 6.52 7.37 9.02 10.02 10.02 13.02 15.42 16.32 18.02 19.02 20.22 S. MARCO DI C.TE 5.44 5.45 6.35 6.35 7.05 7.50 9.20 9.20 10.15 10.15 12.55 13.30 13.30 14.20 15.20 15.55 16.50 18.20 18.20 18.55 19.15 20.35 S. MARIA DI C.TE 5.50 5.50 6.40 6.40 7.10 7.30 7.55 9.30 9.30 10.30 10.30 11.30 13.00 13.35 14.30 15.30 16.00 17.00 18.30 18.25 19.00 19.30 20.40 AGROPOLI TENDOSTR. -

Autostrada A3 Salerno-Reggio Calabria Apertura Al Traffico Del Viadotto ‘Italia’ Macrolotto 3.2
L’Italia si fa strada Autostrada A3 Salerno-Reggio Calabria Apertura al traffico del viadotto ‘Italia’ Macrolotto 3.2 Intervento del Presidente di Anas S.p.A. Ing. Gianni Vittorio Armani Laino Castello (CS), 26 luglio 2016 Autostrada A3 Salerno-Reggio Calabria Ci siamo… Per la prima volta l’esodo estivo su una nuova autostrada interamente percorribile su entrambe le carreggiate #A3EsodoZeroCantieri Apertura al traffico del viadotto ‘Italia’ – A3 SA-RC Macrolotto 3.2 2 26 luglio 2016 Autostrada A3 Salerno-Reggio Calabria Pesante eredità del passato, nonostante oggi sia un’autostrada moderna, sicura e confortevole 443 km 118 km 30 km Campania Basilicata 295 km 1050 m slm Calabria L’autostrada più alta d’Europa L’unica autostrada (fino a 1050 m s.l.m..) della regione Calabria Apertura al traffico del viadotto ‘Italia’ – A3 SA-RC Macrolotto 3.2 3 26 luglio 2016 Autostrada A3 Salerno-Reggio Calabria Una grande sfida italiana e una grande opera per il Mezzogiorno Apertura al traffico del viadotto ‘Italia’ – A3 SA-RC Macrolotto 3.2 4 26 luglio 2016 Impegno Anas Mezzogiorno Piano pluriennale 2015-2019 investimento totale di 20,2 miliardi di euro Maggiori investimenti al SUD Motivi • Maggior parte rete Anas 37% + 63% nel Mezzogiorno • Gap infrastrutturale Nord-Sud € 7,4 miliardi € 12,8 miliardi Centro-Nord Sud-Isole Apertura al traffico del viadotto ‘Italia’ – A3 SA-RC Macrolotto 3.2 5 26 luglio 2016 Autostrada A3 Salerno-Reggio Calabria L’intero tracciato autostradale di 443 km è percorribile su 3 e 2 corsie per senso di marcia L’apertura di oggi della carreggiata nord del viadotto ‘Italia’ rende fruibili al traffico 20 km di nuovo tracciato autostradale tra Laino Borgo e Campotenese, di cui 10 realizzati ex novo Resta da completare un tratto di circa 600 metri in corrispondenza della galleria ‘Laria’, in costruzione, che sarà pronto per il prossimo dicembre. -

Salerno-Reggio Calabria, Sono Previsti, Nei Giorni Critici
Esodo Estivo 2015 Esodo estivo 2015 Il piano esodo ANAS e le risorse Il Piano operativo di gestione predisposto dall’Anas per l’esodo estivo 2015 ha i seguenti obiettivi: . ridurre e comunque minimizzare i disagi all’utenza; . innalzare i livelli di sicurezza; . rendere tempestiva l’assistenza e il soccorso; . diffondere una corretta ed efficace informazione. Per far questo l’Anas ha svolto le seguenti attività: . individuare i cantieri inamovibili; . predisporre una viabilità alternativa in corrispondenza dei cantieri inamovibili (dove possibile); . predisporre un calendario del traffico incentrato sull’individuazione dei “giorni critici”; . condividere le procedure operative e definire i codici di emergenza con i soggetti istituzionali coinvolti nella gestione della viabilità; . monitorare 24 ore su 24 il traffico sulla rete stradale nazionale; . utilizzare di piani di comunicazione per l’utenza. Nel periodo dell’esodo estivo l’Anas impiegherà, in turnazione, circa 2.500 unità e oltre 1070 automezzi. Saranno in funzione sulla rete Anas circa 1800 telecamere e 300 Pannelli a Messaggio Variabile (con indicazione, in alcuni tratti, del tempo medio di percorrenza). L’attività del personale sarà focalizzata verso i servizi di viabilità e traffico, pattugliamento dei percorsi alternativi e presidio di snodi, assistenza e soccorso agli utenti, ordine e sicurezza, operazioni che Anas svolge anche con l’ausilio della tecnologia “ITS” (Intelligent Traffic System) che usa telecamere, videowall, sensori di traffico, contatori veicolari e centraline rilevamento meteo. Tutte le informazioni raccolte verranno gestite dalle 20 Sale Operative Compartimentali e dalla Sala Operativa Nazionale (in funzione h24) che pianificano interventi e azioni per la regolazione dei flussi del traffico, in contatto diretto con il Centro di Coordinamento Nazionale in Materia di Viabilità (Viabilità Italia) istituito presso il Ministero dell’Interno – Servizio Polizia Stradale e, in casi di emergenza, con il Dipartimento Nazionale della Protezione Civile. -

Atti Parlamentari
Camera dei Deputati – 49 – Senato della Repubblica XVII LEGISLATURA - DISEGNI DI LEGGE E RELAZIONI - DOCUMENTI - DOC. CCXIX N. 5 AIl.C STRADA A SCORRIMENTO VELOCE CALITRI - PESCOPAGANO - RAPONE - CASTELGRANDE - MURO LUCANO - BARAGIANO LEGENDA - \' LOno: COmpletato in esercizio _ 't LOTTO il """" ci ltOCUliono: Invito..,tklpltalfl!l.-lIt/f17/'lC1J.C _ Y LOTTO PRIIl VIadotto I SWw;oio ci CosteIp1de c...QaMa 01 KnùO+5IìO C""*<Nia 01 1Ctrù2+498 CMIcO'fiO al Km26+98J In corso di esecuzione Y LOTTO - 'Z STRN..ClO: S't'KOlO 01 liIJRO lJJCAHO Appronu PTosMtuloP.".....nare.. • "'_JI"O*'-"""'--.IIJWOAlt _ Tratto Muro lucano..Bacagiano complelato ed in esercizio Tratto in esercizjo (comsrendente v_tto sul fiume Ptltano} __.... ".100 :r lJlII1) f SIJIOIa) '... ... • ••r------, ... lViadotto Platano I Baraglano-Balvano In eaerclzlo Direzione Rac;e. Autoatradala Pl - Sicignano Camera dei Deputati – 50 – Senato della Repubblica XVII LEGISLATURA - DISEGNI DI LEGGE E RELAZIONI - DOCUMENTI - DOC. CCXIX N. 5 ALL. D ....f/ 0'6" g;: 20'.9/b2 are//e !!JP6t?ion6 STRADA A S.V. LlONI- GROTIAMINARDA PER IL COLLEGAMENTO DELL'AUTOSTRADA A3 SA - RC (Svincolo di Contursi) CON L'AUTOSTRADA A16 NA - BA (Svincolo di Grottaminarda) Amministrazjone Aggiudicatrice: Commissario ad Acta ex Art.86 L. 289/02 - Ministero dello Sviluppo Economico Importo Progetto: 430 ML € 1. Descrizione e obiettivi dell'infrastruttura Lioni - Grottaminarda (euro 430 milioni) L'infrastruttura viaria Lioni Grottaminarda costituisce il completamento del collegamento, già in parte realizzato, tra la A16 Napoli - Bari e la A3 Salerno - Reggio Calabria e fa parte dell'itinerario più ampio Agropoli - Contursi - Grottaminarda - Termoli, che parte da Contursi Terme raggiungendo Lioni con la SS 691, nota anche come strada a scorrimento veloce Fondo Valle del Sele, prosegue fino a Grottaminarda (Strada a S.V. -
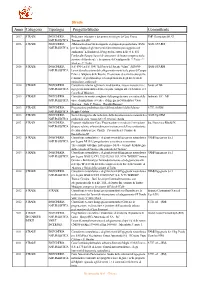
Elenco Progetti
Strade Anno Categoria Tipologia Progetto/Studio Committente 2017 STRADE INGEGNERIA Redazione relazione e documenti tecnici per la Gara “Frana PMP Costruzioni Srl AT NATURALISTICA Tramonti SA SP1” 2016 STRADE INGEGNERIA Affidamento di servizi di supporto al gruppo di progettazione ANAS ANAS SPA RM NATURALISTICA per lo sviluppo degli ‘interventi di inserimento paesaggistico ed ambientale’ nell’ambito del Progetto Esecutivo della “S.S. 652 Fondovalle Sangro. Lavori di costruzione del tratto compreso tra la stazione di Gamberale e la stazione di Civitaluparella. 2° Lotto - 2° Stralcio - 2° Tratto” 2016 STRADE INGEGNERIA S.S. 696 (ex S.S. 584) “del Parco del Sirente Velino”. AQ30/05- ANAS SPA RM NATURALISTICA Lavori di realizzazione del collegamento viario tra la piana di Campo Felice e l’altipiano delle Rocche. Prestazione di servizi tecnici per la redazione degli elaborati per il completamento degli interventi di mitigazione ambientale. 2014 STRADE INGEGNERIA Consulenza relativa agli interventi di bonifica, messa in sicurezza e Lande srl NA NATURALISTICA ingegneria naturalistica della scarpata contigua alle ex Scuderie del Castello di Miramare 2013 STRADE INGEGNERIA Consulenza in merito a migliorie della progettazione esecutiva delle Ambiente S.C. MS NATURALISTICA opere di mitigazione a verde e di Ingegneria Naturalistica “Gara Siracusa – Gela 2° Tronco – Rosolini Ragusa”. 2013 STRADE INGEGNERIA Progettazione preliminare fossi del macrolotto 6 della Salerno- S.T.E. Srl RM NATURALISTICA Reggio Calabria 2013 STRADE INGEGNERIA Servizi di supporto alla redazione della documentazione naturalistica ANAS SpA RM NATURALISTICA ambientale gara “nuova SS 125 Orientale Sarda 2013 STRADE INGEGNERIA Proposte migliorative Gara “Progettazione esecutiva e l’esecuzione Ing. Francesco Riboldi NA NATURALISTICA di opere relative ai lavori di messa in sicurezza dell’area sottostante il centro abitato in Loc. -

Atti Parlamentari
Repubblica – 17 – Camen" ( ( eTè LA TURA - DISEGN rn (CUMENTI - DOC. ART - Terzo Rapporto Annuale al Parlamento li 2015 si configura pertanto come secondo anno consecutivo di crescita dopo la contra zione del 2012 e 2013. Roma Fiu mi ci no 40.4 63.208 2 Mi lano Mal pensa 18.582.043 3 ilerga mo l0.404.625 4 Mila nli Li nate 9.689.63 5 5 Venezi a 8.751 .028' 6 Catania 7 .105.487 7 flolllgTIH 6.889.742 8 Napl1li 6. 163. 188 9 Roma Ciampino 5.834.201 10 Palem10 4.9 10.79 1 11 l'i8il 4.804.774 12 Ba ri 3.972. IUS 13 Caglia ri 3.71 9.289 14 Torinn 3.666.58 2 15 Verona 2.591.255 Tabella 7. Primi 15 aeroporti italiani ordinati in base al numero di ·passeggeri trasportati nel 2015. Fonte: Assacroporti Co me nel 2013 e 2014, anche nel 2015 gli sca li di Roma Fiu micino, Milano Malpensa, Milano Li nate, Be rga mo e Venezia si co nfermano come i primi ci nque aeroporti Italiani per numero di passeggeri e movimenti. Inoltre, per i primi quattro aeroporti t ransita il 50% del passeggeri in Itali a. Nel 2015 si confermano le osservaz ioni degli anni precedenti: la maggior pa rte degli sca li movi menta un volume passeggeri compreso tra i 2 e gli 8 milioni, e il primo sca lo per volume passeggeri, Ro ma (Fiumicino e Ciampino) di stanzia nettamente la seconda cla ss ificata, M ilano (Malpensa e Li nat e), con un divario ch e continua ad aumentare anch e nel 2015. -

Pianificazione Invernale
Pianificazione Invernale Edizione 2011-2012 PIANIFICAZIONE INVERNALE PER LA GESTIONE DELLA VIABILITA’ E REGOLAMENTAZIONE DELLA CIRCOLAZIONE DEI MEZZI PESANTI IN AUTOSTRADA IN CASO DI PRECIPITAZIONI NEVOSE * EDIZIONE 2011‐2012 * 1.Premessa Gli interventi finalizzati alla gestione delle emergenze che interessano il sistema viario autostradale determinate da precipitazioni nevose sono disciplinate dai seguenti atti: 1. le “Linee guida per la gestione coordinata delle emergenze invernali su aree geografiche vaste con interessamento di più concessionarie autostradali”, documento redatto congiuntamente da Polizia Stradale, Anas ed Aiscat; 2. le pianificazioni redatte a livello locale (Regioni, Uffici Territoriali di Governo, Compartimenti della Polizia Stradale, Concessionarie Autostradali, Anas come gestore autostradale e della viabilità statale); 3. il “Protocollo Operativo per la regolamentazione della circolazione dei veicoli pesanti in autostrada in presenza di neve”, siglato in data 14 dicembre 2005 presso l’allora Ministero delle Infrastrutture e Trasporti e sottoscritto dai rappresentanti del predetto dicastero, del Ministero dell’Interno, dell’Anas, dell’Aiscat, delle associazioni degli autotrasportatori; 4. gli schemi segnaletici di attuazione del filtraggio dinamico (oggi definito fermo temporaneo) in carreggiata dei veicoli con massa superiore alle 7,5 t, redatti a corredo del “Protocollo Operativo per la regolamentazione della circolazione dei veicoli pesanti in autostrada in presenza di neve”, rivisitati con la condivisione del -

Progetto Relazione Finanziaria Annuale Al 31 Dicembre 2020
SOCIETÀ SOGGETTA ALL’ATTIVITÀ DI DIREZIONE E DI COORDINAMENTO DI AUTOSTRADE PER L’ITALIA S.P.A. Progetto Relazione Finanziaria Annuale al 31 dicembre 2020 Assemblea Ordinaria del 8 – 9 aprile 2021 Sede Legale in Napoli, Via G. Porzio n. 4 Centro Direzionale is. A/7 Capitale Sociale Euro 9.056.250,00 interamente versato Iscrizione al Registro delle Imprese di Napoli e Codice Fiscale n. 00658460639 1 Sommario Pag Convocazione Assemblea Ordinaria 4 1. Introduzione Organi sociali per gli esercizi 2018, 209 e 2020 12 Autostrade Meridionali in Borsa 14 Principali dati economico – finanziari 15 2. Relazione sulla gestione Indicatori alternativi di performance 17 Andamento economico – finanziario 21 Richiesta della consob di diffusione di informazioni ai sensi dell’art. 114, comma 5, del d.lgs. N° 31 58/1998 (tuf) Andamento gestionale Traffico 44 Tariffe 45 Potenziamento ed ammodernamento della rete 52 Gestione operativa della rete 55 Risorse umane 58 Governance societaria 60 Altre informazioni 62 Informazioni sugli assetti proprietari 63 Rapporti con Società Controllante e Correlate 65 Eventi significativi in ambito regolatorio 66 Valutazione in merito alla continuità aziendale ed Evoluzione prevedibile della gestione 68 Valutazione e gestione dei principali rischi di Autostrade Meridionali 75 Eventi successivi al 31 dicembre 2020 81 2 Proposte all’Assemblea 82 3. Bilancio dell’esercizio chiuso al 31 dicembre 2020 Prospetti Contabili 84 Situazione patrimoniale – finanziaria 85 Conto Economico 86 Conto Economico complessivo 87 Prospetto delle variazioni di patrimonio netto 87 Rendiconto Finanziario 88 Note illustrative 89 Aspetti di carattere generale 90 Forma e contenuto del bilancio 99 Principi contabili utilizzati 101 Informazioni sulle voci della Situazione patrimoniale – finanziaria 117 Informazioni su Conto Economico 135 Effetti emergenza Coronavirus 141 Utile per azione 142 Altre informazioni 143 Rapporti con parti correlate 151 Prospetto riepilogativo dei dati essenziali dell’ultimo bilancio di Autostrade per l’Italia S.p.A. -

Three New Alien Taxa for Europe and a Chorological Update on the Alien Vascular Flora of Calabria (Southern Italy)
plants Article Three New Alien Taxa for Europe and a Chorological Update on the Alien Vascular Flora of Calabria (Southern Italy) 1, 1, , 2 Valentina Lucia Astrid Laface y , Carmelo Maria Musarella * y , Ana Cano Ortiz , Ricardo Quinto Canas 3,4 , Serafino Cannavò 1 and Giovanni Spampinato 1 1 Department of AGRARIA, Mediterranean University of Reggio Calabria, Loc. Feo di Vito snc, 89122 Reggio Calabria, Italy; [email protected] (V.L.A.L.); serafi[email protected] (S.C.); [email protected] (G.S.) 2 Department of Animal and Plant Biology and Ecology, Section of Botany, University of Jaén, 23071 Jaén, Spain; [email protected] 3 Faculty of Sciences and Technology, University of Algarve, Campus de Gambelas, 8005-139 Faro, Portugal; [email protected] 4 Centre of Marine Sciences (CCMAR), University of Algarve, Campus de Gambelas, 8005-139 Faro, Portugal * Correspondence: [email protected] These authors contributed equally to the work. y Received: 27 June 2020; Accepted: 8 September 2020; Published: 11 September 2020 Abstract: Knowledge on alien species is needed nowadays to protect natural habitats and prevent ecological damage. The presence of new alien plant species in Italy is increasing every day. Calabria, its southernmost region, is not yet well known with regard to this aspect. Thanks to fieldwork, sampling, and observing many exotic plants in Calabria, here, we report new data on 34 alien taxa. In particular, we found three new taxa for Europe (Cascabela thevetia, Ipomoea setosa subsp. pavonii, and Tecoma stans), three new for Italy (Brugmansia aurea, Narcissus ‘Cotinga’, and Narcissus ‘Erlicheer’), one new one for the Italian Peninsula (Luffa aegyptiaca), and 21 new taxa for Calabria (Allium cepa, Asparagus setaceus, Bassia scoparia, Beta vulgaris subsp. -

Anas Pronta a Realizzare I Raccordi Alla Rete Stradale Ed Autostradale’
Published on Anas S.p.A. (https://www.stradeanas.it) Home > Ponte di Messina, Pozzi: ‘Anas pronta a realizzare i raccordi alla rete stradale ed autostradale’ Sicilia, Palermo, 27/11/2003 Ponte di Messina, Pozzi: ‘Anas pronta a realizzare i raccordi alla rete stradale ed autostradale’ Oggi firmato a Palazzo Chigi l’Accordo di programma. Entro il 2011 completati lavori Sa-Rc, autostrade siciliane, Palermo-Messina e Nuova Statale Jonica “L’Anas è pronta a realizzare i raccordi del Ponte di Messina alla rete stradale e autostradale. L’Accordo di Programma firmato oggi a Palazzo Chigi è un altro importante passo in avanti verso la realizzazione del Ponte sullo Stretto, che ha un valore logistico internazionale, essendo una delle poche maglie mancanti del corridoio n. 1 Berlino-Reggio Calabria-Palermo”. E’ quanto ha dichiarato il Presidente dell’Anas Spa Vincenzo Pozzi. “L’Anas Spa partecipa con una quota di circa l’8% alla società Ponte sullo Stretto, quota che è pronta a far salire fino al 15%, ed è fiera di aver contribuito a sbloccare questa opera fondamentale per il sistema trasportistico italiano, avendo parte attiva nell’approvazione del progetto preliminare e nei vari passaggi societari”, ha affermato Il Presidente dell’Anas. “Il Ponte ha bisogno di essere collegato a tutta la complessa rete intermodale dei trasporti. Per quanto riguarda la rete stradale e autostradale, l’accordo di programma individua i raccordi necessari a consentire l`operatività del ponte, e il progetto preliminare prevede che si sviluppino in massima parte in galleria, con elevati benefici ambientali e paesaggistici”, ha continuato Pozzi. -

Financial Statements As at 31 December 2016
Company subject to the management and control of Atlantia S.p.A. Financial Statements as at 31 December 2012012016201 666 Headquarters - 00159 Rome, Via Giuseppe Donati n° 174 Share Capital € 10,116,452.45 fully paid-up Registration no. in the Rome Companies Register and Internal Revenue Code 00481670586 VAT Code 00904791001, E.A.R. no. 526702 TABLE OF CONTENTS Page Social authorities 3 Management report General concerns 5 Portofolio of works 12 Summary of financial and equity management results - Introduction 13 - Highlights 14 - Economic management 16 - Equity structure 19 Investments 22 Research and development 22 Quality system 23 Human resources 24 Relations with subsidiary companies and Consortiums 27 Registered office and main operating units 34 Management perspective evolution 35 Information according to art. 2428 of the Italian Civil Code paragraph 3 point 6-bis 36 Information related to the application of Italian Legislative Decree N. 196/03 37 Information related to the application of Italian Legislative Decree. N. 231/01 38 THE FINANCIAL STATEMENTS BALANCE SHEET, INCOME STATEMENT AND CASH FLOW STATEMENT(prospects) 41 NOTES TO THE FINANCIAL STATEMENTS General overview 51 Structure and contents of the financial statements 52 Accounting standards and evaluation criteria 53 BALANCE SHEET INFORMATION 62 INCOME STATEMENT INFORMATION 97 Cash flow statement 113 Guarantees and risks 114 Related parties transactions 116 Obligations with buy back provision 123 Financial lease transactions 123 Significant events occurring after financial year end 123 Summary of basic data of the last financial statements of the company that performs management and coordination activities (Atlantia S.p.A.) 124 General Meeting proposals 125 F.T.A. -

Autostrada A3 `Salerno Reggio Calabria`, Anas: Per Lavori, Limitazioni Al Traffico Su Alcuni Tratti Nelle Province Di Reggio Calabria E Cosenza
Published on Anas S.p.A. (https://www.stradeanas.it) Home > Autostrada A3 `Salerno Reggio Calabria`, Anas: per lavori, limitazioni al traffico su alcuni tratti nelle province di Reggio Calabria e Cosenza Calabria, Cosenza, 26/01/2016 Autostrada A3 `Salerno Reggio Calabria`, Anas: per lavori, limitazioni al traffico su alcuni tratti nelle province di Reggio Calabria e Cosenza Anas comunica che, per il prosieguo dei lavori di realizzazione della nuova autostrada, sulla A3 `Salerno- Reggio Calabria sarà prorogata fino al prossimo 22 febbraio 2016 la chiusura della terza carreggiata per la Sicilia (dal km 0,950 al km 1,600) tra i territori comunali di Scilla, Villa San Giovanni e Campo Calabro, in provincia di Reggio Calabria. Verrà, infatti, riaperto al traffico il tratto compreso tra il km 0,390 ed il km 0,950. Il traffico veicolare in direzione di Villa San Giovanni/imbarchi per la Sicilia verrà deviato sulla vecchia carreggiata nord. Inoltre, per il prosieguo dei lavori di ammodernamento del Macrolotto 3.2, a partire da giovedì 28 gennaio 2016 e fino al 15 febbraio 2016 sarà in vigore la chiusura, parziale, della rampa bidirezionale di collegamento tra lo svincolo di Mormanno (al km 163,000) e la viabilità minore, con deviazione del traffico in uscita in direzione Reggio Calabria sulla rampa provvisoria lungo la strada provinciale 3 `Mormanno- Papasidero Scalea`, nel territorio comunale di Mormanno, in provincia di Cosenza. All`approssimarsi delle aree di cantiere vigerà il limite di velocità di 30 km/h ed il divieto di sorpasso per tutti gli autoveicoli. Anas raccomanda prudenza nella guida e ricorda che l`evoluzione della situazione del traffico in tempo reale è consultabile sul sito web www.stradeanas.it [1] oppure su tutti gli smartphone e i tablet, grazie all`applicazione `VAI Anas Plus`, disponibile gratuitamente in `App store` e in `Play store`.