Accelerating Phylogeny-Aware Short DNA Read Alignment with Fpgas
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HMMER User's Guide
HMMER User's Guide Biological sequence analysis using pro®le hidden Markov models http://hmmer.wustl.edu/ Version 2.1.1; December 1998 Sean Eddy Dept. of Genetics, Washington University School of Medicine 4566 Scott Ave., St. Louis, MO 63110, USA [email protected] With contributions by Ewan Birney ([email protected]) Copyright (C) 1992-1998, Washington University in St. Louis. Permission is granted to make and distribute verbatim copies of this manual provided the copyright notice and this permission notice are retained on all copies. The HMMER software package is a copyrighted work that may be freely distributed and modi®ed under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version. Some versions of HMMER may have been obtained under specialized commercial licenses from Washington University; for details, see the ®les COPYING and LICENSE that came with your copy of the HMMER software. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the Appendix for a copy of the full text of the GNU General Public License. 1 Contents 1 Tutorial 5 1.1 The programs in HMMER . 5 1.2 Files used in the tutorial . 6 1.3 Searching a sequence database with a single pro®le HMM . 6 HMM construction with hmmbuild . 7 HMM calibration with hmmcalibrate . 7 Sequence database search with hmmsearch . 8 Searching major databases like NR or SWISSPROT . -

Apply Parallel Bioinformatics Applications on Linux PC Clusters
Tunghai Science Vol. : 125−141 125 July, 2003 Apply Parallel Bioinformatics Applications on Linux PC Clusters Yu-Lun Kuo and Chao-Tung Yang* Abstract In addition to the traditional massively parallel computers, distributed workstation clusters now play an important role in scientific computing perhaps due to the advent of commodity high performance processors, low-latency/high-band width networks and powerful development tools. As we know, bioinformatics tools can speed up the analysis of large-scale sequence data, especially about sequence alignment. To fully utilize the relatively inexpensive CPU cycles available to today’s scientists, a PC cluster consists of one master node and seven slave nodes (16 processors totally), is proposed and built for bioinformatics applications. We use the mpiBLAST and HMMer on parallel computer to speed up the process for sequence alignment. The mpiBLAST software uses a message-passing library called MPI (Message Passing Interface) and the HMMer software uses a software package called PVM (Parallel Virtual Machine), respectively. The system architecture and performances of the cluster are also presented in this paper. Keywords: Parallel computing, Bioinformatics, BLAST, HMMer, PC Clusters, Speedup. 1. Introduction Extraordinary technological improvements over the past few years in areas such as microprocessors, memory, buses, networks, and software have made it possible to assemble groups of inexpensive personal computers and/or workstations into a cost effective system that functions in concert and posses tremendous processing power. Cluster computing is not new, but in company with other technical capabilities, particularly in the area of networking, this class of machines is becoming a high-performance platform for parallel and distributed applications [1, 2, 11, 12, 13, 14, 15, 16, 17]. -

HMMER User's Guide
HMMER User’s Guide Biological sequence analysis using profile hidden Markov models http://hmmer.org/ Version 3.0rc1; February 2010 Sean R. Eddy for the HMMER Development Team Janelia Farm Research Campus 19700 Helix Drive Ashburn VA 20147 USA http://eddylab.org/ Copyright (C) 2010 Howard Hughes Medical Institute. Permission is granted to make and distribute verbatim copies of this manual provided the copyright notice and this permission notice are retained on all copies. HMMER is licensed and freely distributed under the GNU General Public License version 3 (GPLv3). For a copy of the License, see http://www.gnu.org/licenses/. HMMER is a trademark of the Howard Hughes Medical Institute. 1 Contents 1 Introduction 5 How to avoid reading this manual . 5 How to avoid using this software (links to similar software) . 5 What profile HMMs are . 5 Applications of profile HMMs . 6 Design goals of HMMER3 . 7 What’s still missing in HMMER3 . 8 How to learn more about profile HMMs . 9 2 Installation 10 Quick installation instructions . 10 System requirements . 10 Multithreaded parallelization for multicores is the default . 11 MPI parallelization for clusters is optional . 11 Using build directories . 12 Makefile targets . 12 3 Tutorial 13 The programs in HMMER . 13 Files used in the tutorial . 13 Searching a sequence database with a single profile HMM . 14 Step 1: build a profile HMM with hmmbuild . 14 Step 2: search the sequence database with hmmsearch . 16 Searching a profile HMM database with a query sequence . 22 Step 1: create an HMM database flatfile . 22 Step 2: compress and index the flatfile with hmmpress . -

Software List for Biology, Bioinformatics and Biostatistics CCT
Software List for biology, bioinformatics and biostatistics v CCT - Delta Software Version Application short read assembler and it works on both small and large (mammalian size) ALLPATHS-LG 52488 genomes provides a fast, flexible C++ API & toolkit for reading, writing, and manipulating BAMtools 2.4.0 BAM files a high level of alignment fidelity and is comparable to other mainstream Barracuda 0.7.107b alignment programs allows one to intersect, merge, count, complement, and shuffle genomic bedtools 2.25.0 intervals from multiple files Bfast 0.7.0a universal DNA sequence aligner tool analysis and comprehension of high-throughput genomic data using the R Bioconductor 3.2 statistical programming BioPython 1.66 tools for biological computation written in Python a fast approach to detecting gene-gene interactions in genome-wide case- Boost 1.54.0 control studies short read aligner geared toward quickly aligning large sets of short DNA Bowtie 1.1.2 sequences to large genomes Bowtie2 2.2.6 Bowtie + fully supports gapped alignment with affine gap penalties BWA 0.7.12 mapping low-divergent sequences against a large reference genome ClustalW 2.1 multiple sequence alignment program to align DNA and protein sequences assembles transcripts, estimates their abundances for differential expression Cufflinks 2.2.1 and regulation in RNA-Seq samples EBSEQ (R) 1.10.0 identifying genes and isoforms differentially expressed EMBOSS 6.5.7 a comprehensive set of sequence analysis programs FASTA 36.3.8b a DNA and protein sequence alignment software package FastQC -
PTIR: Predicted Tomato Interactome Resource
www.nature.com/scientificreports OPEN PTIR: Predicted Tomato Interactome Resource Junyang Yue1,*, Wei Xu1,*, Rongjun Ban2,*, Shengxiong Huang1, Min Miao1, Xiaofeng Tang1, Guoqing Liu1 & Yongsheng Liu1,3 Received: 15 October 2015 Protein-protein interactions (PPIs) are involved in almost all biological processes and form the basis Accepted: 08 April 2016 of the entire interactomics systems of living organisms. Identification and characterization of these Published: 28 April 2016 interactions are fundamental to elucidating the molecular mechanisms of signal transduction and metabolic pathways at both the cellular and systemic levels. Although a number of experimental and computational studies have been performed on model organisms, the studies exploring and investigating PPIs in tomatoes remain lacking. Here, we developed a Predicted Tomato Interactome Resource (PTIR), based on experimentally determined orthologous interactions in six model organisms. The reliability of individual PPIs was also evaluated by shared gene ontology (GO) terms, co-evolution, co-expression, co-localization and available domain-domain interactions (DDIs). Currently, the PTIR covers 357,946 non-redundant PPIs among 10,626 proteins, including 12,291 high-confidence, 226,553 medium-confidence, and 119,102 low-confidence interactions. These interactions are expected to cover 30.6% of the entire tomato proteome and possess a reasonable distribution. In addition, ten randomly selected PPIs were verified using yeast two-hybrid (Y2H) screening or a bimolecular fluorescence complementation (BiFC) assay. The PTIR was constructed and implemented as a dedicated database and is available at http://bdg.hfut.edu.cn/ptir/index.html without registration. The increasing number of complete genome sequences has revealed the entire structure and composition of proteins, based mainly on theoretical predictions utilizing their corresponding DNA sequences. -
Scaling HMMER Performance on Multicore Architectures
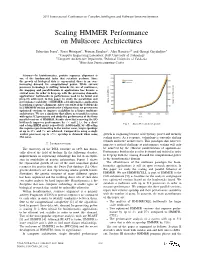
2011 International Conference on Complex, Intelligent, and Software Intensive Systems Scaling HMMER Performance on Multicore Architectures Sebastian Isaza∗, Ernst Houtgast∗, Friman Sanchezy, Alex Ramirezyz and Georgi Gaydadjiev∗ ∗Computer Engineering Laboratory, Delft University of Technology yComputer Architecture Department, Technical University of Catalonia zBarcelona Supercomputing Center Abstract—In bioinformatics, protein sequence alignment is one of the fundamental tasks that scientists perform. Since the growth of biological data is exponential, there is an ever- increasing demand for computational power. While current processor technology is shifting towards the use of multicores, the mapping and parallelization of applications has become a critical issue. In order to keep up with the processing demands, applications’ bottlenecks to performance need to be found and properly addressed. In this paper we study the parallelism and performance scalability of HMMER, a bioinformatics application to perform sequence alignment. After our study of the bottlenecks in a HMMER version ported to the Cell processor, we present two optimized versions to improve scalability in a larger multicore architecture. We use a simulator that allows us to model a system with up to 512 processors and study the performance of the three parallel versions of HMMER. Results show that removing the I/O bottleneck improves performance by 3× and 2:4× for a short Fig. 1. Swiss-Prot database growth. and a long HMM query respectively. Additionally, by offloading the sequence pre-formatting to the worker cores, larger speedups of up to 27× and 7× are achieved. Compared to using a single worker processor, up to 156× speedup is obtained when using growth is stagnating because of frequency, power and memory 256 cores. -
![Downloaded from TAIR10 [27]](https://docslib.b-cdn.net/cover/0240/downloaded-from-tair10-27-1950240.webp)
Downloaded from TAIR10 [27]
The Author(s) BMC Bioinformatics 2017, 18(Suppl 12):414 DOI 10.1186/s12859-017-1826-2 RESEARCH Open Access A sensitive short read homology search tool for paired-end read sequencing data Prapaporn Techa-Angkoon, Yanni Sun* and Jikai Lei From 12th International Symposium on Bioinformatics Research and Applications (ISBRA) Minsk, Belarus. June 5-8, 2016 Abstract Background: Homology search is still a significant step in functional analysis for genomic data. Profile Hidden Markov Model-based homology search has been widely used in protein domain analysis in many different species. In particular, with the fast accumulation of transcriptomic data of non-model species and metagenomic data, profile homology search is widely adopted in integrated pipelines for functional analysis. While the state-of-the-art tool HMMER has achieved high sensitivity and accuracy in domain annotation, the sensitivity of HMMER on short reads declines rapidly. The low sensitivity on short read homology search can lead to inaccurate domain composition and abundance computation. Our experimental results showed that half of the reads were missed by HMMER for a RNA-Seq dataset. Thus, there is a need for better methods to improve the homology search performance for short reads. Results: We introduce a profile homology search tool named Short-Pair that is designed for short paired-end reads. By using an approximate Bayesian approach employing distribution of fragment lengths and alignment scores, Short-Pair can retrieve the missing end and determine true domains. In particular, Short-Pair increases the accuracy in aligning short reads that are part of remote homologs. We applied Short-Pair to a RNA-Seq dataset and a metagenomic dataset and quantified its sensitivity and accuracy on homology search. -

Clawhmmer: a Streaming Hmmer-Search Implementation
ClawHMMER: A Streaming HMMer-Search Implementation Daniel Reiter Horn Mike Houston Pat Hanrahan Stanford University Abstract To mitigate the problem of choosing an ad-hoc gap penalty for a given BLAST search, Krogh et al. [1994] The proliferation of biological sequence data has motivated proposed bringing the probabilistic techniques of hidden the need for an extremely fast probabilistic sequence search. Markov models(HMMs) to bear on the problem of fuzzy pro- One method for performing this search involves evaluating tein sequence matching. HMMer [Eddy 2003a] is an open the Viterbi probability of a hidden Markov model (HMM) source implementation of hidden Markov algorithms for use of a desired sequence family for each sequence in a protein with protein databases. One of the more widely used algo- database. However, one of the difficulties with current im- rithms, hmmsearch, works as follows: a user provides an plementations is the time required to search large databases. HMM modeling a desired protein family and hmmsearch Many current and upcoming architectures offering large processes each protein sequence in a large database, eval- amounts of compute power are designed with data-parallel uating the probability that the most likely path through the execution and streaming in mind. We present a streaming query HMM could generate that database protein sequence. algorithm for evaluating an HMM’s Viterbi probability and This search requires a computationally intensive procedure, refine it for the specific HMM used in biological sequence known as the Viterbi [1967; 1973] algorithm. The search search. We implement our streaming algorithm in the Brook could take hours or even days depending on the size of the language, allowing us to execute the algorithm on graphics database, query model, and the processor used. -

HMMER User's Guide
HMMER User’s Guide Biological sequence analysis using profile hidden Markov models http://hmmer.wustl.edu/ Version 2.2; August 2001 Sean Eddy Howard Hughes Medical Institute and Dept. of Genetics Washington University School of Medicine 660 South Euclid Avenue, Box 8232 Saint Louis, Missouri 63110, USA [email protected] With contributions by Ewan Birney ([email protected]) Copyright (C) 1992-2001, Washington University in St. Louis. Permission is granted to make and distribute verbatim copies of this manual provided the copyright notice and this permission notice are retained on all copies. The HMMER software package is a copyrighted work that may be freely distributed and modified under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version. Some versions of HMMER may have been obtained under specialized commercial licenses from Washington University; for details, see the files COPYING and LICENSE that came with your copy of the HMMER software. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the Appendix for a copy of the full text of the GNU General Public License. 1 Contents 1 Tutorial 6 1.1 The programs in HMMER . 6 1.2 Files used in the tutorial . 7 1.3 Searching a sequence database with a single profile HMM . 7 HMM construction with hmmbuild ............................. 7 HMM calibration with hmmcalibrate ........................... 8 Sequence database search with hmmsearch ........................ -

Swift: a GPU-Based Smith-Waterman Sequence Alignment Program
Swift: A GPU-based Smith-Waterman Sequence Alignment Program Pankaj Gupta Bioinformatics Application Developer St. Jude Children’s Research Hospital GPU Technology Conference 2012 05/15/2012 Agenda • Sequence alignment • Existing GPU-based aligners • Swift: a new GPU-based aligner • Method • Results • Problems faced • Conclusion Source: Wikipedia • Future work Sequence alignment • Sequence alignment is an important component of bioinformatics • New sequences are aligned to known sequences to • Find location of the new sequence • Find variants, insertions, and deletions • Infer functional, structural and evolutionary relationship • Example Position 0 5 10 15 20 Reference CCTTAACGTCCGTTACGTAATCG ||.|||.|||.||| Read ACTTCCTTTAGGTA Sequence alignment programs • Existing programs • BWA • BFAST • Mosaik • BLAST • Etc. • Problem with existing programs is that they are slow, less accurate, and/or require large memory • Expensive hardware is required to run these programs • Cheaper hardware is more desirable • GPUs are a good alternative GPU-based sequence aligners Features we need • Align millions of Illumina reads to the human genome • Gapped alignment • Fast • High accuracy Existing GPU-based aligners fall short Aligner Drawback Protein CUDA-BLASTP Protein sequence alignment only sequence CUDASW++ Protein sequence alignment only aligners GPU-BLAST Protein sequence alignment only GPU-HMMER Protein sequence alignment only MUMmerGPU • Exact matching • No gapped alignment MUMmerGPU++ • Exact matching • No gapped alignment DNA UGENE • Allows up to -

Hmmer and Applications
HMMER AND APPLICATIONS MVE360 – Bioinformatics 2013 Fredrik Boulund [email protected] Bioscience / Mathematical Statistics This is me • MSc Biotechnology / Mathematical statistics • PhD student Bioscience / Mathematical statistics • Research on large scale data analysis (metagenomics) • Researcher by day, musician by night • Play guitar in rock band DÖDAREN • (check us out on Spotify or come see us play sometime ;) This talk • HMMER • What it is, what are profile HMMs etc. • A brief history of [HMMER in] time • Example of an application of HMMER in metagenomics: • Finding antibiotic resistance genes in the environment What is HMMER • Sequence alignment software based on a statistical framework using profile hidden Markov models (HMM) Profile HMMs • Probabilistic models of multiple sequence alignments Alternatives • SAM (1994) (Sequence Alignment and Modeling system) • Richard Hughey • Kevin Karplus • Anders Krogh • PSI-BLAST (1997) (Position-Specific Iterative BLAST) • Stephen F. Altschul et al. (PSI-)BLAST vs HMMER BLAST HMMER • Single query sequence • Based on profile HMMs • String matching with • Higher accuracy advanced heuristics for speed • Able to detect even more remote homologs than • Mainly good for finding closely related sequences PSI-BLAST (PSI-BLAST) • Uses position-specific scoring matrices to detect more remote homologs A brief history of HMMER • Based on the principles in: • Krogh,A., Brown,M., Mian,I.S., Sjolander,K. and Haussler,D. (1994) Hidden Markov models in computational biology: Applications to protein modeling. J. Mol. Biol., 235, 1501–1531. • Durbin, Richard; Sean R. Eddy, Anders Krogh, Graeme Mitchison (1998). Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press. • Historically very slow • 100-1000 times slower than BLAST • Instrumental in the construction of: • Pfam • PROSITE • InterPro HMMER3 • Complete rewrite of HMMER2, focus on improving speed: • Eddy, S.R., 2011. -

BIMM-143: INTRODUCTION to BIOINFORMATICS (Lecture 3)
BIMM-143: INTRODUCTION TO BIOINFORMATICS (Lecture 3) Advanced Database Searching http://thegrantlab.org/bimm143/ Dr. Barry Grant Overview: Searching in databases for homologues of known proteins is a central theme in bioinformatics. The core goals are: • High sensitivity - that is, detecting even very distant relationships, and • High selectivity - namely, minimizing the number of reported ‘hits’ that are not true homologues. All database search methods involve a trade-off between sensitivity, selectivity and performance. Important questions to ask include does the method find all or most of the examples that are actually present, or does it miss a large fraction? Conversely, how many of the ‘hits’ that it reports are incorrect? Finally does the approach scale to the tractable analysis of large datasets? In this hands-on session we will explore the detection limits of conventional BLAST and introduce more sensitive (but often more time consuming) approaches including Profiles, PSI- BLAST and Hidden Markov Models (HMMs). Section 1: The limits of using BLAST for remote homologue detection Let’s return to the HBB protein that we explored in a previous class and see if we can find distantly related myoglobin and neuroglobin using this as a BLAST query. >gi|4504349|ref|NP_000509.1| hemoglobin subunit beta [Homo sapiens] MVHLTPEEKSAVTALWGKVNVDEVGGEALGRLLVVYPWTQRFFESFGDLSTPDAVMGNPKVKAHGKKVLG AFSDGLAHLDNLKGTFATLSELHCDKLHVDPENFRLLGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVAN ALAHKYH After selecting blastp and entering the sequence, be sure to change the search database to “refseq-protein” and restrict our search organism to only humans (taxid: 9605). This will help focus our results to highlight distant homologs in humans. Q1. What homologs did you find with this simple blastp search? Note their precent identities, coverage and E-values.