DOCSLIB.ORG

The Physics of Inflation 103

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Physics of Inflation 103 The Physics of Inflation A Course for Graduate Students in Particle Physics and Cosmology by Daniel Baumann Contents Preface 1 I THE QUANTUM ORIGIN OF LARGE-SCALE STRUCTURE 5 1 Classical Dynamics of Inflation7 1.1 Introduction . .7 1.2 The Horizon Problem . .8 1.2.1 FRW Spacetimes . .8 1.2.2 Causal Structure . .9 1.2.3 Shock in the CMB . 10 1.2.4 Quantum Gravity Hocus-Pocus? . 11 1.3 The Shrinking Hubble Sphere . 11 1.3.1 Solution of the Horizon Problem . 11 1.3.2 Solution of the Flatness Problem∗ ...................... 12 1.3.3 Conditions for Inflation . 13 1.4 The Physics of Inflation . 15 1.4.1 False Vacuum Inflation . 15 1.4.2 Slow-Roll Inflation . 15 1.4.3 Hybrid Inflation . 18 1.4.4 K-Inflation . 19 1.5 Outlook . 20 2 Quantum Fluctuations during Inflation 23 2.1 Motivation . 23 2.2 Classical Perturbations . 24 2.2.1 Comoving Gauge . 24 2.2.2 Constraint Equations . 25 2.2.3 Quadratic Action . 26 2.2.4 Mukhanov-Sasaki Equation . 27 2.2.5 Mode Expansion . 27 2.3 Quantum Origin of Cosmological Perturbations . 28 2.3.1 Canonical Quantization . 28 2.3.2 Non-Uniqueness of the Vacuum . 29 2.3.3 Choice of the Physical Vacuum . 30 2.3.4 Zero-Point Fluctuations in De Sitter . 32 2.4 Curvature Perturbations from Inflation . 33 2.4.1 Results for Quasi-De Sitter . 33 i ii Contents 2.4.2 Systematic Slow-Roll Expansion∗ ....................... 34 2.5 Gravitational Waves from Inflation . 36 2.6 The Lyth Bound . 37 3 Contact with Observations 39 3.1 Introduction . 39 3.2 Superhorizon (Non)-Evolution∗ ............................ 40 3.2.1 Weinberg's Proof . 40 3.2.2 Separate Universe Approach . 43 3.3 From Vacuum Fluctuations to CMB Anisotropies . 44 3.3.1 Statistics of Temperature Anisotropies . 44 3.3.2 Transfer Function and Projection Effects . 45 3.3.3 CMBSimple∗ .................................. 47 3.3.4 Coherent Phases and Superhorizon Fluctuations∗ .............. 52 3.3.5 CMB Polarization . 55 3.3.6 Non-Gaussianity . 58 3.4 From Vacuum Fluctuations to Large-Scale Structure . 59 3.4.1 Dark Matter Transfer Function . 59 3.4.2 Galaxy Biasing . 61 3.5 Future Prospects . 62 4 Reheating after Inflation 63 4.1 Introduction . 63 4.2 Elementary Theory of Reheating . 64 4.3 Parametric Resonance and Preheating . 66 4.3.1 QFT in a Time-Dependent Background . 66 4.3.2 Narrow Resonance . 67 4.3.3 Broad Resonance . 70 4.3.4 Termination of Preheating . 76 4.3.5 Gravitational Waves from Preheating . 77 4.4 Conclusions . 77 5 Primordial Non-Gaussianity 79 5.1 Why Non-Gaussianity? . 79 5.2 Gaussian and Non-Gaussian Statistics . 80 5.2.1 Statistics of CMB Anisotropies . 80 5.2.2 Sources of Non-Gaussianity . 81 5.2.3 Primordial Bispectrum . 81 5.2.4 Shapes of Non-Gaussianity . 83 5.3 Quantum Non-Gaussianities . 85 5.3.1 The in-in Formalism . 86 5.3.2 Single-Field Inflation . 90 5.4 Classical Non-Gaussianities . 99 5.4.1 The δN Formalism . 99 5.4.2 Inhomogeneous Reheating . 100 5.5 Future Prospects . 102 Contents iii II THE PHYSICS OF INFLATION 103 6 Effective Field Theory 105 6.1 Introduction . 105 6.2 Basic Principles of EFT . 106 6.2.1 Effective Actions . 106 6.2.2 Uses of EFTs . 108 6.2.3 Power Counting and Scaling . 109 6.2.4 Relevant, Irrelevant and Marginal . 110 6.2.5 Symmetries . 111 6.2.6 Quantum Corrections . 113 6.2.7 Matching and Running . 115 6.3 Seeing is Believing . 116 6.3.1 A Toy Model . 116 6.3.2 Tree-Level Matching . 116 6.3.3 Running . 118 6.3.4 One-Loop Matching . 122 6.3.5 Naturalness . 126 6.3.6 Summary . 128 6.4 The Standard Model as an Effective Theory∗ .................... 129 6.4.1 The Standard Model . 129 6.4.2 Accidental Symmetries . 131 6.4.3 Neutrino Masses . 132 6.4.4 Beyond the Standard Model Physics . 132 6.5 Conclusion . 132 7 Effective Field Theory and Inflation 133 7.1 UV Sensitivity . 133 7.2 Eta Problem . 134 7.3 Large-Field Inflation . 134 7.4 Non-Gaussianity . 135 8 Supersymmetry and Inflation 137 8.1 Introduction . 137 8.2 Facts about SUSY . 137 8.2.1 SUSY and Naturalness . 137 8.2.2 Superspace and Superfields . 139 8.2.3 Supersymmetric Lagrangians . 140 8.2.4 Miraculous Cancellations . 142 8.2.5 Non-Renormalization Theorem . 143 8.2.6 Supersymmetry Breaking . 144 8.2.7 Supergravity . 145 8.3 SUSY Inflation: Generalities . 146 8.3.1 Supergravity Eta Problem . ..
Load more

Recommended publications
  • Inflation and the Theory of Cosmological Perturbations
    Inflation and the Theory of Cosmological Perturbations A. Riotto INFN, Sezione di Padova, via Marzolo 8, I-35131, Padova, Italy. Abstract These lectures provide a pedagogical introduction to inflation and the theory of cosmological per- turbations generated during inflation which are thought to be the origin of structure in the universe. Lectures given at the: Summer School on arXiv:hep-ph/0210162v2 30 Jan 2017 Astroparticle Physics and Cosmology Trieste, 17 June - 5 July 2002 1 Notation A few words on the metric notation. We will be using the convention (−; +; +; +), even though we might switch time to time to the other option (+; −; −; −). This might happen for our convenience, but also for pedagogical reasons. Students should not be shielded too much against the phenomenon of changes of convention and notation in books and articles. Units We will adopt natural, or high energy physics, units. There is only one fundamental dimension, energy, after setting ~ = c = kb = 1, [Energy] = [Mass] = [Temperature] = [Length]−1 = [Time]−1 : The most common conversion factors and quantities we will make use of are 1 GeV−1 = 1:97 × 10−14 cm=6:59 × 10−25 sec, 1 Mpc= 3.08×1024 cm=1.56×1038 GeV−1, 19 MPl = 1:22 × 10 GeV, −1 −1 −42 H0= 100 h Km sec Mpc =2.1 h × 10 GeV, 2 −29 −3 2 4 −3 2 −47 4 ρc = 1:87h · 10 g cm = 1:05h · 10 eV cm = 8:1h × 10 GeV , −13 T0 = 2:75 K=2.3×10 GeV, 2 Teq = 5:5(Ω0h ) eV, Tls = 0:26 (T0=2:75 K) eV.
    [Show full text]
  • Baryogenesis in a CP Invariant Theory That Utilizes the Stochastic Movement of Light fields During Inflation
    Baryogenesis in a CP invariant theory Anson Hook School of Natural Sciences Institute for Advanced Study Princeton, NJ 08540 June 12, 2018 Abstract We consider baryogenesis in a model which has a CP invariant Lagrangian, CP invariant initial conditions and does not spontaneously break CP at any of the minima. We utilize the fact that tunneling processes between CP invariant minima can break CP to implement baryogenesis. CP invariance requires the presence of two tunneling processes with opposite CP breaking phases and equal probability of occurring. In order for the entire visible universe to see the same CP violating phase, we consider a model where the field doing the tunneling is the inflaton. arXiv:1508.05094v1 [hep-ph] 20 Aug 2015 1 1 Introduction The visible universe contains more matter than anti-matter [1]. The guiding principles for gener- ating this asymmetry have been Sakharov’s three conditions [2]. These three conditions are C/CP violation • Baryon number violation • Out of thermal equilibrium • Over the years, counter examples have been found for Sakharov’s conditions. One can avoid the need for number violating interactions in theories where the negative B L number is stored − in a sector decoupled from the standard model, e.g. in right handed neutrinos as in Dirac lep- togenesis [3, 4] or in dark matter [5]. The out of equilibrium condition can be avoided if one uses spontaneous baryogenesis [6], where a chemical potential is used to create a non-zero baryon number in thermal equilibrium. However, these models still require a C/CP violating phase or coupling in the Lagrangian.
    [Show full text]
  • First Year Wilkinson Microwave Anisotropy Probe (WMAP ) Observations: Determination of Cosmological Parameters
    Accepted by the Astrophysical Journal First Year Wilkinson Microwave Anisotropy Probe (WMAP ) Observations: Determination of Cosmological Parameters D. N. Spergel 2, L. Verde 2 3, H. V. Peiris 2, E. Komatsu 2, M. R. Nolta 4, C. L. Bennett 5, M. Halpern 6, G. Hinshaw 5, N. Jarosik 4, A. Kogut 5, M. Limon 5 7, S. S. Meyer 8, L. Page 4, G. S. Tucker 5 7 9, J. L. Weiland 10, E. Wollack 5, & E. L. Wright 11 [email protected] ABSTRACT WMAP precision data enables accurate testing of cosmological models. We find that the emerging standard model of cosmology, a flat ¡ −dominated universe seeded by a nearly scale-invariant adiabatic Gaussian fluctuations, fits the WMAP data. For the WMAP data 2 2 £ ¢ ¤ ¢ £ ¢ ¤ ¢ £ ¢ only, the best fit parameters are h = 0 ¢ 72 0 05, bh = 0 024 0 001, mh = 0 14 0 02, ¥ +0 ¦ 076 ¢ £ ¢ § ¢ £ ¢ = 0 ¢ 166− , n = 0 99 0 04, and = 0 9 0 1. With parameters fixed only by WMAP 0 ¦ 071 s 8 data, we can fit finer scale CMB measurements and measurements of large scale structure (galaxy surveys and the Lyman ¨ forest). This simple model is also consistent with a host of other astronomical measurements: its inferred age of the universe is consistent with stel- lar ages, the baryon/photon ratio is consistent with measurements of the [D]/[H] ratio, and the inferred Hubble constant is consistent with local observations of the expansion rate. We then fit the model parameters to a combination of WMAP data with other finer scale CMB experi- ments (ACBAR and CBI), 2dFGRS measurements and Lyman ¨ forest data to find the model’s 1WMAP is the result of a partnership between Princeton University and NASA's Goddard Space Flight Center.
    [Show full text]
  • Arxiv:Hep-Ph/9912247V1 6 Dec 1999 MGNTV COSMOLOGY IMAGINATIVE Abstract
    IMAGINATIVE COSMOLOGY ROBERT H. BRANDENBERGER Physics Department, Brown University Providence, RI, 02912, USA AND JOAO˜ MAGUEIJO Theoretical Physics, The Blackett Laboratory, Imperial College Prince Consort Road, London SW7 2BZ, UK Abstract. We review1 a few off-the-beaten-track ideas in cosmology. They solve a variety of fundamental problems; also they are fun. We start with a description of non-singular dilaton cosmology. In these scenarios gravity is modified so that the Universe does not have a singular birth. We then present a variety of ideas mixing string theory and cosmology. These solve the cosmological problems usually solved by inflation, and furthermore shed light upon the issue of the number of dimensions of our Universe. We finally review several aspects of the varying speed of light theory. We show how the horizon, flatness, and cosmological constant problems may be solved in this scenario. We finally present a possible experimental test for a realization of this theory: a test in which the Supernovae results are to be combined with recent evidence for redshift dependence in the fine structure constant. arXiv:hep-ph/9912247v1 6 Dec 1999 1. Introduction In spite of their unprecedented success at providing causal theories for the origin of structure, our current models of the very early Universe, in partic- ular models of inflation and cosmic defect theories, leave several important issues unresolved and face crucial problems (see [1] for a more detailed dis- cussion). The purpose of this chapter is to present some imaginative and 1Brown preprint BROWN-HET-1198, invited lectures at the International School on Cosmology, Kish Island, Iran, Jan.
    [Show full text]
  • Inflation Without Quantum Gravity
    Inflation without quantum gravity Tommi Markkanen, Syksy R¨as¨anen and Pyry Wahlman University of Helsinki, Department of Physics and Helsinki Institute of Physics P.O. Box 64, FIN-00014 University of Helsinki, Finland E-mail: tommi dot markkanen at helsinki dot fi, syksy dot rasanen at iki dot fi, pyry dot wahlman at helsinki dot fi Abstract. It is sometimes argued that observation of tensor modes from inflation would provide the first evidence for quantum gravity. However, in the usual inflationary formalism, also the scalar modes involve quantised metric perturbations. We consider the issue in a semiclassical setup in which only matter is quantised, and spacetime is classical. We assume that the state collapses on a spacelike hypersurface, and find that the spectrum of scalar perturbations depends on the hypersurface. For reasonable choices, we can recover the usual inflationary predictions for scalar perturbations in minimally coupled single-field models. In models where non-minimal coupling to gravity is important and the field value is sub-Planckian, we do not get a nearly scale-invariant spectrum of scalar perturbations. As gravitational waves are only produced at second order, the tensor-to-scalar ratio is negligible. We conclude that detection of inflationary gravitational waves would indeed be needed to have observational evidence of quantisation of gravity. arXiv:1407.4691v2 [astro-ph.CO] 4 May 2015 Contents 1 Introduction 1 2 Semiclassical inflation 3 2.1 Action and equations of motion 3 2.2 From homogeneity and isotropy to perturbations 6 3 Matching across the collapse 7 3.1 Hypersurface of collapse 7 3.2 Inflation models 10 4 Conclusions 13 1 Introduction Inflation and the quantisation of gravity.
    [Show full text]
  • FIRST-YEAR WILKINSON MICROWAVE ANISOTROPY PROBE (WMAP) 1 OBSERVATIONS: DETERMINATION of COSMOLOGICAL PARAMETERS D. N. Spergel,2
    The Astrophysical Journal Supplement Series, 148:175–194, 2003 September E # 2003. The American Astronomical Society. All rights reserved. Printed in U.S.A. FIRST-YEAR WILKINSON MICROWAVE ANISOTROPY PROBE (WMAP)1 OBSERVATIONS: DETERMINATION OF COSMOLOGICAL PARAMETERS D. N. Spergel,2 L. Verde,2,3 H. V. Peiris,2 E. Komatsu,2 M. R. Nolta,4 C. L. Bennett,5 M. Halpern,6 G. Hinshaw,5 N. Jarosik,4 A. Kogut,5 M. Limon,5,7 S. S. Meyer,8 L. Page,4 G. S. Tucker,5,7,9 J. L. Weiland,10 E. Wollack,5 and E. L. Wright11 Received 2003 February 11; accepted 2003 May 20 ABSTRACT WMAP precision data enable accurate testing of cosmological models. We find that the emerging standard model of cosmology, a flat Ã-dominated universe seeded by a nearly scale-invariant adiabatic Gaussian fluctuations, fits the WMAP data. For the WMAP data only, the best-fit parameters are h ¼ 0:72 Æ 0:05, 2 2 þ0:076 bh ¼ 0:024 Æ 0:001, mh ¼ 0:14 Æ 0:02, ¼ 0:166À0:071, ns ¼ 0:99 Æ 0:04, and 8 ¼ 0:9 Æ 0:1. With parameters fixed only by WMAP data, we can fit finer scale cosmic microwave background (CMB) measure- ments and measurements of large-scale structure (galaxy surveys and the Ly forest). This simple model is also consistent with a host of other astronomical measurements: its inferred age of the universe is consistent with stellar ages, the baryon/photon ratio is consistent with measurements of the [D/H] ratio, and the inferred Hubble constant is consistent with local observations of the expansion rate.
    [Show full text]
  • Inflationary Cosmology: from Theory to Observations
    Inflationary Cosmology: From Theory to Observations J. Alberto V´azquez1, 2, Luis, E. Padilla2, and Tonatiuh Matos2 1Instituto de Ciencias F´ısicas,Universidad Nacional Aut´onomade Mexico, Apdo. Postal 48-3, 62251 Cuernavaca, Morelos, M´exico. 2Departamento de F´ısica,Centro de Investigaci´ony de Estudios Avanzados del IPN, M´exico. February 10, 2020 Abstract The main aim of this paper is to provide a qualitative introduction to the cosmological inflation theory and its relationship with current cosmological observations. The inflationary model solves many of the fundamental problems that challenge the Standard Big Bang cosmology, such as the Flatness, Horizon, and the magnetic Monopole problems. Additionally, it provides an explanation for the initial conditions observed throughout the Large-Scale Structure of the Universe, such as galaxies. In this review, we describe general solutions to the problems in the Big Bang cosmology carry out by a single scalar field. Then, with the use of current surveys, we show the constraints imposed on the inflationary parameters (ns; r), which allow us to make the connection between theoretical and observational cosmology. In this way, with the latest results, it is possible to select, or at least to constrain, the right inflationary model, parameterized by a single scalar field potential V (φ). Abstract El objetivo principal de este art´ıculoes ofrecer una introducci´oncualitativa a la teor´ıade la inflaci´onc´osmica y su relaci´oncon observaciones actuales. El modelo inflacionario resuelve algunos problemas fundamentales que desaf´ıanal modelo est´andarcosmol´ogico,denominado modelo del Big Bang caliente, como el problema de la Planicidad, el Horizonte y la inexistencia de Monopolos magn´eticos.Adicionalmente, provee una explicaci´onal origen de la estructura a gran escala del Universo, como son las galaxias.
    [Show full text]
  • Who Is the Inflaton ?
    View metadata, citation and similar papers at core.ac.uk Who is the Inflaton ? brought to you by CORE provided by CERN Document Server R. Brout Service de Physique Th´eorique, Universit´e Libre de Bruxelles, CP 225, Bvd. du Triomphe, B-1050 Bruxelles, Belgium, (email: [email protected]). It is proposed that the inflaton field is proportional to the fluctuation of the number density of degrees of freedom of the fields of particle physics. These possess cut-off momenta at O (mP lanck), but this fluctuates since the fields propagate in an underlying space-time transplanckian substratum. If the latter is modeled as an instanton fluid in the manner of Hawking's space-time foam, then this identification, in the rough, is equivalent to the inflaton being the fluctuation of the spatial density of instantons. This interpretation is suggested by Volovik's analogy between space-time and the superfluid. (However, unlike for the latter, one cannot argue from the analogy that the cosmological constant vanishes). In our interpretation Linde's phenomenology of inflation takes on added luster in this way to look at things, since inflation and particle production follow quite naturally from familiar physical concepts operating on a "cisplanckian" level. I. INTRODUCTION In his lectures on cosmology at Erice 1999, Professor E. Kolb in extolling the virtues of the inflaton scenario of inflation closed his inspiring lesson with the resounding question : "Who is the inflaton ?" In the foregoing I shall hazard an answer. My intention, in the present paper, is to introduce more a theoretical framework of conjectural character than any quantitative realization.
    [Show full text]
  • Evolution of the Cosmological Horizons in a Concordance Universe
    Evolution of the Cosmological Horizons in a Concordance Universe Berta Margalef–Bentabol 1 Juan Margalef–Bentabol 2;3 Jordi Cepa 1;4 [email protected] [email protected] [email protected] 1Departamento de Astrofísica, Universidad de la Laguna, E-38205 La Laguna, Tenerife, Spain: 2Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, E-28040 Madrid, Spain. 3Facultad de Ciencias Físicas, Universidad Complutense de Madrid, E-28040 Madrid, Spain. 4Instituto de Astrofísica de Canarias, E-38205 La Laguna, Tenerife, Spain. Abstract The particle and event horizons are widely known and studied concepts, but the study of their properties, in particular their evolution, have only been done so far considering a single state equation in a deceler- ating universe. This paper is the first of two where we study this problem from a general point of view. Specifically, this paper is devoted to the study of the evolution of these cosmological horizons in an accel- erated universe with two state equations, cosmological constant and dust. We have obtained closed-form expressions for the horizons, which have allowed us to compute their velocities in terms of their respective recession velocities that generalize the previous results for one state equation only. With the equations of state considered, it is proved that both velocities remain always positive. Keywords: Physics of the early universe – Dark energy theory – Cosmological simulations This is an author-created, un-copyedited version of an article accepted for publication in Journal of Cosmology and Astroparticle Physics. IOP Publishing Ltd/SISSA Medialab srl is not responsible for any errors or omissions in this version of the manuscript or any version derived from it.
    [Show full text]
  • CMBEASY:: an Object Oriented Code for the Cosmic Microwave
    www.cmbeasy.org CMBEASY:: an Object Oriented Code for the Cosmic Microwave Background Michael Doran∗ Department of Physics & Astronomy, HB 6127 Wilder Laboratory, Dartmouth College, Hanover, NH 03755, USA and Institut f¨ur Theoretische Physik der Universit¨at Heidelberg, Philosophenweg 16, 69120 Heidelberg, Germany We have ported the cmbfast package to the C++ programming language to produce cmbeasy, an object oriented code for the cosmic microwave background. The code is available at www.cmbeasy.org. We sketch the design of the new code, emphasizing the benefits of object orienta- tion in cosmology, which allow for simple substitution of different cosmological models and gauges. Both gauge invariant perturbations and quintessence support has been added to the code. For ease of use, as well as for instruction, a graphical user interface is available. I. INTRODUCTION energy, dark matter, baryons and neutrinos. The dark energy can be a cosmological constant or quintessence. The cmbfast computer program for calculating cos- There are three scalar field field models implemented, or mic microwave background (CMB) temperature and po- alternatively one may specify an equation-of-state his- larization anisotropy spectra, implementing the fast line- tory. Furthermore, the modular code is easily adapted of-sight integration method, has been publicly available to new problems in cosmology. since 1996 [1]. It has been widely used to calculate spec- In the next section IIA we explain object oriented pro- cm- tra for open, closed, and flat cosmological models con- gramming and its use in cosmology. The design of beasy taining baryons and photons, cold dark matter, massless is presented in section II B, while the graphical and massive neutrinos, and a cosmological constant.
    [Show full text]
  • Supersymmetry and Inflation
    Supersymmetry and Inflation Sergio FERRARA (CERN – LNF INFN) July 14 , 2015 Fourteenth Marcel Grossmann Meeting, MG14 University of Rome “La Sapienza”, July 12-18 2015 S. Ferrara - MG14, U. Rome "La Sapienza" 1 July 2015 Contents 1. Single field inflation and Supergravity embedding 2. Inflation and Supersymmetry breaking 3. Minimal models for inflation: a. One chiral multiplet (sgoldstino inflation) b. Two chiral multiplets: T (inflaton), S (sgoldstino) 4. R + R2 Supergravity 5. Nilpotent inflation (sgoldstino-less models) 6. Models with two Supersymmetry breaking scales S. Ferrara - MG14, U. Rome "La Sapienza" July 2015 2 We describe approaches to inflaton dynamics based on Supergravity, the combination of Supersymmetry with General Relativity (GR). Nowadays it is well established that inflationary Cosmology is accurately explained studying the evolution of a single real scalar field, the inflaton, in a Friedmann, Lemaître, Robertson, Walker geometry. A fundamental scalar field, which described the Higgs particle, was also recently discovered at LHC, confirming the interpretation of the Standard Model as a spontaneously broken phase (BEH mechanism) of a non-abelian Yang-Mills theory (Brout, Englert, Higgs, 1964). S. Ferrara - MG14, U. Rome "La Sapienza" July 2015 3 There is then some evidence that Nature is inclined to favor, both in Cosmology and in Particle Physics, theories which use scalar degrees of freedom, even if in diverse ranges of energy scales. Interestingly, there is a cosmological model where the two degrees of freedom, inflaton and Higgs, are identified, the Higgs inflation model (Bezrukov, Shaposhnikov, 2008), where a non-minimal coupling 2 h R of the Higgs field h to gravity is introduced.
    [Show full text]
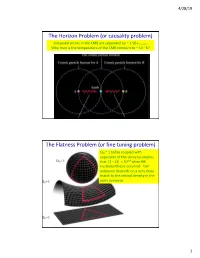
  • Or Causality Problem) the Flatness Problem (Or Fine Tuning Problem
    4/28/19 The Horizon Problem (or causality problem) Antipodal points in the CMB are separated by ~ 1.96 rhorizon. Why then is the temperature of the CMB constant to ~ 10-5 K? The Flatness Problem (or fine tuning problem) W0 ~ 1 today coupled with expansion of the Universe implies that |1 – W| < 10-14 when BB nucleosynthesis occurred. Our existence depends on a very close match to the critical density in the early Universe 1 4/28/19 Theory of Cosmic Inflation Universe undergoes brief period of exponential expansion How Inflation Solves the Flatness Problem 2 4/28/19 Cosmic Inflation Summary Standard Big Bang theory has problems with tuning and causality Inflation (exponential expansion) solves these problems: - Causality solved by observable Universe having grown rapidly from a small region that was in causal contact before inflation - Fine tuning problems solved by the diluting effect of inflation Inflation naturally explains origin of large scale structure: - Early Universe has quantum fluctuations both in space-time itself and in the density of fields in space. Inflation expands these fluctuation in size, moving them out of causal contact with each other. Thus, large scale anisotropies are “frozen in” from which structure can form. Some kind of inflation appears to be required but the exact inflationary model not decided yet… 3 4/28/19 BAO: Baryonic Acoustic Oscillations Predict an overdensity in baryons (traced by galaxies) ~ 150 Mpc at the scale set by the distance that the baryon-photon acoustic wave could have traveled before CMB recombination 4 4/28/19 Curves are different models of Wm A measure of clustering of SDSS Galaxies of clustering A measure Eisenstein et al.
    [Show full text]