Fine and Hyperfine Splitting of the Low-Lying States of $^ 9$ Be
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Marginalized Kernels Between Labeled Graphs
Marginalized Kernels Between Labeled Graphs Hisashi Kashima [email protected] IBM Tokyo Research Laboratory, 1623-14 Shimotsuruma, Yamato-shi, 242-8502 Kanagawa, Japan Koji Tsuda [email protected] Max Planck Institute for Biological Cybernetics, Spemannstr. 38, 72076 T¨ubingen,Germany; and AIST Computational Biology Research Center, 2-43 Aomi, Koto-ku, 135-0064 Tokyo, Japan Akihiro Inokuchi [email protected] IBM Tokyo Research Laboratory, 1623-14 Shimotsuruma, Yamato-shi, 242-8502 Kanagawa, Japan Abstract of drugs from their chemical structures (Kramer & De Raedt, 2001; Inokuchi et al., 2000). A new kernel function between two labeled graphs is presented. Feature vectors are de- Kernel methods such as support vector machines are fined as the counts of label paths produced becoming increasingly popular for their high perfor- by random walks on graphs. The kernel com- mance (Sch¨olkopf & Smola, 2002). In kernel meth- putation finally boils down to obtaining the ods, all computations are done via a kernel function, stationary state of a discrete-time linear sys- which is the inner product of two vectors in a fea- tem, thus is efficiently performed by solv- ture space. In order to apply kernel methods to graph ing simultaneous linear equations. Our ker- classification, we first need to define a kernel func- nel is based on an infinite dimensional fea- tion between the graphs. However, defining a ker- ture space, so it is fundamentally different nel function is not an easy task, because it must be from other string or tree kernels based on dy- designed to be positive semidefinite2. -

American Primacy and the Global Media
City Research Online City, University of London Institutional Repository Citation: Chalaby, J. (2009). Broadcasting in a Post-National Environment: The Rise of Transnational TV Groups. Critical Studies in Television, 4(1), pp. 39-64. doi: 10.7227/CST.4.1.5 This is the accepted version of the paper. This version of the publication may differ from the final published version. Permanent repository link: https://openaccess.city.ac.uk/id/eprint/4508/ Link to published version: http://dx.doi.org/10.7227/CST.4.1.5 Copyright: City Research Online aims to make research outputs of City, University of London available to a wider audience. Copyright and Moral Rights remain with the author(s) and/or copyright holders. URLs from City Research Online may be freely distributed and linked to. Reuse: Copies of full items can be used for personal research or study, educational, or not-for-profit purposes without prior permission or charge. Provided that the authors, title and full bibliographic details are credited, a hyperlink and/or URL is given for the original metadata page and the content is not changed in any way. City Research Online: http://openaccess.city.ac.uk/ [email protected] Broadcasting in a post-national environment: The rise of transnational TV groups Author: Dr Jean K. Chalaby Department of Sociology City University Northampton Square London EC1V 0HB Tel: 020 7040 0151 Fax: 020 7040 8558 Email: [email protected] Jean K. Chalaby is Reader in the Department of Sociology, City University in London. He is the author of The Invention of Journalism (1998), The de Gaulle Presidency and the Media (2002) and Transnational Television in Europe: Reconfiguring Global Communications Networks (2009). -

City of Rio Rancho, New Mexico July 2021 Single Family Residential Starts by Permit Issue Date
CITY OF RIO RANCHO, NEW MEXICO JULY 2021 SINGLE FAMILY RESIDENTIAL STARTS BY PERMIT ISSUE DATE ADDRESS LEGAL DESCRIPTION PERMIT CONTRACTOR LAND USE PERMIT ISSUE Application Street Permit Permit SQUARE PERMIT DATE ZONE Type number Street Name Suffix Quadrant Unit Block Lot Year Number Status FOOTAGE VALUATION TYPE YYMMDD DISTRICT ACREAGE MAR2 5418 BLUE GRAMA DR NE TM 1 1 21 8291 AP 3,592 $241,418 BLDG 210722 MTV ENTERPRISES, LLC MU-A 0.1707 MAR2 2811 KINGS CANYON LP NE RDOM 86 21 8545 AP 2,632 $176,897 BLDG 210728 PULTE DEVELOPMENT NEW MEXICO, R-4 0.1524 35N 5739 COSMO PL NE 35N 1 17 21 3615 AP 2,082 $139,931 BLDG 210702 TQM, LLC R-3 0.1523 35N 5769 COSMO CT NE 35N 1 21 21 7722 AP 1,985 $133,412 BLDG 210719 TQM, LLC R-3 0.1523 BMH1 3101 ALLYSON WY NE BMH1 1 5 21 8930 AP 3,507 $235,705 BLDG 210728 PULTE DEVELOPMENT NEW MEXICO, R-4 0.2733 BMH1 3017 SHANNON LN NE BMH1 2 20 21 8941 PC 3,090 $207,679 BLDG 210730 PULTE DEVELOPMENT NEW MEXICO, R-4 0.1241 HS28 4505 BALD EAGLE LP NE HS28 13 18 21 7019 AP 2,751 $184,895 BLDG 210723 HAKES BROTHERS CONSTRUCTION, L SU/SF 0.1964 HS28 4509 BALD EAGLE LP NE HS28 13 19 21 6954 AP 2,464 $165,605 BLDG 210723 HAKES BROTHERS CONSTRUCTION, L SU/SF 0.145 HS28 4513 BALD EAGLE LP NE HS28 13 20 21 7018 AP 2,464 $165,605 BLDG 210723 HAKES BROTHERS CONSTRUCTION, L SU/SF 0.145 HS28 4517 BALD EAGLE LP NE HS28 13 21 21 6951 AP 2,284 $153,508 BLDG 210723 HAKES BROTHERS CONSTRUCTION, L SU/SF 0.145 HS28 4521 BALD EAGLE LP NE HS28 13 22 21 7023 AP 2,751 $184,895 BLDG 210723 HAKES BROTHERS CONSTRUCTION, L SU/SF 0.1415 HS28 -

Isthmus CHICAGO, Juno 22
8UOAR ilfi A WEATHER Cuio: 3.60c por lb., $77:20 Thor., mln., 74. por ton, liar., 8 a. m., S0.0S. Ucota, 11b. Co', por cwt., Rain, 24h, a. m., tnth 188.60 por ton. Star Wind, 12m., MB, .jjj Telephone 2365 Star RmnriPM office The Largest Daily Paper in The Territory SECOND EDITION. vol. xx TWENTY PAQES. HONOLULU. HAWAII. S. rURDAY, JUNK 22, VH2. TWENTY PAGES, - THE TAFT PLATFORM ADOPTED 1 (Associated Press Cable to the Star.) j he Isthmus CHICAGO, Juno 22. The vote on ihe nooption of r the Taft platform was 6C6 ayes, 53 noes, absent 10. Three hundred and forty-thre- e delegates fol- lowing the Roosevelt lead refused to vote, Inc uding twenty-fou- r California "My visit to the Hawaiian Islands things. delegates. The entire delegation of Maine, Nebraska, South Dakota and is entirely duo to tho "I was in Culebra cut when a land' enthusiastic Miflsourl solidly aye." Illinois voted forty-si- x aye, nine not voting; Ohio boosting of Major Winslow tho slide occurred. These slides of are not voted fourteen nyo, thirty-fou- r not v ting; Massachusetts twenty aye, four- army, formerly stationed here," said as you would suppose from tho out- teen not voting. tJoorgo B. Thayer, a lawyer of Hart- side,- but arc caused by the hills on California Declines to Vote. ford, Conn., this morning. Mr. Thayer, tho sides of the cut settling, causing When California was called Meyer Lissner of Lai Angeles, chairman of 60 years jaunti- up. although old, walked the arth in tho cut to buck tho delegation announced that California declined to vote and a storm of ly across the Isthmus of Panama on "The men were at their noon lunch applause fo'.lowed. -
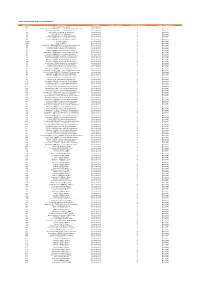
Codes Used in D&M
CODES USED IN D&M - MCPS A DISTRIBUTIONS D&M Code D&M Name Category Further details Source Type Code Source Type Name Z98 UK/Ireland Commercial International 2 20 South African (SAMRO) General & Broadcasting (TV only) International 3 Overseas 21 Australian (APRA) General & Broadcasting International 3 Overseas 36 USA (BMI) General & Broadcasting International 3 Overseas 38 USA (SESAC) Broadcasting International 3 Overseas 39 USA (ASCAP) General & Broadcasting International 3 Overseas 47 Japanese (JASRAC) General & Broadcasting International 3 Overseas 48 Israeli (ACUM) General & Broadcasting International 3 Overseas 048M Norway (NCB) International 3 Overseas 049M Algeria (ONDA) International 3 Overseas 58 Bulgarian (MUSICAUTOR) General & Broadcasting International 3 Overseas 62 Russian (RAO) General & Broadcasting International 3 Overseas 74 Austrian (AKM) General & Broadcasting International 3 Overseas 75 Belgian (SABAM) General & Broadcasting International 3 Overseas 79 Hungarian (ARTISJUS) General & Broadcasting International 3 Overseas 80 Danish (KODA) General & Broadcasting International 3 Overseas 81 Netherlands (BUMA) General & Broadcasting International 3 Overseas 83 Finnish (TEOSTO) General & Broadcasting International 3 Overseas 84 French (SACEM) General & Broadcasting International 3 Overseas 85 German (GEMA) General & Broadcasting International 3 Overseas 86 Hong Kong (CASH) General & Broadcasting International 3 Overseas 87 Italian (SIAE) General & Broadcasting International 3 Overseas 88 Mexican (SACM) General & Broadcasting -

Ep 2681242 B1
(19) TZZ _ _T (11) EP 2 681 242 B1 (12) EUROPEAN PATENT SPECIFICATION (45) Date of publication and mention (51) Int Cl.: of the grant of the patent: C07K 16/18 (2006.01) A61K 39/00 (2006.01) 24.01.2018 Bulletin 2018/04 C07K 16/22 (2006.01) (21) Application number: 12708472.1 (86) International application number: PCT/US2012/027154 (22) Date of filing: 29.02.2012 (87) International publication number: WO 2012/118903 (07.09.2012 Gazette 2012/36) (54) SCLEROSTIN AND DKK-1 BISPECIFIC BINDING AGENTS SCLEROSTIN- UND DKK-1-BISPEZIFISCHE BINDEMITTEL AGENTS LIANTS BISPÉCIFIQUEMENT SCLÉROSTINE ET DKK-1 (84) Designated Contracting States: (74) Representative: J A Kemp AL AT BE BG CH CY CZ DE DK EE ES FI FR GB 14 South Square GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO Gray’s Inn PL PT RO RS SE SI SK SM TR London WC1R 5JJ (GB) Designated Extension States: BA ME (56) References cited: WO-A1-2009/047356 WO-A2-2006/015373 (30) Priority: 01.03.2011 US 201161448089 P WO-A2-2006/119062 WO-A2-2009/149189 05.05.2011 US 201161482979 P WO-A2-2012/058393 (43) Date of publication of application: • HOLT L J ET AL: "Domain antibodies: proteins 08.01.2014 Bulletin 2014/02 for therapy", TRENDS IN BIOTECHNOLOGY, ELSEVIER PUBLICATIONS, CAMBRIDGE, GB, (73) Proprietor: Amgen Inc. vol. 21, no. 11, 1 November 2003 (2003-11-01), Thousand Oaks, California 91320-1799 (US) pages 484-490, XP004467495, ISSN: 0167-7799, DOI: 10.1016/J.TIBTECH.2003.08.007 (72) Inventors: • DAVIES J ET AL: "Affinity improvement of single • FLORIO, Monica antibody VH domains: residues in all three Thousand Oaks, CA 91362 (US) hypervariable regions affect antigen binding", • ARORA, Taruna IMMUNOTECHNOLOGY, ELSEVIER SCIENCE Thousand Oaks, CA 91320 (US) PUBLISHERS BV, NL, vol. -

Securities and Exchange Commission Form 10-K Viacom
SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 10-K ANNUAL REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the fiscal year ended December 31, 2003 OR o TRANSITION REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the transition period from to Commission File Number 001-09553 VIACOM INC. (Exact Name Of Registrant As Specified In Its Charter) DELAWARE 04-2949533 (State or Other Jurisdiction of (I.R.S. Employer Incorporation Or Organization) Identification Number) 1515 Broadway New York, NY 10036 (212) 258-6000 (Address, including zip code, and telephone number, including area code, of registrant's principal executive offices) Securities Registered Pursuant to Section 12(b) of the Act: Name of Each Exchange on Title of Each Class Which Registered Class A Common Stock, $0.01 par value New York Stock Exchange Class B Common Stock, $0.01 par value New York Stock Exchange 7.75% Senior Notes due 2005 American Stock Exchange 7.625% Senior Debentures due 2016 American Stock Exchange 7.25% Senior Notes due 2051 New York Stock Exchange Securities Registered Pursuant to Section 12(g) of the Act: None (Title Of Class) Indicate by check mark whether the registrant (1) has filed all reports required to be filed by Section 13 or 15(d) of the Securities Exchange Act of 1934 during the preceding 12 months (or for such shorter period that the registrant was required to file such reports), and (2) has been subject to such filing requirements for the past 90 days. -

The Case for Export a Collection of Case Studies About Exporting Design
The Case for exporT A collection of case studies about exporting design. The Case for exporT A collection of case studies about exporting design. Disclaimer This information guide is designed to help you better understand the issues associated with export. You should not regard this publication as an authoritative statement on relevant laws, fees or procedures. You should also note that the requirements and fees may change from time to time. Every effort has been made to ensure the information presented is accurate, however no liability is accepted for any inclusions or advice given or for omissions from the publication. © 2009 State of Victoria. No part may be reproduced by any process except in accordance with the provisions of the Copyright Act 1968. MinisTer’s Director’s MESSAGe MESSAGe The Victorian Government Our access to export markets is constantly Exporting design, whether Navigate your way through The Case for Export being improved through tariff reductions, and learn some of the skills required to export is proud to support The new Free Trade Agreements and improvements services or products, is design services. What research is required? Case for Export, inspiring in technologies. The Brumby Government like taking a journey into What should be included in a fact finding has set an overall export target of $35 billion mission? Is it possible to communicate with Victorian designers to take by 2015 and has recently boosted support with the unknown. clients from Australia? Once an overseas their design services to the a number of new measures including a $24.8 Some designers find the process to be a roller commission is obtained, does it require a rest of the world. -

And IL-7Tg Mice. Spleen Cells Were Pr
IgH from sequences. aspercent one million usage wascalculated segment orientation with respect to the in D C57BL/6J mice informat methods sorted and subjected to mouse surface IgH CD19, B220, and gene IgM. One expression to two analysis million B as cells and (CD19 young descr IL Spleen cells were prepared from a Supplemental Figure 1 SUPPLEMENTAL INFORMATION % VH sement usage % VH sement usage % VH sement usage 10.0 10.0 10.0 0.0 0.5 1.0 0.0 0.5 1.0 2.0 4.0 6.0 8.0 2.0 4.0 6.0 8.0 0.0 0.5 1.0 2.0 4.0 6.0 8.0 5’ . VH1-85 VH1-85 VH1-85 ion system VH1-84 VH1-84 VH1-84 VH1-82 VH1-82 VH1-82 We used C57BL/6 V VH1-81 VH1-81 VH1-81 VH1-80 VH1-80 VH1-80 VH1-78 VH1-78 VH1-78 VH1-77 VH1-77 VH1-77 Adult wildtype Adult Young wildtype Young Young IL-7Tg Young Adult IL-7 Adult Young wildtype Young VH1-76 VH1-76 VH1-76 wildtype Adult VHgenesdistal to DH-JH VH1-75 VH1-75 VH1-75 VH1-74 VH1-74 VH1-74 - VH1-72 VH1-72 VH1-72 7Tg (n=5) mice and stained with a cocktail of fluorescent antibodies specific for VH1-71 VH1-71 VH1-71 VH8-12 VH8-12 VH8-12 VH1-69 VH1-69 VH1-69 VH1-67 VH1-67 VH1-67 VH1-66 VH1-66 VH1-66 VH8-11 VH8-11 VH8-11 VH1-64 VH1-64 VH1-64 VH1-63 VH1-63 -/- VH1-63 VH1-62-3 VH1-62-3 VH1-62-3 ® VH1-62-2 VH1-62-2 VH1-62-2 VH1-62-1 VH1-62-1 VH1-62-1 were VH 1-61 VH 1-61 VH 1-61 (I VH1-59 VH1-59 VH1-59 VH1-58 VH1-58 VH1-58 VH8-8 VH8-8 VH8-8 MGT VH1-56 VH1-56 VH1-56 VH1-55 VH1-55 VH1-55 . -

The Essentials
COMING SOON The Essentials New channel numbers Vanity Fair on Sky Movies 2 Now Sky is even Your cut-out-and-keep guide (channel 302) Entertainment 155 E! 264 DiscHome&H 408 Sky Spts News Kids 101 BBC1 157 Ftn 265 Disc H&H +1 410 Eurosport UK 601 Cartoon Netwrk 102 BBC2 159 OBE 267 Artsworld 411 Eurosport2 UK 602 Cartoon Nwk + easier to use! 103 ITV1 161 Biography 269 UKTV Br’t Ideas 413 Motors TV 603 Boomerang 104 Channel 4 / 163 Hollywood TV 271 Performance 415 At The Races 604 Nickelodeon S4C 165 Bonanza 273 Fashion TV 417 NASN 605 Nick Replay We’re improving the way your on-screen TV guide 105 five 169 UKTVG2+1 275 Majestic TV 419 Extreme Sports 606 Nicktoons works, making it simpler and smoother than ever. If the 106 Sky One 173 Open Access 2 277 LONDON TV 421 Chelsea TV 607 Trouble 107 Sky Two 179 FX 279 Real Estate TV 423 Golf Channel 608 Trouble Reload changes haven’t happened on your screen yet, don’t 108 Sky Three 180 FX+ 281 Wine TV 425 Channel 425 609 Jetix worry, they will very soon! Read all about them here 109 UKTV Gold 181 Information TV 283 Disc. T&L 427 TWC 110 UKTV Gold +1 183 Passion TV 285 Baby Channel 429 Setanta Sports1 111 UKTVG2 185 abc1 430 Setanta Sports2 112 LIVINGtv 187 Raj TV Movies 432 Racing UK 113 LIVINGtv +1 189 More4 +1 301 Sky Movies 1 434 Setanta Ireland 114 LIVINGtv2 193 Rapture TV 302 Sky Movies 2 436 Celtic TV Sky Guide changes 115 BBC THREE 195 propeller 303 Sky Movies 3 438 Rangers TV 116 BBC FOUR 971 BBC 1 Scotland 304 Sky Movies 4 440 Sport Nation 972 BBC 1 Wales 305 Sky Movies 5 480 Prem Plus -

Conditioning Prices on Purchase History
Conditioning Prices on Purchase History Alessandro Acquisti Hal R. Varian [email protected] University of California, Berkeley Conditioning Prices – p.1/34 Introduction • 1988: cost of a gigabyte of hard disk storage was about $11,500 • 2000: cost was $13, roughly 900 times cheaper. • It is now possible to save, analyze, and use information about individual customers. • Loyalty programs for airlines, hotels, supermarkets. • Cookies, logins, credit card numbers for online purchases. • But buyers can take defensive measures. • How do these effects work themselves out? Conditioning Prices – p.2/34 Example of Netscape cookies .yahoo.com TRUE / FALSE 2060279446 B 99uerc0teitt0&b=2 .yahoo.com TRUE / FALSE 1271361534 Y v=1&n=9p40tt0kndtpl&l=7l0h80d/o&p=m1f2sg02010205 www.weather.com FALSE / FALSE 1006221546 footprint 1%7Chomegarden_garden .amazon.com TRUE / FALSE 1011859195 session-id 104-4960085-2200764 .amazon.com TRUE / FALSE 1011859195 session-id-time 1011859200 Wed%20Oct%2024%2015:40:02%20EDT%202001%200.1921455979 Conditioning Prices – p.3/34 The model • One profit-maximizing seller with zero MC. • Two-periods; seller can commit to price plan. • Seller has way to remember behavior of customers, e.g., cookies. • Consumers want at most one unit per period. • Two types of consumers with wtp vH and vL, with fraction π having high value. • Consumer indifference resolved in favor of seller. Conditioning Prices – p.4/34 Pricing strategy • Flat pricing • Sell only to high, makes profit 2πvH . • Sell to all, makes profit 2vL. • Price conditioning: an example • Set high price first period • Sell at high price second period to those who bought first period • Sell at low price to others second period. -

The Human Immunoglobulin VH Gene Repertoire Is Genetically Controlled and Unaltered by Chronic Autoimmune Stimulation
The Human Immunoglobulin VH Gene Repertoire is Genetically Controlled and Unaltered by Chronic Autoimmune Stimulation Hitoshi Kohsaka,* Dennis A. Carson,§ Laura Z. Rassenti,§ William E.R. Ollier,ʈ Pojen P. Chen,§ Thomas J. Kipps,§ and Nobuyuki Miyasaka‡ *Division of Immunological Diseases, Medical Research Institute, and ‡First Department of Internal Medicine, Tokyo Medical and Dental University, Tokyo, 113, Japan; §Department of Medicine, Sam and Rose Stein Institute for Research on Aging, University of California, San Diego, La Jolla, California 92093; and ʈARC Epidemiology Research Unit, University of Manchester, Manchester, M13 9PT, United Kingdom Abstract consists of 22 functional genes. The VH1 and VH4 families each contain approximately a dozen functional genes, and VH2, The factors controlling immunoglobulin (Ig) gene repertoire VH5, VH6, and VH7 families contain 3, 2, 1, and 1 functional formation are poorly understood. Studies on monozygotic genes, respectively (1). twins have helped discern the contributions of genetic ver- Although human fetal B lymphocytes rearrange and ex- sus environmental factors on expressed traits. In the present press a highly restricted set of VH genes (2–6), the frequency of experiments, we applied a novel anchored PCR-ELISA sys- Ig VH gene rearrangement in cord blood lymphocytes is tem to compare the heavy chain V gene (VH) subgroup rep- roughly proportional to VH family size (7). In adults, some ertoires of and ␥ expressing B lymphocytes from ten pairs genes such as VH 18/2, and VH 4.21 are expressed in high fre- of adult monozygotic twins, including eight pairs who are quency (8–10). Deletions or duplications of individual VH concordant or discordant for rheumatoid arthritis.