DOCSLIB.ORG

N Φ(N) Is the Order of This Group: Z• Φ(N) := | N|, the Number of Units in Zn

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
N Φ(N) Is the Order of This Group: Z• Φ(N) := | N|, the Number of Units in Zn MAS 6217 (Fall 2017) Number Theory and Cryptography (Yiu) Inquiry Based Learning Modules A – F (in lieu of September 7–14 class lectures) Name: 1. The Euler ϕ-function: number of units in Zn Let n> 1 be an integer. The units in Zn form a multiplicative subgroup Z• Z Z n := {[a] ∈ n : [a][b] = [1] for some b ∈ }. The Euler ϕ-function ϕ(n) is the order of this group: Z• ϕ(n) := | n|, the number of units in Zn. Exercise. For each integer n in the table below, list the units in Zn and the value of ϕ(n): n ϕ(n) units in Zn 2 3 4 5 6 8 9 10 20 27 1 2. The Euler ϕ-function is a multiplicative function Theorem 1. The Euler ϕ-function is a multiplicative function, i.e., if gcd(m,n)=1, then ϕ(mn)= ϕ(m)ϕ(n). Proof. Consider the natural mapping F : Zmn → Zm × Zn given by F ([x]mn)=([x]m, [x]n). (i) Why is F is well defined? (ii) Why is F is onto? Since the domain and the range have the cardinality, the function F is also one-to-one, and is a bijection. ′ Z• Z• Z• (iii) Why does F restrict to a function F : mn → m × n ? (iv) Show that F ′ is a bijection and that this completes the proof of the theorem. 3. Calculation of ϕ(n) (a) Let p be a prime. (i) What is ϕ(p) ? (ii) What is ϕ(pk) for an integer k ≥ 1 ? (b) Make use of the results in (a) to show that 1 ϕ(n)= n 1 − . p Yp|n Exercise. For each integer n in the table below, find the value of ϕ(n): n ϕ(n) Calculation 64 81 100 108 120 MAS 6217 (Fall 2017) Number Theory and Cryptography (Yiu) Inquiry Based Learning Module B (in lieu of September 7 class lecture) 4. Fermat-Euler theorem Theorem 2 (Fermat-Euler). If gcd(a,n)=1, aϕ(n) ≡ 1 (mod n). Proof. Consider the function fa : Zn → Zn given by fa([x])=[ax]. (a) Why is fa one-to-one? (b) Why is fa onto? Z• Z• (c) Why does fa induce a bijection n → n ? Z• This means that if x1,..., xϕ(n) are the elements of n, then [ax1],..., [axϕ(n)] is a permutation of the same ϕ(n) elements. In other words, [ax1] ··· [axϕ(n)]=[x1] ··· [xϕ(n)], or ϕ(n) (a − 1)x1 ··· xϕ(n) ≡ 0 (mod n). (d) Why can we conclude that aϕ(n) ≡ 1 (mod n) ? Corollary 3 (Fermat’s Little Theorem). Let p be a prime, and a an integer. If p does not divide a, then ap−1 ≡ 1 (mod p). Proof. Z• 5. The order of an element in n Z• ϕ(n) Let a ∈ n. By the Fermat-Euler theorem a = 1, there is a smallest d Z• positive integer d := ordern(a) such that a = 1 ∈ n. Such an integer is Z• called the order of a in n. Proposition 4. ordern(a) is a divisor of ϕ(n). Proof. Let t = ordern(a), and write ϕ(n)= tq + r for some integers q and r, 0 ≤ r<t. Assume r =06 . Obtain a contradiction by showing that ar ≡ 1 (mod n): Therefore, r = 0, and ϕ(n) = tq. From this ordern(a) is a divisor of ϕ(n). Z• Exercise. For each integer n below, consider the elements in n other than 1. Compute the order by listing its successive powers modulo n: (1) n = 12 with ϕ(n)=4: a ordern(a) powers of a mod 12 5 7 11 (2) n = 15 with ϕ(n)=8: a ordern(a) powers of a mod 15 2 4 7 8 11 13 14 (3) n = 13 with ϕ(n)=12. a ordern(a) powers of a mod 13 2 3 4 5 6 7 8 9 10 11 12 Proposition 5. If ordern(a)= t, then t order (ak)= . n gcd(t, k) Proof. Let d = gcd(t, k) and write t = dt′, k = dk′ for integers t′, k′. Note that gcd(t′, k′)=1. ′ (1) Show that (ak)t =1. ′′ (2) Suppose (ak)t = 1 for some t′′ < t′. Show that kt′′ is a multiple of t = dt′. This means that t′′ is a multiple of t′, an impossibility. k ′ t This shows that ordern(a )= t = d . 6. Primality test for Mersenne numbers p Theorem 6. Let p be a prime. Every prime divisor of Mp := 2 − 1 is of the form 2kp +1 for some integer k. Show that this follows from Fermat’s little theorem. 11 Exercise. (4). Show that M11 =2 − 1 = 2047 is composite by explicitly factoring it. 13 (5) Show that M13 =2 − 1 = 8191 is a prime. MAS 6217 (Fall 2017) Number Theory and Cryptography (Yiu) Inquiry Based Learning Module C (in lieu of September 12 class lecture) 7. The sum d|n ϕ(d) Lemma 7. IfPf(n) is a multiplicative function, then so is F (n) := d|n f(d). Proof. Let m and n be relatively prime. P F (mn)= f(d) dX|mn = F (m)F (n). Theorem 8. d|n ϕ(d)= n. Proof. Let F (Pn) := d|n ϕ(d). (1) For a prime powerP pk, show that F (pk)= pk. By Lemma 7, F is a multiplicative function. ki (2) Let n = pi . Show that F (n)= n. Q Therefore, d|n ϕ(d)= n. P 8. Gauss’ theorem Theorem 9 (Gauss). If F is a finite field, the multiplicative group F • = F \ {0} is a cyclic group. Proof. Let q = |F |. For each d|q − 1, suppose there ψ(d) elements of order d in F ∗ = F \ {0}. (a) Why is q − 1= d|q−1 ψ(d) ? P (b) Note that there are at most d elements in F satisfying xd − 1=0. Why? (c) In fact, if α is element of order d, then the elements satisfying xd−1= 0 are precisely 1, α, α2,..., αd−1. How many of these have order d? (d) Conclude that ψ(d)=0 or ϕ(d). (e) Make use of this and Theorem 8 to conclude that there are exactly ϕ(d) elements of order d. Corollary 10. Let p be an odd prime. Z• (a) For each divisor t of p − 1, there are exactly ϕ(t) elements of p = Zp \ {0} of order t. (b) There are exactly ϕ(p − 1) primitive roots for p. Proof. Z• 9. When is n cyclic? Lemma 11. A cyclic group has at most one element of order 2. Proof. Let G be a cyclic group of order n, and a ∈ G a generator, i.e., an element of order n. Every element of G is of the form ak for some k ≤ n. (a) What is the order of ak? (b) When is this order equal to 2? (c) Deduce that if n is odd, there is no element of order 2. (d) Show that if n is even, there is only one element of order 2. Z• Proposition 12. If m = ab for relatively prime integers a, b ≥ 3, then m cannot be cyclic. Proof. Let m = ab for relatively prime integers a, b ≥ 3. (a) Why are there integers x1 and x2 satisfying the following simultane- ous congruences? x1 ≡−1 (mod a) x2 ≡ 1 (mod a) and (x1 ≡ 1 (mod b) (x2 ≡−1 (mod b). Z• (b) How do x1 and x2 give distinct elements of ab of order 2? Z• This shows that m cannot be cyclic. Z• k k Theorem 13. m is cyclic if and only if m = 2, 4, or p , 2p for an odd prime p. Proof. (⇒) Suppose Zm is cyclic, and m is a prime power. (i) For m =2k, k ≥ 3, give two elements of order 2. Therefore, m =2, 4, or pk for an odd prime p and k ≥ 1. (ii) Suppose m = ab for a,b > 1 with gcd(a,b)=1. Why must one of a, b equal to 2? Therefore, m =2, 4, pk, or 2pk for an odd prime p and k ≥ 1. (⇐) Give a generator when (iii) m =2: (iv) m =4: Z• For an odd prime p, let b ∈ p be a generator. Z• p−1 In Module D, we shall show that it b ∈ p is a generator with b =1+ ap for an integer q, then Z (1) when a 6≡ 0 (mod p), b is a generator of pk , k > 1, Z (2) when a ≡ 0 (mod p), b + p is a generator of pk , k > 1. Z• k (v) Give a generator of m for m =2p by making use the above result. MAS 6217 (Fall 2017) Number Theory and Cryptography (Yiu) Inquiry Based Learning Module D (in lieu of September 12 class lecture) Z• Z Generators of pk in terms of those of p for an odd prime Let p be an odd prime. The following two propositions A and B establish Z the theorem on generators of pk for an odd prime p and k > 1. Z• Theorem 14. Let p be an odd prime, and b ∈ p a generator with bp−1 =1+ ap for an integer a. Let q = pk, k > 1. Z• (a) If a 6≡ 0 (mod p), then b is a generator of q. Z• (b) If a ≡ 0 (mod p), then b + p is a generator of q. Proposition A. Suppose a is not divisible by p.
Load more

Recommended publications
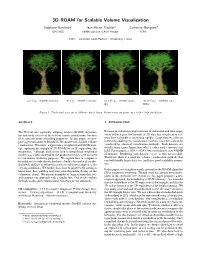
  • 3D ROAM for Scalable Volume Visualization
    3D ROAM for Scalable Volume Visualization St´ephane Marchesin∗ Jean-Michel Dischler† Catherine Mongenet‡ ICPS/IGG INRIA Lorraine, CALVI Project ICPS LSIIT { Universit´e Louis Pasteur { Strasbourg, France (a) 2.5 fps – 104000 tetrahedra (b) 1 fps – 380000 tetrahedra (c) 0.45 fps – 932000 tetrahe- (d) 0.15 fps – 3065000 tetra- dra hedra Figure 1: The bonsa¨ı data set at different detail levels. Frame rates are given for a 1024 × 1024 resolution ABSTRACT 1 INTRODUCTION The 2D real time optimally adapting meshes (ROAM) algorithm Because of continuous improvements in simulation and data acqui- has had wide success in the field of terrain visualization, because sition technologies, the amount of 3D data that visualization sys- of its efficient error-controlling properties. In this paper, we pro- tems have to handle is increasing rapidly. Large datasets offer an pose a generalization of ROAM in 3D suitable for scalable volume interesting challenge to visualization systems, since they cannot be visualization. Therefore, we perform a straightforward 2D/3D anal- visualized by classical visualization methods. Such datasets are ogy, replacing the triangle of 2D ROAM by its 3D equivalent, the usually many times larger than what a video card's memory can tetrahedron. Although work in the field of hierarchical tetrahedral hold. For example, a 1024×1024×446 voxel dataset uses 446MB meshes was widely undertaken, the produced meshes were not used of memory. Rendering such datasets ”as-is” is thus not possible. for volumetric rendering purposes. We explain how to compute a Therefore, there is a need for volume visualization methods that bounded error inside the tetrahedron to build a hierarchical tetrahe- can both handle larger data sets, and have good scalability proper- dral mesh and how to refine this mesh in real time to adapt it to the ties.
    [Show full text]
  • The Area of a Triangle
    Chapter 22 The area of a triangle 22.1 Heron’s formula for the area of a triangle Theorem 22.1. The area of a triangle of sidelengths a, b, c is given by = s(s a)(s b)(s c), △ − − − 1 p where s = 2 (a + b + c). B Ia I ra r A C Y Y ′ s − b s − c s − a Proof. Consider the incircle and the excircle on the opposite side of A. From the similarity of triangles AIZ and AI′Z′, r s a = − . ra s From the similarity of triangles CIY and I′CY ′, r r =(s b)(s c). · a − − 802 The area of a triangle From these, (s a)(s b)(s c) r = − − − , r s and the area of the triangle is = rs = s(s a)(s b)(s c). △ − − − p Exercise 1. Prove that 1 2 = (2a2b2 +2b2c2 +2c2a2 a4 b4 c4). △ 16 − − − 22.2 Heron triangles 803 22.2 Heron triangles A Heron triangle is an integer triangle whose area is also an integer. 22.2.1 The perimeter of a Heron triangle is even Proposition 22.2. The semiperimeter of a Heron triangle is an integer. Proof. It is enough to consider primitive Heron triangles, those whose sides are relatively prime. Note that modulo 16, each of a4, b4, c4 is congruent to 0 or 1, according as the number is even or odd. To render in (??) the sum 2a2b2 +2b2c2 +2c2a2 a4 b4 c4 0 modulo 16, exactly two of a, b, c must be odd. It− follows− that− the≡ perimeter of a Heron triangle must be an even number.
    [Show full text]
  • Volume 6 (2006) 1–16
    FORUM GEOMETRICORUM A Journal on Classical Euclidean Geometry and Related Areas published by Department of Mathematical Sciences Florida Atlantic University b bbb FORUM GEOM Volume 6 2006 http://forumgeom.fau.edu ISSN 1534-1178 Editorial Board Advisors: John H. Conway Princeton, New Jersey, USA Julio Gonzalez Cabillon Montevideo, Uruguay Richard Guy Calgary, Alberta, Canada Clark Kimberling Evansville, Indiana, USA Kee Yuen Lam Vancouver, British Columbia, Canada Tsit Yuen Lam Berkeley, California, USA Fred Richman Boca Raton, Florida, USA Editor-in-chief: Paul Yiu Boca Raton, Florida, USA Editors: Clayton Dodge Orono, Maine, USA Roland Eddy St. John’s, Newfoundland, Canada Jean-Pierre Ehrmann Paris, France Chris Fisher Regina, Saskatchewan, Canada Rudolf Fritsch Munich, Germany Bernard Gibert St Etiene, France Antreas P. Hatzipolakis Athens, Greece Michael Lambrou Crete, Greece Floor van Lamoen Goes, Netherlands Fred Pui Fai Leung Singapore, Singapore Daniel B. Shapiro Columbus, Ohio, USA Steve Sigur Atlanta, Georgia, USA Man Keung Siu Hong Kong, China Peter Woo La Mirada, California, USA Technical Editors: Yuandan Lin Boca Raton, Florida, USA Aaron Meyerowitz Boca Raton, Florida, USA Xiao-Dong Zhang Boca Raton, Florida, USA Consultants: Frederick Hoffman Boca Raton, Floirda, USA Stephen Locke Boca Raton, Florida, USA Heinrich Niederhausen Boca Raton, Florida, USA Table of Contents Khoa Lu Nguyen and Juan Carlos Salazar, On the mixtilinear incircles and excircles,1 Juan Rodr´ıguez, Paula Manuel and Paulo Semi˜ao, A conic associated with the Euler line,17 Charles Thas, A note on the Droz-Farny theorem,25 Paris Pamfilos, The cyclic complex of a cyclic quadrilateral,29 Bernard Gibert, Isocubics with concurrent normals,47 Mowaffaq Hajja and Margarita Spirova, A characterization of the centroid using June Lester’s shape function,53 Christopher J.
    [Show full text]
  • On Triangles As Real Analytic Varieties of an Extended Fermat Equation
    On Triangles as Real Analytic Varieties of an Extended Fermat Equation Giri Prabhakar∗ Abstract On the one hand, triangles play an important role in the solution of elliptic curves, as exemplified in studies by Tunnell on the congruent number problem, or Ono relating arbitrary triangles to elliptic curves. On the other hand, Frey-Hellegouarch curves are deeply connected to Fermat's equation. Thus, we are motivated to explore the relationship between triangles and Fermat's equation. We show that triangles in Euclidean space can be exactly described by real analytic varieties of an extension of the Fermat equation. To the 3 best of our knowledge, this formulation has not been explored previously. Let S = f(a; b; c) 2 R≥0 j (c > φ φ φ 0 ^ 9 φ 2 R≥1)[a + b = c ]g be the set of real non-negative solutions to the Fermat equation extended to admit real valued exponents φ ≥ 1, which we term the Fermat index. Let E be the set of triplets of side lengths of all non-degenerate and degenerate 2-simplices. We show that S = E, and that each triangle has a unique Fermat index. We show that there exists a deformation retraction F based on the extended Fermat equation, that maps all possible sides a ≤ c and b ≤ c of 2-simplices (a; b; c) 2 S, to the retract c of fixed length at a fixed angle to a. However, (a; b; c) is also governed by the law of cosines; thus an alternate map P exists based on the law of cosines, which must be geometrically identical to F .
    [Show full text]
  • Integer Trigonometry for Integer Angles
    Algorithms and Computation in Mathematics • Volume 26 Editors Arjeh M. Cohen Henri Cohen David Eisenbud Michael F. Singer Bernd Sturmfels For further volumes: http://www.springer.com/series/3339 Oleg Karpenkov Geometry of Continued Fractions Oleg Karpenkov Dept. of Mathematical Sciences University of Liverpool Liverpool, UK ISSN 1431-1550 Algorithms and Computation in Mathematics ISBN 978-3-642-39367-9 ISBN 978-3-642-39368-6 (eBook) DOI 10.1007/978-3-642-39368-6 Springer Heidelberg New York Dordrecht London Library of Congress Control Number: 2013946250 Mathematics Subject Classification (2010): 11J70, 11H06, 11P21, 52C05, 52C07 © Springer-Verlag Berlin Heidelberg 2013 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. Exempted from this legal reservation are brief excerpts in connection with reviews or scholarly analysis or material supplied specifically for the purpose of being entered and executed on a computer system, for exclusive use by the purchaser of the work. Duplication of this publication or parts thereof is permitted only under the provisions of the Copyright Law of the Publisher’s location, in its current version, and permission for use must always be obtained from Springer. Permissions for use may be obtained through RightsLink at the Copyright Clearance Center. Violations are liable to prosecution under the respective Copyright Law.
    [Show full text]
  • PROBLEMS in ELEMENTARY NUMBER THEORY Hojoo
    PROBLEMS IN ELEMENTARY NUMBER THEORY Hojoo Lee Version 050722 God does arithmetic. C. F. Gauss 1, −24, 252, −1472, 4830, −6048, −16744, 84480, −113643, −115920, 534612, −370944, −577738, 401856, 1217160, 987136, −6905934, 2727432, 10661420, −7109760, −4219488, −12830688, 18643272, 21288960, −25499225, 13865712, −73279080, 24647168, ··· 1 2 PROBLEMS IN ELEMENTARY NUMBER THEORY Contents 1. Introduction 3 2. Notations and Abbreviations 4 3. Divisibility Theory I 5 4. Divisibility Theory II 12 5. Arithmetic in Zn 16 Primitive Roots 16 Quadratic Residues 17 Congruences 17 6. Primes and Composite Numbers 20 Composite Numbers 20 Prime Numbers 20 7. Rational and Irrational Numbers 24 Rational Numbers 24 Irrational Numbers 25 8. Diophantine Equations I 29 9. Diophantine Equations II 34 10. Functions in Number Theory 37 Floor Function and Fractional Part Function 37 Euler phi Function 39 Divisor Functions 39 More Functions 40 Functional Equations 41 11. Polynomials 44 12. Sequences of Integers 46 Linear Recurrnces 46 Recursive Sequences 47 More Sequences 51 13. Combinatorial Number Theory 54 14. Additive Number Theory 61 15. The Geometry of Numbers 66 16. Miscellaneous Problems 67 17. Sources 71 18. References 94 PROBLEMS IN ELEMENTARY NUMBER THEORY 3 1. Introduction The heart of Mathematics is its problems. Paul Halmos 1. Introduction Number Theory is a beautiful branch of Mathematics. The purpose of this book is to present a collection of interesting questions in Number Theory. Many of the problems are mathematical competition problems all over the world including IMO, APMO, APMC, and Putnam, etc. The book is available at http://my.netian.com/∼ideahitme/orange.html 2.
    [Show full text]
  • Two Brahmagupta Problems
    Forum Geometricorum b Volume 6 (2006) 301–310. bbb FORUM GEOM ISSN 1534-1178 Two Brahmagupta Problems K. R. S. Sastry Abstract. D. E. Smith reproduces two problems from Brahmagupta’s work Ku- takh¯adyaka (algebra) in his History of Mathematics, Volume 1. One of them involves a broken tree and the other a mountain journey. Normally such objects are represented by vertical line segments. However, it is every day experience that such objects need not be vertical. In this paper, we generalize these situations to include slanted positions and provide integer solutions to these problems. 1. Introduction School textbooks on geometry and trigonometry contain problems about trees, poles, buildings, hills etc. to be solved using the Pythagorean theorem or trigono- metric ratios. The assumption is that such objects are vertical. However, trees grow not only vertically (and tall offering a magestic look) but also assume slanted positions (thereby offering an elegant look). Buildings too need not be vertical in structure, for example the leaning tower of Pisa. Also, a distant planar view of a mountain is more like a scalene triangle than a right one. In this paper we regard the angles formed in such situations as having rational cosines. We solve the fol- lowing Brahmagupta problems from [5] in the context of rational cosines triangles. In [4] these problems have been given Pythagorean solutions. Problem 1. A bamboo 18 cubits high was broken by the wind. Its tip touched the ground 6 cubits from the root. Tell the lengths of the segments of the bamboo. Problem 2. On the top of a certain hill live two ascetics.
    [Show full text]
  • Pythagorean Triangles
    Chapter 17 Pythagorean triangles 17.1 Primitive Pythagorean triples A Pythagorean triangle is one whose sidelengths are integers. An easy way to construct Pythagorean triangles is to take two distinct positive integers m>nand form (a, b, c)=(2mn, m2 − n2,m2 + n2). Then, a2 + b2 = c2. We call such a triple (a, b, c) a Pythagorean triple. The Pythagorean triangle has perimeter p =2m(m + n) and area A = mn(m2 − n2). B 2 n + 2 2mn m A m2 − n2 C A Pythagorean triple (a, b, c) is primitive if a, b, c do not have a common divisor (greater than 1). Every primitive Pythagorean triple is constructed by choosing m, n to be relatively prime and of opposite parity. 302 Pythagorean triangles 17.1.1 Rational angles The (acute) angles of a primitive Pythagorean triangle are called rational angles, since their trigonometric ratios are all rational. sin cos tan 2mn m2−n2 2mn A m2+n2 m2+n2 m2−n2 m2−n2 2mn m2−n2 B m2+n2 m2+n2 2mn A B More basic than these is the fact that tan 2 and tan 2 are rational: A n B m − n tan = , tan = . 2 m 2 m + n This is easily seen from the following diagram showning the incircle of the right triangle, which has r =(m − n)n. B n ) n + m ( (m + n)n ) n I r − m ( m r (m − n)n A m(m − n) (m − n)n C 17.1.2 Some basic properties of primitive Pythagorean triples 1. Exactly one leg is even.
    [Show full text]
  • California State University, Northridge an Annotated
    CALIFORNIA STATE UNIVERSITY, NORTHRIDGE AN ANNOTATED BIBLIOGRAPHY OF HEURISTICS FOR THE SECONDARY LEVEL (7-12) A graduate project submitted in partial satisfaction of the requirements for the degree of Master of Arts in Secondary Education by Jennifer Irene Conner June, 1980 Project Irene Conner is approved: H. Heimler, Advisor California State University, Northridge ii TABLE OF CONTENTS Chapter Page 1. INTRODUCTION 1 Purpose of Heuristics 1 History 2 Terminology 4 Strategies 7 Studies 10 Advantages and Disadvantages 13 References 18 2 . ANNOTATED BIBLIOGRAPHY 22 Algebra 23 Arithmetic 24 Calculator 31 Calculus 31 Geometry 32 Logic 39 Theory 39 iii ABSTRACT AN ANNOTATED BIBLIOGRAPHY OF HEURISTICS FOR THE SECONDARY LEVEL (7-12) by Jennifer Irene Conner Master of Arts in Secondary Education This graduate project is an annotated bibliography of articles written from 1975 through 1979 concerning the heuristic method of teaching and its applications in the classroom. The articles are from these professional Journals: Arithmetic Teacher, Mathematics Teacher, Mathematics Teaching, and School Science and Mathematics. To introduce the reader to the subject of heuristics, the following topics are presented: purpose, history, termi­ nology, strategies, studies, and advantages and disadvan­ tages. iv ' ' INTRODUCTION The use of heuristics, or simply heuristics, is a well- known method for the teaching and learning of mathematics. Often called "discovery learning," it challenges the student to think one's way through the problem at hand. Apart from a growing book-literature on the subject, numerous articles have appeared in professional journals. This graduate project is an annotated bibliography of such articles, for the period 1975-1979.
    [Show full text]
  • Tantalizing Triangles.Nb
    Tantalizing Triangles Ted Courant Berkeley Math Circle 29 March, 2016 [email protected] ◼ The Pythagorean Theorem In a right triangle, the sum of the squares of the sides equals the square of the hypotenuse. This is perhaps the most famous theorem in elementary mathematics. 1. Let a = m2 - n2, b = 2 m n, and c = m2 + n2. Prove that a2 + b2 = c2. Thus the pattern m2 - n2, 2 m n, m2 + n2 always yields a triple of integers whose sides form a right triangle; we call three such numbers a Pythagorean Triple 2. We will prove that all pythagorean triples arise according to this pattern! Recall the difference of squares identity: a2 - b2 = (a - b) (a + b). We can use this identity to verify that three numbers form a pythagorean triple. To verify that 202 + 212 = 292, compute 292 - 212 = 8·50 = 16·25 = 202 Done! 3. Show that the following are Pythagorean Triples: 99-101-200, 60-61-11, 8-15-17, 16-63-65. 4. Notice that 20-21-29 form the sides of a very nearly isosceles right triangle. Can you find other nearly isosceles right triangles, namely ones whose legs differ by 1? ◼ Viviani’s Theorem The perpendiculars to the sides, from any point inside an equilateral triangle, add up to the height of the triangle. In the second equilateral triangle above, the regions formed by the perpendiculars to the sides are formed; show that the red area equals the blue area. ◼ The Law of Cosines (and Sines) and applications Proof by altitudes: recall that the altitudes of a triangle meet at a point (the Orthocenter of the triangle).
    [Show full text]
  • Arxiv:Math/0510482V2
    COMPLETELY EMPTY PYRAMIDS ON INTEGER LATTICES AND TWO-DIMENSIONAL FACES OF MULTIDIMENSIONAL CONTINUED FRACTIONS. O. N. KARPENKOV Abstract. In this paper we develop an integer-affine classification of three-dimensional multistory completely empty convex marked pyramids. We apply it to obtain the com- plete lists of compact two-dimensional faces of multidimensional continued fractions lying in planes at integer distances to the origin equal 2, 3, 4, ... The faces are considered up to the action of the group of integer-linear transformations. In conclusion we formu- late some actual unsolved problems associated with the generalizations for n-dimensional faces and more complicated face configurations. Contents Introduction and background 2 0.1. General definitions 2 0.2. Definition of multidimensional continued fractions in the sense of Klein 3 0.3. Two-dimensional faces of multidimensional continued fractions 5 0.4. Description of the paper 6 1. Formulation of main results 6 1.1. Classification of two-dimensional multistory completely empty pyramids 6 1.2. Compact two-dimensional faces at distance greater than one 7 2. Proof of Theorem A 9 2.1. Preliminary definitions and statements 9 2.2. First results on empty integer tetrahedra 11 2.3. Proof of Theorem A for the case of polygonal marked pyramids 15 2.4. Proof of Theorem A for the case of triangular marked pyramids 19 arXiv:math/0510482v2 [math.NT] 12 Dec 2006 3. Proof of Theorem B 33 3.1. Completeness of Lists “αn” for n ≥ 2ofTheoremB 33 3.2. The completion of proof of Theorem B 34 4. Unsolved questions and problems 36 References 41 Date: 27 August 2006.
    [Show full text]
  • On Integer Geometry (22 March 2011)
    2. On integer geometry (22 March 2011) 2.1. Basic notions and definitions. A notion of geometry in general can be inter- preted in many different ways. In our course we think of geometry as of a set of objects and a congruence relation which is normally defined by some group of transformations. For instance, in Euclidean geometry in the plane we study points, lines, segments, poly- gons, circles, etc, the congruence relation is defined by the group of all length preserving transformations O(2; R) (or the orthogonal group). 2.1.1. Objects and congruence relation of integer geometry. While saying about planar lattice geometry we think of a lattice Z2 in R2. Any two lattices are isomorphic, so it does not matter which lattice to work with. While changing one lattice to another one should be careful only with Euclidean invariants that are not preserved by the isomorphisms, all the lattice invariants are preserved. For simplicity we mostly consider the integer lattice (containing points with both integer coordinates). The objects of integer (lattice) geometry are integer points, integer segments and polygons having all vertices in the integer lattice, integer lines passing through couples of lattice points, integer angles with vertices in lattice points. The congruence relation is defined by the group of affine transformations preserving the lattice, i.e. Aff(2; Z). This group is a semidirect product of GL(2; Z) and the group of translations on integer vectors. We use ”»=” to indicate that two objects are lattice congruent. The congruence relation is slightly different to the Euclidean case.
    [Show full text]