DOCSLIB.ORG

Some Construction Problems Related to the Incircle of a Triangle

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Some Construction Problems Related to the Incircle of a Triangle SOME CONSTRUCTION PROBLEMS RELATED TO THE INCIRCLE OF A TRIANGLE by Amy B. Bell A Thesis Submitted to the Faculty of The Charles E Schmidt College of Science In Partial Fulfillment of the Requirements for the Degree of Masters of Science in Teaching Florida Atlantic University Boca Raton, Florida December 2006 Some Construction Problem s R elated to the Incircle of a Triangle by Amy B. B ell This thesis was prepared under the direction of the candidate's thesis advisor, Dr. Paul Yiu, Department of Mathematical Sciences, and has been approved by the members of her supervisory committee. It was submitted to the faculty of the Charles E. Schmidt College of Science and was accepted in partial fulfi llment of the requirements for the degree of Master of Science in Teaching of Mathematics. SUPERVISORY COMMITTEE: I I i.. • I (C-v Thesis Advisor Date ll Acknowledgements I would like to thank my graduate advisor, Professor Paul Yiu, for his support, patience and encouragement throughout the process of this thesis. I would also like to thank Professor Markus Schmidmeier for going beyond the usual duties of a thesis committee member and giving valuable feedback that '\,. made my thesis defense much more effective. I would also like to acknowledge the support of my mother, Katherine Gosney and my husband, Terry Bell. Both made it possible for me to spend the additional hours I needed to work through the mathematical ideas presented in this thesis. 111 ~-- ----- --------------- - Abstract Author: Amy B. Bell Title: Some Construction Problems Related to the Incircle of a Triangle Institution: Florida Atlantic University Thesis Advisor: Dr. Paul Yiu Degree: Masters of Science in Teaching Year: 2006 This thesis explores several construction problems related to the incircle of a triangle. Firstly, as a generalization of a theorem of D. W. Hansen, we find two quadruples of quantities related to a triangle which have equal sums and equal sums of squares. We also study the construction problems of triangles with centroid on the incircle, and those with a specified cevian - a median, an angle bisector, or an altitude- bisected by the incircle. Detailed analysis leads to dE>•:;i[.>' s of animation pictures using the dynamic software Geometer's Sketchpad. lV Contents List of Tables . v11 List of Figures . vm 1 Preliminaries 1 1.1 Introduction .... .. ... .. ............ .. 1.2 Notations ... ...... ............ ...... .... .. .. 3 1.3 The Heron formula and Heron triangles . 4 1.3.1 The Heron formula. 4 1.3 .2 Heron triangles . ... ....... ..... .. ... .. .. 4 1.4 Barycentric coordinates . 5 1.4.1 Homogeneous barycentric coordinates . 5 1.4.2 Absolute barycentric coordinates . 6 1.4.3 Equation ofthe incircle . ......... .. .. ....... 7 1.5 Geometric constructions . 7 1.5.1 Geometric solution of quadratic equations . 7 1.5.2 Non-constructibility .... .. .. ... .. .. ... .. .... 8 2 Hansen's theorem and generalizations 9 2.1 Hansen's theorem . 9 2.2 Integer relations from Pythagorean triangles . 11 2.3 Generalization of Hansen's theorem . 13 2.4 Some triangle geometry . 15 2.5 ProofofTheorem 2.3 .. .... ... .. ...... .... .. 18 2.6 Converse ofHansen's Theorem .. ........... .. ... 19 v 2. 7 Integer relations . 21 3 Triangles with centroid on the incircle 24 3.1 From s- bands-c. 25 3.2 From band c ........ .. ...... ........ .. ....... 28 3.3 Triangle with a median trisected by the incircle . ... ... 32 ';; 4 Triangle with midpoint of one cevian on incircle '•3 ' 4.1 Construction of triangle ABC with midpoint of A-median on incircle . 34 4.1.1 From s - b and s - c . 34 4.1 .2 From band c ........................... .. 36 4.2 Construction of triangle ABC with midpoint of A-bisector on incircle ............................ 39 4.2.1 From b and c . 40 4.2.2 An alternative construction . 42 4.2.3 From s- b and s - c . 43 4.3 Construction of triangle ABC with midpoint of A-altitude on incircle ............................ 44 4.3.1 From band c . .................... .. ...... 45 4.3 .2 From s- bands-c. 46 Bibliography VI ---- -- - - ---- -- - --- - List of Tables Integers with equal sums and sums of squares from Pythagorean triangles ... .... ...................... ....... 12 2 Integers with equal sums and sums of squares from Heron triangles . 21 3 More integers with equal sums and sums of squares from Heron triangles .......................... ............. 23 Vll ------- ------- - -- - ----- - · - List of Figures 1.1 The incircle . 3 1.2 Homogeneous barycentric coordinates . 6 1.3 Solutions of quadratic equations . 8 2.1 The incircle of a right triangle . 9 2.2 The incircle and excircles of a right triangle . 10 2.3 Circumcenter and orthocenter . 13 'i'" 2.4 Two quadruples with equal sums and equal sums of squares . 14 2.5 Incenter and excenter . 15 2.6 ] 'f a= 2R . ........ ...... ... ...... .. ......... ....... 16 2.7 ra + r b + rc = 4R + r. 17 3.1 Isosceles with centroid on incircle .. ..... .. ... ... ....... 25 3.2 Construction of u from v and w . 26 3.3 Triangle with centroid on incircle . 27 3.4 Triangle with centroid on incircle . 28 2 1 2 4 2 3.5 AP = -(b+ c) + -(b- c) . ... ... .. .... ... .. .. ........ 29 5 5 3.6 Solution of (3 .3) . 30 3.7 Triangles with centroid on incircle . 31 3.8 Triangle with a median trisected by the incircle .... .......... 32 4.1 Isosceles triangle with median bisected by incircle . 34 4.2 Triangle with median bisected by incircle . 35 4.3 Triangle with median bisected by incircle . 36 4.4 Solution of(4.1) ... ...... .. ............ .. .. ..... 37 vm -------- --- 4.5 Triangle with a median bisected by incircle . 38 4.6 Triangle with a median bisected by incircle . 38 4.7 Barycentric coordinates of midpoint of angle bisector . 39 4.8 Construction of A . .... ... .. ... .... .......... 40 2 4.9 Triangle with an angle bisector bisected by incircle . 42 4.10 Triangle with an angle bisector bisected by incircle . 43 4.11 Triangle with two altitudes bisected by incircle . 45 ~ .. 1 1 1 4.12 -+-=- . .. .. .... .. .. .... .. .... .. .. .. .. 46 p q r 1 1 1 4.13 -+-=- .. ... ...... .. ..... ... ... ... .. ...... 47 V W X 4.14 Construction of u from v and w . .. .. .... .. .. ... .... 48 4.15 Triangle with an altitude bisected by incircle . 48 IX Chapter 1 Preliminaries 1.1 Introduction In thi s thesis we study several problems re lated to the inc irc le of a triang le. In the present chapter we sha ll ex pl a in some bac kground results in triangle geometry th at sha ll be freely used in the subsequent chapters, namely, ( i) the Heron formula for the area of a triang le and formulas for various radi i asso­ c iated with a triang le (s1 .3), (ii) the noti on of barycentric coordinates and the descriptio n of the inc irc le in terms of such ( ~ 1.4), (iii ) a basic meth od o f solvin g quadratic equati ons as a ruler and compass construc­ ti on problem (§ 1.5). In Chapter 2, we generali ze a result of D. W. Hansen [I] and prove (Theorem 2.3) that for a given triang le with orthocentcr H , the two quadruples, namely, (i) the inradius and th e three exradii, and (ii ) the c ircumdiameter and the lengths of the segments AH, D H , C H , have equal sums and equal sums of squares. In §2.6, we prove a strong converse of Hansen's theorem (Theorem 2.4). In chapter 3, we study the constructi on problem of a triangle whose inc ircle contains the centro id . We analyze the problem w ith two sets of g iven data: ( i) g iven two le ngth s band c, to construct a third le ngth a so that they form a triang le w hose incirc le contains the centroid ( >3 3.2): (ii ) g iven two po ints /3, C: together w ith a third po in t X on the segment I3C, to construct a third po in t A suc h that ABC has its inc irclc containing the centroid, and tangent to BC at X, (§3. 1). A ft e r a deta il ed analysis, we incorporate the constructions with the use of the Geometer's Sketchpad, a dy namic software for geometric construc tions. F inally, in C hapter 4 , we study a variation of the the me of C hapter 3, na me ly the constructi on probl em o f a triang le w hose inc irclc b isects one specifi c cevian of the tri ang le. Recall that a ccvian is a line through a vertex of the tri ang le. T he cevians we consider in C hapte r 4 are a median, a n ang le bisector, and an a ltitude. T hus, we analyze each proble m below to the exte nt that it is solvable as a rule r and compass constructi on pro ble m . In each suc h case, we produce a constructi on using the Geometer's Sketc hpad . (i) Given two le ngth s band r, to construct a third le ngth a so that they form a triang le w hose incirc lc b isects (a) th e median (§4. 1.2), (b) the ang le bisector (§4.2. I), (c) the altitude Cfi4.3. 1) on the side a . (ii) Given two points B, C togethe r with a thi rd po in t X on the segment BC, to construct a triang le ABC w ith inc irc le tangent to BC at X and bisecting (a) th e median (§4. 1. 1), (b) the angle bisector (§4.2.3 ), (c) the altitude (§4.3.2) on the s ide BC. 2 - - - ------------- --------- ---. 1.2 Notations We consider a triangle ABC with side length s B C = a, C A = !J , AJJ = c.
Load more

Recommended publications
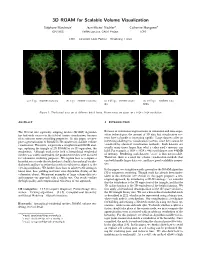
  • 3D ROAM for Scalable Volume Visualization
    3D ROAM for Scalable Volume Visualization St´ephane Marchesin∗ Jean-Michel Dischler† Catherine Mongenet‡ ICPS/IGG INRIA Lorraine, CALVI Project ICPS LSIIT { Universit´e Louis Pasteur { Strasbourg, France (a) 2.5 fps – 104000 tetrahedra (b) 1 fps – 380000 tetrahedra (c) 0.45 fps – 932000 tetrahe- (d) 0.15 fps – 3065000 tetra- dra hedra Figure 1: The bonsa¨ı data set at different detail levels. Frame rates are given for a 1024 × 1024 resolution ABSTRACT 1 INTRODUCTION The 2D real time optimally adapting meshes (ROAM) algorithm Because of continuous improvements in simulation and data acqui- has had wide success in the field of terrain visualization, because sition technologies, the amount of 3D data that visualization sys- of its efficient error-controlling properties. In this paper, we pro- tems have to handle is increasing rapidly. Large datasets offer an pose a generalization of ROAM in 3D suitable for scalable volume interesting challenge to visualization systems, since they cannot be visualization. Therefore, we perform a straightforward 2D/3D anal- visualized by classical visualization methods. Such datasets are ogy, replacing the triangle of 2D ROAM by its 3D equivalent, the usually many times larger than what a video card's memory can tetrahedron. Although work in the field of hierarchical tetrahedral hold. For example, a 1024×1024×446 voxel dataset uses 446MB meshes was widely undertaken, the produced meshes were not used of memory. Rendering such datasets ”as-is” is thus not possible. for volumetric rendering purposes. We explain how to compute a Therefore, there is a need for volume visualization methods that bounded error inside the tetrahedron to build a hierarchical tetrahe- can both handle larger data sets, and have good scalability proper- dral mesh and how to refine this mesh in real time to adapt it to the ties.
    [Show full text]
  • The Apollonius Problem on the Excircles and Related Circles
    Forum Geometricorum b Volume 6 (2006) xx–xx. bbb FORUM GEOM ISSN 1534-1178 The Apollonius Problem on the Excircles and Related Circles Nikolaos Dergiades, Juan Carlos Salazar, and Paul Yiu Abstract. We investigate two interesting special cases of the classical Apollo- nius problem, and then apply these to the tritangent of a triangle to find pair of perspective (or homothetic) triangles. Some new triangle centers are constructed. 1. Introduction This paper is a study of the classical Apollonius problem on the excircles and related circles of a triangle. Given a triad of circles, the Apollonius problem asks for the construction of the circles tangent to each circle in the triad. Allowing both internal and external tangency, there are in general eight solutions. After a review of the case of the triad of excircles, we replace one of the excircles by another (possibly degenerate) circle associated to the triangle. In each case we enumerate all possibilities, give simple constructions and calculate the radii of the circles. In this process, a number of new triangle centers with simple coordinates are constructed. We adopt standard notations for a triangle, and work with homogeneous barycen- tric coordinates. 2. The Apollonius problem on the excircles 2.1. Let Γ=((Ia), (Ib), (Ic)) be the triad of excircles of triangle ABC. The sidelines of the triangle provide 3 of the 8 solutions of the Apollonius problem, each of them being tangent to all three excircles. The points of tangency of the excircles with the sidelines are as follows. See Figure 2. BC CA AB (Ia) Aa =(0:s − b : s − c) Ba =(−(s − b):0:s) Ca =(−(s − c):s :0) (Ib) Ab =(0:−(s − a):s) Bb =(s − a :0:s − c) Cb =(s : −(s − c):0) (Ic) Ac =(0:s : −(s − a)) Bc =(s :0:−(s − c)) Cc =(s − a : s − b :0) Publication Date: Month day, 2006.
    [Show full text]
  • Stanley Rabinowitz, Arrangement of Central Points on the Faces of A
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 ©IJCDM Volume 5, 2020, pp. 13{41 Received 6 August 2020. Published on-line 30 September 2020 web: http://www.journal-1.eu/ ©The Author(s) This article is published with open access1. Arrangement of Central Points on the Faces of a Tetrahedron Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. We systematically investigate properties of various triangle centers (such as orthocenter or incenter) located on the four faces of a tetrahedron. For each of six types of tetrahedra, we examine over 100 centers located on the four faces of the tetrahedron. Using a computer, we determine when any of 16 con- ditions occur (such as the four centers being coplanar). A typical result is: The lines from each vertex of a circumscriptible tetrahedron to the Gergonne points of the opposite face are concurrent. Keywords. triangle centers, tetrahedra, computer-discovered mathematics, Eu- clidean geometry. Mathematics Subject Classification (2020). 51M04, 51-08. 1. Introduction Over the centuries, many notable points have been found that are associated with an arbitrary triangle. Familiar examples include: the centroid, the circumcenter, the incenter, and the orthocenter. Of particular interest are those points that Clark Kimberling classifies as \triangle centers". He notes over 100 such points in his seminal paper [10]. Given an arbitrary tetrahedron and a choice of triangle center (for example, the circumcenter), we may locate this triangle center in each face of the tetrahedron. We wind up with four points, one on each face.
    [Show full text]
  • Searching for the Center
    Searching For The Center Brief Overview: This is a three-lesson unit that discovers and applies points of concurrency of a triangle. The lessons are labs used to introduce the topics of incenter, circumcenter, centroid, circumscribed circles, and inscribed circles. The lesson is intended to provide practice and verification that the incenter must be constructed in order to find a point equidistant from the sides of any triangle, a circumcenter must be constructed in order to find a point equidistant from the vertices of a triangle, and a centroid must be constructed in order to distribute mass evenly. The labs provide a way to link this knowledge so that the students will be able to recall this information a month from now, 3 months from now, and so on. An application is included in each of the three labs in order to demonstrate why, in a real life situation, a person would want to create an incenter, a circumcenter and a centroid. NCTM Content Standard/National Science Education Standard: • Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships. • Use visualization, spatial reasoning, and geometric modeling to solve problems. Grade/Level: These lessons were created as a linking/remembering device, especially for a co-taught classroom, but can be adapted or used for a regular ed, or even honors level in 9th through 12th Grade. With more modification, these lessons might be appropriate for middle school use as well. Duration/Length: Lesson #1 45 minutes Lesson #2 30 minutes Lesson #3 30 minutes Student Outcomes: Students will: • Define and differentiate between perpendicular bisector, angle bisector, segment, triangle, circle, radius, point, inscribed circle, circumscribed circle, incenter, circumcenter, and centroid.
    [Show full text]
  • The Area of a Triangle
    Chapter 22 The area of a triangle 22.1 Heron’s formula for the area of a triangle Theorem 22.1. The area of a triangle of sidelengths a, b, c is given by = s(s a)(s b)(s c), △ − − − 1 p where s = 2 (a + b + c). B Ia I ra r A C Y Y ′ s − b s − c s − a Proof. Consider the incircle and the excircle on the opposite side of A. From the similarity of triangles AIZ and AI′Z′, r s a = − . ra s From the similarity of triangles CIY and I′CY ′, r r =(s b)(s c). · a − − 802 The area of a triangle From these, (s a)(s b)(s c) r = − − − , r s and the area of the triangle is = rs = s(s a)(s b)(s c). △ − − − p Exercise 1. Prove that 1 2 = (2a2b2 +2b2c2 +2c2a2 a4 b4 c4). △ 16 − − − 22.2 Heron triangles 803 22.2 Heron triangles A Heron triangle is an integer triangle whose area is also an integer. 22.2.1 The perimeter of a Heron triangle is even Proposition 22.2. The semiperimeter of a Heron triangle is an integer. Proof. It is enough to consider primitive Heron triangles, those whose sides are relatively prime. Note that modulo 16, each of a4, b4, c4 is congruent to 0 or 1, according as the number is even or odd. To render in (??) the sum 2a2b2 +2b2c2 +2c2a2 a4 b4 c4 0 modulo 16, exactly two of a, b, c must be odd. It− follows− that− the≡ perimeter of a Heron triangle must be an even number.
    [Show full text]
  • Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 ©IJCDM Volume 5, 2020, pp. 13{41 Received 6 August 2020. Published on-line 30 September 2020 web: http://www.journal-1.eu/ ©The Author(s) This article is published with open access1. Arrangement of Central Points on the Faces of a Tetrahedron Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. We systematically investigate properties of various triangle centers (such as orthocenter or incenter) located on the four faces of a tetrahedron. For each of six types of tetrahedra, we examine over 100 centers located on the four faces of the tetrahedron. Using a computer, we determine when any of 16 con- ditions occur (such as the four centers being coplanar). A typical result is: The lines from each vertex of a circumscriptible tetrahedron to the Gergonne points of the opposite face are concurrent. Keywords. triangle centers, tetrahedra, computer-discovered mathematics, Eu- clidean geometry. Mathematics Subject Classification (2020). 51M04, 51-08. 1. Introduction Over the centuries, many notable points have been found that are associated with an arbitrary triangle. Familiar examples include: the centroid, the circumcenter, the incenter, and the orthocenter. Of particular interest are those points that Clark Kimberling classifies as \triangle centers". He notes over 100 such points arXiv:2101.02592v1 [math.HO] 6 Jan 2021 in his seminal paper [10]. Given an arbitrary tetrahedron and a choice of triangle center (for example, the circumcenter), we may locate this triangle center in each face of the tetrahedron.
    [Show full text]
  • Triangle-Centers.Pdf
    Triangle Centers Maria Nogin (based on joint work with Larry Cusick) Undergraduate Mathematics Seminar California State University, Fresno September 1, 2017 Outline • Triangle Centers I Well-known centers F Center of mass F Incenter F Circumcenter F Orthocenter I Not so well-known centers (and Morley's theorem) I New centers • Better coordinate systems I Trilinear coordinates I Barycentric coordinates I So what qualifies as a triangle center? • Open problems (= possible projects) mass m mass m mass m Centroid (center of mass) C Mb Ma Centroid A Mc B Three medians in every triangle are concurrent. Centroid is the point of intersection of the three medians. mass m mass m mass m Centroid (center of mass) C Mb Ma Centroid A Mc B Three medians in every triangle are concurrent. Centroid is the point of intersection of the three medians. Centroid (center of mass) C mass m Mb Ma Centroid mass m mass m A Mc B Three medians in every triangle are concurrent. Centroid is the point of intersection of the three medians. Incenter C Incenter A B Three angle bisectors in every triangle are concurrent. Incenter is the point of intersection of the three angle bisectors. Circumcenter C Mb Ma Circumcenter A Mc B Three side perpendicular bisectors in every triangle are concurrent. Circumcenter is the point of intersection of the three side perpendicular bisectors. Orthocenter C Ha Hb Orthocenter A Hc B Three altitudes in every triangle are concurrent. Orthocenter is the point of intersection of the three altitudes. Euler Line C Ha Hb Orthocenter Mb Ma Centroid Circumcenter A Hc Mc B Euler line Theorem (Euler, 1765).
    [Show full text]
  • Volume 6 (2006) 1–16
    FORUM GEOMETRICORUM A Journal on Classical Euclidean Geometry and Related Areas published by Department of Mathematical Sciences Florida Atlantic University b bbb FORUM GEOM Volume 6 2006 http://forumgeom.fau.edu ISSN 1534-1178 Editorial Board Advisors: John H. Conway Princeton, New Jersey, USA Julio Gonzalez Cabillon Montevideo, Uruguay Richard Guy Calgary, Alberta, Canada Clark Kimberling Evansville, Indiana, USA Kee Yuen Lam Vancouver, British Columbia, Canada Tsit Yuen Lam Berkeley, California, USA Fred Richman Boca Raton, Florida, USA Editor-in-chief: Paul Yiu Boca Raton, Florida, USA Editors: Clayton Dodge Orono, Maine, USA Roland Eddy St. John’s, Newfoundland, Canada Jean-Pierre Ehrmann Paris, France Chris Fisher Regina, Saskatchewan, Canada Rudolf Fritsch Munich, Germany Bernard Gibert St Etiene, France Antreas P. Hatzipolakis Athens, Greece Michael Lambrou Crete, Greece Floor van Lamoen Goes, Netherlands Fred Pui Fai Leung Singapore, Singapore Daniel B. Shapiro Columbus, Ohio, USA Steve Sigur Atlanta, Georgia, USA Man Keung Siu Hong Kong, China Peter Woo La Mirada, California, USA Technical Editors: Yuandan Lin Boca Raton, Florida, USA Aaron Meyerowitz Boca Raton, Florida, USA Xiao-Dong Zhang Boca Raton, Florida, USA Consultants: Frederick Hoffman Boca Raton, Floirda, USA Stephen Locke Boca Raton, Florida, USA Heinrich Niederhausen Boca Raton, Florida, USA Table of Contents Khoa Lu Nguyen and Juan Carlos Salazar, On the mixtilinear incircles and excircles,1 Juan Rodr´ıguez, Paula Manuel and Paulo Semi˜ao, A conic associated with the Euler line,17 Charles Thas, A note on the Droz-Farny theorem,25 Paris Pamfilos, The cyclic complex of a cyclic quadrilateral,29 Bernard Gibert, Isocubics with concurrent normals,47 Mowaffaq Hajja and Margarita Spirova, A characterization of the centroid using June Lester’s shape function,53 Christopher J.
    [Show full text]
  • The Feuerbach Point and Euler Lines
    Forum Geometricorum b Volume 6 (2006) 191–197. bbb FORUM GEOM ISSN 1534-1178 The Feuerbach Point and Euler lines Bogdan Suceav˘a and Paul Yiu Abstract. Given a triangle, we construct three triangles associated its incircle whose Euler lines intersect on the Feuerbach point, the point of tangency of the incircle and the nine-point circle. By studying a generalization, we show that the Feuerbach point in the Euler reflection point of the intouch triangle, namely, the intersection of the reflections of the line joining the circumcenter and incenter in the sidelines of the intouch triangle. 1. A MONTHLY problem Consider a triangle ABC with incenter I, the incircle touching the sides BC, CA, AB at D, E, F respectively. Let Y (respectively Z) be the intersection of DF (respectively DE) and the line through A parallel to BC.IfE and F are the midpoints of DZ and DY , then the six points A, E, F , I, E, F are on the same circle. This is Problem 10710 of the American Mathematical Monthly with slightly different notations. See [3]. Y A Z Ha F E E F I B D C Figure 1. The triangle Ta and its orthocenter Here is an alternative solution. The circle in question is indeed the nine-point circle of triangle DY Z. In Figure 1, ∠AZE = ∠CDE = ∠CED = ∠AEZ. Therefore AZ = AE. Similarly, AY = AF . It follows that AY = AF = AE = AZ, and A is the midpoint of YZ. The circle through A, E, F , the midpoints of the sides of triangle DY Z, is the nine-point circle of the triangle.
    [Show full text]
  • On Triangles As Real Analytic Varieties of an Extended Fermat Equation
    On Triangles as Real Analytic Varieties of an Extended Fermat Equation Giri Prabhakar∗ Abstract On the one hand, triangles play an important role in the solution of elliptic curves, as exemplified in studies by Tunnell on the congruent number problem, or Ono relating arbitrary triangles to elliptic curves. On the other hand, Frey-Hellegouarch curves are deeply connected to Fermat's equation. Thus, we are motivated to explore the relationship between triangles and Fermat's equation. We show that triangles in Euclidean space can be exactly described by real analytic varieties of an extension of the Fermat equation. To the 3 best of our knowledge, this formulation has not been explored previously. Let S = f(a; b; c) 2 R≥0 j (c > φ φ φ 0 ^ 9 φ 2 R≥1)[a + b = c ]g be the set of real non-negative solutions to the Fermat equation extended to admit real valued exponents φ ≥ 1, which we term the Fermat index. Let E be the set of triplets of side lengths of all non-degenerate and degenerate 2-simplices. We show that S = E, and that each triangle has a unique Fermat index. We show that there exists a deformation retraction F based on the extended Fermat equation, that maps all possible sides a ≤ c and b ≤ c of 2-simplices (a; b; c) 2 S, to the retract c of fixed length at a fixed angle to a. However, (a; b; c) is also governed by the law of cosines; thus an alternate map P exists based on the law of cosines, which must be geometrically identical to F .
    [Show full text]
  • Degree of Triangle Centers and a Generalization of the Euler Line
    Beitr¨agezur Algebra und Geometrie Contributions to Algebra and Geometry Volume 51 (2010), No. 1, 63-89. Degree of Triangle Centers and a Generalization of the Euler Line Yoshio Agaoka Department of Mathematics, Graduate School of Science Hiroshima University, Higashi-Hiroshima 739–8521, Japan e-mail: [email protected] Abstract. We introduce a concept “degree of triangle centers”, and give a formula expressing the degree of triangle centers on generalized Euler lines. This generalizes the well known 2 : 1 point configuration on the Euler line. We also introduce a natural family of triangle centers based on the Ceva conjugate and the isotomic conjugate. This family contains many famous triangle centers, and we conjecture that the de- gree of triangle centers in this family always takes the form (−2)k for some k ∈ Z. MSC 2000: 51M05 (primary), 51A20 (secondary) Keywords: triangle center, degree of triangle center, Euler line, Nagel line, Ceva conjugate, isotomic conjugate Introduction In this paper we present a new method to study triangle centers in a systematic way. Concerning triangle centers, there already exist tremendous amount of stud- ies and data, among others Kimberling’s excellent book and homepage [32], [36], and also various related problems from elementary geometry are discussed in the surveys and books [4], [7], [9], [12], [23], [26], [41], [50], [51], [52]. In this paper we introduce a concept “degree of triangle centers”, and by using it, we clarify the mutual relation of centers on generalized Euler lines (Proposition 1, Theorem 2). Here the term “generalized Euler line” means a line connecting the centroid G and a given triangle center P , and on this line an infinite number of centers lie in a fixed order, which are successively constructed from the initial center P 0138-4821/93 $ 2.50 c 2010 Heldermann Verlag 64 Y.
    [Show full text]
  • The Feuerbach Point and the Fuhrmann Triangle
    Forum Geometricorum Volume 16 (2016) 299–311. FORUM GEOM ISSN 1534-1178 The Feuerbach Point and the Fuhrmann Triangle Nguyen Thanh Dung Abstract. We establish a few results on circles through the Feuerbach point of a triangle, and their relations to the Fuhrmann triangle. The Fuhrmann triangle is perspective with the circumcevian triangle of the incenter. We prove that the perspectrix is the tangent to the nine-point circle at the Feuerbach point. 1. Feuerbach point and nine-point circles Given a triangle ABC, we consider its intouch triangle X0Y0Z0, medial trian- gle X1Y1Z1, and orthic triangle X2Y2Z2. The famous Feuerbach theorem states that the incircle (X0Y0Z0) and the nine-point circle (N), which is the common cir- cumcircle of X1Y1Z1 and X2Y2Z2, are tangent internally. The point of tangency is the Feuerbach point Fe. In this paper we adopt the following standard notation for triangle centers: G the centroid, O the circumcenter, H the orthocenter, I the incenter, Na the Nagel point. The nine-point center N is the midpoint of OH. A Y2 Fe Y0 Z1 Y1 Z0 H O Z2 I T Oa B X0 U X2 X1 C Ja Figure 1 Proposition 1. Let ABC be a non-isosceles triangle. (a) The triangles FeX0X1, FeY0Y1, FeZ0Z1 are directly similar to triangles AIO, BIO, CIO respectively. (b) Let Oa, Ob, Oc be the reflections of O in IA, IB, IC respectively. The lines IOa, IOb, IOc are perpendicular to FeX1, FeY1, FeZ1 respectively. Publication Date: July 25, 2016. Communicating Editor: Paul Yiu. 300 T. D. Nguyen Proof.
    [Show full text]