Supplementary Information For
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Plasma Membrane Ca2+–Atpase in Rat and Human Odontoblasts Mediates Dentin Mineralization
biomolecules Article Plasma Membrane Ca2+–ATPase in Rat and Human Odontoblasts Mediates Dentin Mineralization Maki Kimura 1,†, Hiroyuki Mochizuki 1,†, Ryouichi Satou 2, Miyu Iwasaki 2, Eitoyo Kokubu 3, Kyosuke Kono 1, Sachie Nomura 1, Takeshi Sakurai 1, Hidetaka Kuroda 1,4,† and Yoshiyuki Shibukawa 1,*,† 1 Department of Physiology, Tokyo Dental College, 2-9-18, Kanda-Misaki-cho, Chiyoda-ku, Tokyo 101-0061, Japan; [email protected] (M.K.); [email protected] (H.M.); [email protected] (K.K.); [email protected] (S.N.); [email protected] (T.S.); [email protected] (H.K.) 2 Department of Epidemiology and Public Health, Tokyo Dental College, Chiyodaku, Tokyo 101-0061, Japan; [email protected] (R.S.); [email protected] (M.I.) 3 Department of Microbiology, Tokyo Dental College, Chiyodaku, Tokyo 101-0061, Japan; [email protected] 4 Department of Dental Anesthesiology, Kanagawa Dental University, 1-23, Ogawacho, Kanagawa, Yokosuka-shi 238-8570, Japan * Correspondence: [email protected] † These authors contributed equally to this study. Abstract: Intracellular Ca2+ signaling engendered by Ca2+ influx and mobilization in odontoblasts is critical for dentinogenesis induced by multiple stimuli at the dentin surface. Increased Ca2+ is exported by the Na+–Ca2+ exchanger (NCX) and plasma membrane Ca2+–ATPase (PMCA) to Citation: Kimura, M.; Mochizuki, H.; maintain Ca2+ homeostasis. We previously demonstrated a functional coupling between Ca2+ Satou, R.; Iwasaki, M.; Kokubu, E.; extrusion by NCX and its influx through transient receptor potential channels in odontoblasts. Kono, K.; Nomura, S.; Sakurai, T.; Although the presence of PMCA in odontoblasts has been previously described, steady-state levels of Kuroda, H.; Shibukawa, Y. -

Identification and Partial Characterization of a Family of Putative Palmitoyltransferases in Dictyostelium Discoideum Brent Elliot Wells
The University of Maine DigitalCommons@UMaine Electronic Theses and Dissertations Fogler Library 2003 Identification and Partial Characterization of a Family of Putative Palmitoyltransferases in Dictyostelium Discoideum Brent Elliot Wells Follow this and additional works at: http://digitalcommons.library.umaine.edu/etd Part of the Biochemistry Commons Recommended Citation Wells, Brent Elliot, "Identification and Partial Characterization of a Family of Putative Palmitoyltransferases in Dictyostelium Discoideum" (2003). Electronic Theses and Dissertations. 301. http://digitalcommons.library.umaine.edu/etd/301 This Open-Access Thesis is brought to you for free and open access by DigitalCommons@UMaine. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of DigitalCommons@UMaine. IDENTIFICATION AND PARTIAL CHARACTERIZATION OF A FAMILY OF PUTATIVE PALMITOYLTRANSFERASES IN DICTYOSTELIUM DISCOIDEUM BY Brent Elliott Wells B.S. University of Utah, 1994 A THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science (in Biochemistry) The Graduate School The University of Maine December, 2003 Advisory Committee: Robert E. Gundersen, Associate Professor of Biochemistry, Advisor Keith W. Hutchison, Professor of Biochemistry Mary Rumpho-Kennedy, Professor of Biochemistry LIBRARY RIGHTS STATEMENT In presenting this thesis in partial fulfillment of the requirements for an advanced degree at The University of Maine, I agree that the Library shall make it freely available for inspection. I further agree that permission for "fair use" copying of this thesis for scholarly purposes may be granted by the Librarian. It is understood that any copying or publication of this thesis for financial gain shall not be allowed without my written permission. -

Inorganic Pyrophosphatase Is a Component of the Drosophila Nucleosome Remodeling Factor Complex
Downloaded from genesdev.cshlp.org on October 3, 2021 - Published by Cold Spring Harbor Laboratory Press Inorganic pyrophosphatase is a component of the Drosophila nucleosome remodeling factor complex David A. Gdula, Raphael Sandaltzopoulos, Toshio Tsukiyama,1 Vincent Ossipow, and Carl Wu2 Laboratory of Molecular Cell Biology, National Cancer Institute, National Institutes of Health, Bethesda, Maryland 20892-4255 USA The Drosophila nucleosome remodeling factor (NURF) is a protein complex consisting of four polypeptides that facilitates the perturbation of chromatin structure in vitro in an ATP-dependent manner. The 140-kD NURF subunit, imitation switch (ISWI), is related to the SWI2/SNF2 ATPase. Another subunit, NURF-55, is a 55-kD WD repeat protein homologous to the human retinoblastoma-associated protein RbAp48. Here, we report the cloning and characterization of the smallest (38 kD) component of NURF. NURF-38 is strikingly homologous to known inorganic pyrophosphatases. Both recombinant NURF-38 alone and the purified NURF complex are shown to have inorganic pyrophosphatase activity. Inhibition of the pyrophosphatase activity of NURF with sodium fluoride has no significant effect on chromatin remodeling, indicating that these two activities may be biochemically uncoupled. Our results suggest that NURF-38 may serve a structural or regulatory role in the complex. Alternatively, because accumulation of unhydrolyzed pyrophosphate during nucleotide incorporation inhibits polymerization, NURF may also have been adapted to deliver pyrophosphatase -

SERCA in Genesis of Arrhythmias: What We Already Know and What Is New?
Review 43 SERCA in genesis of arrhythmias: what we already know and what is new? Nilüfer Erkasap Department of Physiology, Medical Faculty, Eskiflehir Osmangazi University, Eskiflehir, Turkey ABSTRACT This review mainly focuses on the structure, function of the sarco(endo)plasmic reticulum calcium pump (SERCA) and its role in genesis of arrhythmias. SERCA is a membrane protein that belongs to the family of P-type ion translocating ATPases and pumps free cytosolic calcium into intracellular stores. Active transport of Ca2+ is achieved, according to the E1-E2 model, changing of SERCA structure by Ca2+. The affinity of Ca2+ -binding sites varies from high (E1) to low (E2). Three different SERCA genes were identified-SERCA1, SERCA2, and SERCA3. SERCA is mainly represented by the SERCA2a isoform in the heart. In heart muscle, during systole, depolarization triggers the release of Ca2+ from the sarcoplasmic reticulum (SR) and starts contraction. During diastole, muscle relaxation occurs as Ca2+ is again removed from cytosol, predominantly by accumulation into SR via the action of SERCA2a. The main regulator of SERCA2a is phospholamban and another regulator proteolipid of SERCA is sarcolipin. There are a lot of studies on the effect of decreased and/or increased SERCA activity in genesis of arrhythmia. Actually both decrease and increase of SERCA activity in the heart result in some pathological mechanisms such as heart failure and arrhythmia. (Anadolu Kardiyol Derg 2007: 7 Suppl 1; 43-6) Key words: sarco(endo)plasmic reticulum, SERCA, arrhythmia, calcium channels Introduction from cytosol, predominantly by accumulation into sarcoplasmic reticulum via the action of sarco(endo)plasmic reticulum Cardiac physiology is a major area of research in basic and Ca ATPase (SERCA). -
Type of the Paper (Article
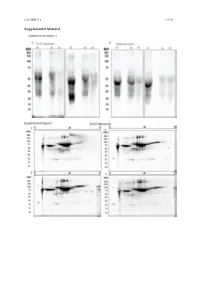
Cells 2020, 9, x 1 of 19 Supplemental Material Cells 2020, 9, x 2 of 19 Figure S1. Secretome enrichment: protocol optimization. 1D SDS-PAGE documentation of washing steps: Culture medium was substituted with FCS-free medium, which was changed every 2 h. The supernatants were then collected, and the proteins isolated and separated in 1D SDS-PAGE ((A) TK173 and (B) TK188). Proteins were stained with Flamingo fluorescent gel stain. Two-dimensional pattern of the proteins isolated from supernatant of TK173, (C) 2 h, (D) 4 h, (E) 6 h, and (F) 8 h after changing to FCS-free medium. (G) Cell secretome collected 24 h after elimination of the contaminating FCS-proteins with different washing steps. Proteins were stained with Flamingo fluorescent gel stain. Cells 2020, 9, x 3 of 19 Figure S2. 2-DE reference maps of secretomes; 150 μg proteins were loaded on an 11 cm IPG strip with a linear pH gradient PI 5–8 for IEF; 12% SDS-polyacrylamide gels were used for the second dimension. Proteins were stained with Flamingo fluorescent gel stain. Identified spots were assigned a number corresponding to that in their table. 2-DE maps from secretome of (A) TK173 control and (B) TGFβ1- treated ones. The 2-DE patterns revealed an alteration of secretome in stimulated TK173. Secretome patterns from TK173 treated with (C) ANG II and (D) PDGF. Cells 2020, 9, x 4 of 19 A Figure S3. Classification of the differentially expressed proteins upon ANG II, TGFβ1, or PDGF treatment in TK173. (A) Bar charts of the cellular component analyzed by STRAP biological function analysis in which the identified proteins from all treatments in both cell types are involved. -

The Structural Basis for Pyrophosphatase Catalysis
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Research Article 1491 The structural basis for pyrophosphatase catalysis Pirkko Heikinheimo1,2, Jukka Lehtonen1,2, Alexander Baykov3, Reijo Lahti2, Barry S Cooperman4* and Adrian Goldman1,2* Background: Soluble inorganic pyrophosphatase (PPase), an essential Addresses: 1Turku Centre for Biotechnology, PO enzyme central to phosphorus metabolism, catalyzes the hydrolysis of the phos- Box 123, FIN-20521 Turku, Finland, 2Department phoanhydride bond in inorganic pyrophosphate. Catalysis requires divalent of Biochemistry, University of Turku, FIN-20014 Turku, Finland, 3A.N. Belozersky Institute of metal ions which affect the apparent pKas of the essential general acid and Physico-Chemical Biology, Moscow State base on the enzyme, and the pKa of the substrate. Three to five metal ions are University, Moscow 119899, Russia and required for maximal activity, depending on pH and enzyme source. A detailed 4Department of Chemistry, University of understanding of catalysis would aid both in understanding the nature of biolog- Pennsylvania, Philadelphia, PA 19104, USA. ical mechanisms of phosphoryl transfer, and in understanding the role of diva- *Corresponding authors. lent cations. Without a high-resolution complex structure such a model has E-mail: [email protected] previously been unobtainable. E-mail: [email protected] Key words: mechanism, phosphoanhydride Results: We report the first two high-resolution structures of yeast PPase, at hydrolysis, phosphoryl transfer, pyrophosphatase, 2.2 and 2.0 Å resolution with R factors of around 17 %. One structure contains refinement, structure the two activating metal ions; the other, the product (MnPi)2 as well. -

Endoplasmic Reticulum Potassium–Hydrogen Exchanger and Small
Research Article 625 Endoplasmic reticulum potassium–hydrogen exchanger and small conductance calcium-activated potassium channel activities are essential for ER calcium uptake in neurons and cardiomyocytes Malle Kuum1,2,3, Vladimir Veksler2,3, Joanna Liiv1, Renee Ventura-Clapier2,3 and Allen Kaasik1,* 1Department of Pharmacology, Centre of Excellence for Translational Medicine, University of Tartu, Ravila 19, Tartu EE-51014, Estonia 2INSERM, U-769, 5, rue Jean-Baptiste Clement, Chaˆtenay-Malabry F-92296, France 3Universite´ Paris-Sud, 5, rue Jean-Baptiste Clement, Chaˆtenay-Malabry F-92296, France *Author for correspondence ([email protected]) Accepted 12 September 2011 Journal of Cell Science 125, 625–633 ß 2012. Published by The Company of Biologists Ltd doi: 10.1242/jcs.090126 Summary Calcium pumping into the endoplasmic reticulum (ER) lumen is thought to be coupled to a countertransport of protons through sarcoplasmic/endoplasmic reticulum calcium ATPase (SERCA) and the members of the ClC family of chloride channels. However, pH in the ER lumen remains neutral, which suggests a mechanism responsible for proton re-entry. We studied whether cation–proton exchangers could act as routes for such a re-entry. ER Ca2+ uptake was measured in permeabilized immortalized hypothalamic neurons, primary rat cortical neurons and mouse cardiac fibers. Replacement of K+ in the uptake solution with Na+ or tetraethylammonium led to a strong inhibition of Ca2+ uptake in neurons and cardiomyocytes. Furthermore, inhibitors of the potassium–proton exchanger (quinine or propranolol) but not of the sodium–proton exchanger reduced ER Ca2+ uptake by 56–82%. Externally added nigericin, a potassium– + proton exchanger, attenuated the inhibitory effect of propranolol. -

In Vivo Mapping of a GPCR Interactome Using Knockin Mice
In vivo mapping of a GPCR interactome using knockin mice Jade Degrandmaisona,b,c,d,e,1, Khaled Abdallahb,c,d,1, Véronique Blaisb,c,d, Samuel Géniera,c,d, Marie-Pier Lalumièrea,c,d, Francis Bergeronb,c,d,e, Catherine M. Cahillf,g,h, Jim Boulterf,g,h, Christine L. Lavoieb,c,d,i, Jean-Luc Parenta,c,d,i,2, and Louis Gendronb,c,d,i,j,k,2 aDépartement de Médecine, Université de Sherbrooke, Sherbrooke, QC J1H 5N4, Canada; bDépartement de Pharmacologie–Physiologie, Université de Sherbrooke, Sherbrooke, QC J1H 5N4, Canada; cFaculté de Médecine et des Sciences de la Santé, Université de Sherbrooke, Sherbrooke, QC J1H 5N4, Canada; dCentre de Recherche du Centre Hospitalier Universitaire de Sherbrooke, Sherbrooke, QC J1H 5N4, Canada; eQuebec Network of Junior Pain Investigators, Sherbrooke, QC J1H 5N4, Canada; fDepartment of Psychiatry and Biobehavioral Sciences, University of California, Los Angeles, CA 90095; gSemel Institute for Neuroscience and Human Behavior, University of California, Los Angeles, CA 90095; hShirley and Stefan Hatos Center for Neuropharmacology, University of California, Los Angeles, CA 90095; iInstitut de Pharmacologie de Sherbrooke, Sherbrooke, QC J1H 5N4, Canada; jDépartement d’Anesthésiologie, Université de Sherbrooke, Sherbrooke, QC J1H 5N4, Canada; and kQuebec Pain Research Network, Sherbrooke, QC J1H 5N4, Canada Edited by Brian K. Kobilka, Stanford University School of Medicine, Stanford, CA, and approved April 9, 2020 (received for review October 16, 2019) With over 30% of current medications targeting this family of attenuates pain hypersensitivities in several chronic pain models proteins, G-protein–coupled receptors (GPCRs) remain invaluable including neuropathic, inflammatory, diabetic, and cancer pain therapeutic targets. -

Crystal Structure of the Calcium Pump of Sarcoplasmic Reticulum at 2.6 AÊ Resolution
articles Crystal structure of the calcium pump of sarcoplasmic reticulum at 2.6 AÊ resolution Chikashi Toyoshima*², Masayoshi Nakasako*²³, Hiromi Nomura* & Haruo Ogawa* * Institute of Molecular and Cellular Biosciences, The University of Tokyo, Bunkyo-ku, Tokyo 113-0032, Japan ² The Harima Institute, The Institute of Physical and Chemical Research, Sayo-gun, Hyo-go 679-5143, Japan ³ PRESTO, Japan Science and Technology Corporation, Kawaguchi 332-0012, Japan ............................................................................................................................................................................................................................................................................ Calcium ATPase is a member of the P-type ATPases that transport ions across the membrane against a concentration gradient. Here we have solved the crystal structure of the calcium ATPase of skeletal muscle sarcoplasmic reticulum (SERCA1a) at 2.6 AÊ resolution with two calcium ions bound in the transmembrane domain, which comprises ten a-helices. The two calcium ions are located side by side and are surrounded by four transmembrane helices, two of which are unwound for ef®cient coordination geometry. The cytoplasmic region consists of three well separated domains, with the phosphorylation site in the central catalytic domain and the adenosine-binding site on another domain. The phosphorylation domain has the same fold as haloacid dehalogenase. Comparison with a low-resolution electron density map of the enzyme in the absence -

Clinical Significance of P‑Class Pumps in Cancer (Review)
ONCOLOGY LETTERS 22: 658, 2021 Clinical significance of P‑class pumps in cancer (Review) SOPHIA C. THEMISTOCLEOUS1*, ANDREAS YIALLOURIS1*, CONSTANTINOS TSIOUTIS1, APOSTOLOS ZARAVINOS2,3, ELIZABETH O. JOHNSON1 and IOANNIS PATRIKIOS1 1Department of Medicine, School of Medicine; 2Department of Life Sciences, School of Sciences, European University Cyprus, 2404 Nicosia, Cyprus; 3College of Medicine, Member of Qatar University Health, Qatar University, 2713 Doha, Qatar Received January 25, 2021; Accepted Apri 12, 2021 DOI: 10.3892/ol.2021.12919 Abstract. P‑class pumps are specific ion transporters involved Contents in maintaining intracellular/extracellular ion homeostasis, gene transcription, and cell proliferation and migration in all 1. Introduction eukaryotic cells. The present review aimed to evaluate the 2. Methodology role of P‑type pumps [Na+/K+ ATPase (NKA), H+/K+ ATPase 3. NKA (HKA) and Ca2+‑ATPase] in cancer cells across three fronts, 4. SERCA pump namely structure, function and genetic expression. It has 5. HKA been shown that administration of specific P‑class pumps 6. Clinical studies of P‑class pump modulators inhibitors can have different effects by: i) Altering pump func‑ 7. Concluding remarks and future perspectives tion; ii) inhibiting cell proliferation; iii) inducing apoptosis; iv) modifying metabolic pathways; and v) induce sensitivity to chemotherapy and lead to antitumor effects. For example, 1. Introduction the NKA β2 subunit can be downregulated by gemcitabine, resulting in increased apoptosis of cancer cells. The sarco‑ The movement of ions across a biological membrane is a endoplasmic reticulum calcium ATPase can be inhibited by crucial physiological process necessary for maintaining thapsigargin resulting in decreased prostate tumor volume, cellular homeostasis. -

ALLOSTERIC REGULATION of GS on AGONIST, ANTAGONIST and INVERSE AGONIST BINDING to the Β2ar by Gisselle A. Vélez Ruiz a Dissert
ALLOSTERIC REGULATION OF GS ON AGONIST, ANTAGONIST AND INVERSE AGONIST BINDING TO THE β2AR by Gisselle A. Vélez Ruiz A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Cellular and Molecular Biology) in the University of Michigan 2011 Doctoral Committee: Associate Professor Roger K. Sunahara, Chair Professor Richard R. Neubig Professor Michael D. Uhler Associate Professor Martin Myers Associate Professor John J.G. Tesmer To my family especially my mom and siblings, best friends: Grisel and Nelly, and to my boyfriend Osvaldo. Your constant love, support and eternal encouragement gave me the strength and motivation to accomplish my goals. ii ACKNOWLEDGEMENTS I would like to thank my mentor Roger Sunahara for all his support and endless enthusiasm. His support and patience allowed me to become a great researcher. I would also like to thank all the members of the Sunahara lab, past and present, especially Dr. Matthew Whorton and Dr. Adam Kuszak. Thank you for all your help and motivation especially when science was not on my side. Thank you for the great science but most importantly for the laughs; not matter how bad my day was they always found a way to make me laugh and I was always happy to be in lab even if I was not working. I would also like to thank Brian DeVree for all his help and endless conversations about GPCR theory and the implications of our research; a lot of those were documented here. I was extremely fortunate to have great collaborators that not only provided me with all the reagents I needed but also were key in making my project a success. -

Physiological and Pathophysiological Functions of the Ecto-Nucleotide Pyrophosphatase/Phosphodiesterase Family
CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector Biochimica et Biophysica Acta 1638 (2003) 1–19 www.bba-direct.com Review Physiological and pathophysiological functions of the ecto-nucleotide pyrophosphatase/phosphodiesterase family James W. Godinga, Bert Grobbenb, Herman Slegersb,* a Department of Pathology and Immunology, Monash Medical School, Monash University, Prahran 3181, Victoria, Australia b Department of Biomedical Sciences, Cellular Biochemistry, University of Antwerp, Universitaire Instelling Antwerpen, Universiteitplein 1, B-2610 Antwerpen-Wilrijk, Belgium Received 6 February 2003; received in revised form 20 March 2003; accepted 3 April 2003 Abstract The ecto-nucleotide pyrophosphatase/phosphodiesterase (E-NPP) multigene family contains five members. NPP1-3 are type II transmembrane metalloenzymes characterized by a similar modular structure composed of a short intracellular domain, a single transmembrane domain and an extracellular domain containing a conserved catalytic site. The short intracellular domain of NPP1 has a basolateral membrane-targeting signal while NPP3 is targeted to the apical surface of polarized cells. NPP4-5 detected by database searches have a predicted type I membrane orientation but have not yet been functionally characterized. E-NPPs have been detected in almost all tissues often confined to specific substructures or cell types. In some cell types, NPP1 expression is constitutive or can be induced by TGF-h and glucocorticoids, but the signal transduction pathways that control expression are poorly documented. NPP1-3 have a broad substrate specificity which may reflect their role in a host of physiological and biochemical processes including bone mineralization, calcification of ligaments and joint capsules, modulation of purinergic receptor signalling, nucleotide recycling, and cell motility.