DOCSLIB.ORG

Data Analysis: Simple Statistical Tests

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Data Analysis: Simple Statistical Tests VOLUME 3, ISSUE 6 Data Analysis: Simple Statistical Tests It’s the middle of summer, prime should use. Remember, continuous time for swimming, and your local variables are numeric (such as age in CONTRIBUTORS hospital reports several children with years or weight) while categorical vari- Escherichia coli O157:H7 infection. ables (whether yes or no, male or fe- Authors: A preliminary investigation shows male, or something else entirely) are Meredith Anderson, MPH that many of these children recently just what the name says—categories. swam in a local lake. The lake has For continuous variables, we generally Amy Nelson, PhD, MPH been closed so the health depart- calculate measures such as the mean FOCUS Workgroup* ment can conduct an investigation. (average), median and standard de- Now you need to find out whether Reviewers: viation to describe what the variable swimming in the lake is significantly looks like. We use means and medi- FOCUS Workgroup* associated with E. coli infection, so ans in public health all the time; for Production Editors: you’ll know whether the lake is the example, we talk about the mean age real culprit in the outbreak. This Tara P. Rybka, MPH of people infected with E. coli, or the situation occurred in Washington in Lorraine Alexander, DrPH median number of household con- 1999, and it’s one example of the tacts for case-patients with chicken Rachel Wilfert, MPH importance of good data analysis, pox. Editor in chief: including statistical testing, in an outbreak investigation. (1) In a field investigation, you are often Pia D.M. MacDonald, PhD, MPH interested in dichotomous or binary The major steps in basic data analy- (2-level) categorical variables that sis are: cleaning data, coding and represent an exposure (ate potato conducting descriptive analyses; salad or did not eat potato salad) or * All members of the FOCUS calculating estimates (with confi- an outcome (had Salmonella infection dence intervals); calculating meas- Workgroup are named on the last or did not have Salmonella infection). ures of association (with confidence page of this issue. For categorical variables, we cannot intervals); and statistical testing. calculate the mean or median, but we In earlier issues of FOCUS we dis- can calculate risk. Remember, risk is cussed data cleaning, coding and the number of people who develop a descriptive analysis, as well as calcu- disease among all the people at risk lation of estimates (risk and odds) of developing the disease during a and measures of association (risk given time period. For example, in a ratios and odds ratios). In this issue, group of firefighters, we might talk we will discuss confidence intervals about the risk of developing respira- and p-values, and introduce some tory disease during the month follow- basic statistical tests, including chi ing an episode of severe smoke inha- square and ANOVA. lation. Before starting any data analysis, it is important to know what types of The North Carolina Center for Public Health Prepared- Measures of Association variables you are working with. The ness is funded by Grant/Cooperative Agreement Num- ber U90/CCU424255 from the Centers for Disease types of variables tell you which esti- We usually collect information on ex- Control and Prevention. The contents of this publication mates you can calculate, and later, posure and disease because we want are solely the responsibility of the authors and do not which types of statistical tests you to compare two or more groups of necessarily represent the views of the CDC. North Carolina Center for Public Health Preparedness—The North Carolina Institute for Public Health FOCUS ON FIELD EPIDEMIOLOGY Page 2 people. To do this, we calculate measures of association. Table 1. Sample 2x2 table for Hepatitis A at Restaurant A. Measures of association tell us the strength of the asso- ciation between two variables, such as an exposure and a Outcome disease. The two measures of association that we use No Hepatitis Hepatitis A Total most often are the relative risk, or risk ratio (RR), and the A odds ratio (OR). The decision to calculate an RR or an OR depends on the study design (see box below). We inter- Ate salsa 218 45 263 Exposure pret the RR and OR as follows: Did not 21 85 106 RR or OR = 1: exposure has no association with disease eat salsa RR or OR > 1: exposure may be positively associated Total 239 130 369 with disease authors did. They found an odds ratio of 19.6*, meaning RR or OR < 1: exposure may be negatively associated that the odds of getting Hepatitis A among people who ate with disease salsa were 19.6 times as high as among people who did This is a good time to discuss one of our favorite analysis not eat salsa. tools—the 2x2 table. You should be familiar with 2x2 ta- *OR = ad = (218)(85) = 19.6 bles from previous FOCUS issues. They are commonly bc (45)(21) used with dichotomous variables to compare groups of people. The table has one dichotomous variable along the Confidence Intervals rows and another dichotomous variable along the col- umns. This set-up is useful because we usually are inter- How do we know whether an odds ratio of 19.6 is mean- ested in determining the association between a dichoto- ingful in our investigation? We can start by calculating the mous exposure and a dichotomous outcome. For exam- confidence interval (CI) around the odds ratio. When we ple, the exposure might be eating salsa at a restaurant (or calculate an estimate (like risk or odds), or a measure of not eating salsa), and the outcome might be Hepatitis A (or association (like a risk ratio or an odds ratio), that number no Hepatitis A). Table 1 displays data from a case-control (in this case 19.6) is called a point estimate. The confi- study conducted in Pennsylvania in 2003. (2) dence interval of a point estimate describes the precision of the estimate. It represents a range of values on either So what measure of association can we get from this 2x2 side of the estimate. The narrower the confidence inter- table? Since we do not know the total population at risk val, the more precise the point estimate. (3) Your point (everyone who ate salsa), we cannot determine the risk of estimate will usually be the middle value of your confi- illness among the exposed and unexposed groups. That dence interval. means we should not use the risk ratio. Instead, we will calculate the odds ratio, which is exactly what the study An analogy can help explain the confidence interval. Say we have a large bag of 500 red, green, and blue marbles. Risk ratio or odds ratio? We are interested in knowing the percentage of green mar- bles, but we do not have the time to count every marble. The risk ratio, or relative risk, is used when we look at a So we shake up the bag and select 50 marbles to give us population and compare the outcomes of those who an idea, or an estimate, of the percentage of green mar- were exposed to something to the outcomes of those bles in the bag. In our sample of 50 marbles, we find 15 who were not exposed. When we conduct a cohort green marbles, 10 red marbles, and 25 blue marbles. study, we can calculate risk ratios. Based on this sample, we can conclude that 30% (15 out However, the case-control study design does not allow us of 50) of the marbles in the bag are green. In this exam- to calculate risk ratios, because the entire population at ple, 30% is the point estimate. Do we feel confident in risk is not included in the study. That’s why we use odds stating that 30% of the marbles are green? We might ratios for case-control studies. An odds ratio is the odds have some uncertainty about this statement, since there is of exposure among cases divided by the odds of expo- a chance that the actual percent of green marbles in the sure among controls, and it provides a rough estimate of entire bag is higher or lower than 30%. In other words, our the risk ratio. sample of 50 marbles may not accurately reflect the ac- So remember, for a cohort study, calculate a risk ratio, tual distribution of marbles in the whole bag of 500 mar- and for a case-control study, calculate an odds ratio. For bles. One way to determine the degree of our uncertainty more information about calculating risk ratios and odds is to calculate a confidence interval. ratios, take a look at FOCUS Volume 3, Issues 1 and 2. North Carolina Center for Public Health Preparedness—The North Carolina Institute for Public Health VOLUME 3, ISSUE 6 Page 3 Calculating Confidence Intervals Ideally, we would like a very narrow confidence interval, So how do you calculate a confidence interval? It’s cer- which would indicate that our estimate is very precise. tainly possible to do so by hand. Most of the time, how- One way to get a more precise estimate is to take a larger ever, we use statistical programs such as Epi Info, SAS, sample. If we had taken 100 marbles (instead of 50) from STATA, SPSS, or Episheet to do the calculations. The our bag and found 30 green marbles, the point estimate default is usually a 95% confidence interval, but this can would still be 30%, but the 95% confidence interval would be adjusted to 90%, 99%, or any other level depending be a range of 21-39% (instead of our original range of 17- on the desired level of precision.
Load more

Recommended publications
  • Descriptive Statistics (Part 2): Interpreting Study Results
    Statistical Notes II Descriptive statistics (Part 2): Interpreting study results A Cook and A Sheikh he previous paper in this series looked at ‘baseline’. Investigations of treatment effects can be descriptive statistics, showing how to use and made in similar fashion by comparisons of disease T interpret fundamental measures such as the probability in treated and untreated patients. mean and standard deviation. Here we continue with descriptive statistics, looking at measures more The relative risk (RR), also sometimes known as specific to medical research. We start by defining the risk ratio, compares the risk of exposed and risk and odds, the two basic measures of disease unexposed subjects, while the odds ratio (OR) probability. Then we show how the effect of a disease compares odds. A relative risk or odds ratio greater risk factor, or a treatment, can be measured using the than one indicates an exposure to be harmful, while relative risk or the odds ratio. Finally we discuss the a value less than one indicates a protective effect. ‘number needed to treat’, a measure derived from the RR = 1.2 means exposed people are 20% more likely relative risk, which has gained popularity because of to be diseased, RR = 1.4 means 40% more likely. its clinical usefulness. Examples from the literature OR = 1.2 means that the odds of disease is 20% higher are used to illustrate important concepts. in exposed people. RISK AND ODDS Among workers at factory two (‘exposed’ workers) The probability of an individual becoming diseased the risk is 13 / 116 = 0.11, compared to an ‘unexposed’ is the risk.
    [Show full text]
  • Levels of Evidence Table
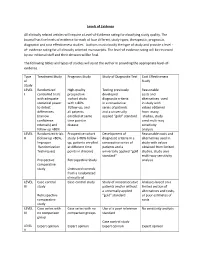
    Levels of Evidence All clinically related articles will require a Level-of-Evidence rating for classifying study quality. The Journal has five levels of evidence for each of four different study types; therapeutic, prognostic, diagnostic and cost effectiveness studies. Authors must classify the type of study and provide a level - of- evidence rating for all clinically oriented manuscripts. The level-of evidence rating will be reviewed by our editorial staff and their decision will be final. The following tables and types of studies will assist the author in providing the appropriate level-of- evidence. Type Treatment Study Prognosis Study Study of Diagnostic Test Cost Effectiveness of Study Study LEVEL Randomized High-quality Testing previously Reasonable I controlled trials prospective developed costs and with adequate cohort study diagnostic criteria alternatives used statistical power with > 80% in a consecutive in study with to detect follow-up, and series of patients values obtained differences all patients and a universally from many (narrow enrolled at same applied “gold” standard studies, study confidence time point in used multi-way intervals) and disease sensitivity follow up >80% analysis LEVEL Randomized trials Prospective cohort Development of Reasonable costs and II (follow up <80%, study (<80% follow- diagnostic criteria in a alternatives used in Improper up, patients enrolled consecutive series of study with values Randomization at different time patients and a obtained from limited Techniques) points in disease) universally
    [Show full text]
  • Meta-Analysis of Proportions
    NCSS Statistical Software NCSS.com Chapter 456 Meta-Analysis of Proportions Introduction This module performs a meta-analysis of a set of two-group, binary-event studies. These studies have a treatment group (arm) and a control group. The results of each study may be summarized as counts in a 2-by-2 table. The program provides a complete set of numeric reports and plots to allow the investigation and presentation of the studies. The plots include the forest plot, radial plot, and L’Abbe plot. Both fixed-, and random-, effects models are available for analysis. Meta-Analysis refers to methods for the systematic review of a set of individual studies with the aim to combine their results. Meta-analysis has become popular for a number of reasons: 1. The adoption of evidence-based medicine which requires that all reliable information is considered. 2. The desire to avoid narrative reviews which are often misleading. 3. The desire to interpret the large number of studies that may have been conducted about a specific treatment. 4. The desire to increase the statistical power of the results be combining many small-size studies. The goals of meta-analysis may be summarized as follows. A meta-analysis seeks to systematically review all pertinent evidence, provide quantitative summaries, integrate results across studies, and provide an overall interpretation of these studies. We have found many books and articles on meta-analysis. In this chapter, we briefly summarize the information in Sutton et al (2000) and Thompson (1998). Refer to those sources for more details about how to conduct a meta- analysis.
    [Show full text]
  • Limitations of the Odds Ratio in Gauging the Performance of a Diagnostic, Prognostic, Or Screening Marker
    American Journal of Epidemiology Vol. 159, No. 9 Copyright © 2004 by the Johns Hopkins Bloomberg School of Public Health Printed in U.S.A. All rights reserved DOI: 10.1093/aje/kwh101 Limitations of the Odds Ratio in Gauging the Performance of a Diagnostic, Prognostic, or Screening Marker Margaret Sullivan Pepe1,2, Holly Janes2, Gary Longton1, Wendy Leisenring1,2,3, and Polly Newcomb1 1 Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, WA. 2 Department of Biostatistics, University of Washington, Seattle, WA. 3 Division of Clinical Research, Fred Hutchinson Cancer Research Center, Seattle, WA. Downloaded from Received for publication June 24, 2003; accepted for publication October 28, 2003. A marker strongly associated with outcome (or disease) is often assumed to be effective for classifying persons http://aje.oxfordjournals.org/ according to their current or future outcome. However, for this assumption to be true, the associated odds ratio must be of a magnitude rarely seen in epidemiologic studies. In this paper, an illustration of the relation between odds ratios and receiver operating characteristic curves shows, for example, that a marker with an odds ratio of as high as 3 is in fact a very poor classification tool. If a marker identifies 10% of controls as positive (false positives) and has an odds ratio of 3, then it will correctly identify only 25% of cases as positive (true positives). The authors illustrate that a single measure of association such as an odds ratio does not meaningfully describe a marker’s ability to classify subjects. Appropriate statistical methods for assessing and reporting the classification power of a marker are described.
    [Show full text]
  • Guidance for Industry E2E Pharmacovigilance Planning
    Guidance for Industry E2E Pharmacovigilance Planning U.S. Department of Health and Human Services Food and Drug Administration Center for Drug Evaluation and Research (CDER) Center for Biologics Evaluation and Research (CBER) April 2005 ICH Guidance for Industry E2E Pharmacovigilance Planning Additional copies are available from: Office of Training and Communication Division of Drug Information, HFD-240 Center for Drug Evaluation and Research Food and Drug Administration 5600 Fishers Lane Rockville, MD 20857 (Tel) 301-827-4573 http://www.fda.gov/cder/guidance/index.htm Office of Communication, Training and Manufacturers Assistance, HFM-40 Center for Biologics Evaluation and Research Food and Drug Administration 1401 Rockville Pike, Rockville, MD 20852-1448 http://www.fda.gov/cber/guidelines.htm. (Tel) Voice Information System at 800-835-4709 or 301-827-1800 U.S. Department of Health and Human Services Food and Drug Administration Center for Drug Evaluation and Research (CDER) Center for Biologics Evaluation and Research (CBER) April 2005 ICH Contains Nonbinding Recommendations TABLE OF CONTENTS I. INTRODUCTION (1, 1.1) ................................................................................................... 1 A. Background (1.2) ..................................................................................................................2 B. Scope of the Guidance (1.3)...................................................................................................2 II. SAFETY SPECIFICATION (2) .....................................................................................
    [Show full text]
  • Contingency Tables Are Eaten by Large Birds of Prey
    Case Study Case Study Example 9.3 beginning on page 213 of the text describes an experiment in which fish are placed in a large tank for a period of time and some Contingency Tables are eaten by large birds of prey. The fish are categorized by their level of parasitic infection, either uninfected, lightly infected, or highly infected. It is to the parasites' advantage to be in a fish that is eaten, as this provides Bret Hanlon and Bret Larget an opportunity to infect the bird in the parasites' next stage of life. The observed proportions of fish eaten are quite different among the categories. Department of Statistics University of Wisconsin|Madison Uninfected Lightly Infected Highly Infected Total October 4{6, 2011 Eaten 1 10 37 48 Not eaten 49 35 9 93 Total 50 45 46 141 The proportions of eaten fish are, respectively, 1=50 = 0:02, 10=45 = 0:222, and 37=46 = 0:804. Contingency Tables 1 / 56 Contingency Tables Case Study Infected Fish and Predation 2 / 56 Stacked Bar Graph Graphing Tabled Counts Eaten Not eaten 50 40 A stacked bar graph shows: I the sample sizes in each sample; and I the number of observations of each type within each sample. 30 This plot makes it easy to compare sample sizes among samples and 20 counts within samples, but the comparison of estimates of conditional Frequency probabilities among samples is less clear. 10 0 Uninfected Lightly Infected Highly Infected Contingency Tables Case Study Graphics 3 / 56 Contingency Tables Case Study Graphics 4 / 56 Mosaic Plot Mosaic Plot Eaten Not eaten 1.0 0.8 A mosaic plot replaces absolute frequencies (counts) with relative frequencies within each sample.
    [Show full text]
  • Patient Safety Culture and Associated Factors Among Health Care Providers in Bale Zone Hospitals, Southeast Ethiopia: an Institutional Based Cross-Sectional Study
    Drug, Healthcare and Patient Safety Dovepress open access to scientific and medical research Open Access Full Text Article ORIGINAL RESEARCH Patient Safety Culture and Associated Factors Among Health Care Providers in Bale Zone Hospitals, Southeast Ethiopia: An Institutional Based Cross-Sectional Study This article was published in the following Dove Press journal: Drug, Healthcare and Patient Safety Musa Kumbi1 Introduction: Patient safety is a serious global public health issue and a critical component of Abduljewad Hussen 1 health care quality. Unsafe patient care is associated with significant morbidity and mortality Abate Lette1 throughout the world. In Ethiopia health system delivery, there is little practical evidence of Shemsu Nuriye2 patient safety culture and associated factors. Therefore, this study aims to assess patient safety Geroma Morka3 culture and associated factors among health care providers in Bale Zone hospitals. Methods: A facility-based cross-sectional study was undertaken using the “Hospital Survey 1 Department of Public Health, Goba on Patient Safety Culture (HSOPSC)” questionnaire. A total of 518 health care providers Referral Hospital, Madda Walabu University, Goba, Ethiopia; 2Department were interviewed. Analysis of variance (ANOVA) was employed to examine statistical of Public Health, College of Health differences between hospitals and patient safety culture dimensions. We also computed Science and Medicine, Wolayta Sodo internal consistency coefficients and exploratory factor analysis. Bivariate and multivariate University, Sodo, Ethiopia; 3Department of Nursing, Goba Referral Hospital, linear regression analyses were performed using SPSS version 20. The level of significance Madda Walabu University, Goba, Ethiopia was established using 95% confidence intervals and a p-value of <0.05. Results: The overall level of patient safety culture was 44% (95% CI: 43.3–44.6) with a response rate of 93.2%.
    [Show full text]
  • Relative Risks, Odds Ratios and Cluster Randomised Trials . (1)
    1 Relative Risks, Odds Ratios and Cluster Randomised Trials Michael J Campbell, Suzanne Mason, Jon Nicholl Abstract It is well known in cluster randomised trials with a binary outcome and a logistic link that the population average model and cluster specific model estimate different population parameters for the odds ratio. However, it is less well appreciated that for a log link, the population parameters are the same and a log link leads to a relative risk. This suggests that for a prospective cluster randomised trial the relative risk is easier to interpret. Commonly the odds ratio and the relative risk have similar values and are interpreted similarly. However, when the incidence of events is high they can differ quite markedly, and it is unclear which is the better parameter . We explore these issues in a cluster randomised trial, the Paramedic Practitioner Older People’s Support Trial3 . Key words: Cluster randomized trials, odds ratio, relative risk, population average models, random effects models 1 Introduction Given two groups, with probabilities of binary outcomes of π0 and π1 , the Odds Ratio (OR) of outcome in group 1 relative to group 0 is related to Relative Risk (RR) by: . If there are covariates in the model , one has to estimate π0 at some covariate combination. One can see from this relationship that if the relative risk is small, or the probability of outcome π0 is small then the odds ratio and the relative risk will be close. One can also show, using the delta method, that approximately (1). ________________________________________________________________________________ Michael J Campbell, Medical Statistics Group, ScHARR, Regent Court, 30 Regent St, Sheffield S1 4DA [email protected] 2 Note that this result is derived for non-clustered data.
    [Show full text]
  • Quasi-Experimental Studies in the Fields of Infection Control and Antibiotic Resistance, Ten Years Later: a Systematic Review
    HHS Public Access Author manuscript Author ManuscriptAuthor Manuscript Author Infect Control Manuscript Author Hosp Epidemiol Manuscript Author . Author manuscript; available in PMC 2019 November 12. Published in final edited form as: Infect Control Hosp Epidemiol. 2018 February ; 39(2): 170–176. doi:10.1017/ice.2017.296. Quasi-experimental Studies in the Fields of Infection Control and Antibiotic Resistance, Ten Years Later: A Systematic Review Rotana Alsaggaf, MS, Lyndsay M. O’Hara, PhD, MPH, Kristen A. Stafford, PhD, MPH, Surbhi Leekha, MBBS, MPH, Anthony D. Harris, MD, MPH, CDC Prevention Epicenters Program Department of Epidemiology and Public Health, University of Maryland School of Medicine, Baltimore, Maryland. Abstract OBJECTIVE.—A systematic review of quasi-experimental studies in the field of infectious diseases was published in 2005. The aim of this study was to assess improvements in the design and reporting of quasi-experiments 10 years after the initial review. We also aimed to report the statistical methods used to analyze quasi-experimental data. DESIGN.—Systematic review of articles published from January 1, 2013, to December 31, 2014, in 4 major infectious disease journals. METHODS.—Quasi-experimental studies focused on infection control and antibiotic resistance were identified and classified based on 4 criteria: (1) type of quasi-experimental design used, (2) justification of the use of the design, (3) use of correct nomenclature to describe the design, and (4) statistical methods used. RESULTS.—Of 2,600 articles, 173 (7%) featured a quasi-experimental design, compared to 73 of 2,320 articles (3%) in the previous review (P<.01). Moreover, 21 articles (12%) utilized a study design with a control group; 6 (3.5%) justified the use of a quasi-experimental design; and 68 (39%) identified their design using the correct nomenclature.
    [Show full text]
  • Statistical Analysis 8: Two-Way Analysis of Variance (ANOVA)
    Statistical Analysis 8: Two-way analysis of variance (ANOVA) Research question type: Explaining a continuous variable with 2 categorical variables What kind of variables? Continuous (scale/interval/ratio) and 2 independent categorical variables (factors) Common Applications: Comparing means of a single variable at different levels of two conditions (factors) in scientific experiments. Example: The effective life (in hours) of batteries is compared by material type (1, 2 or 3) and operating temperature: Low (-10˚C), Medium (20˚C) or High (45˚C). Twelve batteries are randomly selected from each material type and are then randomly allocated to each temperature level. The resulting life of all 36 batteries is shown below: Table 1: Life (in hours) of batteries by material type and temperature Temperature (˚C) Low (-10˚C) Medium (20˚C) High (45˚C) 1 130, 155, 74, 180 34, 40, 80, 75 20, 70, 82, 58 2 150, 188, 159, 126 136, 122, 106, 115 25, 70, 58, 45 type Material 3 138, 110, 168, 160 174, 120, 150, 139 96, 104, 82, 60 Source: Montgomery (2001) Research question: Is there difference in mean life of the batteries for differing material type and operating temperature levels? In analysis of variance we compare the variability between the groups (how far apart are the means?) to the variability within the groups (how much natural variation is there in our measurements?). This is why it is called analysis of variance, abbreviated to ANOVA. This example has two factors (material type and temperature), each with 3 levels. Hypotheses: The 'null hypothesis' might be: H0: There is no difference in mean battery life for different combinations of material type and temperature level And an 'alternative hypothesis' might be: H1: There is a difference in mean battery life for different combinations of material type and temperature level If the alternative hypothesis is accepted, further analysis is performed to explore where the individual differences are.
    [Show full text]
  • Antiretroviral Adverse Drug Reactions Pharmacovigilance in Harare City
    bioRxiv preprint doi: https://doi.org/10.1101/358069; this version posted June 28, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. 1 Original Manuscript 2 Title: Antiretroviral Adverse Drug Reactions Pharmacovigilance in Harare City, 3 Zimbabwe, 2017 4 Hamufare Mugauri1, Owen Mugurungi2, Tsitsi Juru1, Notion Gombe1, Gerald 5 Shambira1 ,Mufuta Tshimanga1 6 7 1. Department of Community Medicine, University of Zimbabwe 8 2. Ministry of Health and Child Care, Zimbabwe 9 10 Corresponding author: 11 Tsitsi Juru [email protected] 12 Office 3-66 Kaguvi Building, Cnr 4th/Central Avenue 13 University of Zimbabwe, Harare, Zimbabwe 14 Phone: +263 4 792157, Mobile: +263 772 647 465 1 bioRxiv preprint doi: https://doi.org/10.1101/358069; this version posted June 28, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. 15 Abstract 16 Introduction: Key to pharmacovigilance is spontaneously reporting all Adverse Drug 17 Reactions (ADR) during post-market surveillance. This facilitates identification and 18 evaluation of previously unreported ADR’s, acknowledging the trade-off between 19 benefits and potential harm of medications. Only 41% ADR’s documented in Harare 20 city clinical records for January to December 2016 were reported to Medicines 21 Control Authority of Zimbabwe (MCAZ).
    [Show full text]
  • Communicable Disease Control in Emergencies: a Field Manual Edited by M
    Communicable disease control in emergencies A field manual Communicable disease control in emergencies A field manual Edited by M.A. Connolly WHO Library Cataloguing-in-Publication Data Communicable disease control in emergencies: a field manual edited by M. A. Connolly. 1.Communicable disease control–methods 2.Emergencies 3.Disease outbreaks–prevention and control 4.Manuals I.Connolly, Máire A. ISBN 92 4 154616 6 (NLM Classification: WA 110) WHO/CDS/2005.27 © World Health Organization, 2005 All rights reserved. The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the pert of the World Health Organization concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. Dotted lines on map represent approximate border lines for which there may not yet be full agreement. The mention of specific companies or of certain manufacturers’ products does not imply that they are endorsed or recommended by the World Health Organization in preference to others of a similar nature that are not mentioned. Errors and omissions excepted, the names of proprietary products are distinguished by initial capital letters. All reasonable precautions have been taken by WHO to verify he information contained in this publication. However, the published material is being distributed without warranty of any kind, either express or implied. The responsibility for the interpretation and use of the material lies with the reader. In no event shall the World Health Organization be liable for damages arising in its use.
    [Show full text]