DOCSLIB.ORG

1 Damped Oscillations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1 Damped Oscillations Physics 106 Lecture 12 Oscillations – II SJ 7th Ed.: Chap 15.4, Read only 15.6 & 15.7 • Recap: SHM using phasors (uniform circular motion) • Phys ica l pendu lum example • Damped harmonic oscillations • Forced oscillations and resonance. • Resonance examples and discussion – music – structural and mechanical engineering – waves • Sample problems • Oscillations summary chart Damped Oscillations • Non-conservative forces may be present – Friction is a common nonconservative force neglect – No longer an ideal system (such as those dealt with gravity so far) • The mechanical energy of the system diminishes in time, motion is said to be damped • The motion of the system can be decaying oscillations if the damping is “weak”. • If damping is “strong”, motion may die away without oscillating. • Still no driving force, once system has been started 1 Add Damping: Emech not constant, oscillations not simple • Spring oscillator as before, but with dissipative force Fdamp neglect such as the system in the figure, with vane moving in fluid. gravity Fdamp viscous drag force, proportional to velocity Fdamp = −bv • Previous force equation gets a new, damping force term d2x(t) dx(t) Fnet = m = − kx()(t) − b dt2 dt new term d2x(t) b dx(t) k + = − x(t) dt2 m dt m Solution for Damped oscillator equation new term d2x(t) b dx(t) k + = − x(t) dt2 m dt m bt − 2 Solution: 2m k b x(t) = xme cos(ω't + φ) ω'≡ − modified m 2 oscillations exponentially altered ω’ can be real 4m decaying envelope frequency or imaginary k ω = : natural frequency 0 m 22 ωω'(/2)≡−0 bm • Recover undamped solution for b Æ 0 2 Damped physical systems can be of three types bt − 2 Solution: 2m k b x(t) = xme cos(ω't + φ) ω'≡ − damped m 4m2 oscillations UdUnder dampe d: small bk< 2 m bk2 < , for which ω is positive. 4mm2 Critically damped: bkm= 2 2 b k 2 ≈ ≡ ω0 for which ω'≈ 0 4m2 m 2 Overdamped: b k 2 > ≡ ω0 for which ω' is imaginary 4m2 m Math Review: cos(ix )==+ cosh( x ) ( exx e− ) / 2 sin(ix )==− sinh( x ) ( exx e− ) / 2 cos(ix+ y )=− cos( ix )cos( y ) sin( ix )sin( y ) Types of Damping, cont (Link to Active Fig.) a) an underdamped oscillator b) a critically damped oscillator c) an overdamped oscillator For critically damped and overdamped oscillators there is no periodic motion and the angular frequency ω has a different meaning 3 b2 k << ≡ ω2 Weakly damped oscillator : 4m2 m 0 bt − kb2 − 2m ω ' ≡≈ω0 xt()= xem cos(ω0 t+ϕ ) m 4m2 bt - 2m Xm = xm()(t) ≈ xme slow decay of amplitude envelope ≈ cos(ω0t + φ) small fractional change in amplitude during one complete cycle b2 k << ≡ ω2 Weakly damped oscillator : 4m2 m 0 bt kb2 − ω ' ≡≈− ω0 xt()= xe2m cos(ω t+ϕ ) m 4m2 m 0 bt - Amplitude : X = A 2m m xm(t) ≈ xme small fractional slow decay change in amplitude of amplitude envelope during one complete cycle ≈ cos(ω0t + φ) Velocity with weak damping: find derivative bt − d 2m maximum velocity v(t) = x(t) ≈ vme sin(ω't + φ) dt vm = − ω0xm altered exponentially frequency ~ ω decaying envelope 0 4 Mechanical energy decays exponentially in an “weakly damped” oscillator (small b) E = K(t) + U(t) = 1 mv2(t) + 1 kx2(t) mech 2 2 bt − 2m xt()=+ xem cos(ω0 t ϕ ) Velocity with weak damping: find derivative bt − d 2m maximum velocity v(t) = x(t) ≈ vme sin(ω't + φ) dt vm = − ω0xm altered exponentially frequency ~ ω decaying envelope 0 bt − ⎛⎞b 2m xem ⎜⎟−+cos(ω0 tϕ ) term is negligible, because b is small.. ⎝⎠2m Mechanical energy decays exponentially in an “weakly damped” oscillator (small b) E = K(t) + U(t) = 1 mv2(t) + 1 kx2(t) mech 2 2 Substitute previous solutions: bt bt − − 2m 2m x(t) = xme cos(ω't + φ) v(t) ≈ −ω0xme sin(ω't + φ) E = 1 mω2x2 e−bt / msin2(ω't + φ) mech 2 0 m + 1 kx2 e−bt / mcos2(ω't + φ) 2 m As always: cos2(x) + sin2(x) = 1 2 k Also: ω ≡ 0 m ∴ E (t) = 1 kx2 e−bt / m mech 2 m exponential decay at twice Initial mechanical energy the rate of amplitude decay 5 Damped physical systems can be of three types bt − 2 Solution: 2m k b x(t) = xme cos(ω't + φ) ω'≡ − damped m 2 exponentially altered ω’ can be real 4m oscillations decaying envelope frequency or imaginary 2 Underdamped: b k 2 << ≡ ω0 for which ω'≈ ω0 4m2 m The restoring force is large compared to the damping force. The system oscillates with decaying amplitude 2 Critically damped: b k 2 ≈ ≡ ω0 for which ω'≈ 0 4m2 m The restoring force and damping force are comparable in effect. The system can not oscillate; the amplitude dies away exponentially 2 Overdamped: b k 2 > ≡ ω0 for which ω' is imaginary 4m2 m The damping force is much stronger than the restoring force. The amplitude dies away as a modified exponential Note: Cos( ix ) = Cosh( x ) Forced (Driven) Oscillations and Resonance An external driving force starts oscillations in a stationary system The amplitude remains constant (or grows) if the energy input per cycle exactly equals (or exceeds) the energy loss from damping Eventually, Edriving = Elost and a steady-state condition is reached Oscillations then continue with constant amplitude Oscillations are at the driving frequency ωD FD(t) = F0 cos(ωDt + φ') FD(t) Oscillating driving force applied to a dampe d osc illat or 6 Equation for Forced (Driven) Oscillations k ω = natural frequency ω = 0 0 m ωD = driving frequency of external force External driving force function: FD(t) = F0 cos(ωDt + φ') dx() t d2 x () t FFt==( ) -b - k x(t) m net D dt dt 2 FD(t) Solution for Forced (Driven) Oscillations dx() t d2 x () t FFt==( ) -b - k x(t) m net D dt dt 2 FD(t) = F0 cos(ωDt + φ') Solution (steady state solution): x(t) = Acos(ωDt + φ) F0 /m where A = 2 2 2 bωD 2 (ωD − ω0 ) + ( ) m FD(t) The system always oscillat es at the driving frequency ωD in steady-state The amplitude A depends on how k ω ω ω = close D is to natural frequency 0 0 m “resonance” 7 Amplitude of the driven oscillations: F /m A = 0 bω (ω2 − ω2 )2 + ( D )2 D 0 m The largest amplitude oscillations occur at or resonance near RESONANCE (ωD ~ ω0) As damping becomes weaker Æ resonance sharpens & amplitude at resonance increases. Resonance At resonance, the applied force is in phase with the velocity and the power Fov transferred to the oscillator is a maximum. The amplit u de o f resonan t oscillations can become enormous when the damping is weak, storing enormous amounts of energy Applications: • buildings driven by earthquakes • bridges under wind load • all kinds of radio devices, microwave • other numerous applications 8 Forced resonant torsional oscillations due to wind - Tacoma Narrows Bridge Roadway collapse - Tacoma Narrows Bridge 9 Twisting bridge at resonance frequency Breaking glass with voice 10.
Load more

Recommended publications
  • “Mechanical Universe and Beyond” Videos—CE Mungan, Spring 2001
    Keywords in “Mechanical Universe and Beyond” Videos—C.E. Mungan, Spring 2001 This entire series can be viewed online at http://www.learner.org/resources/series42.html. Some of the titles below have been modified by me to better reflect their contents. In my opinion, tapes 21–22 are the best in the whole series! 1. Introduction to Classical Mechanics: Kepler, Galileo, Newton 2. Falling Bodies: s = gt2 / 2, ! = gt, a = g 3. Differentiation: introductory math 4. Inertia: Newton’s first law, Copernican solar system 5. Vectors: quaternions, unit vectors, dot and cross products 6. Newton’s Laws: Newton’s second law, momentum, Newton’s third law, monkey-gun demo 7. Integration: Newton vs. Leibniz, anti-derivatives 8. Gravity: planetary orbits, universal law of gravity, the Moon falls toward the Earth 9. UCM: Ptolemaic solar system, centripetal acceleration and force 10. Fundamental Forces: Cavendish experiment, Franklin, unified theory, viscosity, tandem accelerator 11. Gravity and E&M: fundamental constants, speed of light, Oersted experiment, Maxwell 12. Millikan Experiment: CRT, scientific method 13. Energy Conservation: work, gravitational PE, KE, mechanical energy, heat, Joule, microscopic forms of energy, useful available energy 14. PE: stability, conservation, position dependence, escape speed 15. Conservation of Linear Momentum: Descartes, generalized Newton’s second law, Earth- Moon system, linear accelerator 16. SHM: amplitude-independent period of pendulum, timekeeping, restoring force, connection to UCM, elastic PE 17. Resonance: Tacoma Narrows, music, breaking wineglass demo, earthquakes, Aeolian harp, vortex shedding 18. Waves: shock waves, speed of sound, coupled oscillators, wave properties, gravity waves, isothermal vs. adiabatic bulk modulus 19. Conservation of Angular Momentum: Kepler’s second law, vortices, torque, Brahe 20.
    [Show full text]
  • 14 Mass on a Spring and Other Systems Described by Linear ODE
    14 Mass on a spring and other systems described by linear ODE 14.1 Mass on a spring Consider a mass hanging on a spring (see the figure). The position of the mass in uniquely defined by one coordinate x(t) along the x-axis, whose direction is chosen to be along the direction of the force of gravity. Note that if this mass is in an equilibrium, then the string is stretched, say by amount s units. The origin of x-axis is taken that point of the mass at rest. Figure 1: Mechanical system “mass on a spring” We know that the movement of the mass is determined by the second Newton’s law, that can be stated (for our particular one-dimensional case) as ma = Fi, X where m is the mass of the object, a is the acceleration, which, as we know from Calculus, is the second derivative of the displacement x(t), a =x ¨, and Fi is the net force applied. What we know about the net force? This has to include the gravity, of course: F1 = mg, where g is the acceleration 2 P due to gravity (g 9.8 m/s in metric units). The restoring force of the spring is governed by Hooke’s ≈ law, which says that the restoring force in the opposite to the movement direction is proportional to the distance stretched: F2 = k(s + x), here minus signifies that the force is acting in the opposite − direction, and the distance stretched also includes s units. Note that at the equilibrium (i.e., when x = 0) and absence of other forces we have F1 + F2 = 0 and hence mg ks = 0 (this last expression − often allows to find the spring constant k given the amount of s the spring is stretched by the mass m).
    [Show full text]
  • Caltech News
    Volume 16, No.7, December 1982 CALTECH NEWS pounds, became optional and were Three Caltech offered in the winter and spring. graduate programs But under this plan, there was an overlap in material that diluted the rank number one program's efficiency, blending per­ in nationwide survey sons in the same classrooms whose backgrounds varied widely. Some Caltech ranked number one - students took 3B and 3C before either alone or with other institutions proceeding on to 46A and 46B, - in a recent report that judged the which focused on organic systems, scholastic quality of graduate pro" while other students went directly grams in mathematics and science at into the organic program. the nation's major research Another matter to be addressed universities. stemmed from the fact that, across Caltech led the field in geoscience, the country, the lines between inor­ and shared top rankings with Har­ ganic and organic chemistry had ' vard in physics. The Institute was in become increasingly blurred. Explains a four-way tie for first in chemistry Professor of Chemistry Peter Der­ with Berkeley, Harvard, and MIT. van, "We use common analytical The report was the result of a equipment. We are both molecule two-year, $500,000 study published builders in our efforts to invent new under the sponsorship of four aca­ materials. We use common bonds for demic groups - the American Coun­ The Mead Laboratory is the setting for Chemistry 5, where Carlotta Paulsen uses a rotary probing how chemical bonds are evaporator to remove a solvent from a synthesized product. Paulsen is a junior majoring in made and broken." cil of Learned Societies, the American chemistry.
    [Show full text]
  • Nuclear Magnetic Resonance and Its Application in Condensed Matter Physics
    Nuclear Magnetic Resonance and Its Application in Condensed Matter Physics Kangbo Hao 1. Introduction Nuclear Magnetic Resonance (NMR) is a physics phenomenon first observed by Isidor Rabi in 1938. [1] Since then, the NMR spectroscopy has been applied in a wide range of areas such as physics, chemistry, and medical examination. In this paper, I want to briefly discuss about the theory of NMR spectroscopy and its recent application in condensed matter physics. 2. Principles of NMR NMR occurs when some certain nuclei are in a static magnetic field and another oscillation magnetic field. Assuming a nucleus has a spin angular momentum 퐼⃗ = ℏ푚퐼, then its magnetic moment 휇⃗ is 휇⃗ = 훾퐼⃗ (1) The 훾 here is the gyromagnetic ratio, which depends on the property of the nucleus. If we put such a nucleus in a static magnetic field 퐵⃗⃗0, then the magnetic moment of this nuclei will process about this magnetic field. Therefore we have, [2] [3] 푑퐼⃗ 1 푑휇⃗⃗⃗ 휏⃗ = 휇⃗ × 퐵⃗⃗ = = (2) 0 푑푥 훾 푑푥 From this semiclassical picture, we can easily derive that the precession frequency 휔0 (which is called the Larmor angular frequency) is 휔0 = 훾퐵0 (3) Then, if another small oscillating magnetic field is added to the plane perpendicular to 퐵⃗⃗0, then the total magnetic field is (Assuming 퐵⃗⃗0 is in 푧̂ direction) 퐵⃗⃗ = 퐵0푧̂ + 퐵1(cos(휔푡) 푥̂ + sin(휔푡) 푦̂) (4) If we choose a frame (푥̂′, 푦̂′, 푧̂′ = 푧̂) rotating with the oscillating magnetic field, then the effective magnetic field in this frame is 휔 퐵̂ = (퐵 − ) 푧̂ + 퐵 푥̂′ (5) 푒푓푓 0 훾 1 As a result, at 휔 = 훾퐵0, which is the resonant frequency, the 푧̂ component will vanish, and thus the spin angular momentum will precess about 퐵⃗⃗1 instead.
    [Show full text]
  • Vibration and Sound Damping in Polymers
    GENERAL ARTICLE Vibration and Sound Damping in Polymers V G Geethamma, R Asaletha, Nandakumar Kalarikkal and Sabu Thomas Excessive vibrations or loud sounds cause deafness or reduced efficiency of people, wastage of energy and fatigue failure of machines/structures. Hence, unwanted vibrations need to be dampened. This article describes the transmis- sion of vibrations/sound through different materials such as metals and polymers. Viscoelasticity and glass transition are two important factors which influence the vibration damping of polymers. Among polymers, rubbers exhibit greater damping capability compared to plastics. Rubbers 1 V G Geethamma is at the reduce vibration and sound whereas metals radiate sound. Mahatma Gandhi Univer- sity, Kerala. Her research The damping property of rubbers is utilized in products like interests include plastics vibration damper, shock absorber, bridge bearing, seismic and rubber composites, and soft lithograpy. absorber, etc. 2R Asaletha is at the Cochin University of Sound is created by the pressure fluctuations in the medium due Science and Technology. to vibration (oscillation) of an object. Vibration is a desirable Her research topic is NR/PS blend- phenomenon as it originates sound. But, continuous vibration is compatibilization studies. harmful to machines and structures since it results in wastage of 3Nandakumar Kalarikkal is energy and causes fatigue failure. Sometimes vibration is a at the Mahatma Gandhi nuisance as it creates noise, and exposure to loud sound causes University, Kerala. His research interests include deafness or reduced efficiency of people. So it is essential to nonlinear optics, synthesis, reduce excessive vibrations and sound. characterization and applications of nano- multiferroics, nano- We can imagine how noisy and irritating it would be to pull a steel semiconductors, nano- chair along the floor.
    [Show full text]
  • Simple Harmonic Motion
    [SHIVOK SP211] October 30, 2015 CH 15 Simple Harmonic Motion I. Oscillatory motion A. Motion which is periodic in time, that is, motion that repeats itself in time. B. Examples: 1. Power line oscillates when the wind blows past it 2. Earthquake oscillations move buildings C. Sometimes the oscillations are so severe, that the system exhibiting oscillations break apart. 1. Tacoma Narrows Bridge Collapse "Gallopin' Gertie" a) http://www.youtube.com/watch?v=j‐zczJXSxnw II. Simple Harmonic Motion A. http://www.youtube.com/watch?v=__2YND93ofE Watch the video in your spare time. This professor is my teaching Idol. B. In the figure below snapshots of a simple oscillatory system is shown. A particle repeatedly moves back and forth about the point x=0. Page 1 [SHIVOK SP211] October 30, 2015 C. The time taken for one complete oscillation is the period, T. In the time of one T, the system travels from x=+x , to –x , and then back to m m its original position x . m D. The velocity vector arrows are scaled to indicate the magnitude of the speed of the system at different times. At x=±x , the velocity is m zero. E. Frequency of oscillation is the number of oscillations that are completed in each second. 1. The symbol for frequency is f, and the SI unit is the hertz (abbreviated as Hz). 2. It follows that F. Any motion that repeats itself is periodic or harmonic. G. If the motion is a sinusoidal function of time, it is called simple harmonic motion (SHM).
    [Show full text]
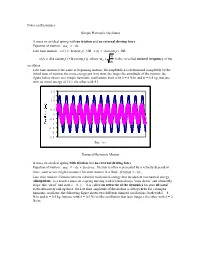
  • Notes on Resonance Simple Harmonic Oscillator • a Mass on An
    Notes on Resonance Simple Harmonic Oscillator · A mass on an ideal spring with no friction and no external driving force · Equation of motion: max = - kx · Late time motion: x(t) = Asin(w0 t) OR x(t) = Acos(w0 t) OR k x(t) = A(a sin(w t) + b cos(w t)), where w = is the so-called natural frequency of the 0 0 0 m oscillator · Late time motion is the same as beginning motion; the amplitude A is determined completely by the initial state of motion; the more energy put in to start, the larger the amplitude of the motion; the figure below shows two simple harmonic oscillations, both with k = 8 N/m and m = 0.5 kg, but one with an initial energy of 16 J, the other with 4 J. 2.5 2 1.5 1 0.5 0 -0.5 0 5 10 15 20 -1 -1.5 -2 -2.5 Time (s) Damped Harmonic Motion · A mass on an ideal spring with friction, but no external driving force · Equation of motion: max = - kx + friction; friction is often represented by a velocity dependent force, such as one might encounter for slow motion in a fluid: friction = - bv x · Late time motion: friction converts coherent mechanical energy into incoherent mechanical energy (dissipation); as a result a mass on a spring moving with friction always “runs down” and ultimately stops; this “dead” end state x = 0, vx = 0 is called an attractor of the dynamics because all initial states ultimately end up there; the late time amplitude of the motion is always zero for a damped harmonic oscillator; the following figure shows two different damped oscillations, both with k = 8 N/m and m = 0.5 kg, but one with b = 0.5 Ns/m (the oscillation that lasts longer), the other with b = 2 Ns/m.
    [Show full text]
  • Condensed Matter Physics Experiments List 1
    Physics 431: Modern Physics Laboratory – Condensed Matter Physics Experiments The Oscilloscope and Function Generator Exercise. This ungraded exercise allows students to learn about oscilloscopes and function generators. Students measure digital and analog signals of different frequencies and amplitudes, explore how triggering works, and learn about the signal averaging and analysis features of digital scopes. They also explore the consequences of finite input impedance of the scope and and output impedance of the generator. List 1 Electron Charge and Boltzmann Constants from Johnson Noise and Shot Noise Mea- surements. Because electronic noise is an intrinsic characteristic of electronic components and circuits, it is related to fundamental constants and can be used to measure them. The Johnson (thermal) noise across a resistor is amplified and measured at both room temperature and liquid nitrogen temperature for a series of different resistances. The amplifier contribution to the mea- sured noise is subtracted out and the dependence of the noise voltage on the value of the resistance leads to the value of the Boltzmann constant kB. In shot noise, a series of different currents are passed through a vacuum diode and the RMS noise across a load resistor is measured at each current. Since the current is carried by electron-size charges, the shot noise measurements contain information about the magnitude of the elementary charge e. The experiment also introduces the concept of “noise figure” of an amplifier and gives students experience with a FFT signal analyzer. Hall Effect in Conductors and Semiconductors. The classical Hall effect is the basis of most sensors used in magnetic field measurements.
    [Show full text]
  • AN826 Crystal Oscillator Basics and Crystal Selection for Rfpic™ And
    AN826 Crystal Oscillator Basics and Crystal Selection for rfPICTM and PICmicro® Devices • What temperature stability is needed? Author: Steven Bible Microchip Technology Inc. • What temperature range will be required? • Which enclosure (holder) do you desire? INTRODUCTION • What load capacitance (CL) do you require? • What shunt capacitance (C ) do you require? Oscillators are an important component of radio fre- 0 quency (RF) and digital devices. Today, product design • Is pullability required? engineers often do not find themselves designing oscil- • What motional capacitance (C1) do you require? lators because the oscillator circuitry is provided on the • What Equivalent Series Resistance (ESR) is device. However, the circuitry is not complete. Selec- required? tion of the crystal and external capacitors have been • What drive level is required? left to the product design engineer. If the incorrect crys- To the uninitiated, these are overwhelming questions. tal and external capacitors are selected, it can lead to a What effect do these specifications have on the opera- product that does not operate properly, fails prema- tion of the oscillator? What do they mean? It becomes turely, or will not operate over the intended temperature apparent to the product design engineer that the only range. For product success it is important that the way to answer these questions is to understand how an designer understand how an oscillator operates in oscillator works. order to select the correct crystal. This Application Note will not make you into an oscilla- Selection of a crystal appears deceivingly simple. Take tor designer. It will only explain the operation of an for example the case of a microcontroller.
    [Show full text]
  • Chapter 10: Elasticity and Oscillations
    Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2.
    [Show full text]
  • Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
    Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time.
    [Show full text]
  • Notes on the Critically Damped Harmonic Oscillator Physics 2BL - David Kleinfeld
    Notes on the Critically Damped Harmonic Oscillator Physics 2BL - David Kleinfeld We often have to build an electrical or mechanical device. An understand- ing of physics may help in the design and tuning of such a device. Here, we consider a critically damped spring oscillator as a model design for the shock absorber of a car. We consider a mass, denoted m, that is connected to a spring with spring constant k, so that the restoring force is F =-kx, and which moves in a lossy manner so that the frictional force is F =-bv =-bx˙. Prof. Newton tells us that F = mx¨ = −kx − bx˙ (1) Thus k b x¨ + x + x˙ = 0 (2) m m The two reduced constants are the natural frequency k ω = (3) 0 m and the decay constant b α = (4) m so that we need to consider 2 x¨ + ω0x + αx˙ = 0 (5) The above equation describes simple harmonic motion with loss. It is dis- cussed in lots of text books, but I want to consider a formulation of the solution that is most natural for critical damping. We know that when the damping constant is zero, i.e., α = 0, the solution 2 ofx ¨ + ω0x = 0 is given by: − x(t)=Ae+iω0t + Be iω0t (6) where A and B are constants that are found from the initial conditions, i.e., x(0) andx ˙(0). In a nut shell, the system oscillates forever. 1 We know that when the the natural frequency is zero, i.e., ω0 = 0, the solution ofx ¨ + αx˙ = 0 is given by: x˙(t)=Ae−αt (7) and 1 − e−αt x(t)=A + B (8) α where A and B are constants that are found from the initial conditions.
    [Show full text]