Restricted Structural Change and the Unit Root Hypothesis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Beirut Divided: the Potential of Urban Design in Reuniting a Culturally Divided City
The Bartlett Development Planning Unit DPU WORKING PAPER NO. 153 Beirut Divided: The potential of urban design in reuniting a culturally divided city Benjamin J Leclair-Paquet DPU Working Papers are downloadable at: www.bartlett.ucl.ac.uk/dpu/latest/ publications/dpu-papers If a hard copy is required, please contact the De- velopment Planning Unit (DPU) at the address at the bottom of the page. Institutions, organisations and booksellers should supply a Purchase Order when ordering Working Papers. Where multiple copies are or- dered, and the cost of postage and package is significant, the DPU may make a charge to cov- er costs. DPU Working Papers provide an outlet for researchers and professionals working in the fields of development, environment, urban and regional development, and planning. They report on work in progress, with the aim to dissemi- nate ideas and initiate discussion. Comments and correspondence are welcomed by authors and should be sent to them, c/o The Editor, DPU Working Papers. Copyright of a DPU Working Paper lies with the author and there are no restrictions on it being published elsewhere in any version or form. DPU Working Papers are refereed by DPU academic staff and/or DPU Associates before selection for publication. Texts should be submitted to the DPU Working Papers' Editors, Dr Camillo Boano and Dr Barbara Lipietz. Graphics and layout: Giorgio Talocci, Camila Cociña and Luz Navarro The Bartlett Development Planning Unit | The Bartlett | University College London 34 Tavistock Square - London - WC1H 9EZ Tel: +44 (0)20 7679 1111 - Fax: +44 (0)20 7679 1112 - www.bartlett.ucl.ac.uk/dpu DPU WORKING PAPER NO. -

Craig-Cvd506-Manual.Pdf
.BJOUFOBODFBOE$BSF $BSJOHGPSUIF6OJU *ODMJOBUJPO ti5IFBQQBSBUVTTIBMMOPUCFFYQPTFEUPESJQQJOHPS t%POPUJOTUBMMUIFVOJUJOBOJODMJOFEQPTJUJPO*UJTEFTJHOFE TQMBTIJOHwBOEUIBUOPPCKFDUTGJMMFEXJUIMJRVJETIBMM UPCFPQFSBUFEJOBIPSJ[POUBMQPTJUJPOPOMZ CFQMBDFEPOUIFVOJU t*GBOZUIJOHGBMMTJOUPUIFDBCJOFU VOQMVHUIFVOJUBOEIBWF "WPJE*OUFSGFSFODF JUDIFDLFECZRVBMJGJFEQFSTPOOFMCFGPSFPQFSBUJOHJUBOZ t8IFOZPVQMBDFUIJTVOJUOFBS57 SBEJPPS7$3 UIFQJDUVSF GVSUIFS NBZCFDPNFQPPSBOEUIFTPVOENBZCFEJTUPSUFE*OUIJT DBTF NPWFUIFVOJUBXBZGSPNUIF57 SBEJPPS7$3 $MFBOJOHUIF6OJU t5PQSFWFOUGJSFPSTIPDLIB[BSE EJTDPOOFDUZPVSVOJUGSPN %JTDPOOFDU1PXFS UIF"$QPXFSTPVSDFXIFODMFBOJOH t*GZPVBSFOPUHPJOHUPVTFUIFVOJUGPSBMPOHUJNF CF t5IFGJOJTIPOZPVSVOJUNBZCFDMFBOFEXJUIBEVTUDMPUI TVSFUPEJTDPOOFDUUIFVOJUGSPNUIFXBMMPVUMFU5P BOEDBSFEGPSBTPUIFSGVSOJUVSF EJTDPOOFDUUIF"$QPXFSDPSE NBJOMFBET HSBTQUIFQMVH 6TFDBVUJPOXIFODMFBOJOHBOEXJQJOHUIFQMBTUJDQBSUT JUTFMG OFWFSQVMMUIFDPSE t.JMETPBQBOEBEBNQDMPUINBZCFVTFEPOUIFGSPOUQBOFM *.1035"/54"'&5:*/4536$5*0/4 8BSOJOH5PSFEVDFUIFSJTLPGGJSFPSFMFDUSJDTIPDL EPOPU #FGPSFVTJOHUIFVOJU CFTVSFUPSFBEBMMPQFSBUJOH FYQPTFUIJTBQQMJBODFUPSBJOPSNPJTUVSF JOTUSVDUJPOTDBSFGVMMZ1MFBTFOPUFUIBUUIFTFBSFHFOFSBM %BOHFSPVTIJHIWPMUBHFTBSFQSFTFOUJOTJEFUIF QSFDBVUJPOTBOENBZOPUQFSUBJOUPZPVSVOJU'PSFYBNQMF FODMPTVSF%POPUPQFOUIFDBCJOFU SFGFSTFSWJDJOH UIJTVOJUNBZOPUIBWFUIFDBQBCJMJUZUPCFDPOOFDUFEUPBO UPRVBMJGJFEQFSTPOOFMPOMZ PVUEPPSBOUFOOB 3FBEUIFTFJOTUSVDUJPOT "MMUIFTBGFUZBOEPQFSBUJOHJOTUSVDUJPOTTIPVMECFSFBE CFGPSFUIFQSPEVDUJTPQFSBUFE ,FFQUIFTFJOTUSVDUJPOT 5IFTBGFUZBOEPQFSBUJOHJOTUSVDUJPOTTIPVMECFSFUBJOFE GPSGVUVSFSFGFSFODF -
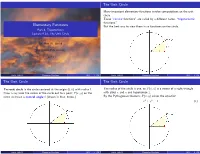
4.1 Unit Circle Cosine & Sine (Slides 4-To-1).Pdf
The Unit Circle Many important elementary functions involve computations on the unit circle. These \circular functions" are called by a different name, \trigonometric functions." Elementary Functions But the best way to view them is as functions on the circle. Part 4, Trigonometry Lecture 4.1a, The Unit Circle Dr. Ken W. Smith Sam Houston State University 2013 Smith (SHSU) Elementary Functions 2013 1 / 54 Smith (SHSU) Elementary Functions 2013 2 / 54 The Unit Circle The Unit Circle The unit circle is the circle centered at the origin (0; 0) with radius 1. The radius of the circle is one, so P (x; y) is a vertex of a right triangle Draw a ray from the center of the circle out to a point P (x; y) on the with sides x and y and hypotenuse 1. circle to create a central angle θ (drawn in blue, below.) By the Pythagorean theorem, P (x; y) solves the equation x2 + y2 = 1 (1) Smith (SHSU) Elementary Functions 2013 3 / 54 Smith (SHSU) Elementary Functions 2013 4 / 54 Central Angles and Arcs Central Angles and Arcs An arc of the circle corresponds to a central angle created by drawing line segments from the endpoints of the arc to the center. The Babylonians (4000 years ago!) divided the circle into 360 pieces, called degrees. This choice is a very human one; it does not have a natural mathematical reason. (It is not \intrinsic" to the circle.) The most natural way to measure arcs on a circle is by the intrinsic unit of measurement which comes with the circle, that is, the length of the radius. -

CINE MEJOR ACTOR JEFF BRIDGES / Bad Blake
CINE MEJOR ACTOR JEFF BRIDGES / Bad Blake - "CRAZY HEART" (Fox Searchlight Pictures) GEORGE CLOONEY / Ryan Bingham - "UP IN THE AIR" (Paramount Pictures) COLIN FIRTH / George Falconer - "A SINGLE MAN" (The Weinstein Company) MORGAN FREEMAN / Nelson Mandela - "INVICTUS" (Warner Bros. Pictures) JEREMY RENNER / Staff Sgt. William James - "THE HURT LOCKER" (Summit Entertainment) MEJOR ACTRIZ SANDRA BULLOCK / Leigh Anne Tuohy - "THE BLIND SIDE" (Warner Bros. Pictures) HELEN MIRREN / Sofya - "THE LAST STATION" (Sony Pictures Classics) CAREY MULLIGAN / Jenny - "AN EDUCATION" (Sony Pictures Classics) GABOUREY SIDIBE / Precious - "PRECIOUS: BASED ON THE NOVEL ‘PUSH’ BY SAPPHIRE" (Lionsgate) MERYL STREEP / Julia Child - "JULIE & JULIA" (Columbia Pictures) MEJOR ACTOR DE REPARTO MATT DAMON / Francois Pienaar - "INVICTUS" (Warner Bros. Pictures) WOODY HARRELSON / Captain Tony Stone - "THE MESSENGER" (Oscilloscope Laboratories) CHRISTOPHER PLUMMER / Tolstoy - "THE LAST STATION" (Sony Pictures Classics) STANLEY TUCCI / George Harvey - "THE LOVELY BONES" (Paramount Pictures) CHRISTOPH WALTZ / Col. Hans Landa - "INGLOURIOUS BASTERDS" (The Weinstein Company/Universal Pictures) MEJOR ACTRIZ DE REPARTO PENÉLOPE CRUZ / Carla - "NINE" (The Weinstein Company) VERA FARMIGA / Alex Goran - "UP IN THE AIR" (Paramount Pictures) ANNA KENDRICK / Natalie Keener - "UP IN THE AIR" (Paramount Pictures) DIANE KRUGER / Bridget Von Hammersmark - "INGLOURIOUS BASTERDS" (The Weinstein Company/Universal Pictures) MO’NIQUE / Mary - "PRECIOUS: BASED ON THE NOVEL ‘PUSH’ BY SAPPHIRE" (Lionsgate) MEJOR ELENCO AN EDUCATION (Sony Pictures Classics) DOMINIC COOPER / Danny ALFRED MOLINA / Jack CAREY MULLIGAN / Jenny ROSAMUND PIKE / Helen PETER SARSGAARD / David EMMA THOMPSON / Headmistress OLIVIA WILLIAMS / Miss Stubbs THE HURT LOCKER (Summit Entertainment) CHRISTIAN CAMARGO / Col. John Cambridge BRIAN GERAGHTY / Specialist Owen Eldridge EVANGELINE LILLY / Connie James ANTHONY MACKIE / Sgt. J.T. -

THE INVISIBLE THEATRE John Amos
PRESS RELEASE Contact: Cathy Johnson or Susan Claassen 1400 N. First Ave, Tucson, AZ. 85719 Administration – (520) 884-0672 Box Office – (520) 882-9721 [email protected] www.invisibletheatre.com FOR RELEASE ON OR AFTER DECEMBER 26, 2011 THE INVISIBLE THEATRE Presents Written by and Starring John Amos Directed and Designed by John Harris, Jr. Made possible in part through the generous support of Dr. Vivian Cox, David Hendricks and Dee-Dee Samet WHERE: The Berger Performing Arts Center 1200 W. Speedway Blvd. Tucson, AZ 85745 WHEN: January 14, 2012 at 8:00 pm and January 15, 2012 at 3:00 pm TICKETS: Ticket Price: $42 To charge tickets by phone, call (520) 882-9721 To purchase tickets on-line, go to www.invisibletheatre.com and click on the OvationTix logo Discounts available for groups of ten or more RUNNING TIME : 2 hours with an intermission Tucson, Arizona (December 26, 2011); You know him from his Emmy Award nominated performance as the heroic adult Kunta Kinte in the ground breaking mini-series Roots , or as James Evans, the indestructible father from the hit television sitcom Good Times . You were delighted by his hilarious performance opposite Eddie Murphy in the box office blockbuster Coming to America . You have enjoyed him on the Emmy Award-winning drama The West Wing , the CBS series The District, Fresh Prince of Bel-Air and House . Whether he was performing with Sylvester Stallone in Lock Up or co-starring with Bruce Willis in Die Hard II , John Amos has always delivered outstanding performances. He now presents yet another astonishing character portrayal in his own extraordinary creation, John Amos’ HALLEY’S COMET where he takes the audience on a whirlwind adventure back in time, beginning at the turn of the century when the world was full of dreams and promises of wonderful things to come. -

Geospatial Analysis of Terrorist Activities
The author(s) shown below used Federal funds provided by the U.S. Department of Justice and prepared the following final report: Document Title: Geospatial Analysis of Terrorist Activities: The Identification of Spatial and Temporal Patterns of Preparatory Behavior of International and Environmental Terrorists Author: Brent L. Smith ; Jackson Cothren ; Paxton Roberts ; Kelly R. Damphousse Document No.: 222909 Date Received: May 2008 Award Number: 2005-IJ-CX-0200 This report has not been published by the U.S. Department of Justice. To provide better customer service, NCJRS has made this Federally- funded grant final report available electronically in addition to traditional paper copies. Opinions or points of view expressed are those of the author(s) and do not necessarily reflect the official position or policies of the U.S. Department of Justice. University of Arkansas NIJ Grant 2005-IJ-CX-0200 Geospatial Analysis of Terrorist Activities: The Identification of Spatial and Temporal Patterns of Preparatory Behavior of International and Environmental Terrorists Brent L. Smith Terrorism Research Center in Fulbright College University of Arkansas Jackson Cothren Center for Advanced Spatial Technologies University of Arkansas Paxton Roberts Terrorism Research Center in Fulbright College University of Arkansas Kelly R. Damphousse KayTen Research and Development, Inc. February 2008 http://trc.uark.edu Terrorism Research Center in Fulbright College University of Arkansas TABLE OF CONTENTS Page Number Table of Contents............................................................................................................... -

Notice Is Hereby Given That Bids Will Be Received by the Unit Manager, ATLANTA MANAGEMENT UNIT, for Certain Timber on the Following Described Lands
DEPARTMENT OF NATURAL RESOURCES STATE OF MICHIGAN TIMBER SALE PROSPECTUS #5298 SCHEDULED SALE DATE AND TIME: 10:00 a.m. (local time) on January 27, 2015. LOCATION: ATLANTA MGMT UNIT, 13501 M-33, ATLANTA, MI 49709. PROSPECTUS NOTE: The bidder is advised to inspect the sale area and review the location, estimated volumes, operating costs and contract terms of proposed sales. Please be aware that some landowners may request 60 days or more notice for access across their land. Notice is hereby given that bids will be received by the Unit Manager, ATLANTA MANAGEMENT UNIT, for certain timber on the following described lands: SIRLOIN MIX (54-018-14-01) / T33N, R02E, SEC. 28, SWSW. T33N, R02E, SEC. 29, E/2NE, E/2SE, NWSE. T33N, R02E, SEC. 33, W/2NW, W/2SW. Presque Isle County, Advertised Price $46,163.40, 151.0 Acres SALE NOTE: A recreation site such as a trail, pathway, or campground is within the sale area or the vicinity. Certain restrictions/specifications may be applicable including time restrictions. DELMONICO RED PINE (54-025-14-01) / T33N, R02E, SEC. 31, NENE. T33N, R02E, SEC. 32, NWNW. Presque Isle County, Advertised Price $25,511.20, 38.0 Acres RIB RACK MIX (54-045-14-01) / T33N, R02E, SEC. 32, N/2NE, SENE, E/2SW, SE/4. T33N, R02E, SEC. 33, SWSW. Presque Isle County, Advertised Price $48,468.60, 165.0 Acres SALE NOTE: A recreation site such as a trail, pathway, or campground is within the sale area or the vicinity. Certain restrictions/specifications may be applicable including time restrictions. -

Action Against Terrorism Unit
Transnational Threats Department Action against Terrorism Unit Organization for Security and Co-operation in Europe Who we are The Action against Terrorism OSCE-wide Counter-Terrorism Unit of the OSCE Transnational Conference Threats Department supports the In co-operation with the OSCE international and regional Chairmanship, the Unit organizes organizations, civil society, youth OSCE’s 57 participating States the OSCE-wide Counter-Terrorism and the private sector to examine Conference, which brings together emerging threats and explore ways and 11 Partners for Co-operation high-level representatives, counter- to counter and prevent terrorism at terrorism experts and practitioners, local, regional and global levels. in the implementation of their anti-terrorism commitments. Anti-terrorist activities play Based on the OSCE’s a prominent role in the comprehensive and co- OSCE’s overall efforts to operative approach, the Unit address transnational threats. promotes multi-stakeholder Guided by the ‘Consolidated dialogue, raises awareness and Framework for the Fight carries out capacity building to against Terrorism’, the Unit prevent and counter terrorism acts as the OSCE focal by working closely with the point, information resource, Organization’s field presences and implementation partner, and executive structures. providing OSCE participating States and Partners for Co- The Unit collaborates with operation with a wide range international and other regional of programmes and activities. organizations and promotes public-private partnerships -

Download Cryomed Maintenance
UNIVERSITY OF ROCHESTER MEDICAL CENTER HIC-4-0010 Human Immunology Center Core Laboratory David H. Smith Center for Vaccine Biology and Immunology Aab Institute of Biomedical Sciences STANDARD OPERATING PROCEDURE: Operation and Maintenance of the CBS V2300 LN2 Storage Unit with attached liquid nitrogen tank. Date: 02/21/07 Author: Shelley Secor-Socha Approval: Dr. Sally Quataert 1. Purpose/Scope: The purpose of this procedure is to outline the operation and maintenance of the LN2 storage unit with attached liquid nitrogen tank located in the Human Immunology Core Laboratory (HIC). 2. General Policy: The HIC will adhere to the specific guidelines recommended by the manufacture for the use and maintenance of the LN2 storage unit with attached liquid nitrogen tank. The specific policy will be outline below for use and care of the LN2 storage unit with attached liquid nitrogen tank. This will also include the proper documentation indicating that the maintenance recommended has been completed and also tracking of any issues or problems with the LN2 storage unit with attached liquid nitrogen tank on the maintenance log worksheet. 3. General Safety Guidelines 3.1. BSL2 safety equipment and cryoprotectant gloves must be worn; do not touch metal with hands unless wearing cryo gloves. 3.2. LN2 tanks must be chained to wall supports 4. Specific Policy 4.1. Installation of the LN2 storage unit with attached liquid nitrogen tank 4.1.1. Reference the set-up and technical manual for the specific installation procedure of the LN2 storage unit with attached liquid nitrogen tank. 4.1.1.1.Clean the inside and outside of the unit to remove any debris with a clean cloth. -

Canadian Political Science and Medicare: Six Decades of Inquiry Science Politique Et Assurance Maladie Au Canada : Soixante Ans D’Enquête
research paper Canadian Political Science and Medicare: Six Decades of Inquiry Science politique et assurance maladie au Canada : soixante ans d’enquête mCHAELI A. O’ NEILL , PHd Institute on Governance Ottawa, ON dYL AN mCGuINTY, BA, mA Department of Philosophy, Faculty of Arts University of Ottawa Ottawa, ON B TRYAN EskEY, BA Common Law Section, Faculty of Law University of Ottawa Ottawa, ON Abstract Based on an extensive sample of the literature, this critical review dissects the principal themes that have animated the Canadian political science profession on the topic of medicare. The review considers the coincidence of economic eras and how these are reflected in the meth- odological approaches to the study of medicare. As is to be expected, most of the scholarly activity coincides with the economic era marked by fiscal restraint and decreases in social investments (1993–2003). At the same time, the review notes the prevalence of institutional- ism as an approach to the topic and the scholarly community’s near-consensus on medicare as a defining characteristic of the country and its people. HEALTHCARE POLICY Vol.6 No.4, 2011 [49] Michael A. O’Neill et al. Résumé Cette revue critique, fondée sur un vaste échantillon de la littérature, examine les principaux thèmes qui ont stimulé la science politique au Canada en matière d’assurance maladie. La revue tient compte de la coïncidence des périodes économiques et de la façon dont elles sont reflétées dans les démarches méthodologiques pour l’étude de l’assurance maladie. Tel que pressenti, la plupart des activités des chercheurs coïncident avec la période économique marquée par les restrictions budgétaires et les coupures dans l’investissement social (1993-2003). -

No. 3827 UNITED NATIONS
No. 3827 UNITED NATIONS and LEBANON Exchange of letters constituting a provisional arrangement concerning the United Nations Emergency Force Leave Centre in Lebanon. Beirut, 20 and 29 April and 1 May 1957 Official text: English. Registered ex officio on 1 May 1957. ORGANISATION DES NATIONS UNIES et LIBAN change de lettres constituant un accord provisoire con cernant le Centre de permissionnaires de la Force d©urgence des Nations Unies au Liban. Beyrouth, 20 et 29 avril et Ier mai 1957 Texte officiel anglais. Enregistré d'office le 1" mai 1957. 126 United Nations — Treaty Series 1957 No. 3827. EXCHANGE OF LETTERS CONSTITUTING A PROVISIONAL ARRANGEMENT1 BETWEEN THE UNIT ED NATIONS AND LEBANON CONCERNING THE UNITED NATIONS EMERGENCY FORCE LEAVE CEN TRE IN LEBANON. BEIRUT, 20 AND 29 APRIL AND 1 MAY 1957 Beirut, 20 April 1957 Sir, I have the honour to refer to the establishment of the United Nations Emergency Force as an organ of the General Assembly of the United Nations constituted in accordance with Article 22 of the Charter. I would likewise refer to the consent which your Government has generously accorded for the creation in the Lebanon of a Leave Centre, which is considered necessary for the maintenance of the morale and continued efficient operation of the Force, particularly in view of the rigorous and difficult conditions under which its members are serving. Having in mind Article 105 of the Charter which provides that the United Nations shall enjoy in the territory of its Members such privileges and immunities as are necessary for the fulfillment of its purposes, the accession by Lebanon to the Convention on the Privileges and Immunities of the United Nations,2 and the resolutions of the General Assembly providing for the United Nations Emergency Force,3 I should like to propose the following arrangements with a view to enabling the effective fulfillment of the purposes of such a Leave Centre. -

Sergeant First Class Terry OP Wallace
Regular Session, 2007 ENROLLED SENATE RESOLUTION NO. 38 BY SENATORS MARIONNEAUX, ADLEY, AMEDEE, BAJOIE, BARHAM, BOASSO, BROOME, CAIN, CASSIDY, CHAISSON, CHEEK, CRAVINS, DUPLESSIS, DUPRE, ELLINGTON, FIELDS, FONTENOT, B. GAUTREAUX, N. GAUTREAUX, HEITMEIER, HINES, HOLLIS, JACKSON, JONES, KOSTELKA, LENTINI, MALONE, MCPHERSON, MICHOT, MOUNT, MURRAY, NEVERS, QUINN, ROMERO, SCHEDLER, SHEPHERD, SMITH, THEUNISSEN AND ULLO A RESOLUTION To express the sincere and heartfelt condolences of the Senate of the Legislature of Louisiana to the family and loved ones of United States Army Sergeant First Class Terry O. P. Wallace upon his death in ground combat operations in Operation Iraqi Freedom. WHEREAS, Sergeant First Class Terry O. P. Wallace was a native of Winnsboro, Louisiana, and a graduate of Winnsboro High School, where he first met the person he would share his life with, his wife, Shunda; and WHEREAS, Sergeant First Class Wallace enlisted in the Army soon after graduating from high school, fulfilling his long held desire to serve his country as a member of its uniformed services; and WHEREAS, Sergeant First Class Wallace ultimately decided that he would remain in the Army and make serving his country his career; and WHEREAS, Sergeant First Class Wallace had been posted to a number of overseas stations during his fifteen-year military experience; and WHEREAS, Sergeant First Class Wallace was assigned to the 4th Battalion, 42nd Field Artillery, 1st Brigade, 4th Infantry Division based at Ft. Hood, Texas, when the unit received orders for and was deployed to Iraq; and WHEREAS, Sergeant First Class Wallace had served his country all over the world but this was his first tour in the Iraqi Theater of Operations; and WHEREAS, Sergeant First Class Wallace was proud to be a part of his nation's war on terrorism and serving actively in combat; and Page 1 of 2 SR NO.