DOCSLIB.ORG

The Gravitational Constant and the Planck's Units a Simplification Of

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Gravitational Constant and the Planck's Units a Simplification Of The Gravitational Constant and the Planck’s Units A Simplification of the Quantum Realm Espen Haug To cite this version: Espen Haug. The Gravitational Constant and the Planck’s Units A Simplification of the Quantum Realm. Physics Essays, Cenveo Publisher Services, 2016. hal-03234242 HAL Id: hal-03234242 https://hal.archives-ouvertes.fr/hal-03234242 Submitted on 25 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The Gravitational Constant and the Planck’s Units A Simplification of the Quantum Realm⇤ Espen Gaarder Haug† Norwegian University of Life Sciences (Dated: Preprint where final version published Physics Essays 2016) Abstract: In this paper, I suggest a new way to write the gravitational constant that makes all of the Planck units: Planck length, Planck time, Planck mass, and Planck energy more intuitive and simpler to understand. By writing the gravitational constant in a Planck functional form, we can rewrite all of the Planck units (without changing their values). Hopefully this can be a small step on the way to a better understanding of the quantum realm. R´esum´e: Dans cet article, je propose une nouvelle faon d’´ecrire la constante gravitationnelle qui rend toutes les unit´es de Planck, la longueur de Planck, le temps de Planck, la masse de Planck, et l’´energie de Planck, plus intuitives et plus simples comprendre. En crivant la constante gravitationnelle sous une forme fonctionnelle de Planck, nous pouvons r´e´ecrire toutes les unit´es de Planck (sans changer leur valeur). Nous esp´erons que cela puisse tre un petit pas vers une comprhension encore meilleure du domaine quantique. Key words: Gravitational constant, Max Planck, Planck units: length, time, mass, energy, quan- tum physics. I. A NEW PERSPECTIVE ON THE PLANCK UNITS Next the Planck mass in this context results in We suggest that Newton’s gravitational constant[1] can be written as a function of Planck’s reduced constant ~c ~c ~ 1 mp = = 2 3 = (4) G lpc l c 2 3 s p s p lpc ~ Gp = (1) ~ Based on the gravitational constant, the Planck energy where ~ is the reduced Planck’s constant [2], c is the can be simplified to well tested round-trip speed of light, and lp is the Planck length [3]. We could call this Planck’s form of the grav- itational constant. The Planck length lp is calibrated so 2 ~c 2 ~ 1 2 ~ Ep = mpc = c = c = c (5) that Gp matches our best estimate for the gravitational sGp lp c lp constant. We can use the gravitational constant to find the Planck length, or the Planck length to set the grav- And finally we can also rewrite the reduced Compton itational constant. In our view, the Planck form of the wavelength: gravitational constant enables us to rewrite Planck’s con- stants in a way that simplifies and gives deeper insight, potentially opening up the path for new interpretations ~ ~ 1 = 1 = 1 = lp (6) mpc ~ c in physics. lp c lp Based on this, the Planck length is given by I summarize a series of rewritten Planck units in Table 1. l2 c3 G p One interesting thing to note from the table is that in ~ p ~ ~ lp = = = lp (2) the Planck form of the Planck units, one has c1.5, c2.5, c3 s c3 r c3.5 and c4.5 as well as c4, c5, c7, c8 and it is very hard to Here the Planck length is simply our constant lp.Fur- find any intuition in c powered to such numbers. In the ther, the Planck time in this context is rewritten forms introduced in this paper, we only have c in most of the units, and c2 for only the Planck power and Planck intensity. We have gotten rid of the square 2 3 lpc root as well as the high-powered, non-intuitive notation ~Gp ~ lp t = = ~ = (3) in the Planck units. p 5 s 5 One could arguer thatc rewritingc the gravitationalc con- stant in this way creates a circular argument, since the 2 TABLE I. The table shows the standard Planck units and the units rewritten in the simpler and more intuitive form. Units: “Normal”-form: Simplified-form: 2 3 11 lpc Gravitational constant G 6.67408 10− Gp = ⇡ ⇥ ~ ~G Planck length lp = c3 lp = lp q ~G lp Planck time tp = c5 tp = c q ~c ~ 1 Planck mass mp = mp = G lp c q~c5 ~ Planck energy Ep = Ep = c G lp 2 ~ ~ 1 2 Relationship mass and energy Ep = qmpc c = c lp lp c ~ Reduced Compton wavelength lp mpc 2 ~G 2 2 Planck area lp = c3 lp = lp 3 ~3G3 3 3 Planck volume lp = c9 lp = lp 4 Ep ~ c ~ c Planck force Fp = =q = Fp = lp lptp G lp lp 5 2 Ep c ~ c Planck power Pp = = Pp = tp G lp lp 1 5 ~ mp c lp c ~ 1 ~ 1 Planck mass density ⇢p = 3 = 2 ⇢p = 3 = 4 = 3 lp ~G lp lp c lp clp 7 ~ c E Ep c E lp ~ ~ c Planck energy density ⇢p = 3 = 2 ⇢p = 3 = 4 c = 3 lp ~G lp lp lp lp 8 2 c ~ c Planck intensity Ip = ⇢pc = 2 Ip = 3 ~G lp lp 1 c5 1 c Planck frequency !p = = !p = = tp ~G lp lp c 7 Fp ~ q c ~ c Planck pressure pp = 2 = 3 = 2 pp = 3 lp lptp ~G lp lp Planck length is derived from Newton’s gravitational con- adds support to the view that the Planck length could be stant. We should consider this in a historical perspective. just as fundamental as big G, if not more so. Although Newton’s gravitational constant was discovered long be- our technology is not advanced enough yet for precision fore the Planck length was even considered (in 1906). in such analysis, it may be in the not too distant future. The Planck length was derived from the gravitational One could argue that the equation is biting its own constant, the speed of light, and the Planck constant. tail as the maximum velocity is a function of the Planck However, it could have taken place the other way around length, e.g. we have simply invented a circular solution if the Planck length had been introduced as a “hypothet- to the Planck length with no real solution. However, this ical” fundamental entity first. The fact that Newton’s is a misconception. The important point is that vmax gravitational constant was discovered before the Planck can be measured experimentally (At a minimum within length was established does not necessarily make it more a thought experiment, that is until our technology for fundamental than the Planck length. Newton’s gravita- accelerating particles get more advanced.) and we know tional constant was likely discovered first because it was that vmax is the composite structure, thus we can use this easier to measure; this is true even if Big G is hard to to extract lp. We typically know the reduced Compton measure accurately; see [4–8]. Even so, Big G is easier wavelength (of an electron, for example) and we know c to measure (indirectly) than the Planck length. per definition; based on this, we can extract lp. Remark- Recently Haug [9, 10] has given a new theoretical in- ably, we need no knowledge of G or ~ to find the find the sight strongly suggesting that fundamental particles in Planck length and even the Planck mass. Einstein’s relativistic mass equation actually have a max- The maximum velocity derived by Haug can also be 1 imum velocity just below that of the speed of light. This written as a function of G, c, ~ and me can be seen as an additional “boundary condition” that a↵ects the interpretation of Einstein’s relativistic mass Gm2 l2 energy formula without actually changing the formula it- v = c 1 e = c 1 p c 1 1.7517 10 45 max ¯2 − self. The maximum velocity can be estimated accurately r − ~c s − λe ⇡ − ⇥ and is far above the velocity currently attained at the p (7) LHC. Still, what is most interesting in this context is Since vmax here is a function of the universal constants that the Planck length can be found experimentally to G, ~, and c one could try to argue that this is evidence be only a function of the speed of light c and the reduced Compton wavelength of the mass in question; the Haug v2 formula for the Planck length is: l = λ¯ 1 max .This 1 Thanks to an anonymous referee for pointing this out. p − c2 q 3 that lp must be a function of G and ~ and c and not From the rewriting above, we see that that fine struc- that G is a function of lp. In other words, that G must ture constants appear in several places and cancel each be a universal constant and lp is just a derived constant. other out, basically illustrating the Planck relationship However, the beauty of equation 7 is that G and ~ cancel described in 1906. In other words, the Planck length out and that we are left with vmax as a function of c, lp (and thereby the gravitational constant) is not directly only and the reduced Compton wavelength of the particle dependent on electromagnetic constants and we do not in question, λ¯, and not of G and ~.
Load more

Recommended publications
  • Planck Mass Rotons As Cold Dark Matter and Quintessence* F
    Planck Mass Rotons as Cold Dark Matter and Quintessence* F. Winterberg Department of Physics, University of Nevada, Reno, USA Reprint requests to Prof. F. W.; Fax: (775) 784-1398 Z. Naturforsch. 57a, 202–204 (2002); received January 3, 2002 According to the Planck aether hypothesis, the vacuum of space is a superfluid made up of Planck mass particles, with the particles of the standard model explained as quasiparticle – excitations of this superfluid. Astrophysical data suggests that ≈70% of the vacuum energy, called quintessence, is a neg- ative pressure medium, with ≈26% cold dark matter and the remaining ≈4% baryonic matter and radi- ation. This division in parts is about the same as for rotons in superfluid helium, in terms of the Debye energy with a ≈70% energy gap and ≈25% kinetic energy. Having the structure of small vortices, the rotons act like a caviton fluid with a negative pressure. Replacing the Debye energy with the Planck en- ergy, it is conjectured that cold dark matter and quintessence are Planck mass rotons with an energy be- low the Planck energy. Key words: Analog Models of General Relativity. 1. Introduction The analogies between Yang Mills theories and vor- tex dynamics [3], and the analogies between general With greatly improved observational techniques a relativity and condensed matter physics [4 –10] sug- number of important facts about the physical content gest that string theory should perhaps be replaced by and large scale structure of our universe have emerged. some kind of vortex dynamics at the Planck scale. The They are: successful replacement of the bosonic string theory in 1.
    [Show full text]
  • Dark Energy and Dark Matter in a Superfluid Universe Abstract
    Dark Energy and Dark Matter in a Superfluid Universe1 Kerson Huang Massachusetts Institute of Technology, Cambridge, MA , USA 02139 and Institute of Advanced Studies, Nanyang Technological University, Singapore 639673 Abstract The vacuum is filled with complex scalar fields, such as the Higgs field. These fields serve as order parameters for superfluidity (quantum phase coherence over macroscopic distances), making the entire universe a superfluid. We review a mathematical model consisting of two aspects: (a) emergence of the superfluid during the big bang; (b) observable manifestations of superfluidity in the present universe. The creation aspect requires a self‐interacting scalar field that is asymptotically free, i.e., the interaction must grow from zero during the big bang, and this singles out the Halpern‐Huang potential, which has exponential behavior for large fields. It leads to an equivalent cosmological constant that decays like a power law, and this gives dark energy without "fine‐tuning". Quantum turbulence (chaotic vorticity) in the early universe was able to create all the matter in the universe, fulfilling the inflation scenario. In the present universe, the superfluid can be phenomenologically described by a nonlinear Klein‐Gordon equation. It predicts halos around galaxies with higher superfluid density, which is perceived as dark matter through gravitational lensing. In short, dark energy is the energy density of the cosmic superfluid, and dark matter arises from local fluctuations of the superfluid density 1 Invited talk at the Conference in Honor of 90th Birthday of Freeman Dyson, Institute of Advanced Studies, Nanyang Technological University, Singapore, 26‐29 August, 2013. 1 1. Overview Physics in the twentieth century was dominated by the theory of general relativity on the one hand, and quantum theory on the other.
    [Show full text]
  • An Atomic Physics Perspective on the New Kilogram Defined by Planck's Constant
    An atomic physics perspective on the new kilogram defined by Planck’s constant (Wolfgang Ketterle and Alan O. Jamison, MIT) (Manuscript submitted to Physics Today) On May 20, the kilogram will no longer be defined by the artefact in Paris, but through the definition1 of Planck’s constant h=6.626 070 15*10-34 kg m2/s. This is the result of advances in metrology: The best two measurements of h, the Watt balance and the silicon spheres, have now reached an accuracy similar to the mass drift of the ur-kilogram in Paris over 130 years. At this point, the General Conference on Weights and Measures decided to use the precisely measured numerical value of h as the definition of h, which then defines the unit of the kilogram. But how can we now explain in simple terms what exactly one kilogram is? How do fixed numerical values of h, the speed of light c and the Cs hyperfine frequency νCs define the kilogram? In this article we give a simple conceptual picture of the new kilogram and relate it to the practical realizations of the kilogram. A similar change occurred in 1983 for the definition of the meter when the speed of light was defined to be 299 792 458 m/s. Since the second was the time required for 9 192 631 770 oscillations of hyperfine radiation from a cesium atom, defining the speed of light defined the meter as the distance travelled by light in 1/9192631770 of a second, or equivalently, as 9192631770/299792458 times the wavelength of the cesium hyperfine radiation.
    [Show full text]
  • Quantum Vacuum Energy Density and Unifying Perspectives Between Gravity and Quantum Behaviour of Matter
    Annales de la Fondation Louis de Broglie, Volume 42, numéro 2, 2017 251 Quantum vacuum energy density and unifying perspectives between gravity and quantum behaviour of matter Davide Fiscalettia, Amrit Sorlib aSpaceLife Institute, S. Lorenzo in Campo (PU), Italy corresponding author, email: [email protected] bSpaceLife Institute, S. Lorenzo in Campo (PU), Italy Foundations of Physics Institute, Idrija, Slovenia email: [email protected] ABSTRACT. A model of a three-dimensional quantum vacuum based on Planck energy density as a universal property of a granular space is suggested. This model introduces the possibility to interpret gravity and the quantum behaviour of matter as two different aspects of the same origin. The change of the quantum vacuum energy density can be considered as the fundamental medium which determines a bridge between gravity and the quantum behaviour, leading to new interest- ing perspectives about the problem of unifying gravity with quantum theory. PACS numbers: 04. ; 04.20-q ; 04.50.Kd ; 04.60.-m. Key words: general relativity, three-dimensional space, quantum vac- uum energy density, quantum mechanics, generalized Klein-Gordon equation for the quantum vacuum energy density, generalized Dirac equation for the quantum vacuum energy density. 1 Introduction The standard interpretation of phenomena in gravitational fields is in terms of a fundamentally curved space-time. However, this approach leads to well known problems if one aims to find a unifying picture which takes into account some basic aspects of the quantum theory. For this reason, several authors advocated different ways in order to treat gravitational interaction, in which the space-time manifold can be considered as an emergence of the deepest processes situated at the fundamental level of quantum gravity.
    [Show full text]
  • Dimensional Analysis and the Theory of Natural Units
    LIBRARY TECHNICAL REPORT SECTION SCHOOL NAVAL POSTGRADUATE MONTEREY, CALIFORNIA 93940 NPS-57Gn71101A NAVAL POSTGRADUATE SCHOOL Monterey, California DIMENSIONAL ANALYSIS AND THE THEORY OF NATURAL UNITS "by T. H. Gawain, D.Sc. October 1971 lllp FEDDOCS public This document has been approved for D 208.14/2:NPS-57GN71101A unlimited release and sale; i^ distribution is NAVAL POSTGRADUATE SCHOOL Monterey, California Rear Admiral A. S. Goodfellow, Jr., USN M. U. Clauser Superintendent Provost ABSTRACT: This monograph has been prepared as a text on dimensional analysis for students of Aeronautics at this School. It develops the subject from a viewpoint which is inadequately treated in most standard texts hut which the author's experience has shown to be valuable to students and professionals alike. The analysis treats two types of consistent units, namely, fixed units and natural units. Fixed units include those encountered in the various familiar English and metric systems. Natural units are not fixed in magnitude once and for all but depend on certain physical reference parameters which change with the problem under consideration. Detailed rules are given for the orderly choice of such dimensional reference parameters and for their use in various applications. It is shown that when transformed into natural units, all physical quantities are reduced to dimensionless form. The dimension- less parameters of the well known Pi Theorem are shown to be in this category. An important corollary is proved, namely that any valid physical equation remains valid if all dimensional quantities in the equation be replaced by their dimensionless counterparts in any consistent system of natural units.
    [Show full text]
  • Chapter 5 Dimensional Analysis and Similarity
    Chapter 5 Dimensional Analysis and Similarity Motivation. In this chapter we discuss the planning, presentation, and interpretation of experimental data. We shall try to convince you that such data are best presented in dimensionless form. Experiments which might result in tables of output, or even mul- tiple volumes of tables, might be reduced to a single set of curves—or even a single curve—when suitably nondimensionalized. The technique for doing this is dimensional analysis. Chapter 3 presented gross control-volume balances of mass, momentum, and en- ergy which led to estimates of global parameters: mass flow, force, torque, total heat transfer. Chapter 4 presented infinitesimal balances which led to the basic partial dif- ferential equations of fluid flow and some particular solutions. These two chapters cov- ered analytical techniques, which are limited to fairly simple geometries and well- defined boundary conditions. Probably one-third of fluid-flow problems can be attacked in this analytical or theoretical manner. The other two-thirds of all fluid problems are too complex, both geometrically and physically, to be solved analytically. They must be tested by experiment. Their behav- ior is reported as experimental data. Such data are much more useful if they are ex- pressed in compact, economic form. Graphs are especially useful, since tabulated data cannot be absorbed, nor can the trends and rates of change be observed, by most en- gineering eyes. These are the motivations for dimensional analysis. The technique is traditional in fluid mechanics and is useful in all engineering and physical sciences, with notable uses also seen in the biological and social sciences.
    [Show full text]
  • Units and Magnitudes (Lecture Notes)
    physics 8.701 topic 2 Frank Wilczek Units and Magnitudes (lecture notes) This lecture has two parts. The first part is mainly a practical guide to the measurement units that dominate the particle physics literature, and culture. The second part is a quasi-philosophical discussion of deep issues around unit systems, including a comparison of atomic, particle ("strong") and Planck units. For a more extended, profound treatment of the second part issues, see arxiv.org/pdf/0708.4361v1.pdf . Because special relativity and quantum mechanics permeate modern particle physics, it is useful to employ units so that c = ħ = 1. In other words, we report velocities as multiples the speed of light c, and actions (or equivalently angular momenta) as multiples of the rationalized Planck's constant ħ, which is the original Planck constant h divided by 2π. 27 August 2013 physics 8.701 topic 2 Frank Wilczek In classical physics one usually keeps separate units for mass, length and time. I invite you to think about why! (I'll give you my take on it later.) To bring out the "dimensional" features of particle physics units without excess baggage, it is helpful to keep track of powers of mass M, length L, and time T without regard to magnitudes, in the form When these are both set equal to 1, the M, L, T system collapses to just one independent dimension. So we can - and usually do - consider everything as having the units of some power of mass. Thus for energy we have while for momentum 27 August 2013 physics 8.701 topic 2 Frank Wilczek and for length so that energy and momentum have the units of mass, while length has the units of inverse mass.
    [Show full text]
  • Estimation of Forest Aboveground Biomass and Uncertainties By
    Urbazaev et al. Carbon Balance Manage (2018) 13:5 https://doi.org/10.1186/s13021-018-0093-5 RESEARCH Open Access Estimation of forest aboveground biomass and uncertainties by integration of feld measurements, airborne LiDAR, and SAR and optical satellite data in Mexico Mikhail Urbazaev1,2* , Christian Thiel1, Felix Cremer1, Ralph Dubayah3, Mirco Migliavacca4, Markus Reichstein4 and Christiane Schmullius1 Abstract Background: Information on the spatial distribution of aboveground biomass (AGB) over large areas is needed for understanding and managing processes involved in the carbon cycle and supporting international policies for climate change mitigation and adaption. Furthermore, these products provide important baseline data for the development of sustainable management strategies to local stakeholders. The use of remote sensing data can provide spatially explicit information of AGB from local to global scales. In this study, we mapped national Mexican forest AGB using satellite remote sensing data and a machine learning approach. We modelled AGB using two scenarios: (1) extensive national forest inventory (NFI), and (2) airborne Light Detection and Ranging (LiDAR) as reference data. Finally, we propagated uncertainties from feld measurements to LiDAR-derived AGB and to the national wall-to-wall forest AGB map. Results: The estimated AGB maps (NFI- and LiDAR-calibrated) showed similar goodness-of-ft statistics (R­ 2, Root Mean Square Error (RMSE)) at three diferent scales compared to the independent validation data set. We observed diferent spatial patterns of AGB in tropical dense forests, where no or limited number of NFI data were available, with higher AGB values in the LiDAR-calibrated map. We estimated much higher uncertainties in the AGB maps based on two-stage up-scaling method (i.e., from feld measurements to LiDAR and from LiDAR-based estimates to satel- lite imagery) compared to the traditional feld to satellite up-scaling.
    [Show full text]
  • Section 22-3: Energy, Momentum and Radiation Pressure
    Answer to Essential Question 22.2: (a) To find the wavelength, we can combine the equation with the fact that the speed of light in air is 3.00 " 108 m/s. Thus, a frequency of 1 " 1018 Hz corresponds to a wavelength of 3 " 10-10 m, while a frequency of 90.9 MHz corresponds to a wavelength of 3.30 m. (b) Using Equation 22.2, with c = 3.00 " 108 m/s, gives an amplitude of . 22-3 Energy, Momentum and Radiation Pressure All waves carry energy, and electromagnetic waves are no exception. We often characterize the energy carried by a wave in terms of its intensity, which is the power per unit area. At a particular point in space that the wave is moving past, the intensity varies as the electric and magnetic fields at the point oscillate. It is generally most useful to focus on the average intensity, which is given by: . (Eq. 22.3: The average intensity in an EM wave) Note that Equations 22.2 and 22.3 can be combined, so the average intensity can be calculated using only the amplitude of the electric field or only the amplitude of the magnetic field. Momentum and radiation pressure As we will discuss later in the book, there is no mass associated with light, or with any EM wave. Despite this, an electromagnetic wave carries momentum. The momentum of an EM wave is the energy carried by the wave divided by the speed of light. If an EM wave is absorbed by an object, or it reflects from an object, the wave will transfer momentum to the object.
    [Show full text]
  • Three-Dimensional Analysis of the Hot-Spot Fuel Temperature in Pebble Bed and Prismatic Modular Reactors
    Transactions of the Korean Nuclear Society Spring Meeting Chuncheon, Korea, May 25-26 2006 Three-Dimensional Analysis of the Hot-Spot Fuel Temperature in Pebble Bed and Prismatic Modular Reactors W. K. In,a S. W. Lee,a H. S. Lim,a W. J. Lee a a Korea Atomic Energy Research Institute, P. O. Box 105, Yuseong, Daejeon, Korea, 305-600, [email protected] 1. Introduction thousands of fuel particles. The pebble diameter is 60mm High temperature gas-cooled reactors(HTGR) have with a 5mm unfueled layer. Unstaggered and 2-D been reviewed as potential sources for future energy needs, staggered arrays of 3x3 pebbles as shown in Fig. 1 are particularly for a hydrogen production. Among the simulated to predict the temperature distribution in a hot- HTGRs, the pebble bed reactor(PBR) and a prismatic spot pebble core. Total number of nodes is 1,220,000 and modular reactor(PMR) are considered as the nuclear heat 1,060,000 for the unstaggered and staggered models, source in Korea’s nuclear hydrogen development and respectively. demonstration project. PBR uses coated fuel particles The GT-MHR(PMR) reactor core is loaded with an embedded in spherical graphite fuel pebbles. The fuel annular stack of hexahedral prismatic fuel assemblies, pebbles flow down through the core during an operation. which form 102 columns consisting of 10 fuel blocks PMR uses graphite fuel blocks which contain cylindrical stacked axially in each column. Each fuel block is a fuel compacts consisting of the fuel particles. The fuel triangular array of a fuel compact channel, a coolant blocks also contain coolant passages and locations for channel and a channel for a control rod.
    [Show full text]
  • Improving the Accuracy of the Numerical Values of the Estimates Some Fundamental Physical Constants
    Improving the accuracy of the numerical values of the estimates some fundamental physical constants. Valery Timkov, Serg Timkov, Vladimir Zhukov, Konstantin Afanasiev To cite this version: Valery Timkov, Serg Timkov, Vladimir Zhukov, Konstantin Afanasiev. Improving the accuracy of the numerical values of the estimates some fundamental physical constants.. Digital Technologies, Odessa National Academy of Telecommunications, 2019, 25, pp.23 - 39. hal-02117148 HAL Id: hal-02117148 https://hal.archives-ouvertes.fr/hal-02117148 Submitted on 2 May 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Improving the accuracy of the numerical values of the estimates some fundamental physical constants. Valery F. Timkov1*, Serg V. Timkov2, Vladimir A. Zhukov2, Konstantin E. Afanasiev2 1Institute of Telecommunications and Global Geoinformation Space of the National Academy of Sciences of Ukraine, Senior Researcher, Ukraine. 2Research and Production Enterprise «TZHK», Researcher, Ukraine. *Email: [email protected] The list of designations in the text: l
    [Show full text]
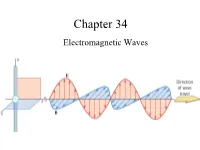
  • Properties of Electromagnetic Waves Any Electromagnetic Wave Must Satisfy Four Basic Conditions: 1
    Chapter 34 Electromagnetic Waves The Goal of the Entire Course Maxwell’s Equations: Maxwell’s Equations James Clerk Maxwell •1831 – 1879 •Scottish theoretical physicist •Developed the electromagnetic theory of light •His successful interpretation of the electromagnetic field resulted in the field equations that bear his name. •Also developed and explained – Kinetic theory of gases – Nature of Saturn’s rings – Color vision Start at 12:50 https://www.learner.org/vod/vod_window.html?pid=604 Correcting Ampere’s Law Two surfaces S1 and S2 near the plate of a capacitor are bounded by the same path P. Ampere’s Law states that But it is zero on S2 since there is no conduction current through it. This is a contradiction. Maxwell fixed it by introducing the displacement current: Fig. 34-1, p. 984 Maxwell hypothesized that a changing electric field creates an induced magnetic field. Induced Fields . An increasing solenoid current causes an increasing magnetic field, which induces a circular electric field. An increasing capacitor charge causes an increasing electric field, which induces a circular magnetic field. Slide 34-50 Displacement Current d d(EA)d(q / ε) 1 dq E 0 dt dt dt ε0 dt dq d ε E dt0 dt The displacement current is equal to the conduction current!!! Bsd μ I μ ε I o o o d Maxwell’s Equations The First Unified Field Theory In his unified theory of electromagnetism, Maxwell showed that electromagnetic waves are a natural consequence of the fundamental laws expressed in these four equations: q EABAdd 0 εo dd Edd s BE B s μ I μ ε dto o o dt QuickCheck 34.4 The electric field is increasing.
    [Show full text]