DOCSLIB.ORG

Binary Search Trees

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Binary Search Trees Binary Search Trees 15-121 Fall 2020 Margaret Reid-Miller Today • Prune leaves example • Binary Search Trees • Definition • Algorithms for • Contains • Add • Remove • Complexity Fall 2020 15-121 (Reid-Miller) 2 Remove all leaves from tree t public static <E> void prune(BTNode<E> t){ if (t == null) return; BTNode<E> left = t.getLeft(); if (left != null) { if (isLeaf(left)) t.setLeft(null); else prune(left); } BTNode<E> right = t.getRight(); if (right != null) { if (isLeaf(right)) t.setRight(null); else prune(right); } } Fall 2020 15-121 (Reid-Miller) 3 Remove all leaves from tree t Return reference to the resulting tree public static <E> BTNode<E> prune(BTNode<E> t){ What are the base case(s)? What does the recursive cases return? How do you update the tree? Submit answers to https://forms.gle/a5qj8rTF1tndp1tH6 Fall 2020 15-121 (Reid-Miller) 4 Remove all leaves from tree t Return reference to the resulting tree public static <E> BTNode<E> prune(BTNode<E> t){ if (t == null || isLeaf(t)) return null; t.setLeft = prune(t.getLeft()); t.setRight = prune(t.getRight()); return t; } Fall 2020 15-121 (Reid-Miller) 5 More Terminology • A perfect binary tree is a binary tree such that - all leaves have the same level, and - every non-leaf node has 2 children. • A full tree is a binary tree such that - every non-leaf node has 2 children. • A complete binary tree is a binary tree such that - every level of the tree has the maximum number of nodes - except possibly at the deepest level, where the nodes are as far left as possible. Fall 2020 15-121 (Reid-Miller) 6 Examples A A B C B C D E F G D E F PERFECT COMPLETE (COMPLETE (but not PERFECT and FULL) and not FULL) Fall 2020 15-121 (Reid-Miller) 7 Binary Search Trees Fall 2020 15-121 (Reid-Miller) 8 Binary Search Trees • A binary tree T is a binary search tree if • T is empty, or • T has two subtrees, TL and TR, such that • All the values in TL are less than the value in the root of T, • All the values in TR are greater than the value in the root of T, and • TL and TR are binary search trees • Typically, duplicates are not allowed. Fall 2020 15-121 (Reid-Miller) 9 Example: Is this a BST? 4 4 1 7 1 7 6 8 3 6 8 3 9 9 no yes Fall 2020 15-121 (Reid-Miller) 10 Elements of a BinarySearchTree must be Comparable public class BinarySearchTree <E extends Comparable<E>> { private class BTNode { // inner class private E data private BTNode left; private BTNode right; private BTNode(E data) { this.data = data} } private BTNode root; // field public BinarySearchTree() { // constructor root = null; Fall 2020} 15-121 (Reid-Miller) 11 Example : max How did we find the maximum value in a Binary Tree? Recursively got the max of the root and the left and right subtrees. If the tree is a Binary Search Tree (BST), do we need to search the whole tree? No Where is the maximum in a Binary Search Tree? The right most node Fall 2020 15-121 (Reid-Miller) 12 Where is the maximum? 62 15 11 96 40 39 83 26 45 21 52 Fall 2020 15-121 (Reid-Miller) 13 The node with the maximum value in a BST is the rightmost node. // recursive implementation public E max() { if (root == null) return null; return max(root); } //precondition: tree is not empty private E max(BTNode t) { if (_______________)t.right == null return t.data; else return max(t.right); } Only one recursive call! Fall 2020 15-121 (Reid-Miller) 14 Searching for 83 and 42 62 62 11 96 11 96 39 83 39 83 21 45 21 45 NOT FOUND Fall 2020 15-121 (Reid-Miller) 15 To find an element follow a path in the BST // iterative implementation public boolean contains(E obj) { BTNode t = root; while (t != null) { if (obj.equals(t.data)) return true; else if (obj.compareTo(t.data) < 0) t = t.left; else t = t.right; } return false; } Fall 2020 15-121 (Reid-Miller) 17 Adding to a BST • Where should we add an element to a BST? • If the tree is empty, make the element the root • Otherwise attach it as a leaf node. Fall 2020 15-121 (Reid-Miller) 18 Add to a BST in the order given 62 62 96 11 39 21 83 45 11 96 39 83 21 45 Fall 2020 15-121 (Reid-Miller) 19 Add element as a leaf node // recursive implementation public void add(E obj) { root = add(root, obj); } // returns a reference to a tree with obj in it private BTNode add(BTNode t, E obj) { if (t == null) return new BTNode(obj); else if (obj.compareTo(t.data) < 0) t.left = add(t.left, obj); else if (obj.compareTo(t.data) > 0) t.right = add(t.right, obj); // else already in the tree return t; } Fall 2020 15-121 (Reid-Miller) 20 Exercise: add • Draw the binary search tree that results from adding the each character to an empty tree in the following order: C A R N E G I E M E L L O N Do not add any duplicate values to your tree. Fall 2020 15-121 (Reid-Miller) 24 C A R N E G I E M E L L O N Fall 2020 15-121 (Reid-Miller) 25 Runtime of add on a perfect BST • A perfect binary search tree with height H has how many nodes? • n = 1 + 2 + 4 + ... + 2H = 2H+1 - 1 • Thus, H = log2(n+1) - 1. • Add will take O(log n) time on a perfect BST • We have to examine one node at each level before we find the insertion point, and height is H. Fall 2020 15-121 (Reid-Miller) 26 Worst-case runtime of add on a BST • Are all BSTs perfect? NO! Add the following numbers in order into a BST: 11 21 39 45 62 83 96 What do you get? • An add will take O(n) time in the worst case on an arbitrary BST since there may be up to n levels in a BST with n nodes. Fall 2020 15-121 (Reid-Miller) 27 Aside: How many BSTs with n distinct values have height n? 1 5 1 2 4 5 3 3 2 4 2 4 3 5 1 Total number BST with height n is 2n-1 That's a small fraction of the total number BST: O(4n) Fall 2020 15-121 (Reid-Miller) 28 Removing from a BST General idea: • Search for the item to remove until either: - the item is found (at the root of a subtree) or - we reach a leaf and the item is not found • If the item is found: • remove the root (of the subtree) and • replace it with its closest value (either its in-order predecessor or successor) Fall 2020 15-121 (Reid-Miller) 31 A Predecessor is largest value in left subtree K Successor is smallest value in right subtree D R C E O W H M S L N T Suppose we replace the root with its in-order predecessor. Where is the in-order predecessor? • on the left side and • is the rightmost node (max on left side) Three cases: 1. no predecessor 2. predecessor is left child 3. predecessor is rightmost of left child Fall 2020 15-121 (Reid-Miller) 34 Case 1: The root has no predecessor • Return the right subtree (to the parent of the root) r S S Fall 2020 15-121 (Reid-Miller) 35 Removing from a BST Data value is found at a root with no left child • Return the right subtree • Result is to set the parent reference to its grandchild. • Example: Remove 31. 64 null X root: null 31 49 Fall 2020 15-121 (Reid-Miller) 37 Case 2: The predecessor is the left child of the root • Copy the data from the root's left child into the root. • Set the root's left reference to the left child of the root's left child. root r root p p S A S A Subtree A could be null Fall 2020 15-121 (Reid-Miller) 38 Removing from a BST Predecessor is left child • Example: 45 Remove 29. root 29 X 17 predecessor of 29 17 null 36 6 Fall 2020 15-121 (Reid-Miller) 39 Case 3: The root’s predecessor is rightmost of the left child • Copy the data from the predecessor to the root • Then set the predecessor's parent to reference its left child. root r root p A S A S p G G Subtree G could be null Fall 2020 15-121 (Reid-Miller) 40 Removing from a BST Predecessor is right of left child 45 • Example: root 29 Remove 29. 27 15 36 6 21 X 27 null predecessor of 29 24 Fall 2020 15-121 (Reid-Miller) 41 Complexity of Binary Search Trees Worst case Best case contains O(height) O(1) add O(height) O(1) remove O(height) O(1) traverse O(n) Worst-case height of binary search tree: O(n) Best-case height of binary search tree: O(log n) Balanced Binary Search Trees have height O(log n): E.g, AVL, Red-Black, Splay, Treaps, Weight-balanced, …Fall 2020 15-121 (Reid-Miller) 42.
Load more

Recommended publications
  • 1 Suffix Trees
    This material takes about 1.5 hours. 1 Suffix Trees Gusfield: Algorithms on Strings, Trees, and Sequences. Weiner 73 “Linear Pattern-matching algorithms” IEEE conference on automata and switching theory McCreight 76 “A space-economical suffix tree construction algorithm” JACM 23(2) 1976 Chen and Seifras 85 “Efficient and Elegegant Suffix tree construction” in Apos- tolico/Galil Combninatorial Algorithms on Words Another “search” structure, dedicated to strings. Basic problem: match a “pattern” (of length m) to “text” (of length n) • goal: decide if a given string (“pattern”) is a substring of the text • possibly created by concatenating short ones, eg newspaper • application in IR, also computational bio (DNA seqs) • if pattern avilable first, can build DFA, run in time linear in text • if text available first, can build suffix tree, run in time linear in pattern. • applications in computational bio. First idea: binary tree on strings. Inefficient because run over pattern many times. • fractional cascading? • realize only need one character at each node! Tries: • used to store dictionary of strings • trees with children indexed by “alphabet” • time to search equal length of query string • insertion ditto. • optimal, since even hashing requires this time to hash. • but better, because no “hash function” computed. • space an issue: – using array increases stroage cost by |Σ| – using binary tree on alphabet increases search time by log |Σ| 1 – ok for “const alphabet” – if really fussy, could use hash-table at each node. • size in worst case: sum of word lengths (so pretty much solves “dictionary” problem. But what about substrings? • Relevance to DNA searches • idea: trie of all n2 substrings • equivalent to trie of all n suffixes.
    [Show full text]
  • Tree-Combined Trie: a Compressed Data Structure for Fast IP Address Lookup
    (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 6, No. 12, 2015 Tree-Combined Trie: A Compressed Data Structure for Fast IP Address Lookup Muhammad Tahir Shakil Ahmed Department of Computer Engineering, Department of Computer Engineering, Sir Syed University of Engineering and Technology, Sir Syed University of Engineering and Technology, Karachi Karachi Abstract—For meeting the requirements of the high-speed impact their forwarding capacity. In order to resolve two main Internet and satisfying the Internet users, building fast routers issues there are two possible solutions one is IPv6 IP with high-speed IP address lookup engine is inevitable. addressing scheme and second is Classless Inter-domain Regarding the unpredictable variations occurred in the Routing or CIDR. forwarding information during the time and space, the IP lookup algorithm should be able to customize itself with temporal and Finding a high-speed, memory-efficient and scalable IP spatial conditions. This paper proposes a new dynamic data address lookup method has been a great challenge especially structure for fast IP address lookup. This novel data structure is in the last decade (i.e. after introducing Classless Inter- a dynamic mixture of trees and tries which is called Tree- Domain Routing, CIDR, in 1994). In this paper, we will Combined Trie or simply TC-Trie. Binary sorted trees are more discuss only CIDR. In addition to these desirable features, advantageous than tries for representing a sparse population reconfigurability is also of great importance; true because while multibit tries have better performance than trees when a different points of this huge heterogeneous structure of population is dense.
    [Show full text]
  • Balanced Trees Part One
    Balanced Trees Part One Balanced Trees ● Balanced search trees are among the most useful and versatile data structures. ● Many programming languages ship with a balanced tree library. ● C++: std::map / std::set ● Java: TreeMap / TreeSet ● Many advanced data structures are layered on top of balanced trees. ● We’ll see several later in the quarter! Where We're Going ● B-Trees (Today) ● A simple type of balanced tree developed for block storage. ● Red/Black Trees (Today/Thursday) ● The canonical balanced binary search tree. ● Augmented Search Trees (Thursday) ● Adding extra information to balanced trees to supercharge the data structure. Outline for Today ● BST Review ● Refresher on basic BST concepts and runtimes. ● Overview of Red/Black Trees ● What we're building toward. ● B-Trees and 2-3-4 Trees ● Simple balanced trees, in depth. ● Intuiting Red/Black Trees ● A much better feel for red/black trees. A Quick BST Review Binary Search Trees ● A binary search tree is a binary tree with 9 the following properties: 5 13 ● Each node in the BST stores a key, and 1 6 10 14 optionally, some auxiliary information. 3 7 11 15 ● The key of every node in a BST is strictly greater than all keys 2 4 8 12 to its left and strictly smaller than all keys to its right. Binary Search Trees ● The height of a binary search tree is the 9 length of the longest path from the root to a 5 13 leaf, measured in the number of edges. 1 6 10 14 ● A tree with one node has height 0.
    [Show full text]
  • CSE 326: Data Structures Binary Search Trees
    Announcements (1/23/09) CSE 326: Data Structures • HW #2 due now • HW #3 out today, due at beginning of class next Binary Search Trees Friday. • Project 2A due next Wed. night. Steve Seitz Winter 2009 • Read Chapter 4 1 2 ADTs Seen So Far The Dictionary ADT • seitz •Data: Steve • Stack •Priority Queue Seitz –a set of insert(seitz, ….) CSE 592 –Push –Insert (key, value) pairs –Pop – DeleteMin •ericm6 Eric • Operations: McCambridge – Insert (key, value) CSE 218 •Queue find(ericm6) – Find (key) • ericm6 • soyoung – Enqueue Then there is decreaseKey… Eric, McCambridge,… – Remove (key) Soyoung Shin – Dequeue CSE 002 •… The Dictionary ADT is also 3 called the “Map ADT” 4 A Modest Few Uses Implementations insert find delete •Sets • Unsorted Linked-list • Dictionaries • Networks : Router tables • Operating systems : Page tables • Unsorted array • Compilers : Symbol tables • Sorted array Probably the most widely used ADT! 5 6 Binary Trees Binary Tree: Representation • Binary tree is A – a root left right – left subtree (maybe empty) A pointerpointer A – right subtree (maybe empty) B C B C B C • Representation: left right left right pointerpointer pointerpointer D E F D E F Data left right G H D E F pointer pointer left right left right left right pointerpointer pointerpointer pointerpointer I J 7 8 Tree Traversals Inorder Traversal void traverse(BNode t){ A traversal is an order for if (t != NULL) visiting all the nodes of a tree + traverse (t.left); process t.element; Three types: * 5 traverse (t.right); • Pre-order: Root, left subtree, right subtree 2 4 } • In-order: Left subtree, root, right subtree } (an expression tree) • Post-order: Left subtree, right subtree, root 9 10 Binary Tree: Special Cases Binary Tree: Some Numbers… Recall: height of a tree = longest path from root to leaf.
    [Show full text]
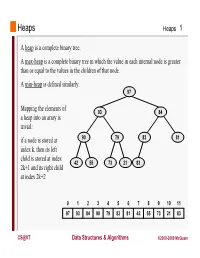
  • Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
    Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { .
    [Show full text]
  • Assignment 3: Kdtree ______Due June 4, 11:59 PM
    CS106L Handout #04 Spring 2014 May 15, 2014 Assignment 3: KDTree _________________________________________________________________________________________________________ Due June 4, 11:59 PM Over the past seven weeks, we've explored a wide array of STL container classes. You've seen the linear vector and deque, along with the associative map and set. One property common to all these containers is that they are exact. An element is either in a set or it isn't. A value either ap- pears at a particular position in a vector or it does not. For most applications, this is exactly what we want. However, in some cases we may be interested not in the question “is X in this container,” but rather “what value in the container is X most similar to?” Queries of this sort often arise in data mining, machine learning, and computational geometry. In this assignment, you will implement a special data structure called a kd-tree (short for “k-dimensional tree”) that efficiently supports this operation. At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimen- sional space. That is, you could use a kd-tree to store a collection of points in the Cartesian plane, in three-dimensional space, etc. You could also use a kd-tree to store biometric data, for example, by representing the data as an ordered tuple, perhaps (height, weight, blood pressure, cholesterol). However, a kd-tree cannot be used to store collections of other data types, such as strings. Also note that while it's possible to build a kd-tree to hold data of any dimension, all of the data stored in a kd-tree must have the same dimension.
    [Show full text]
  • CSCI 333 Data Structures Binary Trees Binary Tree Example Full And
    Notes with the dark blue background CSCI 333 were prepared by the textbook author Data Structures Clifford A. Shaffer Chapter 5 Department of Computer Science 18, 20, 23, and 25 September 2002 Virginia Tech Copyright © 2000, 2001 Binary Trees Binary Tree Example A binary tree is made up of a finite set of Notation: Node, nodes that is either empty or consists of a children, edge, node called the root together with two parent, ancestor, binary trees, called the left and right descendant, path, subtrees, which are disjoint from each depth, height, level, other and from the root. leaf node, internal node, subtree. Full and Complete Binary Trees Full Binary Tree Theorem (1) Full binary tree: Each node is either a leaf or Theorem: The number of leaves in a non-empty internal node with exactly two non-empty children. full binary tree is one more than the number of internal nodes. Complete binary tree: If the height of the tree is d, then all leaves except possibly level d are Proof (by Mathematical Induction): completely full. The bottom level has all nodes to the left side. Base case: A full binary tree with 1 internal node must have two leaf nodes. Induction Hypothesis: Assume any full binary tree T containing n-1 internal nodes has n leaves. 1 Full Binary Tree Theorem (2) Full Binary Tree Corollary Induction Step: Given tree T with n internal Theorem: The number of null pointers in a nodes, pick internal node I with two leaf children. non-empty tree is one more than the Remove I’s children, call resulting tree T’.
    [Show full text]
  • Tree Structures
    Tree Structures Definitions: o A tree is a connected acyclic graph. o A disconnected acyclic graph is called a forest o A tree is a connected digraph with these properties: . There is exactly one node (Root) with in-degree=0 . All other nodes have in-degree=1 . A leaf is a node with out-degree=0 . There is exactly one path from the root to any leaf o The degree of a tree is the maximum out-degree of the nodes in the tree. o If (X,Y) is a path: X is an ancestor of Y, and Y is a descendant of X. Root X Y CSci 1112 – Algorithms and Data Structures, A. Bellaachia Page 1 Level of a node: Level 0 or 1 1 or 2 2 or 3 3 or 4 Height or depth: o The depth of a node is the number of edges from the root to the node. o The root node has depth zero o The height of a node is the number of edges from the node to the deepest leaf. o The height of a tree is a height of the root. o The height of the root is the height of the tree o Leaf nodes have height zero o A tree with only a single node (hence both a root and leaf) has depth and height zero. o An empty tree (tree with no nodes) has depth and height −1. o It is the maximum level of any node in the tree. CSci 1112 – Algorithms and Data Structures, A.
    [Show full text]
  • Binary Search Tree
    ADT Binary Search Tree! Ellen Walker! CPSC 201 Data Structures! Hiram College! Binary Search Tree! •" Value-based storage of information! –" Data is stored in order! –" Data can be retrieved by value efficiently! •" Is a binary tree! –" Everything in left subtree is < root! –" Everything in right subtree is >root! –" Both left and right subtrees are also BST#s! Operations on BST! •" Some can be inherited from binary tree! –" Constructor (for empty tree)! –" Inorder, Preorder, and Postorder traversal! •" Some must be defined ! –" Insert item! –" Delete item! –" Retrieve item! The Node<E> Class! •" Just as for a linked list, a node consists of a data part and links to successor nodes! •" The data part is a reference to type E! •" A binary tree node must have links to both its left and right subtrees! The BinaryTree<E> Class! The BinaryTree<E> Class (continued)! Overview of a Binary Search Tree! •" Binary search tree definition! –" A set of nodes T is a binary search tree if either of the following is true! •" T is empty! •" Its root has two subtrees such that each is a binary search tree and the value in the root is greater than all values of the left subtree but less than all values in the right subtree! Overview of a Binary Search Tree (continued)! Searching a Binary Tree! Class TreeSet and Interface Search Tree! BinarySearchTree Class! BST Algorithms! •" Search! •" Insert! •" Delete! •" Print values in order! –" We already know this, it#s inorder traversal! –" That#s why it#s called “in order”! Searching the Binary Tree! •" If the tree is
    [Show full text]
  • 6.172 Lecture 19 : Cache-Oblivious B-Tree (Tokudb)
    How TokuDB Fractal TreeTM Indexes Work Bradley C. Kuszmaul Guest Lecture in MIT 6.172 Performance Engineering, 18 November 2010. 6.172 —How Fractal Trees Work 1 My Background • I’m an MIT alum: MIT Degrees = 2 × S.B + S.M. + Ph.D. • I was a principal architect of the Connection Machine CM-5 super­ computer at Thinking Machines. • I was Assistant Professor at Yale. • I was Akamai working on network mapping and billing. • I am research faculty in the SuperTech group, working with Charles. 6.172 —How Fractal Trees Work 2 Tokutek A few years ago I started collaborating with Michael Bender and Martin Farach-Colton on how to store data on disk to achieve high performance. We started Tokutek to commercialize the research. 6.172 —How Fractal Trees Work 3 I/O is a Big Bottleneck Sensor Query Systems include Sensor Disk Query sensors and Sensor storage, and Query want to perform Millions of data elements arrive queries on per second Query recently arrived data using indexes. recent data. Sensor 6.172 —How Fractal Trees Work 4 The Data Indexing Problem • Data arrives in one order (say, sorted by the time of the observation). • Data is queried in another order (say, by URL or location). Sensor Query Sensor Disk Query Sensor Query Millions of data elements arrive per second Query recently arrived data using indexes. Sensor 6.172 —How Fractal Trees Work 5 Why Not Simply Sort? • This is what data Data Sorted by Time warehouses do. • The problem is that you Sort must wait to sort the data before querying it: Data Sorted by URL typically an overnight delay.
    [Show full text]
  • Search Trees for Strings a Balanced Binary Search Tree Is a Powerful Data Structure That Stores a Set of Objects and Supports Many Operations Including
    Search Trees for Strings A balanced binary search tree is a powerful data structure that stores a set of objects and supports many operations including: Insert and Delete. Lookup: Find if a given object is in the set, and if it is, possibly return some data associated with the object. Range query: Find all objects in a given range. The time complexity of the operations for a set of size n is O(log n) (plus the size of the result) assuming constant time comparisons. There are also alternative data structures, particularly if we do not need to support all operations: • A hash table supports operations in constant time but does not support range queries. • An ordered array is simpler, faster and more space efficient in practice, but does not support insertions and deletions. A data structure is called dynamic if it supports insertions and deletions and static if not. 107 When the objects are strings, operations slow down: • Comparison are slower. For example, the average case time complexity is O(log n logσ n) for operations in a binary search tree storing a random set of strings. • Computing a hash function is slower too. For a string set R, there are also new types of queries: Lcp query: What is the length of the longest prefix of the query string S that is also a prefix of some string in R. Prefix query: Find all strings in R that have S as a prefix. The prefix query is a special type of range query. 108 Trie A trie is a rooted tree with the following properties: • Edges are labelled with symbols from an alphabet Σ.
    [Show full text]
  • Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke
    Trees Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke Department of Computer Science & Engineering University of Nebraska|Lincoln Lincoln, NE 68588, USA [email protected] http://cse.unl.edu/~cbourke 2015/01/31 21:05:31 Abstract These are lecture notes used in CSCE 156 (Computer Science II), CSCE 235 (Dis- crete Structures) and CSCE 310 (Data Structures & Algorithms) at the University of Nebraska|Lincoln. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License 1 Contents I Trees4 1 Introduction4 2 Definitions & Terminology5 3 Tree Traversal7 3.1 Preorder Traversal................................7 3.2 Inorder Traversal.................................7 3.3 Postorder Traversal................................7 3.4 Breadth-First Search Traversal..........................8 3.5 Implementations & Data Structures.......................8 3.5.1 Preorder Implementations........................8 3.5.2 Inorder Implementation.........................9 3.5.3 Postorder Implementation........................ 10 3.5.4 BFS Implementation........................... 12 3.5.5 Tree Walk Implementations....................... 12 3.6 Operations..................................... 12 4 Binary Search Trees 14 4.1 Basic Operations................................. 15 5 Balanced Binary Search Trees 17 5.1 2-3 Trees...................................... 17 5.2 AVL Trees..................................... 17 5.3 Red-Black Trees.................................. 19 6 Optimal Binary Search Trees 19 7 Heaps 19
    [Show full text]