View of the Algorithm Will Be Discussed Below to Summarize the Key Points of the Algorithm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

VMAA-Performance-Sta
Revised June 18, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L. -

Petitioner's Exhibit 17
JURC PETITIONER'S EXHIBIT 0.~~.....L--- Petitioner's Exhibit 17 7 TOWN OF CEDAR LAKE Preliminary Engineering Report Cedar Lake Water Utility System Improvements July 2020 Prepared by: !,?.!! !!e.!,~JI ~ •• !.'!!; ru.E.~~ ~ Ph: (219) 844 8680 • Fax: (219) 844 7754 · e-mail: [email protected] Your Vision • Our Focus Table of Contents 1. Project Location ............................................................................................................................................ 6 2. Current Needs ............................................................................................................................................... 6 2.1. Existing System ...................................................................................................................................... 6 2.1.a. Distribution System ....................................................................................................................... 6 2.1.b. Supply System ............................................................................................................................... 7 2.1.c. Storage System ............................................................................................................................. 8 2.1.d. Treatment Systems ....................................................................................................................... 8 2.1.e. Document Needs ......................................................................................................................... -

Event Information
46th NATIONAL INCLUSIVE ATHLETICS CHAMPIONSHIPS 2018 EVENT INFORMATION 1 INTRODUCTION The Singapore Disability Sports Council (SDSC) is pleased to invite all individuals, schools, associations and clubs to participate in the National Inclusive Athletics Championships on 20 and 28 April 2018. 1.1 Objectives: ● Creating opportunities for persons with disability to compete ● Recruiting potential newcomers to the national or national development squads ● Nominating athletes to represent Singapore at major/international competitions 1.2 This Entry Pack contains: ● Event Information ● Registration Form ● Registration for Classification Form ● Protest form 2 GENERAL INFORMATION 2.1 Field (Throws) & Long Jump Events Date: 20 April 2018 (Friday) Venue: Home of Athletics. 52 Stadium Road Singapore 397724 Time: 5:00 pm (Admission). 6:00 pm (Event Start) – 10:00 pm Division: Open Division - 15 years old and above (Born in 2003 or before) Track Events Date: 28 April 2018 (Saturday) Venue: MOE (Evans Road) Stadium. 21 Evans Road Singapore 259366 Time: 5:00 pm (Admission). 6:00 pm (Event Start) – 10:00 pm Division: Open Division - 15 years old and above (Born in 2003 or before) 2.2 Eligibility: - Singaporean or PR - With either Intellectual Impairment / Visual Impairment / Cerebral Palsy / Physical Impairment / Hearing Impairment - With a valid local or international classification status - Competent in their respective events and able to meet the Minimum Qualifying Standards (MQS) (See Annex A: Events & MQS Table) 2.3 Entry Fee: $10.00 per participant (Invoice will be issued upon registration, with payment instructions.) Page 1 of 12 46th NATIONAL INCLUSIVE ATHLETICS CHAMPIONSHIPS 2018 2.4 Registration 23rd March 2018 Deadline: Email completed forms to [email protected]. -

Athletics Classification Rules and Regulations 2
IPC ATHLETICS International Paralympic Committee Athletics Classifi cation Rules and Regulations January 2016 O cial IPC Athletics Partner www.paralympic.org/athleticswww.ipc-athletics.org @IPCAthletics ParalympicSport.TV /IPCAthletics Recognition Page IPC Athletics.indd 1 11/12/2013 10:12:43 Purpose and Organisation of these Rules ................................................................................. 4 Purpose ............................................................................................................................... 4 Organisation ........................................................................................................................ 4 1 Article One - Scope and Application .................................................................................. 6 International Classification ................................................................................................... 6 Interpretation, Commencement and Amendment ................................................................. 6 2 Article Two – Classification Personnel .............................................................................. 8 Classification Personnel ....................................................................................................... 8 Classifier Competencies, Qualifications and Responsibilities ................................................ 9 3 Article Three - Classification Panels ................................................................................ 11 4 Article Four -

SIGNIFICANT INCIDENT SUMMARY BFC #11-179 11/28/2011 to 12/4/2011 LAFD Meeting Date: January 17, 2012 Emergency Public Information Center
SIGNIFICANT INCIDENT SUMMARY BFC #11-179 11/28/2011 TO 12/4/2011 LAFD Meeting Date: January 17, 2012 Emergency Public Information Center INCIDENT DATE INC. TIME ADDRESS COUNCIL INCIDENT TYPE F.S. FIRE COMPANIES TOTAL F/F'S TOTAL R.A.S OUTSIDE AGENCIES F/F INJURIES CIV. FATALITY DOLLAR LOSS TIME TO CONTROL 11/29/2011 11:31 AM 6550 West 80th Street 11 Greater Alarm Structure Fire 005 9 57 3 0 0 $75000 0 hours, 35 min. F/F FATALITY INC. # Arson Fire CIV/INJURY INCIDENT DURATION Playa Del Rey 0482 0 3 2 hours, 55 min. ARSON STRIKES ORVILLE WRIGHT MIDDLE SCHOOL PLAYA DEL REY - A malicious, intentionally set fire struck a local Middle School today, that significantly damaged school property and injured three. The Los Angeles Fire Department was called to 6550 West 80th Street for a reported "Rubbish Fire" at Orville Wright Middle School at 11:31 am on Tuesday, November 29, 2011. First on-scene resources found a freestanding structure on school grounds, with heavy fire showing. School administrators did evacuate the entire campus as a precaution, but not before three individuals (one student, two adults) were treated for smoke inhalation. One patient, an approximate 50 year old female, was transported to a local hospital in "fair" condition with non-life threatening injuries and an unknown, but related illness. The blaze was fully extinguished by 57 Firefighters in just 35 minutes. The LAFD's Arson-Counter-Terrorism Section was dispatched to the school, where they quickly determined this fire to have been "intentionally and maliciously set." Arson Investigators remained for several hours, processing the scene. -

Classification Report
World Para Athletics Classification Master List Summer Season 2017 Classification Report created by IPC Sport Data Management System Sport: Athletics | Season: Summer Season 2017 | Region: Oceania Region | NPC: Australia | Found Athletes: 114 Australia SDMS ID Family Name Given Name Gender Birth T Status F Status P Status Reason MASH 14982 Anderson Rae W 1997 T37 R F37 R-2024 10627 Arkley Natheniel M 1994 T54 C 33205 Ault-Connell Eliza W 1981 T54 C 1756 Ballard Angela W 1982 T53 C 26871 Barty Chris M 1988 T35 R F34 R MRR 1778 Beattie Carlee W 1982 T47 C F46 C 26763 Bertalli James M 1998 T37 R F37 R 17624 Blake Torita W 1995 T38 R-2022 32691 Bounty Daniel M 2001 T38 R-2022 13801 Burrows Thomas M 1990 T20 [TaR] R 29097 Byrt Eliesha W 1988 T20 [TaR] C 32689 Carr Blake M 1994 T20 [HozJ] C F20 N 10538 Carter Samuel M 1991 T54 C 1882 Cartwright Kelly W 1989 T63 C F63 C 29947 Charlton Julie W 1999 T54 C F57 C 1899 Chatman Aaron M 1987 T47 C 29944 Christiansen Mitchell M 1997 T37 R-2025 26224 Cleaver Erin W 2000 T38 R-2022 19971 Clifford Jaryd M 1999 T12 R-2023 F12 R-2023 29945 Colley Tamsin W 2002 T36 R-2023 F36 R-2020 1941 Colman Richard M 1984 T53 C 26990 Coop Brianna W 1998 T35 R-2022 19721 Copas Stacey W 1978 T51 R F52 C 32680 Crees Dayna W 2002 F34 R-2022 29973 Crombie Cameron M 1986 F38 R-2022 19964 Cronje Jessica W 1998 T37 R F37 R IPC Sport Data Management System Page 1 of 4 6 October 2021 at 07:08:42 CEST World Para Athletics Classification Master List Summer Season 2017 19546 Davidson Brayden M 1997 T36 R-2022 1978 Dawes Christie W -

Publication 938 8:13 - 6-SEP-2007
Userid: ________ DTD TIP04 Leadpct: 0% Pt. size: 7 ❏ Draft ❏ Ok to Print PAGER/SGML Fileid: D:\Users\4h5fb\documents\Epicfiles\P938QF4_2006a.sgm (Init. & date) Page 1 of 224 of Publication 938 8:13 - 6-SEP-2007 The type and rule above prints on all proofs including departmental reproduction proofs. MUST be removed before printing. Publication 938 Introduction (Rev. September 2007) This publication contains directories relating to Cat. No. 10647L Department real estate mortgage investment conduits of the (REMICs) and collateralized debt obligations Treasury (CDOs). The directory for each calendar quarter Real Estate is based on information submitted to the IRS Internal during that quarter. This publication is only avail- Revenue able on the Internet. Service Mortgage For each quarter, there is a directory of new REMICs and CDOs, and a section containing amended listings. You can use the directory to Investment find the representative of the REMIC or the is- suer of the CDO from whom you can request tax information. The amended listing section shows Conduits changes to previously listed REMICs and CDOs. The update for each calendar quarter will be added to this publication approximately six (REMICs) weeks after the end of the quarter. Other information. Publication 550, Invest- ment Income and Expenses, discusses the tax Reporting treatment that applies to holders of these invest- ment products. For other information about REMICs, see sections 860A through 860G of Information the Internal Revenue Code (IRC) and any regu- lations issued under those sections. After 1995. After the November 1995 edi- (And Other tion, Publication 938 is only available electroni- cally. -

(VA) Veteran Monthly Assistance Allowance for Disabled Veterans
Revised May 23, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L. -

Wadsworth Center Therapeutic Substance Monitoring Proficiency Testing – January 25, 2010
New York State Department of Health – Wadsworth Center Therapeutic Substance Monitoring Proficiency Testing – January 25, 2010 Summary of Participant Performance (Mean and Standard Deviation) Acetaminophen (mg/L) Specimen: T31 Specimen: T32 Specimen: T33 Specimen: T34 Specimen: T35 Number [Code] Instrument or Reagent System -------------- -------------- -------------- -------------- -------------- ------- ------------------------------------- 82.35 ± 4.01 152.62 ± 7.45 122.58 ± 6.70 63.66 ± 3.11 39.05 ± 2.00 n = 221 [---] All Methods & Instruments 78.1 146.4 117.0 60.1 38.7 [---] Weigh-in Value <Instruments> 73.87 ± 1.13 138.45 ± 2.30 110.35 ± 1.58 56.50 ± 1.22 34.15 ± 0.41 n = 4 [ABH] Abbott Architect 81.75 ± 4.18 156.47 ± 5.12 123.08 ± 9.23 63.00 ± 3.12 40.20 ± 2.58 n = 11 [ABB] Abbott AxSym 79.58 ± 4.86 152.37 ± 7.67 123.34 ± 8.61 64.06 ± 3.94 37.95 ± 1.13 n = 5 [ABG] Abbott TDX FLX 77.36 ± 3.86 142.43 ± 5.65 113.67 ± 5.63 58.75 ± 3.11 35.29 ± 2.46 n = 9 [OLC] Beckman Coulter AU Chemistry System 87.03 ± 2.47 157.54 ± 4.93 127.76 ± 4.17 67.76 ± 1.84 39.33 ± 4.04 n = 4 [BCS] Beckman Coulter CX 81.14 ± 4.13 152.48 ± 5.80 122.09 ± 5.42 63.34 ± 3.33 39.13 ± 3.42 n = 12 [BCX] Beckman Coulter LX-20 82.05 ± 4.32 151.03 ± 5.65 120.47 ± 3.76 63.02 ± 2.52 38.90 ± 2.51 n = 10 [BCG] Beckman Coulter UniCel DxC 600 81.32 ± 4.17 151.70 ± 6.90 124.22 ± 4.69 63.60 ± 3.16 38.44 ± 2.62 n = 15 [BCH] Beckman Coulter UniCel DxC 800 85.53 ± 0.84 161.69 ± 1.41 128.71 ± 1.92 66.28 ± 1.50 39.82 ± 0.40 n = 4 [JJE] Ortho Vitros 250/350/950 86.35 ± 1.91 161.12 -
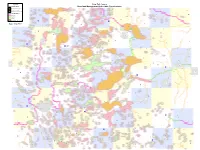
Otter Tail County Shoreland Management District and Classifications
Legend Otter Tail County Frazee Lake Classifications Shoreland Management District and Classifications r e v i BUCK PELICAN R FISCHER n BOOT a General Development c GRAHAM R 6 5 4 3 2 T20 li DEAD e 1 e d " 6 5 P MURPHY e 4 3 COOKCSOOKS SIX y 1 DUCK 2 1 6 5 4 3 2 1 e 4 3 2 LITTLE PELICAN 6 5 4 6 5 4 3 2 1 6 R 5 4 3 2 1 6 5 3 2 1GRAY 6 5 4 3 2 1 T13 i HAND FIVE " v er Natural Environment BURTON INDIAN T75 HOLBROOK " PELICAN FAIRY T17 SCHRAMS Recreational Development 7 " WIMER SILVER 8 9 10 11 12 7 8 9 7 8 9 10 11 12 10 11 12 10 11 12 7 8 9 10 7 T189 9 SCALP 8 9 10 11 12KEYES 7 8 9 10 11 12 7 8 9 10 11 12 7 11 12 " C a River Classifications t THOMPSON MUD C 31 TEE GERTRUDE 70 T r T 9 IDA THOMPSON 148 23 T " T e " T LEEK " BASS " e " BEAR k Agriculture 18 17 LITTLE ROSE (MUD) 16 15 14 13 18 17 T 16 oa 13 15 14 13 18 17 16 15 14 13 d 16 18 17 16 15 14 18 17 16 15 14 13 18 17 16 15 14 51 13 Ri 18 17 16 15 14 13 18 17 15 14 13 Redeye River FISH "T ver MUD Transition RICE ROSE JIM 4 EDNA 62 P T 146 SEIM T BUSINGER T HARRISON e " " BRADBURY " l ELBOW 19 20 i 21 22 23 c Tributary 24 19 a 20 21 n 22 23 24 19 20 21 22 VER2G3AS 24 21 22 23 24 RANKLE 19 19 20 21 22 23 24 19 20 R 20 21 24 TAMARAC 22 23 24 19 20 21 60 22 23 24 19 20 21 22 23 i T v " MUD e 1000' Lakeshore Boundary ?A@34 r HOOK COFFEE ?A@228 30 P2E9TE 28 27 26 Vergas 10 25 30 29 28 ¤£ 27 26 25 30 29 28 27 Ot 27 26 25 26 25 30 29 28 ter 25 30 29 28 27 26 25 30 29 28 LAWRENCE LONG 27 26 25 30 29 28 T 27 26 25 30 29 28 27 26 ail Ri T53 ver " FRANKLIN 130 Date: 7/24/2017 T 36 T8 MAPLE T9 " -

English Federation of Disability Sport National Junior Athletics Information and Standards
English Federation of Disability Sport National Junior Athletics Information and standards 1 Contents Introduction 3 EFDS track groupings 4 EFDS field groupings 5 Events available 6 National field weights 8 National standards track 11 National standard field 13 2 Introduction This booklet has been produced with the intention of enabling athletes, coaches, teachers and parents to compare EFDS Profiles and Athletics Groupings with IPC Athletics Classes, the enclosed information is a guide for EFDS Events and IS NOT AN IPC CLASSIFICATION. You can find out further information on classification using the following links: www.englandathletics.org/disability-athletics/eligibility-and-classification UK Classification will allow athletes to: - Enter Parallel Success events across UK - Register times on the UK Rankings (www.thepowerof10.info) - Be eligible for Sainsbury’s School Games selection - Receive monthly Paralympic newsletter from British Athletics For athletes interested in joining an athletics club and seeking a UK Classification please contact. - Shelley Holroyd (England North & East) [email protected] - Job King (England Midlands & South) [email protected] Or complete the following online form. www.englandathletics.org/parallelsuccess The document contains information regarding the events available to athletes, the specific weights for throwing implements relevant to the EFDS Field and Age Groups as well as the qualifying standards for the National Junior Athletics Championships. Our aim is to provide as much information and support as possible so that athletes, regardless of their ability can continue to participate within the sport of athletics. We are committed to delivering multi- disability events that cater for both the needs of the disability community and the relevant NGB pathway for talented athletes. -

1/24 Eliminations / 2020-08-03 Archery Yumenoshima Park Archery Field 2021-08-28 09:00 14:55 Changed the Time from "14:00" to "14:55"
Competition Schedule: The Event Line-up for Each Session of the Tokyo 2020 Paralympic Games change log Change date SPORT(DISCIPLINE) VENUE DATE START TIME END TIME EVENT Change log Men's Individual Compound Open: 1/24 Eliminations / 2020-08-03 Archery Yumenoshima Park Archery Field 2021-08-28 09:00 14:55 Changed the time from "14:00" to "14:55". Men's Individual Compound Open: 1/16 Eliminations Mixed Team W1: 1/8 Eliminations / Mixed Team W1: Quarterfinals / Mixed Team W1: Semifinals / Changed the time from "17:00-21:25" to "17:30- 2020-08-03 Archery Yumenoshima Park Archery Field 2021-08-28 17:30 21:55 Mixed Team W1: Bronze Medal Match / 21:55". Mixed Team W1: Gold Medal Match / Mixed Team W1: Victory Ceremony Women's Individual Compound Open: 1/16 Eliminations / 2020-08-03 Archery Yumenoshima Park Archery Field 2021-08-29 09:00 14:10 Changed the time from "13:55" to "14:10". Mixed Team Compound Open: 1/8 Eliminations Mixed Team Compound Open: Quarterfinals / Mixed Team Compound Open: Semifinals / Changed the time from "17:00-21:25" to "17:30- 2020-08-03 Archery Yumenoshima Park Archery Field 2021-08-29 17:30 20:35 Mixed Team Compound Open: Bronze Medal Match / 20:35". Mixed Team Compound Open: Gold Medal Match / Mixed Team Compound Open: Victory Ceremony Women's Individual Compound Open: 1/8 Eliminations / Women's Individual Compound Open: Quarterfinals / Women's Individual Compound Open: Semifinals / 2020-08-03 Archery Yumenoshima Park Archery Field 2021-08-30 09:00 14:15 Changed the time from "13:25" to "14:15".