Quotients of Toric Varieties by the Action of a Subtorus, Preprint, Warsaw (1998)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fan V/Stol Aircraft
c' I4 FAN V/STOL AIRCRAFT By M. 0. McKinney and W. A. Newsom NASA Langley Research Center Langley Station, Hampton, Va. Presented at tke New York Academy of Scienees International Congress of Subsonic Aeronautics $- $- CFSTI PRICE(S) $ Mcrofiche (MF) * 6c ff 653 July65 New York, New York April 3-6, 1967 " FANV/STOL AIRCRAFT By M. 0. McKinney and W. A. Newsom NASA Langley Research Center SUMMARY This paper points out some of the fundamental characteristics of fan- powered V/STOL aircraft and demonstrates with various test data how these fundamental characteristics show up in the characteristics of various particular configurations. Since most of the experience with fan-powered V/STOL configu- rations has been gained in wind tunnels, the emphasis in the paper is on aero- dynamics although some operational data from flight tests are presented. INTRODUCTION There have been several fan-powered V/STOL aircraft built and a consid- erably larger number of fan-powered V/STOL aircraft configurations have been tested in wind tunnels; but the experimental work has not been systematic enough, and the theoretical work has not been complete enough to permit deter- mination of the characteristics of arbitrary configurations. The purpose of the present paper is to provide an aid for the understanding of the aerodynamic characteristics of such aircraft by pointing out some of the fundamental char- acteristics of such aircraft and demonstrating with various test data how these fundamental characteristics show up in the characteristics of particular con- figurations as observed in wind-tunnel and flight tests. Since the wind-tunnel experience is much greater than the flight experience, the main emphasis will be on characteristics observed in wind-tunnel tests. -

Visual Metaphors on Album Covers: an Analysis Into Graphic Design's
Visual Metaphors on Album Covers: An Analysis into Graphic Design’s Effectiveness at Conveying Music Genres by Vivian Le A THESIS submitted to Oregon State University Honors College in partial fulfillment of the requirements for the degree of Honors Baccalaureate of Science in Accounting and Business Information Systems (Honors Scholar) Presented May 29, 2020 Commencement June 2020 AN ABSTRACT OF THE THESIS OF Vivian Le for the degree of Honors Baccalaureate of Science in Accounting and Business Information Systems presented on May 29, 2020. Title: Visual Metaphors on Album Covers: An Analysis into Graphic Design’s Effectiveness at Conveying Music Genres. Abstract approved:_____________________________________________________ Ryann Reynolds-McIlnay The rise of digital streaming has largely impacted the way the average listener consumes music. Consequentially, while the role of album art has evolved to meet the changes in music technology, it is hard to measure the effect of digital streaming on modern album art. This research seeks to determine whether or not graphic design still plays a role in marketing information about the music, such as its genre, to the consumer. It does so through two studies: 1. A computer visual analysis that measures color dominance of an image, and 2. A mixed-design lab experiment with volunteer participants who attempt to assess the genre of a given album. Findings from the first study show that color scheme models created from album samples cannot be used to predict the genre of an album. Further findings from the second theory show that consumers pay a significant amount of attention to album covers, enough to be able to correctly assess the genre of an album most of the time. -
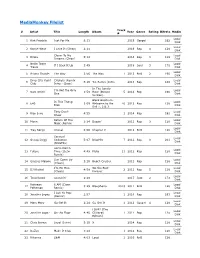
Mediamonkey Filelist
MediaMonkey Filelist Track # Artist Title Length Album Year Genre Rating Bitrate Media # Local 1 Kirk Franklin Just For Me 5:11 2019 Gospel 182 Disk Local 2 Kanye West I Love It (Clean) 2:11 2019 Rap 4 128 Disk Closer To My Local 3 Drake 5:14 2014 Rap 3 128 Dreams (Clean) Disk Nellie Tager Local 4 If I Back It Up 3:49 2018 Soul 3 172 Travis Disk Local 5 Ariana Grande The Way 3:56 The Way 1 2013 RnB 2 190 Disk Drop City Yacht Crickets (Remix Local 6 5:16 T.I. Remix (Intro 2013 Rap 128 Club Intro - Clean) Disk In The Lonely I'm Not the Only Local 7 Sam Smith 3:59 Hour (Deluxe 5 2014 Pop 190 One Disk Version) Block Brochure: In This Thang Local 8 E40 3:09 Welcome to the 16 2012 Rap 128 Breh Disk Soil 1, 2 & 3 They Don't Local 9 Rico Love 4:55 1 2014 Rap 182 Know Disk Return Of The Local 10 Mann 3:34 Buzzin' 2011 Rap 3 128 Macc (Remix) Disk Local 11 Trey Songz Unusal 4:00 Chapter V 2012 RnB 128 Disk Sensual Local 12 Snoop Dogg Seduction 5:07 BlissMix 7 2012 Rap 0 201 Disk (BlissMix) Same Damn Local 13 Future Time (Clean 4:49 Pluto 11 2012 Rap 128 Disk Remix) Sun Come Up Local 14 Glasses Malone 3:20 Beach Cruiser 2011 Rap 128 (Clean) Disk I'm On One We the Best Local 15 DJ Khaled 4:59 2 2011 Rap 5 128 (Clean) Forever Disk Local 16 Tessellated Searchin' 2:29 2017 Jazz 2 173 Disk Rahsaan 6 AM (Clean Local 17 3:29 Bleuphoria 2813 2011 RnB 128 Patterson Remix) Disk I Luh Ya Papi Local 18 Jennifer Lopez 2:57 1 2014 Rap 193 (Remix) Disk Local 19 Mary Mary Go Get It 2:24 Go Get It 1 2012 Gospel 4 128 Disk LOVE? [The Local 20 Jennifer Lopez On the -

Slang Dalam Lirik-Lirik Lagu Chris Brown
SLANG DALAM LIRIK-LIRIK LAGU CHRIS BROWN JURNAL SKRIPSI Diajukan Sebagai Salah Satu Syarat Untuk Mencapai Gelar Sarjana Sastra Oleh : DEVIYANTI WINDA 13091102075 Jurusan Sastra Inggris UNIVERSITAS SAM RATULANGI FAKULTAS ILMU BUDAYA MANADO 2017 ABSTRACT This skripsi is entitled “SLANG DALAM LAGU-LAGU CHRIS BROWN”. The aims of this research are to analyze, identify and classify the words that use slang words of Chris Brown’s songs. The purpose of this research is to analyze the types of slang by using song lyrics of Chris Brown’s songs. The research uses descriptive method. The theory of Elissa Matiello (2008) and Leech theory (1998) are used in this research. The data were collected by listening to 10 songs by Chris Brown and reading the lyrics of the songs. The result of this research shows that there are four forms of slang in Chris Brown’s songs namely, blending, clipping, copy reduplicatives, variation. The results of this research also shows that there are four meanings of slang in Chris Brown’s songs namely, conceptual meaning with 63 data, connotative meaning with 2 data, thematic meaning with 2 data, social meaning with 2 data. ______________________________________________ Key words: Slang,Meaning, Chris Brown’s songs, Sociolinguistics. PENDAHULUAN Latar Belakang Bahasa adalah simbol dari sistem suara ucapan yang digunakan sebagai alat untuk berkomunikasi oleh pemakainya. Bahasa itu sendiri berfungsi sebagai alat komunikasi dan merupakan cara paling paling lengkap dan efektif untuk menyampaikan ide, pesan, niat, dan opini kepada orang lain. Ilmu yang mempelajari bahasa disebut linguistik. Menurut Martinet (1987:19) linguistik adalah ilmu yang mengambil bahasa sebagai objek kajiannya. -

La Loi Sur Les Radars Seravotéeavantl'été
MARDI 24 FÉVRIER 2015 N°1700 La loi sur les radars Luxembourg 4 La culture se partagera 13,31 millions d’euros sera votée avant l'été Encore dans l'attente de l'avis du sions publiques ont déjà été lancées. Conseil d’État sur le projet d’installa- Sauf accident, les premiers radars au- tion de radars automatiques, le gou- tomatiques fixes (une vingtaine) pour- vernement fait le forcing pour que la ront être installés avant les départs en loi soit votée avant l'été. Les soumis- vacances d’été. PAGE 3 ...................................................................................................................................................... «Birdman» a survolé les Oscars Économie 10 La situation est vraiment grave pour Cargolux Sports 25 Juve-Dortmund et City- Barça, deux gros chocs! J.K. Simmons, Patricia Arquette, Julianne Moore et Eddie Redmayne ont été récompensés pour leur performance d'acteur. Météo 28 La comédie noire «Birdman» a tants sur le droit des femmes et favori avec neuf nominations. Il MATIN APRÈS-MIDI décroché l’oscar du meilleur film des minorités. «Birdman», pro- en a finalement remporté qua- et dominé une 87e soirée des Os- duit, écrit et réalisé par le Mexi- tre, comme «The Grand Buda- -1°6° cars ponctuée de messages mili- cain Alejandro Iñárritu, partait pest Hotel». PAGE 18 2 Actu MARDI 24 FÉVRIER 2015 / WWW.LESSENTIEL.LU Un bébé décède La neige-surprise provoque de la rougeole BERLIN - Un bébé de 18 mois est décédé de la rougeole le chaos sur les routes mercredi dernier à Berlin, premier décès répertorié alors LUXEMBOURG - La que la maladie frappe en Alle- neige-surprise d'hier magne depuis l’automne, ont matin a causé pas mal annoncé, hier, les autorités sanitaires de la capitale. -

Billboard Magazine
The AMY NOBODY KNEW A new documentary reveals fresh details on the shocking, heartbreaking life, death and enduring legacy of Winehouse. Says Sam Smith: “She’s the reason why I sing” July 4, 2015 | billboard.com DOUBLE ISSUE Display until July 17, 2015 KABOOM! AFTERMATH OF APPLE AND TAYLOR SWIFT UK £5.50 WorldMags.net WorldMags.net WorldMags.net pmoqiin Is Kelsea Ballerini The Next Carrie LAURA FARR/ADMEDIA Underwood? IRL POWER REIGNS SUPREME — AT LAST — ON country radio. Kelsea Ballerini is the first woman to send a debut single to No. 1 on Billboard’s Country G Airplay chart (see page 65) in more than nine years as “Love Me Like You Mean It” (from her debut album The First Time, released in May on indie label Black River) rises 2-1. On the Billboard Hot 100, the track bullets at No. 46. It’s the first career- opening single by a solo female to crown Country Airplay since Carrie Underwood’s “Jesus, Take the Wheel” in 2006, released to country radio after she won American Idol in 2005. LC and Nielsen Music, Inc.LC All rights reserved. “I’ve been writing songs since I was 12, and so many times I’ve wondered if I was good at it,” Ballerini, 21, tells Billboard. “To see it work is so reassuring that this is what I’m supposed to be doing.” Black River also celebrates its first Country Airplay No. 1. “It’s a huge day for us as an independent record label,” says CEO Gordon Kerr. “So many people have embraced us. -

Chris Brown One Hell of a Nite Tour (FINAL)
CHRIS BROWN ANNOUNCES ONE HELL OF A NITE TOUR – Kid Ink, Omarion, Fetty Wap & Teyana Taylor To Join 2015 Summer Amphitheatre Tour As Special Guests – – Tickets On Sale Starting Friday, June 12 at LiveNation.com – LOS ANGELES (June 8, 2015) – Multi-platinum selling artist Chris Brown today announced a headlining summer amphitheatre tour. Produced by Live Nation and Haymon Events, the ONE HELL OF A NITE TOUR kicks off on August 12 at Sprint Center in Kansas City, Mo. and will take the acclaimed performer to 25 cities throughout the U.S. including shows in Chicago, Detroit, Boston, Miami, Atlanta, Dallas and San Diego. Kid Ink , Omarion , Fetty Wap and Teyana Taylor will join Chris on the summer tour as special guests. A full list of tour dates is below. A Citi® cardmember pre-sale begins Tuesday, June 9 through Citi's Private Pass® Program. For complete pre-sale details, visit www.citiprivatepass.com. Tickets for the general public go on sale starting Friday, June 12 at www.livenation.com. GRAMMY Award®-winning singer/songwriter Chris Brown made his sixth #1 album entry on the Billboard R&B/Hip-Hop chart with his latest release X (RCAS Records). The album also debuted at #2 on Billboard's Top Albums chart, marking his sixth album debut within the Top Ten. X sold over 140,000 units in its first week while Spotify streams of the album continue to rise. Earlier this year, Brown released his first collaborate studio album, Fan of a Fan: The Album, with Tyga. The album debuted in the Top 10 on the Billboard 200. -

AA-Postscript 2.Qxp:Layout 1
36 TUESDAY, AUGUST 25, 2015 LIFESTYLE Gossip hris Brown has named his new album after his daughter. The 26- Sting’s guitarist: The Police Cyear-old star is expected to release his seventh solo studio album later this year and revealed he has named the collection ‘Royalty’, after the tot who he announced he was the father to back in April. should have stayed together Announcing the news on Twitter, he simply wrote: “MY NEW ALBUM ting’s guitarist Andy Summers thinks The WILL BE NAMED “ROYALTY.” (sic)” The LP follows his collaborative Police shouldn’t have broke up. The 72-year- release with Tyga ‘Fan of a Fan: The Album’ earlier this year and will be S old rocker - who replaced original guitarist his first solo release since 2014’s ‘X’, which featured hit singles ‘Loyal’ Henri Padovani in the band fronted by the and ‘New Flame’. The hip hop star - who recently collaborated with Rita ‘Roxanne’ singer - revealed that numerous fights Ora for her raunchy single ‘Body On Me’ - has not yet revealed further caused them to disband and Sting to pursue a solo details about the collection, although his former flame Rihanna is career but he believes that they should have stayed reportedly desperate to be involved. A source revealed: “Chris gets together. He said: “I think what we should have nothing but cool points from Ri for naming his new album Royalty! done was probably take two years off, gone away That’s so sweet and a testament of how much he loves and honors his naming album and then come back.”But it didn’t play out that way little girl. -

Entertainment Business Supplemental Information Fiscal Year and Three Months Ended March 31, 2016
Entertainment Business Supplemental Information Fiscal year and three months ended March 31, 2016 April 28, 2016 Sony Corporation Pictures Segment 1 ■ Pictures Segment Aggregated U.S. Dollar Information 1 ■ Motion Pictures 1 - Motion Pictures Box Office for films released in North America - Select films to be released in the U.S. - Top 10 DVD and Blu-rayTM titles released - Select DVD and Blu-rayTM titles to be released ■ Television Productions 4 - Television Series with an original broadcast on a U.S. network - Television Series with a new season to premiere on a U.S. network - Select Television Series in U.S. off-network syndication - Television Series with an original broadcast on a non-U.S. network ■ Media Networks 6 - Television and Digital Channels Music Segment 8 ■ Recorded Music 8 - Recorded Music Revenue breakdown of physical, digital and other revenues - Top 10 best-selling recorded music releases - Upcoming releases ■ Music Publishing 9 - Number of songs in the music publishing catalog owned and administered as of March 31, 2016 Cautionary Statement Statements made in this supplemental information with respect to Sony’s current plans, estimates, strategies and beliefs and other statements that are not historical facts are forward-looking statements. Forward-looking statements include, but are not limited to, those statements using such words as “may,” “will,” “should,” “plan,” “expect,” “anticipate,” “estimate” and similar words, although some forward- looking statements are expressed differently. Sony cautions investors that a number of important risks and uncertainties could cause actual results to differ materially from those discussed in the forward-looking statements, and therefore investors should not place undue reliance on them. -
Chris Brown - Indigo Free Mp3 Download Download Album Chris Brown – Indigo Zip
chris brown - indigo free mp3 download Download Album Chris Brown – Indigo Zip. DOWNLOAD FULL ALBUM Chris Brown – Indigo ZIP / MP3. DOWNLOAD FREE ZIP ALBUM Chris Brown – Indigo Zip MP3 2019. This tracklist is unconfirmed. It is compiled of recent singles, snippets, and song titles sourced from streaming services, PRO’s, and social media. It is purely speculative and has not been confirmed by the artist. We will update this tracklist as more information comes to light. ndigo is Chris’ upcoming ninth studio Album and the follow up to October 2017’s Heartbreak on a Full Moon. The album has been teased as far back as July 2018 when Chris got the words “Indigo” tattooed on his face.The album was preceded by three singles: the R&B-centered “Undecided” and “Back to Love,” and club track “Wobble Up” which features G-Eazy and frequent collaborator Nicki Minaj. In early May 2019, Chris revealed the album’s featured artists in a series of Instagram stories. Guest features include Tyga, Justin Bieber, Drake and Lil Wayne. On May 5th, 2019, his 30th birthday, Chris revealed that the album contains 30 songs to coincide with his age. On May 14th, Chris revealed the official album artwork for the album and that alike Heartbreak on a Full Moon , it will be a double album. Read Chris Brown’s Bio. Christopher Maurice Brown is an American singer, songwriter, dancer and actor. Born in Tappahannock, Virginia, he was involved in his church choir and several local talent shows from a young age. Having signed with Jive Records in 2004, Brown released his self-titled debut studio album the following year. -
Chris Brown Fan of a Fan (The Album) Mp3, Flac, Wma
Chris Brown Fan Of A Fan (The Album) mp3, flac, wma DOWNLOAD LINKS (Clickable) Genre: Hip hop Album: Fan Of A Fan (The Album) Country: Europe Released: 2015 Style: Pop Rap, RnB/Swing MP3 version RAR size: 1961 mb FLAC version RAR size: 1359 mb WMA version RAR size: 1695 mb Rating: 4.4 Votes: 269 Other Formats: DMF TTA MP3 AHX ASF MMF MPC Tracklist Hide Credits 1 Westside Nothin' Like Me 2 Featuring – Ty Dolla $ign* 3 Ayo 4 Girl You Loud 5 Remember Me I Bet 6 Featuring – 50 Cent D.G.I.F.U. 7 Featuring – Pusha T 8 Better Lights Out 9 Featuring – Fat Trel Real One 10 Featuring – Boosie Badazz B****es N Marijuana 11 Featuring – Schoolboy Q 12 She Goin' Up Companies, etc. Phonographic Copyright (p) – RCA Records Copyright (c) – RCA Records Phonographic Copyright (p) – Young Money Entertainment Copyright (c) – Young Money Entertainment Phonographic Copyright (p) – Cash Money Records Copyright (c) – Cash Money Records Distributed By – Sony Music Entertainment Barcode and Other Identifiers Barcode: 0888750560629 Label Code: LC00316 Other versions Category Artist Title (Format) Label Category Country Year RCA, Cash Money Chris Brown X Chris Records, Young Money Tyga - Fan Of A 88875070012 Brown X Entertainment, CBE 88875070012 Europe 2015 Fan (The Album) Tyga Entertainment, Black (CD, Album, Dlx) Pyramid, Sony Music RCA, Cash Money Chris Brown X Chris Records, Young Money Tyga - Fan Of A 88875-05607-2 Brown X Entertainment, CBE 88875-05607-2 US 2015 Fan (The Album) Tyga Entertainment, Black (CD, Album) Pyramid, Sony Music RCA, Cash Money Chris -

Im on It Tyga
Im on it tyga click here to download [Tyga] I'm on it, I'm on it. I'm on it, I'm on it. If we talkin' bout money bitch [Tyga - Verse 1] Snap back chiller gold chain nigga snaps no tigger, tyga bitches. I'm On One Lyrics: All these niggas stealing swag / I've been getting tats since I was fourteen / Tell my bitch throw it in the bag / Twenty-two for the Balmain jeans . View the Lil Wayne lyrics for the song I'm On It with Tyga. Discover releases, reviews, credits, songs, and more about Tyga Feat. Lil Wayne - I'm On It at Discogs. Complete your Tyga Feat. Lil Wayne collection. Find a Tyga Feat. Lil Wayne - I'm On It first pressing or reissue. Complete your Tyga Feat. Lil Wayne collection. Shop Vinyl and CDs. Listen to I'm On It (NO DJ), the new track by Tyga featuring Lil' Wayne which was dropped on Sunday, February 28th, Listen to I'm On It (NO DJ), the la. I'm On It. By Tyga, Lil Wayne. • 1 song, Play on Spotify. 1. I'm On It - Lil Wayne. Featured on I'm On It. We've been waiting on this one since the night before Wayne was scheduled to go to prison and gave a sneak peek when he took Lil Twist and. With a rangy set of friends from Fall Out Boy to Lil Wayne, it was obvious from the start that Tyga was not your everyday rapper from Compton. After recording a.