Quantnet: Transferring Learning Across Trading Strategies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
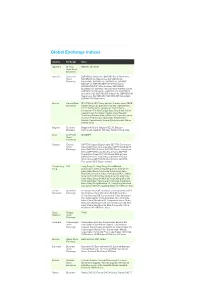
Global Exchange Indices
Global Exchange Indices Country Exchange Index Argentina Buenos MERVAL, BURCAP Aires Stock Exchange Australia Australian S&P/ASX All Ordinaries, S&P/ASX Small Ordinaries, Stock S&P/ASX Small Resources, S&P/ASX Small Exchange Industriials, S&P/ASX 20, S&P/ASX 50, S&P/ASX MIDCAP 50, S&P/ASX MIDCAP 50 Resources, S&P/ASX MIDCAP 50 Industrials, S&P/ASX All Australian 50, S&P/ASX 100, S&P/ASX 100 Resources, S&P/ASX 100 Industrials, S&P/ASX 200, S&P/ASX All Australian 200, S&P/ASX 200 Industrials, S&P/ASX 200 Resources, S&P/ASX 300, S&P/ASX 300 Industrials, S&P/ASX 300 Resources Austria Vienna Stock ATX, ATX Five, ATX Prime, Austrian Traded Index, CECE Exchange Overall Index, CECExt Index, Chinese Traded Index, Czech Traded Index, Hungarian Traded Index, Immobilien ATX, New Europe Blue Chip Index, Polish Traded Index, Romanian Traded Index, Russian Depository Extended Index, Russian Depository Index, Russian Traded Index, SE Europe Traded Index, Serbian Traded Index, Vienna Dynamic Index, Weiner Boerse Index Belgium Euronext Belgium All Share, Belgium BEL20, Belgium Brussels Continuous, Belgium Mid Cap, Belgium Small Cap Brazil Sao Paulo IBOVESPA Stock Exchange Canada Toronto S&P/TSX Capped Equity Index, S&P/TSX Completion Stock Index, S&P/TSX Composite Index, S&P/TSX Equity 60 Exchange Index S&P/TSX 60 Index, S&P/TSX Equity Completion Index, S&P/TSX Equity SmallCap Index, S&P/TSX Global Gold Index, S&P/TSX Global Mining Index, S&P/TSX Income Trust Index, S&P/TSX Preferred Share Index, S&P/TSX SmallCap Index, S&P/TSX Composite GICS Sector Indexes -

Final Report Amending ITS on Main Indices and Recognised Exchanges
Final Report Amendment to Commission Implementing Regulation (EU) 2016/1646 11 December 2019 | ESMA70-156-1535 Table of Contents 1 Executive Summary ....................................................................................................... 4 2 Introduction .................................................................................................................... 5 3 Main indices ................................................................................................................... 6 3.1 General approach ................................................................................................... 6 3.2 Analysis ................................................................................................................... 7 3.3 Conclusions............................................................................................................. 8 4 Recognised exchanges .................................................................................................. 9 4.1 General approach ................................................................................................... 9 4.2 Conclusions............................................................................................................. 9 4.2.1 Treatment of third-country exchanges .............................................................. 9 4.2.2 Impact of Brexit ...............................................................................................10 5 Annexes ........................................................................................................................12 -

Morningstar Indexes Correlation
Morningstar Indexes Correlation Learn More Morningstar Indexes capture a complete set of global investment opportunities, as demonstrated by their high degree indexes.morningstar.com of correlation to the industry’s major indexes. Each Morningstar Index can be used as discrete building blocks for Contact Us asset allocation and portfolio construction analysis. [email protected] North America +1 312 384 3735 EMEA +44 20 3194 1082 Morningstar Index 3rd Party Index Correlation Australia +61 2 9276 4446 Hong Kong +65 6340 1285 Equity Japan +813 5511 7580 US Style 10 yr Korea +82 2 3771 0721 Morningstar US Large Core MSCI US Large Cap 300 0.98 Singapore +65 6340 1285 Russell 1000 TR USD 0.98 S&P 500 TR USD 0.99 Morningstar US Large Growth MSCI US Large Cap Growth 0.99 S&P 500 Growth TR USD 0.98 Russell 1000 Growth TR USD 0.99 Morningstar US Large Value MSCI US Large Cap Value 0.99 Russell 1000 Value TR USD 0.98 S&P 500 Value TR USD 0.98 Morningstar US Mid Core MSCI US Mid Cap 450 1.00 Russell Mid Cap TR USD 0.99 S&P Mid Cap 400 0.99 Morningstar US Mid Growth MSCI US Mid Cap Growth 0.99 S&P Mid Cap 400 Growth 0.98 Russell Mid Cap Growth TR USD 0.99 Morningstar US Mid Value MSCI US Mid Cap Value 0.99 S&P MidCap 400 Value TR USD 0.97 Russell Mid Cap Value TR USD 0.99 Morningstar US Small Core MSCI US Small Cap 1750 1.00 Russell 2000 0.99 S&P SmallCap 600 TR USD 0.98 Morningstar US Small Growth MSCI US Small Cap Growth 0.99 S&P SmallCap 600 Growth 0.99 Russell 2000 Growth TR USD 0.99 Morningstar US Small Value MSCI US Small Cap Value 0.99 Russell 2000 Value TR USD 0.98 S&P SmallCap 600 Value TR USD 0.97 Morningstar US Core Russell 3000 0.99 S&P 500 0.99 Morningstar US Growth Russell 3000 Growth 0.99 S&P United States BMI Growth TR USD 0.99 Morningstar US Value Russell 3000 Value 0.99 S&P United States BMI Value TR USD 0.99 ©2019 Morningstar, Inc. -

The Pricing of Stock Index Futures During the Asian Financial Crisis: Evidence from Four Asian Index Futures Markets”
“The Pricing of Stock Index Futures During the Asian Financial Crisis: Evidence from Four Asian Index Futures Markets” AUTHORS Janchung Wang Janchung Wang (2007). The Pricing of Stock Index Futures During the Asian ARTICLE INFO Financial Crisis: Evidence from Four Asian Index Futures Markets. Investment Management and Financial Innovations, 4(2) RELEASED ON Saturday, 23 June 2007 JOURNAL "Investment Management and Financial Innovations" FOUNDER LLC “Consulting Publishing Company “Business Perspectives” NUMBER OF REFERENCES NUMBER OF FIGURES NUMBER OF TABLES 0 0 0 © The author(s) 2021. This publication is an open access article. businessperspectives.org Investment Management and Financial Innovations, Volume 4, Issue 2, 2007 77 THE PRICING OF STOCK INDEX FUTURES DURING THE ASIAN FINANCIAL CRISIS: EVIDENCE FROM FOUR ASIAN INDEX FUTURES MARKETS Janchung Wang* Abstract Market imperfections are traditionally measured individually. Hsu and Wang (2004) and Wang and Hsu (2006) recently proposed the concept of the degree of market imperfections, which reflects the total effects of all market imperfections between the stock index futures market and its underlying index market when implementing arbitrage activities. This study discusses some useful applications of this concept. Furthermore, Hsu and Wang (2004) developed an imperfect market model for pricing stock index futures. This study further compares the relative pricing perform- ance of the cost of carry and the imperfect market models for four Asian index futures markets (particularly for the Asian crisis period). The evidence indicates that market imperfections are im- portant in determining the stock index futures prices for immature markets and turbulent periods with high market imperfections. Nevertheless, market imperfections are excluded from the cost of carry model. -

Enhancing Liquidity in Emerging Market Exchanges
ENHANCING LIQUIDITY IN EMERGING MARKET EXCHANGES ENHANCING LIQUIDITY IN EMERGING MARKET EXCHANGES OLIVER WYMAN | WORLD FEDERATION OF EXCHANGES 1 CONTENTS 1 2 THE IMPORTANCE OF EXECUTIVE SUMMARY GROWING LIQUIDITY page 2 page 5 3 PROMOTING THE DEVELOPMENT OF A DIVERSE INVESTOR BASE page 10 AUTHORS Daniela Peterhoff, Partner Siobhan Cleary Head of Market Infrastructure Practice Head of Research & Public Policy [email protected] [email protected] Paul Calvey, Partner Stefano Alderighi Market Infrastructure Practice Senior Economist-Researcher [email protected] [email protected] Quinton Goddard, Principal Market Infrastructure Practice [email protected] 4 5 INCREASING THE INVESTING IN THE POOL OF SECURITIES CREATION OF AN AND ASSOCIATED ENABLING MARKET FINANCIAL PRODUCTS ENVIRONMENT page 18 page 28 6 SUMMARY page 36 1 EXECUTIVE SUMMARY Trading venue liquidity is the fundamental enabler of the rapid and fair exchange of securities and derivatives contracts between capital market participants. Liquidity enables investors and issuers to meet their requirements in capital markets, be it an investment, financing, or hedging, as well as reducing investment costs and the cost of capital. Through this, liquidity has a lasting and positive impact on economies. While liquidity across many products remains high in developed markets, many emerging markets suffer from significantly low levels of trading venue liquidity, effectively placing a constraint on economic and market development. We believe that exchanges, regulators, and capital market participants can take action to grow liquidity, improve the efficiency of trading, and better service issuers and investors in their markets. The indirect benefits to emerging market economies could be significant. -

Execution Version
Execution Version GUARANTEED SENIOR SECURED NOTES PROGRAMME issued by GOLDMAN SACHS INTERNATIONAL in respect of which the payment and delivery obligations are guaranteed by THE GOLDMAN SACHS GROUP, INC. (the “PROGRAMME”) PRICING SUPPLEMENT DATED 23rd SEPTEMBER 2020 SERIES 2020-12 SENIOR SECURED EXTENDIBLE FIXED RATE NOTES (the “SERIES”) ISIN: XS2233188510 Common Code: 223318851 This document constitutes the Pricing Supplement of the above Series of Secured Notes (the “Secured Notes”) and must be read in conjunction with the Base Listing Particulars dated 25 September 2019, as supplemented from time to time (the “Base Prospectus”), and in particular, the Base Terms and Conditions of the Secured Notes, as set out therein. Full information on the Issuer, The Goldman Sachs Group. Inc. (the “Guarantor”), and the terms and conditions of the Secured Notes, is only available on the basis of the combination of this Pricing Supplement and the Base Listing Particulars as so supplemented. The Base Listing Particulars has been published at www.ise.ie and is available for viewing during normal business hours at the registered office of the Issuer, and copies may be obtained from the specified office of the listing agent in Ireland. The Issuer accepts responsibility for the information contained in this Pricing Supplement. To the best of the knowledge and belief of the Issuer and the Guarantor the information contained in the Base Listing Particulars, as completed by this Pricing Supplement in relation to the Series of Secured Notes referred to above, is true and accurate in all material respects and, in the context of the issue of this Series, there are no other material facts the omission of which would make any statement in such information misleading. -
Monthly Economic Update
In this month’s recap: the Federal Reserve eases, stocks reach historic peaks, and face-to-face U.S.-China trade talks formally resume. Monthly Economic Update THE MONTH IN BRIEF July was a positive month for stocks and a notable month for news impacting the financial markets. The S&P 500 topped the 3,000 level for the first time. The Federal Reserve cut the country’s benchmark interest rate. Consumer confidence remained strong. Trade representatives from China and the U.S. once again sat down at the negotiating table, as new data showed China’s economy lagging. In Europe, Brexit advocate Boris Johnson was elected as the new Prime Minister of the United Kingdom, and the European Central Bank indicated that it was open to using various options to stimulate economic activity.1 DOMESTIC ECONOMIC HEALTH On July 31, the Federal Reserve cut interest rates for the first time in more than a decade. The Federal Open Market Committee approved a quarter-point reduction to the federal funds rate by a vote of 8-2. Typically, the central bank eases borrowing costs when it senses the business cycle is slowing. As the country has gone ten years without a recession, some analysts viewed this rate cut as a preventative measure. Speaking to the media, Fed Chairman Jerome Powell characterized the cut as a “mid-cycle adjustment.”2 The latest hiring and consumer spending reports from the federal government suggested an economy in good shape, and the latest data on consumer prices showed no great inflation pressure. Employers had expanded their payrolls with 224,000 net new jobs in June, a rebound from the paltry 72,000 gain in May. -

Thomson One Symbols
THOMSON ONE SYMBOLS QUICK REFERENCE CARD QUOTES FOR LISTED SECURITIES TO GET A QUOTE FOR TYPE EXAMPLE Specific Exchange Hyphen followed by exchange qualifier after the symbol IBM-N (N=NYSE) Warrant ' after the symbol IBM' When Issued 'RA after the symbol IBM'RA Class 'letter representing class IBM'A Preferred .letter representing class IBM.B Currency Rates symbol=-FX GBP=-FX QUOTES FOR ETF TO GET A QUOTE FOR TYPE Net Asset Value .NV after the ticker Indicative Value .IV after the ticker Estimated Cash Amount Per Creation Unit .EU after the ticker Shares Outstanding Value .SO after the ticker Total Cash Amount Per Creation Unit .TC after the ticker To get Net Asset Value for CEF, type XsymbolX. QRG-383 Date of issue: 15 December 2015 © 2015 Thomson Reuters. All rights reserved. Thomson Reuters disclaims any and all liability arising from the use of this document and does not guarantee that any information contained herein is accurate or complete. This document contains information proprietary to Thomson Reuters and may not be reproduced, transmitted, or distributed in whole or part without the express written permission of Thomson Reuters. THOMSON ONE SYMBOLS Quick Reference Card MAJOR INDEXES US INDEXES THE AMERICAS INDEX SYMBOL Dow Jones Industrial Average .DJIA Airline Index XAL Dow Jones Composite .COMP AMEX Computer Tech. Index XCI MSCI ACWI 892400STRD-MS AMEX Institutional Index XII MSCI World 990100STRD-MS AMEX Internet Index IIX MSCI EAFE 990300STRD-MS AMEX Oil Index XOI MSCI Emerging Markets 891800STRD-MS AMEX Pharmaceutical Index -

Stock Market Volatility and Return Analysis: a Systematic Literature Review
entropy Review Stock Market Volatility and Return Analysis: A Systematic Literature Review Roni Bhowmik 1,2,* and Shouyang Wang 3 1 School of Economics and Management, Jiujiang University, Jiujiang 322227, China 2 Department of Business Administration, Daffodil International University, Dhaka 1207, Bangladesh 3 Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100080, China; [email protected] * Correspondence: [email protected] Received: 27 March 2020; Accepted: 29 April 2020; Published: 4 May 2020 Abstract: In the field of business research method, a literature review is more relevant than ever. Even though there has been lack of integrity and inflexibility in traditional literature reviews with questions being raised about the quality and trustworthiness of these types of reviews. This research provides a literature review using a systematic database to examine and cross-reference snowballing. In this paper, previous studies featuring a generalized autoregressive conditional heteroskedastic (GARCH) family-based model stock market return and volatility have also been reviewed. The stock market plays a pivotal role in today’s world economic activities, named a “barometer” and “alarm” for economic and financial activities in a country or region. In order to prevent uncertainty and risk in the stock market, it is particularly important to measure effectively the volatility of stock index returns. However, the main purpose of this review is to examine effective GARCH models recommended for performing market returns and volatilities analysis. The secondary purpose of this review study is to conduct a content analysis of return and volatility literature reviews over a period of 12 years (2008–2019) and in 50 different papers. -

FTSE Global Equity Index Series Ground Rules Visit Or E-Mail [email protected]
Ground Rules FTSE Global Equity Index Series v10.9 ftserussell.com An LSEG Business September 2021 Contents 1.0 Introduction .................................................................... 3 2.0 Management Responsibilities ....................................... 5 3.0 FTSE Russell Index Policies ......................................... 7 4.0 Country Inclusion Criteria ............................................. 9 5.0 Inclusion Criteria .......................................................... 11 6.0 Eligible Security Screens ............................................ 12 7.0 Periodic Review of Constituents ................................ 16 8.0 Additions Outside of a Review ................................... 21 9.0 Corporate Actions and Events .................................... 24 10.0 Treatment of Dividends ............................................... 26 11.0 Industry Classification Benchmark (ICB)................... 27 12.0 Algorithm and Calculation Method ............................. 28 Appendix A: Eligible Exchanges and Market Segments .... 29 Appendix B: Eligible Classes of Securities ......................... 34 Appendix C: Calculation Schedule ...................................... 39 Appendix D: Country Additions and Deletions ................... 41 Appendix E: Country Classification ..................................... 43 Appendix F: Country Indices ................................................ 44 Appendix G: FTSE Russell China Share Descriptions ....... 45 Appendix H: Further Information ........................................ -

Family Firms, Chaebol Affiliations, and Corporatesocial Responsibility
sustainability Article Family Firms, Chaebol Affiliations, and Corporate Social Responsibility Haeyoung Ryu 1 and Soo-Joon Chae 2,* 1 Department of Business Administration, Hansei University, Gunpo-si 15852, Korea; [email protected] 2 Department of Business Administration & Accounting, Kangwon National University, Chuncheon-si 24341, Korea * Correspondence: [email protected]; Tel.: +82-33-250-6172 Abstract: This study analyzes the corporate social responsibility (CSR) activities of family-owned firms by investigating public companies in Korea. By nature of their governance structures, which are aligned with the interests of their shareholders and management, family firms are managed from a long-term perspective based on a sense of ownership. While CSR implementation entails investment costs, it ultimately increases firm value by enhancing the firm’s reputation and brand image. As such, family firms are expected to be more active than non-family firms regarding CSR investments. We conducted an empirical analysis based on the Korean Economic Justice Institute Index (KEJI Index) from the Citizens’ Coalition for Economic Justice and found that family firms’ CSR scores were higher than those of non-family firms. This indicates that family firms are relatively more active in their CSR activities, as they are managed from a long-term viewpoint. However, family firms classified as large-scale corporate groups (chaebols) had lower CSR activity levels. This is because when family firms are classified as corporate groups, they can enjoy monopolistic market positioning through their subsidiaries, and are thus more likely to utilize the resources originally required for CSR in other projects that conform to the pursuit of firm interests. -

This Material Was Prepared by Marketingpro, Inc., and Does Not Necessarily Represent the Views of the Presenting Party, Nor Their Affiliates
This material was prepared by MarketingPro, Inc., and does not necessarily represent the views of the presenting party, nor their affiliates. The information herein has been derived from sources believed to be accurate. Please note - investing involves risk, and past performance is no guarantee of future results. Investments will fluctuate and when redeemed may be worth more or less than when originally invested. This information should not be construed as investment, tax or legal advice and may not be relied on for the purpose of avoiding any Federal tax penalty. This is neither a solicitation nor recommendation to purchase or sell any investment or insurance product or service, and should not be relied upon as such. Indices do not incur management fees, costs and expenses, and cannot be invested into directly. All economic and performance data is historical and not indicative of future results. The Dow Jones Industrial Average is a price-weighted index of 30 actively traded blue-chip stocks. The NASDAQ Composite Index is a market-weighted index of all over-the-counter common stocks traded on the National Association of Securities Dealers Automated Quotation System. The Standard & Poor's 500 (S&P 500) is a market-cap weighted index composed of the common stocks of 500 leading companies in leading industries of the U.S. economy. NYSE Group, Inc. (NYSE:NYX) operates two securities exchanges: the New York Stock Exchange (the “NYSE”) and NYSE Arca (formerly known as the Archipelago Exchange, or ArcaEx®, and the Pacific Exchange). NYSE Group is a leading provider of securities listing, trading and market data products and services.