DOCSLIB.ORG

(Anti)Proton Mass and Magnetic Moment

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
(Anti)Proton Mass and Magnetic Moment FFK Conference 2019, Tihany, Hungary Precision measurements of the (anti)proton mass and magnetic moment Wolfgang Quint GSI Darmstadt and University of Heidelberg on behalf of the BASE collaboration spokesperson: Stefan Ulmer 2019 / 06 / 12 BASE – Collaboration • Mainz: Measurement of the magnetic moment of the proton, implementation of new technologies. • CERN Antiproton Decelerator: Measurement of the magnetic moment of the antiproton and proton/antiproton q/m ratio • Hannover/PTB: Laser cooling project, new technologies Institutes: RIKEN, MPI-K, CERN, University of Mainz, Tokyo University, GSI Darmstadt, University of Hannover, PTB Braunschweig C. Smorra et al., EPJ-Special Topics, The BASE Experiment, (2015) WE HAVE A PROBLEM mechanism which created the obvious baryon/antibaryon asymmetry in the Universe is not understood One strategy: Compare the fundamental properties of matter / antimatter conjugates with ultra-high precision CPT tests based on particle/antiparticle comparisons R.S. Van Dyck et al., Phys. Rev. Lett. 59 , 26 (1987). Recent B. Schwingenheuer, et al., Phys. Rev. Lett. 74, 4376 (1995). Past CERN H. Dehmelt et al., Phys. Rev. Lett. 83 , 4694 (1999). G. W. Bennett et al., Phys. Rev. D 73 , 072003 (2006). Planned M. Hori et al., Nature 475 , 485 (2011). ALICE G. Gabriesle et al., PRL 82 , 3199(1999). J. DiSciacca et al., PRL 110 , 130801 (2013). S. Ulmer et al., Nature 524 , 196-200 (2015). ALICE Collaboration, Nature Physics 11 , 811–814 (2015). M. Hori et al., Science 354 , 610 (2016). H. Nagahama et al., Nat. Comm. 8, 14084 (2017). M. Ahmadi et al., Nature 541 , 506 (2017). M. Ahmadi et al., Nature 586 , doi:10.1038/s41586-018-0017 (2018). CERN AD antihydrogen 1S/2S antihydrogen 1S-2S antihydrogen GSHFS Limits on Exotic Physics • Experiments test the Standard Model for exotic interactions 0 ! " #$%&'( ! Dirac equation CPT-odd modifications )*$%&'( !+#$%&'( +! V. A. Kostelecky, N. Russell, → + + 0801.0287v10 (2017). • Boson field exclusively coupling to antimatter Δ , Single particles in Penning traps test the SM at an energy resolution of 10 -24 to 10 -26 GeV sensitive: comparisons of particle/antiparticle magnetic moments in traps Antiprotons – CERN 5.3 MeV antiprotons 25 GeV/c protons 3.5 GeV/c antiprotons -> Degrader -> 1keV Within a production/deceleration -> Electron cooling -> 0.1 eV cycle of 120s + 300s of preparation -> Resistive cooling -> 0.000 3 eV time we bridge 14 orders of -> Feedback cooling -> 0.000 09 eV magnitude The BASE Apparatus at CERN RT: Reservoir trap RT PT CT AT PT: Precision trap CT: Cooling trap AT: Analysis trap HV Electrodes 7 Degrader Spin flip coil Electron gun Pinbase Main Tool: Penning Trap r B r radial confinement: = ˆ B B0 z Invariance-Relation ρ2 Φρ =2 − axial confinement: ( ,z ) Vc0 2 z 2 2 2 2 ν= ν+ + ν − + ν r c z B Vk V Modified Cyclotron Motion Axial Motion 0 Cyclotron Frequency V ν k z 1 q ν ν = ion B + c π 2 m ion Magnetron Motion ν − Φ(z ) ν = Axial z 680 kHz Magnetron ν − = 8 kHz Modified Cyclotron ν + = 28,9 MHz Proton/Antiproton Charge-to-Mass Comparison S. Ulmer et al., Nature 524 , 196 (2015) Measurements in Penning traps Cyclotron Motion Larmor Precession r g: magnetic moment in units of B nuclear magneton ω = e e c B ω = g B hω m L 2m L simple p p difficult ,-,./ 0./1./ S. Ulmer, A. Mooser et al. PRL 106, S. Ulmer, A. Mooser et al. PRL 107, 253001 (2011) 103002 (2011) ,-,. 0.1. Determinations of the q/m ratio and g-factor reduce to measurements of frequency ratios -> in principle very simple experiments –> full control, (almost) no theoretical corrections required. Frequency Measurements • Measurement of tiny image currents induced in trap electrodes -95 Low Noise Axially excited, trapped antiprotons Amp -100 -105 C R L -110 p p p Amp Amp FFT -115 -120 Signal Signal (dBm) Resonator FFT -125 -130 645300 645400 645500 645600 645700 currents: 1 fA Frequency (Hz) • In thermal equilibrium: – Particles short noise in parallel – Appear as a dip in detector spectrum – Width of the dip -> number of particles 2 1 R q ∆ν = ⋅ N 2π m D H. Nagahama et al., Rev. Sci. Instrum. 87, 113305 (2016) Measurement configuration Extract antiprotons and H - ions, compare cyclotron frequencies Park Precision Park Reservoir electrode trap electrode trap Measure , & ,J K,- antiproton H- ion 34,56 9:1;56 =12? 9:1;56 2 x 34,78 9:1;78 =12? 9:1;78 Measure ,& ,J K,- I A BC BD E5FG,78 =H 8 91 " 2 " ; Comparison of H-/antiproton cyclotron frequencies: 7 5 5 5 5 5 One frequency ratio per 4 minutes with ~ 6 ppb uncertainty Rtheo = 1.001 089 218 754 2(2) G. Gabriesle et al., PRL 82 , 3199 (1999). 12 Proton to Antiproton Q/M: Physics 9U1V;W6 "1 1 69 R 10 SZI 9U1V;W • In agreement with CPT conservation • Exceeds the energy resolution of 6521 frequency ratios previous result by a factor of 4. S. Ulmer, et al., Nature 524 , 196 (2015) • Constrain of the gravitational anomaly for antiprotons: 10 sidereal day 20 8 L-,. L-,./ I -9 39EN 1; O1P L-,. 6 - 1)/10 0 theo 4 /R Our 69 ppt result sets exp (R 2 a new upper limit of -20 (a.u.) Output Lock-In 0 ST 0 4 8 12 16 20 24 10000 100000 EN 1 Q 8.7 R 10 Time (h) Time (s) • Set limit of sidereal (diurnal) variations in • Conclusion: proton/antiproton charge-to-mass ratios Matter and Antimatter clocks run at the same frequency to < 0.72 ppb/day hω L Spin up Very very Continuous Stern hard work Gerlach Effect [./ ]./ 0./1./ , Spin down ^ [\ 2 0.1. ,- Straight- Image Current foward Measurements r B 14 Larmor Frequency – extremely hard Measurement based on continuous Stern-Gerlach effect . Energy of magnetic dipole in _` 9a. b =; magnetic field Frequency Measurement I Leading order magnetic field I d Spin is detected and analyzed via = =H " =I 9c ; correction 2 an axial frequency measurement This term adds a spin dependent quadratic axial potential -> Axial frequency becomes a function of the spin state a.=I =I Δ3e f g. .3 3 - Very difficult for the proton/antiproton system. I =Ie 0.3 i1 - Most extreme magnetic conditions ever applied to single particle. S. Ulmer, et al. PRL 106, 253001 (2011) j,e170 lc Single Penning trap method is limited to the ppm level Next Step: The Double Penning-Trap Method 0.6 0.5 0.4 0.3 0.2 0.1 spin probability flip spin 0.0 -0.1 -0.003 0.000 0.003 0.006 0.009 0.012 ν ν L/ c 0.6 0.5 0.4 0.3 0.2 0.1 0.0 spin flip probability probability flip spin -0.1 -0.002 0.000 0.002 0.004 0.006 0.008 0.010 0.012 ν /ν L c 1.) measure cyclotron , Initialize the spin state 4 2.) drive spin transition at ,mn particle transport analyze the spin state 0.4 0.4 0.4 0.4 0.2 spin up spin up 0.2 0.2 spin up 0.2 spin up (Hz) (Hz) (Hz) (Hz) z,0 z,0 z,0 z,0 ν ν ν ν 0.0 0.0 0.0 0.0 no spin-flip in PT spin flipped in PT -0.2 -0.2 -0.2 -0.2 spin down axial - frequency axial axial - frequency axial axial - frequency axial spin down spin down - frequency axial spin down -0.4 -0.4 -0.4 -0.4 0 2 4 6 8 10 12 0 2 4 6 8 10 12 0 2 4 6 8 10 12 0 2 4 6 8 10 12 measurement measurement measurement measurement measures spin flip probability as a function of the drive frequency in the homogeneous magnetic field of the precision trap The holy -grail : single antiproton spin flips C. Smorra et al., Phys. Lett. B 769, 1 (2017) • First non-destructive observation of single antiproton spin quantum transitions. The Magnetic Moment of the Antiproton 3000-fold improvement in g factor difference G. Schneider et al. , Science 358 , 1081 (2017) op ]./ ]. [\ q. rsq tur vuu wq 9tq; yH q . 2 2 2 op6 q. rsq tur vuu x 9uq; q C. Smorra et al. , Nature 550 , 371 (2017) 18 The Antiproton Magnetic Moment A milestone measurement in antimatter physics Mainz effort started BASE approved ASACUSA 1E-3 exotic atoms ATRAP ) BASE pbar +g single Penning traps p 1E-6 { > 3000 )/(g pbar -g BASE multi-Penning traps p 1E-9 { reached proton limit (BASE Mainz) 2(g principal limit of current method 1E-12 1985 1990 1995 2000 2005 2010 2015 2020 CERN COURIER, 3 / 2018. C. Smorra et al., Nature 550 , 371 (2017). year BASE achievements since 2011 Observation of spin flips with Most precise proton Precise CPT test with baryons: Most precise antiproton comparison of cyclotron frequencies a single trapped proton g-factor measurment g-factor measurment S. Ulmer, et al., Nature 524, 196 (2015) H. Nagahama, et al., Nature Comms. 8, 14084 (2017) C. Smorra et al. , Nature 550 , 371 (2017) S. Ulmer, et al., PRL 106, 253001 (2011) A. Mooser, et al., PRL 110, (2013) 9U1V; 1 " W6 1 69 R 10 SZI Application of the double 9U1V;W Penning-trap technique g/2 = 2.792 846 5 (23) g/2 = 2.792 847 350 (9) Rexp,c = 1.001 089 218 755 (64) (26) A. Mooser et al. , Nature 509 , 596 (2014). To be improved by another First direct high precision factor of 10 to 100 Sixfold improvement compared to measurement of the proton previous measurement magnetic moment.
Load more

Recommended publications
  • Interactions of Antiprotons with Atoms and Molecules
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln US Department of Energy Publications U.S. Department of Energy 1988 INTERACTIONS OF ANTIPROTONS WITH ATOMS AND MOLECULES Mitio Inokuti Argonne National Laboratory Follow this and additional works at: https://digitalcommons.unl.edu/usdoepub Part of the Bioresource and Agricultural Engineering Commons Inokuti, Mitio, "INTERACTIONS OF ANTIPROTONS WITH ATOMS AND MOLECULES" (1988). US Department of Energy Publications. 89. https://digitalcommons.unl.edu/usdoepub/89 This Article is brought to you for free and open access by the U.S. Department of Energy at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in US Department of Energy Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. /'Iud Tracks Radial. Meas., Vol. 16, No. 2/3, pp. 115-123, 1989 0735-245X/89 $3.00 + 0.00 Inl. J. Radial. Appl .. Ins/rum., Part D Pergamon Press pic printed in Great Bntam INTERACTIONS OF ANTIPROTONS WITH ATOMS AND MOLECULES* Mmo INOKUTI Argonne National Laboratory, Argonne, Illinois 60439, U.S.A. (Received 14 November 1988) Abstract-Antiproton beams of relatively low energies (below hundreds of MeV) have recently become available. The present article discusses the significance of those beams in the contexts of radiation physics and of atomic and molecular physics. Studies on individual collisions of antiprotons with atoms and molecules are valuable for a better understanding of collisions of protons or electrons, a subject with many applications. An antiproton is unique as' a stable, negative heavy particle without electronic structure, and it provides an excellent opportunity to study atomic collision theory.
    [Show full text]
  • BOTTOM, STRANGE MESONS (B = ±1, S = ∓1) 0 0 ∗ Bs = Sb, Bs = S B, Similarly for Bs ’S
    Citation: P.A. Zyla et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2020, 083C01 (2020) BOTTOM, STRANGE MESONS (B = ±1, S = ∓1) 0 0 ∗ Bs = sb, Bs = s b, similarly for Bs ’s 0 P − Bs I (J ) = 0(0 ) I , J, P need confirmation. Quantum numbers shown are quark-model predictions. Mass m 0 = 5366.88 ± 0.14 MeV Bs m 0 − mB = 87.38 ± 0.16 MeV Bs Mean life τ = (1.515 ± 0.004) × 10−12 s cτ = 454.2 µm 12 −1 ∆Γ 0 = Γ 0 − Γ 0 = (0.085 ± 0.004) × 10 s Bs BsL Bs H 0 0 Bs -Bs mixing parameters 12 −1 ∆m 0 = m 0 – m 0 = (17.749 ± 0.020) × 10 ¯h s Bs Bs H BsL = (1.1683 ± 0.0013) × 10−8 MeV xs = ∆m 0 /Γ 0 = 26.89 ± 0.07 Bs Bs χs = 0.499312 ± 0.000004 0 CP violation parameters in Bs 2 −3 Re(ǫ 0 )/(1+ ǫ 0 )=(−0.15 ± 0.70) × 10 Bs Bs 0 + − CKK (Bs → K K )=0.14 ± 0.11 0 + − SKK (Bs → K K )=0.30 ± 0.13 0 ∓ ± +0.10 rB(Bs → Ds K )=0.37−0.09 0 ± ∓ ◦ δB(Bs → Ds K ) = (358 ± 14) −2 CP Violation phase βs = (2.55 ± 1.15) × 10 rad λ (B0 → J/ψ(1S)φ)=1.012 ± 0.017 s λ = 0.999 ± 0.017 A, CP violation parameter = −0.75 ± 0.12 C, CP violation parameter = 0.19 ± 0.06 S, CP violation parameter = 0.17 ± 0.06 L ∗ 0 ACP (Bs → J/ψ K (892) ) = −0.05 ± 0.06 k ∗ 0 ACP (Bs → J/ψ K (892) )=0.17 ± 0.15 ⊥ ∗ 0 ACP (Bs → J/ψ K (892) ) = −0.05 ± 0.10 + − ACP (Bs → π K ) = 0.221 ± 0.015 0 + − ∗ 0 ACP (Bs → [K K ]D K (892) ) = −0.04 ± 0.07 HTTP://PDG.LBL.GOV Page1 Created:6/1/202008:28 Citation: P.A.
    [Show full text]
  • 1.1. Introduction the Phenomenon of Positron Annihilation Spectroscopy
    PRINCIPLES OF POSITRON ANNIHILATION Chapter-1 __________________________________________________________________________________________ 1.1. Introduction The phenomenon of positron annihilation spectroscopy (PAS) has been utilized as nuclear method to probe a variety of material properties as well as to research problems in solid state physics. The field of solid state investigation with positrons started in the early fifties, when it was recognized that information could be obtained about the properties of solids by studying the annihilation of a positron and an electron as given by Dumond et al. [1] and Bendetti and Roichings [2]. In particular, the discovery of the interaction of positrons with defects in crystal solids by Mckenize et al. [3] has given a strong impetus to a further elaboration of the PAS. Currently, PAS is amongst the best nuclear methods, and its most recent developments are documented in the proceedings of the latest positron annihilation conferences [4-8]. PAS is successfully applied for the investigation of electron characteristics and defect structures present in materials, magnetic structures of solids, plastic deformation at low and high temperature, and phase transformations in alloys, semiconductors, polymers, porous material, etc. Its applications extend from advanced problems of solid state physics and materials science to industrial use. It is also widely used in chemistry, biology, and medicine (e.g. locating tumors). As the process of measurement does not mostly influence the properties of the investigated sample, PAS is a non-destructive testing approach that allows the subsequent study of a sample by other methods. As experimental equipment for many applications, PAS is commercially produced and is relatively cheap, thus, increasingly more research laboratories are using PAS for basic research, diagnostics of machine parts working in hard conditions, and for characterization of high-tech materials.
    [Show full text]
  • ANTIMATTER a Review of Its Role in the Universe and Its Applications
    A review of its role in the ANTIMATTER universe and its applications THE DISCOVERY OF NATURE’S SYMMETRIES ntimatter plays an intrinsic role in our Aunderstanding of the subatomic world THE UNIVERSE THROUGH THE LOOKING-GLASS C.D. Anderson, Anderson, Emilio VisualSegrè Archives C.D. The beginning of the 20th century or vice versa, it absorbed or emitted saw a cascade of brilliant insights into quanta of electromagnetic radiation the nature of matter and energy. The of definite energy, giving rise to a first was Max Planck’s realisation that characteristic spectrum of bright or energy (in the form of electromagnetic dark lines at specific wavelengths. radiation i.e. light) had discrete values The Austrian physicist, Erwin – it was quantised. The second was Schrödinger laid down a more precise that energy and mass were equivalent, mathematical formulation of this as described by Einstein’s special behaviour based on wave theory and theory of relativity and his iconic probability – quantum mechanics. The first image of a positron track found in cosmic rays equation, E = mc2, where c is the The Schrödinger wave equation could speed of light in a vacuum; the theory predict the spectrum of the simplest or positron; when an electron also predicted that objects behave atom, hydrogen, which consists of met a positron, they would annihilate somewhat differently when moving a single electron orbiting a positive according to Einstein’s equation, proton. However, the spectrum generating two gamma rays in the featured additional lines that were not process. The concept of antimatter explained. In 1928, the British physicist was born.
    [Show full text]
  • Atsuko K. Ichikawa, Kyoto University
    EXPLORING PARTICLE-ANTIPARTICLE ASYMMETRY IN NEUTRINO OSCILLATION Atsuko K. Ichikawa, Kyoto University INTRODUCTION OF MYSELF • Got PhD by detecting doubly-strange nuclei using emulsion • After that, working on accelerator-based long- baseline neutrino oscillation experiments in Japan, especially on neutrino production, neutrino detector in accelerator-site and analysis. • Recently, started a high- pressure Xenon gas project for double-beta decay search 2 CONSTITUENTS OF THIS WORLD How can we distinguish btw. u, c and t Electric d, s and b charge e, and e, and Same spin, same charge… Only by mass! Except for ’s. + (Higgs, dark matter, dark energy…..?) Fig. from FNAL home page 3 HOW CAN WE DISTINGUISH NEUTRINOS? - IT IS TWO SIDES OF COINS- Neutrinos do interact with matter and 4 HOW CAN WE DISTINGUISH NEUTRINOS? - IT IS TWO SIDES OF COINS- Neutrinos do interact with matter and • An electron neutrino changes to an electron. We call this • A muon neutrino changes to a muon. categorization • A tau neutrino changes to atau. ‘flavor’. And it was believed that electron neutrino only changes to electron, never into muon nor tau before the neutrino oscillation was found. 5 NEUTRINOS DO INTERACT, BUT …. photon Concrete Wall X-ray ~1cm High Energy Mean Free path ~10cm of particles High Energy proton ~30cm ~1GeV muon ~200cm ~1GeV neutrino (atmospheric, accelerator) ~108 km≒distance btw. Solar and earth ~1MeV neutrino (solar, reactor) ~1014 km≒100 light-year 6 SUPER-KAMIOKANDE 7 SUPER-KAMIOKANDE • Since April 1996 • Water Cherenkov detector w/
    [Show full text]
  • Neutrino Masses-How to Add Them to the Standard Model
    he Oscillating Neutrino The Oscillating Neutrino of spatial coordinates) has the property of interchanging the two states eR and eL. Neutrino Masses What about the neutrino? The right-handed neutrino has never been observed, How to add them to the Standard Model and it is not known whether that particle state and the left-handed antineutrino c exist. In the Standard Model, the field ne , which would create those states, is not Stuart Raby and Richard Slansky included. Instead, the neutrino is associated with only two types of ripples (particle states) and is defined by a single field ne: n annihilates a left-handed electron neutrino n or creates a right-handed he Standard Model includes a set of particles—the quarks and leptons e eL electron antineutrino n . —and their interactions. The quarks and leptons are spin-1/2 particles, or weR fermions. They fall into three families that differ only in the masses of the T The left-handed electron neutrino has fermion number N = +1, and the right- member particles. The origin of those masses is one of the greatest unsolved handed electron antineutrino has fermion number N = 21. This description of the mysteries of particle physics. The greatest success of the Standard Model is the neutrino is not invariant under the parity operation. Parity interchanges left-handed description of the forces of nature in terms of local symmetries. The three families and right-handed particles, but we just said that, in the Standard Model, the right- of quarks and leptons transform identically under these local symmetries, and thus handed neutrino does not exist.
    [Show full text]
  • Electric Charges of Positrons and Antiprotons
    VOLUME 69, NUMBER 4 PHYSICAL REVIEW LETTERS 27 JULY 1992 Electric Charges of Positrons and Antiprotons R. J. Hughes University of California, Physics DitisionL, os Alamos IVational Laboratory, Los Alamos, IVew Mexico 87545 B. I. Deutch Institute of Physics and Astronomy, University of Aarhus, DK 8000-Aarhus C, Denmark (Received 4 May 1992) Tests of the electric charges carried by the positron and antiproton are derived from recent measure- ments of the cyclotron frequencies of these particles, and from the spectroscopy of exotic atoms in which they are constituents. PACS numbers: 14.60.Cd, 11.30.Er, 14.20.Dh, 36.10.—k There has recently been considerable interest in high- a diA'erence between the magnitudes of the charges car- precision tests of the equality of particle and antiparticle ried by protons and electrons as small as one part in 10 masses that is required by CPT symmetry [1,21. A could account for the expansion of the Universe [13]. method that has been applied to electrons and positrons This idea led to further experimental tests, and the equal- [3] and protons and antiprotons [1] utilizes the cyclotron ity of the unit of charge on the electron and the proton frequency, co q8/trt, of a particle of mass m and charge has now been tested to very high precision [14]. For in- q in a magnetic field 8. Indeed, comparisons of the cyclo- stance, Marinelli and Morpurgo quote the limit [15] tron frequencies of electrons and protons (or ions that ~ (0.8 + 0.8) x 10 'e . (2) contain these particles as constituents) in the same mag- Aq, ~ netic field are regarded as tests of the particles' mass ra- The neutron had not been discovered at the time of tios, because there is independent inforination that the Einstein's original suggestion, and Piccard and Kessler's magnitudes of the electron and proton charges are equal.
    [Show full text]
  • Dirac Equation → 4 Solutions Particle, Anti-Particle Each with Spin up +1/2, Spin Down -1/2 6 Anti-Particles: Dirac
    : CP Violation Part I Introductory concepts Slides available on my web page http://www.hep.manchester.ac.uk/u/parkes/ Chris Parkes Outline THEORETICAL CONCEPTS (with a bit of experiment) I. Introductory concepts Matter and antimatter Symmetries and conservation laws Discrete symmetries P, C and T II. CP Violation in the Standard Model Kaons and discovery of CP violation Mixing in neutral mesons Cabibbo theory and GIM mechanism The CKM matrix and the Unitarity Triangle Types of CP violation Chris Parkes 2/ Matter and antimatter Chris Parkes 4/ “Surely something is wanting in our conception of the universe... positive and negative electricity, north and south magnetism…” èMatter antimatter Symmetry “matter and antimatter may further co-exist in bodies of small mass” èParticle Antiparticle Oscillations Prof. Physics, Manchester – physics building named after Adding Relativity to QM l See Advanced QM II Free particle p2 Apply QM prescription p i = E → −! ∇ 2m 2 ! 2 ∂ψ Get Schrödinger Equation − ∇ Ψ = i! 2m dt Missing phenomena: Anti-particles, pair production, spin 2 1 2 p Or non relativistic E = mv = 2 2m Whereas relativistically E 2 −p2c2 = m2c4 Applying QM prescription again gives: 2 2 Klein-Gordon Equation 1 ∂ ψ 2 ⎛ mc ⎞ − 2 2 + ∇ ψ = ⎜ ⎟ ψ c dt ⎝ ! ⎠ Quadratic equation → 2 solutions One for particle, one for anti-particle Dirac Equation → 4 solutions particle, anti-particle each with spin up +1/2, spin down -1/2 6 Anti-particles: Dirac l Combine quantum mechanics and special relativity, linear in δt l Half of the solutions have negative predicted 1931 energy l Or positive energy anti-particles l Same mass/spin… opposite charge Chris Parkes 7 Antiparticles – Interpretation of negative energy solutions - Dirac: in terms of ‘holes’ like in semiconductors - Feynman & Stückelberg: as particles traveling backwards in time, equivalent to antiparticles traveling forward in time • both lead to the prediction of antiparticles ! Paul A.M.
    [Show full text]
  • Are Neutrinos Their Own Antiparticles?*
    Are Neutrinos Their Own Antiparticles?* Boris Kayser Fermilab, MS 106, P.O. Box 500, Batavia, IL 60510, U.S.A. Email: [email protected] Abstract: We explain the relationship between Majorana neutrinos, which are their own antiparticles, and Majorana neutrino masses. We point out that Majorana masses would make the neutrinos very distinctive particles, and explain why many theorists strongly suspect that neutrinos do have Majorana masses. The promising approach to confirming this suspicion is to seek neutrinoless double beta decay. We introduce a toy model that illustrates why this decay requires nonzero neutrino masses, even when there are both right-handed and left-handed weak currents. For given helicity h, is each neutrino mass eigenstate "i identical to its antiparticle, or different from it? Equivalently, do neutrinos have Majorana masses? If they do, then, as we shall explain, each "i is identical to its antiparticle: "i (h) = "i (h). Neutrinos of this nature are referred to as Majorana neutrinos, while ones for which "i (h) # "i!(h ) are called Dirac neutrinos. ! Let us recall what a Majorana mass is. Out of, say, a left-handed neutrino field, "L, and its charge c ! conjugate, " , one can build the “left-handed” (so called because it is constructed from " ) L ! L Majorana mass term c ! LL = mL"L"L , (1) ! ! which absorbs a (" )R and creates a "L. As this illustrates, Majorana neutrino masses mix neutrinos and antineutrinos, so they do not conserve the lepton number L that is defined by # !+ L(") = L l = #L(" ) = #L l , where l is a charged lepton.
    [Show full text]
  • ELEMENTARY PARTICLES in PHYSICS 1 Elementary Particles in Physics S
    ELEMENTARY PARTICLES IN PHYSICS 1 Elementary Particles in Physics S. Gasiorowicz and P. Langacker Elementary-particle physics deals with the fundamental constituents of mat- ter and their interactions. In the past several decades an enormous amount of experimental information has been accumulated, and many patterns and sys- tematic features have been observed. Highly successful mathematical theories of the electromagnetic, weak, and strong interactions have been devised and tested. These theories, which are collectively known as the standard model, are almost certainly the correct description of Nature, to first approximation, down to a distance scale 1/1000th the size of the atomic nucleus. There are also spec- ulative but encouraging developments in the attempt to unify these interactions into a simple underlying framework, and even to incorporate quantum gravity in a parameter-free “theory of everything.” In this article we shall attempt to highlight the ways in which information has been organized, and to sketch the outlines of the standard model and its possible extensions. Classification of Particles The particles that have been identified in high-energy experiments fall into dis- tinct classes. There are the leptons (see Electron, Leptons, Neutrino, Muonium), 1 all of which have spin 2 . They may be charged or neutral. The charged lep- tons have electromagnetic as well as weak interactions; the neutral ones only interact weakly. There are three well-defined lepton pairs, the electron (e−) and − the electron neutrino (νe), the muon (µ ) and the muon neutrino (νµ), and the (much heavier) charged lepton, the tau (τ), and its tau neutrino (ντ ). These particles all have antiparticles, in accordance with the predictions of relativistic quantum mechanics (see CPT Theorem).
    [Show full text]
  • Field Theory and the Standard Model
    Field theory and the Standard Model W. Buchmüller and C. Lüdeling Deutsches Elektronen-Synchrotron DESY, 22607 Hamburg, Germany Abstract We give a short introduction to the Standard Model and the underlying con- cepts of quantum field theory. 1 Introduction In these lectures we shall give a short introduction to the Standard Model of particle physics with empha- sis on the electroweak theory and the Higgs sector, and we shall also attempt to explain the underlying concepts of quantum field theory. The Standard Model of particle physics has the following key features: – As a theory of elementary particles, it incorporates relativity and quantum mechanics, and therefore it is based on quantum field theory. – Its predictive power rests on the regularization of divergent quantum corrections and the renormal- ization procedure which introduces scale-dependent `running couplings'. – Electromagnetic, weak, strong and also gravitational interactions are all related to local symmetries and described by Abelian and non-Abelian gauge theories. – The masses of all particles are generated by two mechanisms: confinement and spontaneous sym- metry breaking. In the following chapters we shall explain these points one by one. Finally, instead of a summary, we briefly recall the history of `The making of the Standard Model' [1]. From the theoretical perspective, the Standard Model has a simple and elegant structure: it is a chiral gauge theory. Spelling out the details reveals a rich phenomenology which can account for strong and electroweak interactions, confinement and spontaneous symmetry breaking, hadronic and leptonic flavour physics etc. [2, 3]. The study of all these aspects has kept theorists and experimenters busy for three decades.
    [Show full text]
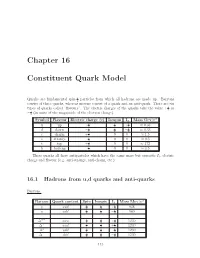
  • Chapter 16 Constituent Quark Model
    Chapter 16 Constituent Quark Model 1 Quarks are fundamental spin- 2 particles from which all hadrons are made up. Baryons consist of three quarks, whereas mesons consist of a quark and an anti-quark. There are six 2 types of quarks called “flavours”. The electric charges of the quarks take the value + 3 or 1 (in units of the magnitude of the electron charge). − 3 2 Symbol Flavour Electric charge (e) Isospin I3 Mass Gev /c 2 1 1 u up + 3 2 + 2 0.33 1 1 1 ≈ d down 3 2 2 0.33 − 2 − ≈ c charm + 3 0 0 1.5 1 ≈ s strange 3 0 0 0.5 − 2 ≈ t top + 3 0 0 172 1 ≈ b bottom 0 0 4.5 − 3 ≈ These quarks all have antiparticles which have the same mass but opposite I3, electric charge and flavour (e.g. anti-strange, anti-charm, etc.) 16.1 Hadrons from u,d quarks and anti-quarks Baryons: 2 Baryon Quark content Spin Isospin I3 Mass Mev /c 1 1 1 p uud 2 2 + 2 938 n udd 1 1 1 940 2 2 − 2 ++ 3 3 3 ∆ uuu 2 2 + 2 1230 + 3 3 1 ∆ uud 2 2 + 2 1230 0 3 3 1 ∆ udd 2 2 2 1230 3 3 − 3 ∆− ddd 1230 2 2 − 2 113 1 1 3 Three spin- 2 quarks can give a total spin of either 2 or 2 and these are the spins of the • baryons (for these ‘low-mass’ particles the orbital angular momentum of the quarks is zero - excited states of quarks with non-zero orbital angular momenta are also possible and in these cases the determination of the spins of the baryons is more complicated).
    [Show full text]