Step-Gap “E” Core Swing Chokes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Class-E Audio Modulated Tesla Coil Instruction Manual
Class-E Audio Modulated Tesla Coil CCllaassss--EE AAuuddiioo MMoodduullaatteedd TTeessllaa CCooiill IInnssttrruuccttiioonn MMaannuuaall Eastern Voltage Research, LLC May 19, 2017 REV F − 1 − http://www.EasternVoltageResearch.com Class-E Tesla Coil Instruction Manual Class-E Audio Modulated Tesla Coil BOARD REVISION C This manual only applies to the new Revision C PCB boards. These boards can be identified by their red or green silkscreen color as well as the marking SC2076 REV C which is located underneath the location for T41 on the upper right of the PCB board. May 19, 2017 REV F − 2 − http://www.EasternVoltageResearch.com Class-E Tesla Coil Instruction Manual Class-E Audio Modulated Tesla Coil AGE DISCLAIMER THIS KIT IS AN ADVANCED, HIGH POWER SOLID STATE POWER DEVICE. IT IS INTENDED FOR USE FOR INDIVIDUALS OVER 18 YEARS OF AGE WITH THE PROPER KNOWLEDGE AND EXPERIENCE, AS WELL AS FAMILIARITY WITH LINE VOLTAGE POWER CIRCUITS. BY BUILDING, USING, OR OPERATING THIS KIT, YOU ACKNOWLEDGE THAT YOU ARE OVER 18 YEARS OF AGE, AND THAT YOU HAVE THOROUGHLY READ THROUGH THE SAFETY INFORMATION PRESENTED IN THIS MANUAL. THIS KIT SHALL NOT BE USED AT ANY TIME BY INDIVIDUALS UNDER 18 YEARS OF AGE. May 19, 2017 REV F − 3 − http://www.EasternVoltageResearch.com Class-E Tesla Coil Instruction Manual Class-E Audio Modulated Tesla Coil SAFETY AND EQUIPMENT HAZARDS PLEASE BE SURE TO READ AND UNDERSTAND ALL SAFETY AND EQUIPMENT RELATED HAZARDS AND WARNINGS BEFORE BUILDING AND OPERATING YOUR KIT. THE PURPOSE OF THESE WARNINGS IS NOT TO SCARE YOU, BUT TO KEEP YOU WELL INFORMED TO WHAT HAZARDS MAY APPLY FOR YOUR PARTICULAR KIT. -

Common Mode Chokes by Würth Elektronik
Welcome! Inductors & EMC-Ferrites Basics - Parts and Applications Wurth Electronics Inc. Field Application Engineer Michael Eckert Würth Elektronik eiSos © May/2006 Michael Eckert What is an Inductor ? technical view: a piece of wire wounded on something a filter an energy-storage-part (short-time) examples: Würth Elektronik eiSos © May/2006 Michael Eckert What is an EMC-Ferrite ? Technical view: Frequency dependent filter Absorber for RF-energy examples: EMC Snap-Ferrites EMC-Ferrites for SMD-Ferrites Flatwire Würth Elektronik eiSos © May/2006 Michael Eckert Magnetic Field Strenght H of some configurations I long, straight wire H = 2⋅π ⋅R N⋅I Toroidal Coil H = 2⋅π ⋅R N⋅I Long solenoid H = l (e.g. rod core indcutor) Würth Elektronik eiSos © May/2006 Michael Eckert Example: Conducted Emission Measurement • Dosing pump for chemicals industry. Würth Elektronik eiSos © May/2006 Michael Eckert Conducted Emission Measurement • Power supply V 1.0 PCB Buck Converter ST L4960/2.5A/fs 85-115KHz Würth Elektronik eiSos © May/2006 Michael Eckert Conducted Emission Measurement • Power supply V 1.1 PCB Schematic Würth Elektronik eiSos © May/2006 Michael Eckert Awareness: • Select the right parts for your application • Do not always look on cost Very easy solution with a dramatic result!!! or Choke before Choke after Würth Elektronik eiSos © May/2006 Michael Eckert What is permeability [ur]? – Permability (µr): describe the capacity of concentration of the magnetic flux in the material. typical permeabilities [µr] : Magnetic induction in ferrite: -

Custom Power Supplies, Transformers, Chokes & Reactors
YOUR POWER SOURCE Custom Power Supplies, Transformers, Chokes & Reactors NeeltranThe Story Transformers and Power Supplies • Industry Leader since 1973 Neeltran has become the most reliable supplier of Transformers and Power Supply Systems in the industry. Our engineers, along with our manufacturing team, have the knowledge and ability to meet the special needs of our customers. All power supplies are custom designed to your specifications by our engineering staff and completely fabricated in-house at our manufacturing facility. Our facilities and experience include: • Research & Development Since 1973 Neeltran has been a leading • Test Laboratory manufacturer of transformers and • Design Engineering power supplies. • Printed Circuit Board Manufacturing Our general product range is: • Steel Cutting Machinery • Dry Type and Water Cooled Transformers: • Baking Ovens 5–10,000 KVA (up to 25 KV input) • Vacuum Pressure Impregnation Tanks (Outputs up to 300 KV and 50 KHZ) • Coil Winding Equipment • Oil filled Transformers (Rectifier type only): 100 KVA to 50 MVA (up to 69 KV input) • Painting and Steel Fabrication to manufacture our own enclosures • Oil filled high frequency Transformers: • Assembly Areas up to 50 KHZ, 2000 KVA, up to 50 KV output Industry standards are maintained with our • Cast Coil Transformers: up to 20 MVA testing equipment assuring that all shipped (up to 35 KV input) products meet customer’s requirements and • Chokes and Reactors air or iron: specifications. Impulse testing as well as customer up to 25 KV, 20,000 amps specific testing is available upon request. • Power Supplies: 100 A to 500,000 amp (AC or DC) 1500 VDC. Special outputs up to 300,000 volts AC or DC and high frequencies are available. -

Checking out the Power Supply the Power Supply Must Be Carefully Checked out a Good Many Australian-Made Sets from the Mid 1930S-1950 Era
Checking out the power supply The power supply must be carefully checked out a good many Australian-made sets from the mid 1930s-1950 era. Fig.1 before switching on a vintage radio. The shows a typical circuit configura- components most likely to be at fault are the tion but there are other variations. electrolytic capacitors, most of which should be For example, some rectifiers re- quire a cathode voltage of 6.3V AC, replaced as a matter of course. not 5V. Similarly, not all radio valves use Although only a few parts are in- (equivalent to 570 volts, centre- 6.3V heater supplies. There are volved, the power supply is a com- tapped). 2.5V valves, 4V valves and 12V mon source of problems in vintage The 5V and 6.3V AC supplies are valves in some late model sets. In radios. It should be carefully check- wired straight from the trans- these radios, the low tension ed out before power is applied, as a former to the filaments and voltages on the transformer will be fault here can quickly cause heaters. However, the high tension different — but that's about all. damage to critical components. supply must be rectified to give a The high tension voltage will still be Most mains-operated valve high-tension DC supply for the well in excess of 250 volts. radios have three separate secon- anodes and screens for the various The output from the rectifier dary windings on the power receiving and output valves. A valve will not be pure DC but does transformer. -

Designing Magnetic Components for Optimum Performance Article
Power Supply Design Seminar Designing Magnetic Components for Optimum Performance in Low-Cost AC/DC Converter Applications Topic Category: Magnetic Component Design Reproduced from 2010 Texas Instruments Power Supply Design Seminar SEM1900, Topic 5 TI Literature Number: SLUP265 © 2010, 2011 Texas Instruments Incorporated Power Seminar topics and online power- training modules are available at: power.ti.com/seminars Designing Magnetic Components for Optimum Performance in Low-Cost AC/DC Converter Applications Seamus O’Driscoll, Peter Meaney, John Flannery, and George Young AbstrAct Assuming that the reader is familiar with basic magnetic design theory, this topic provides design guidance to achieve high efficiency, low electromagnetic interference (EMI), and manufacturing ease for the magnetic components in typical offline power converters. Magnetic-component designs for a 90-W notebook adapter and a 300-W ATX power supply are used as examples. Magnetic applications to be considered include the input EMI filter, power inductor design, high-voltage (HV) level-shifting gate drives, and single- and multiple-output forward-mode transformers in both wound and planar formats. The techniques are also applied to flyback “transformers” (coupled inductors) and will enable lower- profile designs with lower intrinsic common-mode noise generation. I. IntroductIon Gate Drive Note: The SI (extended MKS) units system AC Filter PFC Isolated Main Drive (for some Converter Output(s) is used throughout this topic. CM Inductor, topologies), Balanced Bridge, Differential This material is intended as a high- PFC Inductor, Multi-Output Filter level overview of the primary consider- Bias Flyback ations when designing magnetic components for high-volume and cost- Isolated Feedback optimized applications such as computer Fig. -

Measured Data for Chokes Wound on New Big #31 Toroid
A New Choke Cookbook for the 160–10M Bands Using Fair-Rite #31 2.4-in o.d. (2631803802) and 4-in o.d. (2631814002) Toroids © 2018-19 by James W. Brown All Rights Reserved Introduction: Common mode chokes are added as series elements to a transmission line to kill common mode current. The line may be a short one carrying audio or control signals between a computer and a radio, video between a computer and a monitor, noisy power wiring, or feedlines for antennas. This application note focuses on the use of chokes on the feedlines of high power transmitting antennas to suppress received noise, to minimize RF in the shack (and a neighbor’s living room) and to minimize crosstalk between stations in multi-transmitter environments. Fundamentals Differential mode current is the normal transmission of power or other signals inside coax, or between paired conductors. The currents in the two conductors are precisely equal and are out of polarity (that is, flowing in opposite directions at each point along the line). Because the current in the two conductors are equal and out of polarity, they do not radiate, nor do they receive. Common mode current is carried on the outside of the coax shield, or as the difference of unequal currents on the two conductors of 2-wire line. A line carrying common mode current acts as antenna for both transmit and receive. Common mode current that couples to the antenna changes the directional pattern of an antenna by filling in the nulls of it’s directional pattern. -

Ferrite EMI Cable Cores Electro-Magnetic Interference Solutions
global solutions : local support ™ Ferrite EMI Cable Cores Electro-Magnetic Interference Solutions www.lairdtech.com Laird Technologies is the world leader in the design and supply of customized performance critical products for wireless and other advanced electronic applications. Laird Technologies partners with it's customers to help find solutions for applications in various industries such as: Aerospace Automotive Electronics Computers Consumer Electronics Data Communications Medical Equipment Military Network Equipment Telecommunications Laird Technologies offers its customers unique product solutions, dedication to research and development and a seamless network of manufacturing and customer support facilities located all across the globe. global solutions : local support ™ www.lairdtech.com Contents Ferrite Material Impedance Comparison ................................. 4 Design & Selection “Rules of Thumb” ..................................... 4 High Frequency (HFB-) Cylindrical Cores .................................. 5 High Frequency (HFA-) Split, Snap-On Cores ........................... 6 Broadband (28B-) Cylindrical Cores ........................................ 7 Broadband (28A-) Split, Snap-On Cores ................................ 10 Sorted Quick Reference Charts Broadband (28B- and 28A-) Cable Cores .......................... 12 Low Frequency (LFB-) Cylinderical Cores ............................... 14 Broadband (28R-) Ribbon & Flex Cable Cores ....................... 15 Broadband (28S-) Split Ribbion & Flex Cable Cores -

Ring Core Chokes with Iron Powder Core
Inductors Power line chokes Ring core chokes with iron powder core Date: October 2008 Data Sheet EPCOS AG 2008. Reproduction, publication and dissemination of this publication, enclosures hereto and the information contained therein without EPCOS’ prior express consent is prohibited. Power line chokes Ring core chokes with iron powder core General Magnetic flux induced in core by Operating current operating current Core Windings Source of Line through which interference current flows Magnetic flux Differential-mode interference induced in core by current, symmetrical interference current interference IND0825-B-E Figure 1 Ring core choke with powder core Double choke shown as an example Ring core chokes with iron powder core are primarily used to attenuate differential-mode interference voltages and currents in cases where the use of X capacitors is ineffective, inadequate or undesired. In order to avoid saturation, these chokes are equipped with a closed ring core of iron powder with low permeability. They are often installed together with current-compensated chokes to improve differential-mode interference attenuation, especially at low frequencies. Single chokes with powder core attenuate differential-mode RF interference on the connected line. Both windings of double chokes act as if they were connected in series, their effect on differential- mode interference corresponds, in practice, to roughly 3.5 times their rated inductance. Common-mode interference is also attenuated by double chokes with powder core; maximally half the rated inductance of one winding is effective. As with I core chokes – the rated inductance is only minimally affected by operating current bias. Due to the closed core, the stray field, however, is substantially lower than that of a corresponding I core choke. -
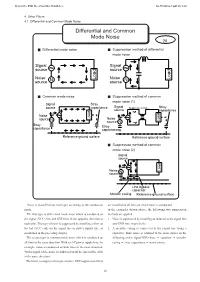
Differential and Common Mode Noise Differential and Common Mode Noise 26
This is the PDF file of text No.TE04EA-1. No.TE04EA-1.pdf 98.3.20 4. Other Filters 4.1. Differential and Common Mode Noise Differential and Common Mode Noise 26 ■ Differential mode noise ■ Suppression method of differential mode noise Signal Signal source source Load Noise Noise Load source N source N ■ Common mode noise ■ Suppression method of common mode noise (1) Signal Stray source capacitance Signal Suppresses noise. Stray source capacitance Noise source Load Noise N source N Load Stray Stray capacitance capacitance Reference ground surface Reference ground surface ■ Suppression method of common mode noise (2) Signal source Noise Load source N Line bypass capacitor Metallic casing Reference ground surface Noise is classified into two types according to the conduction are installed on all lines on which[Notes] noise is conducted. mode. In the examples shown above, the following two suppression The first type is differential mode noise which is conducted on methods are applied. the signal (VCC) line and GND line in the opposite direction to 1. Noise is suppressed by installing an inductor to the signal line each othe. This type of noise is suppressed by installing a filter on and GND line, respectively. the hot (VCC) side on the signal line or power supply line, as 2. A metallic casing is connected to the signal line using a mentioned in the preceding chapter. capacitor. Thus, noise is returned to the noise source in the The second type is common mode noise which is conducted on following order; signal/GND lines ➝ capacitor ➝ metallic all lines in the same direction. -

Performance Comparison of Phase Change Materials and Metal-Insulator Transition Materials for Direct Current and Radio Frequency Switching Applications
technologies Review Performance Comparison of Phase Change Materials and Metal-Insulator Transition Materials for Direct Current and Radio Frequency Switching Applications Protap Mahanta, Mohiuddin Munna and Ronald A. Coutu Jr. * Department of Electrical and Computer Engineering, Marquette University, Milwaukee, WI 53233, USA; [email protected] (P.M.); [email protected] (M.M.) * Correspondence: [email protected]; Tel.: +1-414-288-7316 Received: 29 March 2018; Accepted: 1 May 2018; Published: 4 May 2018 Abstract: Advanced understanding of the physics makes phase change materials (PCM) and metal-insulator transition (MIT) materials great candidates for direct current (DC) and radio frequency (RF) switching applications. In the literature, germanium telluride (GeTe), a PCM, and vanadium dioxide (VO2), an MIT material have been widely investigated for DC and RF switching applications due to their remarkable contrast in their OFF/ON state resistivity values. In this review, innovations in design, fabrication, and characterization associated with these PCM and MIT material-based RF switches, have been highlighted and critically reviewed from the early stage to the most recent works. We initially report on the growth of PCM and MIT materials and then discuss their DC characteristics. Afterwards, novel design approaches and notable fabrication processes; utilized to improve switching performance; are discussed and reviewed. Finally, a brief vis-á-vis comparison of resistivity, insertion loss, isolation loss, power consumption, RF power handling capability, switching speed, and reliability is provided to compare their performance to radio frequency microelectromechanical systems (RF MEMS) switches; which helps to demonstrate the current state-of-the-art, as well as insight into their potential in future applications. -

Winding Resistance and Winding Power Loss of High-Frequency Power Inductors
Wright State University CORE Scholar Browse all Theses and Dissertations Theses and Dissertations 2012 Winding Resistance and Winding Power Loss of High-Frequency Power Inductors Rafal P. Wojda Wright State University Follow this and additional works at: https://corescholar.libraries.wright.edu/etd_all Part of the Computer Engineering Commons, and the Computer Sciences Commons Repository Citation Wojda, Rafal P., "Winding Resistance and Winding Power Loss of High-Frequency Power Inductors" (2012). Browse all Theses and Dissertations. 1095. https://corescholar.libraries.wright.edu/etd_all/1095 This Dissertation is brought to you for free and open access by the Theses and Dissertations at CORE Scholar. It has been accepted for inclusion in Browse all Theses and Dissertations by an authorized administrator of CORE Scholar. For more information, please contact [email protected]. WINDING RESISTANCE AND WINDING POWER LOSS OF HIGH-FREQUENCY POWER INDUCTORS A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy By Rafal Piotr Wojda B. Tech., Warsaw University of Technology, Warsaw, Poland, 2007 M. S., Warsaw University of Technology, Warsaw, Poland, 2009 2012 Wright State University WRIGHT STATE UNIVERSITY GRADUATE SCHOOL August 20, 2012 I HEREBY RECOMMEND THAT THE DISSERTATION PREPARED UNDER MY SUPERVISION BY Rafal Piotr Wojda ENTITLED Winding Resistance and Winding Power Loss of High-Frequency Power Inductors BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Doctor of Philosophy. Marian K. Kazimierczuk, Ph.D. Dissertation Director Ramana V. Grandhi, Ph.D. Director, Ph.D. in Engineering Program Andrew Hsu, Ph.D. Dean, Graduate School Committee on Final Examination Marian K. -

Common Mode Chokes Serge Stroobandt, ON4AA
Common Mode Chokes Serge Stroobandt, ON4AA Copyright 2013–2020, licensed under Creative Commons BY-NC-SA Definitions Differential mode The differential mode is the normal mode of a transmission line (both coax and twin line alike) where the currents flow in opposite directions in its con- ductors. In differential mode, a transmission line behaves as two conductors. The currents are opposite on the inside of a coaxial cable and there is no current flowing on the outside. Common mode The common mode of a transmission line is where the currents flow in the same direction in its conductors. In common mode, a transmission line be- haves as a single conductor. The currents flow in the same direction on the in- side of a coaxial cable and there is also a current flowing on the outside. The common mode along the feed line is actually a surface wave, which field diminishes exponentially in the radial direction. The phase velocity of a surface wave can, depending on the involved dielectric interfaces, be slower than the speed of light, equal in speed or even faster than the speed of light! Fore sure, the group (energy) velocity can never be faster than the speed of light. I grew up in Ostend, at the North Sea coast; so I love to make com- parisons with visible sea wave phenomena: When a sea wave crest with a certain velocity hits a dyke (shore wall) at an angle, the point of intersec- tion between the wave crest and the dyke will travel along the dyke at a ve- locity superior to the original sea wave velocity.