Measuring Mean Densities of Δ Scuti Stars with Asteroseismology Theoretical Properties of Large Separations Using TOUCAN
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Variable Star Classification and Light Curves Manual
Variable Star Classification and Light Curves An AAVSO course for the Carolyn Hurless Online Institute for Continuing Education in Astronomy (CHOICE) This is copyrighted material meant only for official enrollees in this online course. Do not share this document with others. Please do not quote from it without prior permission from the AAVSO. Table of Contents Course Description and Requirements for Completion Chapter One- 1. Introduction . What are variable stars? . The first known variable stars 2. Variable Star Names . Constellation names . Greek letters (Bayer letters) . GCVS naming scheme . Other naming conventions . Naming variable star types 3. The Main Types of variability Extrinsic . Eclipsing . Rotating . Microlensing Intrinsic . Pulsating . Eruptive . Cataclysmic . X-Ray 4. The Variability Tree Chapter Two- 1. Rotating Variables . The Sun . BY Dra stars . RS CVn stars . Rotating ellipsoidal variables 2. Eclipsing Variables . EA . EB . EW . EP . Roche Lobes 1 Chapter Three- 1. Pulsating Variables . Classical Cepheids . Type II Cepheids . RV Tau stars . Delta Sct stars . RR Lyr stars . Miras . Semi-regular stars 2. Eruptive Variables . Young Stellar Objects . T Tau stars . FUOrs . EXOrs . UXOrs . UV Cet stars . Gamma Cas stars . S Dor stars . R CrB stars Chapter Four- 1. Cataclysmic Variables . Dwarf Novae . Novae . Recurrent Novae . Magnetic CVs . Symbiotic Variables . Supernovae 2. Other Variables . Gamma-Ray Bursters . Active Galactic Nuclei 2 Course Description and Requirements for Completion This course is an overview of the types of variable stars most commonly observed by AAVSO observers. We discuss the physical processes behind what makes each type variable and how this is demonstrated in their light curves. Variable star names and nomenclature are placed in a historical context to aid in understanding today’s classification scheme. -
![Arxiv:2006.10868V2 [Astro-Ph.SR] 9 Apr 2021 Spain and Institut D’Estudis Espacials De Catalunya (IEEC), C/Gran Capit`A2-4, E-08034 2 Serenelli, Weiss, Aerts Et Al](https://docslib.b-cdn.net/cover/3592/arxiv-2006-10868v2-astro-ph-sr-9-apr-2021-spain-and-institut-d-estudis-espacials-de-catalunya-ieec-c-gran-capit-a2-4-e-08034-2-serenelli-weiss-aerts-et-al-1213592.webp)
Arxiv:2006.10868V2 [Astro-Ph.SR] 9 Apr 2021 Spain and Institut D’Estudis Espacials De Catalunya (IEEC), C/Gran Capit`A2-4, E-08034 2 Serenelli, Weiss, Aerts Et Al
Noname manuscript No. (will be inserted by the editor) Weighing stars from birth to death: mass determination methods across the HRD Aldo Serenelli · Achim Weiss · Conny Aerts · George C. Angelou · David Baroch · Nate Bastian · Paul G. Beck · Maria Bergemann · Joachim M. Bestenlehner · Ian Czekala · Nancy Elias-Rosa · Ana Escorza · Vincent Van Eylen · Diane K. Feuillet · Davide Gandolfi · Mark Gieles · L´eoGirardi · Yveline Lebreton · Nicolas Lodieu · Marie Martig · Marcelo M. Miller Bertolami · Joey S.G. Mombarg · Juan Carlos Morales · Andr´esMoya · Benard Nsamba · KreˇsimirPavlovski · May G. Pedersen · Ignasi Ribas · Fabian R.N. Schneider · Victor Silva Aguirre · Keivan G. Stassun · Eline Tolstoy · Pier-Emmanuel Tremblay · Konstanze Zwintz Received: date / Accepted: date A. Serenelli Institute of Space Sciences (ICE, CSIC), Carrer de Can Magrans S/N, Bellaterra, E- 08193, Spain and Institut d'Estudis Espacials de Catalunya (IEEC), Carrer Gran Capita 2, Barcelona, E-08034, Spain E-mail: [email protected] A. Weiss Max Planck Institute for Astrophysics, Karl Schwarzschild Str. 1, Garching bei M¨unchen, D-85741, Germany C. Aerts Institute of Astronomy, Department of Physics & Astronomy, KU Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium and Department of Astrophysics, IMAPP, Radboud University Nijmegen, Heyendaalseweg 135, 6525 AJ Nijmegen, the Netherlands G.C. Angelou Max Planck Institute for Astrophysics, Karl Schwarzschild Str. 1, Garching bei M¨unchen, D-85741, Germany D. Baroch J. C. Morales I. Ribas Institute of· Space Sciences· (ICE, CSIC), Carrer de Can Magrans S/N, Bellaterra, E-08193, arXiv:2006.10868v2 [astro-ph.SR] 9 Apr 2021 Spain and Institut d'Estudis Espacials de Catalunya (IEEC), C/Gran Capit`a2-4, E-08034 2 Serenelli, Weiss, Aerts et al. -
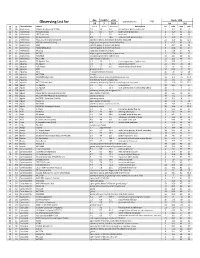
Observing List
day month year Epoch 2000 local clock time: 2.00 Observing List for 24 7 2019 RA DEC alt az Constellation object mag A mag B Separation description hr min deg min 39 64 Andromeda Gamma Andromedae (*266) 2.3 5.5 9.8 yellow & blue green double star 2 3.9 42 19 51 85 Andromeda Pi Andromedae 4.4 8.6 35.9 bright white & faint blue 0 36.9 33 43 51 66 Andromeda STF 79 (Struve) 6 7 7.8 bluish pair 1 0.1 44 42 36 67 Andromeda 59 Andromedae 6.5 7 16.6 neat pair, both greenish blue 2 10.9 39 2 67 77 Andromeda NGC 7662 (The Blue Snowball) planetary nebula, fairly bright & slightly elongated 23 25.9 42 32.1 53 73 Andromeda M31 (Andromeda Galaxy) large sprial arm galaxy like the Milky Way 0 42.7 41 16 53 74 Andromeda M32 satellite galaxy of Andromeda Galaxy 0 42.7 40 52 53 72 Andromeda M110 (NGC205) satellite galaxy of Andromeda Galaxy 0 40.4 41 41 38 70 Andromeda NGC752 large open cluster of 60 stars 1 57.8 37 41 36 62 Andromeda NGC891 edge on galaxy, needle-like in appearance 2 22.6 42 21 67 81 Andromeda NGC7640 elongated galaxy with mottled halo 23 22.1 40 51 66 60 Andromeda NGC7686 open cluster of 20 stars 23 30.2 49 8 46 155 Aquarius 55 Aquarii, Zeta 4.3 4.5 2.1 close, elegant pair of yellow stars 22 28.8 0 -1 29 147 Aquarius 94 Aquarii 5.3 7.3 12.7 pale rose & emerald 23 19.1 -13 28 21 143 Aquarius 107 Aquarii 5.7 6.7 6.6 yellow-white & bluish-white 23 46 -18 41 36 188 Aquarius M72 globular cluster 20 53.5 -12 32 36 187 Aquarius M73 Y-shaped asterism of 4 stars 20 59 -12 38 33 145 Aquarius NGC7606 Galaxy 23 19.1 -8 29 37 185 Aquarius NGC7009 -

The VVV Templates Project Towards an Automated Classification of VVV
A&A 567, A100 (2014) Astronomy DOI: 10.1051/0004-6361/201423904 & c ESO 2014 Astrophysics The VVV Templates Project Towards an automated classification of VVV light-curves I. Building a database of stellar variability in the near-infrared R. Angeloni1,2,3, R. Contreras Ramos1,4, M. Catelan1,2,4,I.Dékány4,1,F.Gran1,4, J. Alonso-García1,4,M.Hempel1,4, C. Navarrete1,4,H.Andrews1,6, A. Aparicio7,21,J.C.Beamín1,4,8,C.Berger5, J. Borissova9,4, C. Contreras Peña10, A. Cunial11,12, R. de Grijs13,14, N. Espinoza1,15,4, S. Eyheramendy15,4, C. E. Ferreira Lopes16, M. Fiaschi12, G. Hajdu1,4,J.Han17,K.G.Hełminiak18,19,A.Hempel20,S.L.Hidalgo7,21,Y.Ita22, Y.-B. Jeon23, A. Jordán1,2,4, J. Kwon24,J.T.Lee17, E. L. Martín25,N.Masetti26, N. Matsunaga27,A.P.Milone28,D.Minniti4,20,L.Morelli11,12, F. Murgas7,21, T. Nagayama29,C.Navarro9,4,P.Ochner12,P.Pérez30, K. Pichara5,4, A. Rojas-Arriagada31, J. Roquette32,R.K.Saito33, A. Siviero12, J. Sohn17, H.-I. Sung23,M.Tamura27,24,R.Tata7,L.Tomasella12, B. Townsend1,4, and P. Whitelock34,35 (Affiliations can be found after the references) Received 29 March 2014 / Accepted 13 May 2014 ABSTRACT Context. The Vista Variables in the Vía Láctea (VVV) ESO Public Survey is a variability survey of the Milky Way bulge and an adjacent section of the disk carried out from 2010 on ESO Visible and Infrared Survey Telescope for Astronomy (VISTA). The VVV survey will eventually deliver a deep near-IR atlas with photometry and positions in five passbands (ZYJHKS) and a catalogue of 1−10 million variable point sources – mostly unknown – that require classifications. -

Pulsating Variable Stars and the Hertzsprung-Russell Diagram
- !% ! $1!%" % Studying intrinsically pulsating variable stars plays a very important role in stellar evolution under- standing. The Hertzsprung-Russell diagram is a powerful tool to track which stage of stellar life is represented by a particular type of variable stars. Let's see what major pulsating variable star types are and learn about their place on the H-R diagram. This approach is very useful, as it also allows to make a decision about a variability type of a star for which the properties are known partially. The Hertzsprung-Russell diagram shows a group of stars in different stages of their evolution. It is a plot showing a relationship between luminosity (or abso- lute magnitude) and stars' surface temperature (or spectral type). The bottom scale is ranging from high-temperature blue-white stars (left side of the diagram) to low-temperature red stars (right side). The position of a star on the diagram provides information about its present stage and its mass. Stars that burn hydrogen into helium lie on the diagonal branch, the so-called main sequence. In this article intrinsically pulsating variables are covered, showing their place on the H-R diagram. Pulsating variable stars form a broad and diverse class of objects showing the changes in brightness over a wide range of periods and magnitudes. Pulsations are generally split into two types: radial and non-radial. Radial pulsations mean the entire star expands and shrinks as a whole, while non- radial ones correspond to expanding of one part of a star and shrinking the other. Since the H-R diagram represents the color-luminosity relation, it is fairly easy to identify not only the effective temperature Intrinsic variable types on the Hertzsprung–Russell and absolute magnitude of stars, but the evolutionary diagram. -

THE EUROWET CO-OPERATION J.-E. Solheim
Baltic Astronomy, vol. 7, 319-328, 1998. THE EUROWET CO-OPERATION J.-E. Solheim Department of Physics, University of Troms0, N-9037 Troms0, Norway Received March 1, 1998. Abstract. The WET groups in Europe co-operate on many levels. With a grant from the European Union, instrument development, joint observing campaigns and some short-time support for young scientists have been possible. At the moment the grant has expired, but instrument development continues with own funds, concentrating on the development of high-speed CCD photometers. Key words: observing campaigns - observing networks - instru- mentation: CCD photometers 1. INTRODUCTION The aim of WET is to engage astronomers from all continents in joint observing campaigns and to develop instruments and cre- ate tools for analysing the data acquired. In principle, any sub- organizations should not be necessary. Our slogan is that the Whole Earth is our telescope, and we should work ideally as one unit. How- ever, in order to apply for funding related to the geographically lim- ited area, we found it necessary to organise the European partners in WET. The result of this will be explained in the following. WET has not always been a world-wide co-operation. We must remember that the original idea behind WET was that it should be an instrument for Texas astronomers to observe their targets. Colleagues around the world should apply for observing time, and observers from Texas should bring their instruments, do the obser- vations and bring the data home for analysis. This did not work. It soon became obvious that it would be too expensive to travel all over the world from Texas for each campaign. -
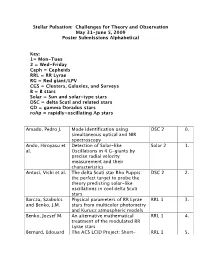
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical Key: 1= Mon-Tues 2 = Wed-Friday Ceph = Cepheids RRL = RR Lyrae RG = Red giant/LPV CGS = Clusters, Galaxies, and Surveys B = B stars Solar = Sun and solar-type stars DSC = delta Scuti and related stars GD = gamma Doradus stars roAp = rapidly-oscillating Ap stars Amado, Pedro J. Mode identification using DSC 2 0. simultaneous optical and NIR spectroscopy Ando, Hiroyasu et Detection of Solar-like Solar 2 1. al. Oscillations in 4 G-giants by precise radial velocity measurement and their characteristics Antoci, Vichi et al. The delta Scuti star Rho Puppis: DSC 2 2. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Barcza, Szabolcs Physical parameters of RR Lyrae RRL 1 3. and Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical RRL 1 4. treatment of the modulated RR Lyrae stars Bernard, Edouard The ACS LCID Project: Short- RRL 1 5. for the LCID Team period variables Bersier, David et A large-scale survey for variable CGS 1 6. al. stars in M33 Bouabid, Mehdi- Frequency analysis of the SISMO GD 2 7. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid GD 2 8. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Cameron, Chris et Asteroseismic tuning of the roAp 2 9. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the B 2 10. al. MOST asteroseismic potential Cameron, Chris, Frequency Analysis of the Beta B 2 11. -

Astrophysics
Publications of the Astronomical Institute rais-mf—ii«o of the Czechoslovak Academy of Sciences Publication No. 70 EUROPEAN REGIONAL ASTRONOMY MEETING OF THE IA U Praha, Czechoslovakia August 24-29, 1987 ASTROPHYSICS Edited by PETR HARMANEC Proceedings, Vol. 1987 Publications of the Astronomical Institute of the Czechoslovak Academy of Sciences Publication No. 70 EUROPEAN REGIONAL ASTRONOMY MEETING OF THE I A U 10 Praha, Czechoslovakia August 24-29, 1987 ASTROPHYSICS Edited by PETR HARMANEC Proceedings, Vol. 5 1 987 CHIEF EDITOR OF THE PROCEEDINGS: LUBOS PEREK Astronomical Institute of the Czechoslovak Academy of Sciences 251 65 Ondrejov, Czechoslovakia TABLE OF CONTENTS Preface HI Invited discourse 3.-C. Pecker: Fran Tycho Brahe to Prague 1987: The Ever Changing Universe 3 lorlishdp on rapid variability of single, binary and Multiple stars A. Baglln: Time Scales and Physical Processes Involved (Review Paper) 13 Part 1 : Early-type stars P. Koubsfty: Evidence of Rapid Variability in Early-Type Stars (Review Paper) 25 NSV. Filtertdn, D.B. Gies, C.T. Bolton: The Incidence cf Absorption Line Profile Variability Among 33 the 0 Stars (Contributed Paper) R.K. Prinja, I.D. Howarth: Variability In the Stellar Wind of 68 Cygni - Not "Shells" or "Puffs", 39 but Streams (Contributed Paper) H. Hubert, B. Dagostlnoz, A.M. Hubert, M. Floquet: Short-Time Scale Variability In Some Be Stars 45 (Contributed Paper) G. talker, S. Yang, C. McDowall, G. Fahlman: Analysis of Nonradial Oscillations of Rapidly Rotating 49 Delta Scuti Stars (Contributed Paper) C. Sterken: The Variability of the Runaway Star S3 Arietis (Contributed Paper) S3 C. Blanco, A. -

Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Presenting Author Title 0. # Amado, Pedro J. Mode identification using 1. simultaneous optical and NIR spectroscopy Ando, Hiroyasu et Detection of Solar-like Oscillations 2. al. in 4 G-giants by precise radial velocity measurement and their characteristics Antoci, Vichi et al. The delta Scuti star Rho Puppis: 3. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Barcza, Szabolcs and Physical parameters of RR Lyrae 4. Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical 5. treatment of the modulated RR Lyrae stars Bernard, Edouard for The ACS LCID Project: Short- 6. the LCID Team period variables Bouabid, Mehdi- Frequency analysis of the SISMO 7. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid 8. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Cameron, Chris et Asteroseismic tuning of the 9. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the 10. al. MOST asteroseismic potential Cash, Jennifer et al. A Long Term Photometric and 11. Spectroscopic Study of RV Tauri stars Chadid, Merieme et First light curves from Antarctica: 12. al. PAIX monitoring of the Blazhko stars Chavez, Joy M. et al. A Cepheid Distance to the 13. Antennae De Cat, Peter et al. Is HD147787 a double-lined 14. binary with two pulsating components? De Cat, Peter et al. Towards asteroseismology of 15. main-sequence g-mode pulsators: spectroscopic multi- site campaigns for slowly pulsating B stars and gamma Doradus stars. -

Binocular Certificate Handbook
Irish Federation of Astronomical Societies Binocular Certificate Handbook How to see 110 extraordinary celestial sights with an ordinary pair of binoculars © John Flannery, South Dublin Astronomical Society, August 2004 No ordinary binoculars! This photograph by the author is of the delightfully whimsical frontage of the Chiat/Day advertising agency building on Main Street, Venice, California. Binocular Certificate Handbook page 1 IFAS — www.irishastronomy.org Introduction HETHER NEW to the hobby or advanced am- Wateur astronomer you probably already own Binocular Certificate Handbook a pair of a binoculars, the ideal instrument to casu- ally explore the wonders of the Universe at any time. Name _____________________________ Address _____________________________ The handbook you hold in your hands is an intro- duction to the realm far beyond the Solar System — _____________________________ what amateur astronomers call the “deep sky”. This is the abode of galaxies, nebulae, and stars in many _____________________________ guises. It is here that we set sail from Earth and are Telephone _____________________________ transported across many light years of space to the wonderful and the exotic; dense glowing clouds of E-mail _____________________________ gas where new suns are being born, star-studded sec- tions of the Milky Way, and the ghostly light of far- Observing beginner/intermediate/advanced flung galaxies — all are within the grasp of an ordi- experience (please circle one of the above) nary pair of binoculars. Equipment __________________________________ True, the fixed magnification of (most) binocu- IFAS club __________________________________ lars will not allow you get the detail provided by telescopes but their wide field of view is perfect for NOTES: Details will be treated in strictest confidence. -

Communications in Asteroseismology
Communications in Asteroseismology Volume 142 December, 2002 16th Delta Scuti Star Newsletter for Delta Scuti, Gamma Dor and SX Phe stars Editor: Michel Breger, TurkÄ enschanzstra¼e 17, A - 1180 Wien, Austria Layout and Production: Wolfgang Zima Editorial Board: Gerald Handler, Don Kurtz, Jaymie Matthews, Ennio Poretti http://www.deltascuti.net COVER ILLUSTRATION: Instability domains in the upper part of the Hertzsprung-Russel Diagram. Slowly Pulsating B stars are unstable only to nonradial high-order gravity modes. A similar instability was found for massive stars in addition to the ¯ Cep{type instability. For the classical instability strip, only the Blue Edge is shown. A few evolutionary tracks for the indicated values of M=M¯ are shown. The location of γ Dor variables and of stars with solar-like oscillation is also shown. The position of the present Sun is marked by the symbol ¯. For more information please see the article by A. A. Pamyatnykh on p. 10. British Library Cataloguing in Publication data. A Catalogue record for this book is available from the British Library. All rights reserved ISBN 3-7001-3137-2 ISSN 1021-2043 Copyright °c 2002 by Austrian Academy of Sciences Vienna Contents Editorial 4 First results from a multisite campaign on AV Cet by T. H. Dall, G. Handler, and M. B. Moalusi 6 Comments on the upper main-sequence instability domains by A. A. Pamyatnykh 10 A ¯ve-month multitechnique, multisite campaign on the ¯ Cephei star º Eridani by G. Handler & C. Aerts 20 1994 multisite photometry of the ± Scuti star θ2 Tau by M. -

Development of a Method for Calculating Delta Scuti Rotational Velocities and Hydrogen Beta Color Indices
Brigham Young University BYU ScholarsArchive Theses and Dissertations 2007-09-06 Development of a Method for Calculating Delta Scuti Rotational Velocities and Hydrogen Beta Color Indices Tabitha Christi Buehler Brigham Young University - Provo Follow this and additional works at: https://scholarsarchive.byu.edu/etd Part of the Astrophysics and Astronomy Commons, and the Physics Commons BYU ScholarsArchive Citation Buehler, Tabitha Christi, "Development of a Method for Calculating Delta Scuti Rotational Velocities and Hydrogen Beta Color Indices" (2007). Theses and Dissertations. 1538. https://scholarsarchive.byu.edu/etd/1538 This Thesis is brought to you for free and open access by BYU ScholarsArchive. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of BYU ScholarsArchive. For more information, please contact [email protected], [email protected]. DEVELOPMENT OF A METHOD FOR CALCULATING DELTA SCUTI ROTATIONAL VELOCITIES AND HYDROGEN-BETA COLOR INDICES by Tabitha Christi Bush A thesis submitted to the faculty of Brigham Young University in partial fulfillment of the requirements for the degree of Master of Science Department of Physics and Astronomy Brigham Young University December 2007 Copyright c 2007 Tabitha Christi Bush All Rights Reserved BRIGHAM YOUNG UNIVERSITY GRADUATE COMMITTEE APPROVAL of a thesis submitted by Tabitha Christi Bush This thesis has been read by each member of the following graduate committee and by majority vote has been found to be satisfactory. Date Eric