DOCSLIB.ORG

APPROXIMATE BAYESIAN MODEL SELECTION with the DEVIANCE 3 Residual Variance in a Linear Model) in Θ Θ

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
APPROXIMATE BAYESIAN MODEL SELECTION with the DEVIANCE 3 Residual Variance in a Linear Model) in Θ Θ Statistical Science 2015, Vol. 30, No. 2, 242–257 DOI: 10.1214/14-STS510 c Institute of Mathematical Statistics, 2015 Approximate Bayesian Model Selection with the Deviance Statistic Leonhard Held, Daniel Saban´es Bov´eand Isaac Gravestock Abstract. Bayesian model selection poses two main challenges: the specification of parameter priors for all models, and the computation of the resulting Bayes factors between models. There is now a large literature on automatic and objective parameter priors in the linear model. One important class are g-priors, which were recently extended from linear to generalized linear models (GLMs). We show that the resulting Bayes factors can be approximated by test-based Bayes fac- tors (Johnson [Scand. J. Stat. 35 (2008) 354–368]) using the deviance statistics of the models. To estimate the hyperparameter g, we propose empirical and fully Bayes approaches and link the former to minimum Bayes factors and shrinkage estimates from the literature. Furthermore, we describe how to approximate the corresponding posterior distribu- tion of the regression coefficients based on the standard GLM output. We illustrate the approach with the development of a clinical prediction model for 30-day survival in the GUSTO-I trial using logistic regres- sion. Key words and phrases: Bayes factor, deviance, generalized linear model, g-prior, model selection, shrinkage. 1. INTRODUCTION et al. (1995)]. We study a publicly available sub- group from the Western region of the USA with The problem of model and variable selection is n = 2188 patients and prognosis of the binary end- pervasive in statistical practice. For example, it is point 30-day survival [Steyerberg (2009)]. In order central for the development of clinical prediction to develop a clinical prediction model for this end- models [Steyerberg (2009)]. For illustration, we con- point, we focus our analysis on the assessment of the arXiv:1308.6780v3 [stat.ME] 18 Aug 2015 sider the GUSTO-I trial, a large randomized study effects of 17 covariates listed in Table 1 in a logistic for comparison of four different treatments in over regression model. 40,000 acute myocardial infarction patients [Lee There is now a large literature on automatic and objective Bayesian model selection, which unburden Leonhard Held is Professor and Isaac Gravestock is the statistician from eliciting manually the parame- Ph.D. Student, Department of Biostatistics, Institute of Epidemiology, Biostatistics and Prevention, University ter priors for all models in the absence of substan- of Zurich, Hirschengraben 84, 8001 Zurich, Switzerland tive prior information [see, e.g., Berger and Pericchi e-mail: [email protected]; [email protected]. (2001)]. However, such objective Bayesian method- Daniel Saban´es Bov´eis Biostatistician at F. ology is currently limited to the linear model [e.g., Hoffmann-La Roche Ltd, 4070 Basel, Switzerland Bayarri et al. (2012)], where the g-prior on the re- e-mail: daniel.sabanes [email protected]. gression coefficients is the standard choice [Liang This is an electronic reprint of the original article et al. (2008)]. For non-Gaussian regression, there are published by the Institute of Mathematical Statistics in computational and conceptual problems, and one so- Statistical Science, 2015, Vol. 30, No. 2, 242–257. This lution to this are test-based Bayes factors [John- reprint differs from the original in pagination and son (2005)]. Consider a classical scenario with a typographic detail. null model nested within a more general alternative 1 2 L. HELD, D. SABANES´ BOVE´ AND I. GRAVESTOCK Table 1 Description of the variables in the GUSTO-I data set Variable Description y Death within 30 days after acute myocardial infarction (Yes =1, No=0) x1 Gender (Female = 1, Male = 0) x2 Age [years] x3 Killip class (4 categories) x4 Diabetes (Yes = 1, No = 0) x5 Hypotension (Yes = 1, No = 0) x6 Tachycardia (Yes = 1, No = 0) x7 Anterior infarct location (Yes = 1, No = 0) x8 Previous myocardial infarction (Yes = 1, No = 0) x9 Height [cm] x10 Weight [kg] x11 Hypertension history (Yes = 1, No = 0) x12 Smoking (3 categories: Never/Ex/Current) x13 Hypercholesterolaemia (Yes = 1, No = 0) x14 Previous angina pectoris (Yes = 1, No = 0) x15 Family history of myocardial infarctions (Yes = 1, No = 0) x16 ST elevation on ECG: Number of leads (0–11) x17 Time to relief of chest pain more than 1 hour (Yes = 1, No = 0) model. Traditionally, the use of Bayes factors re- we finally obtain a unified framework for objective quires the specification of proper prior distributions Bayesian model selection and parameter inference on all unknown model parameters of the alternative for GLMs. model, which are not shared by the null model. In The paper is structured as follows. In Section 2 contrast, Johnson (2005) defines Bayes factors us- we review the g-prior in the linear and generalized ing the distribution of a suitable test statistic under linear model, and show that this prior choice is im- the null and alternative models, effectively replacing plicit in the application of test-based Bayes factors the data with the test statistic. This approach elim- computed from the deviance statistic. In Section 3 inates the necessity to define prior distributions on we describe how the hyperparameter g influences model parameters and leads to simple closed-form model selection and parameter inference, and intro- expressions for χ2-, F -, t-, and z-statistics. duce empirical and fully Bayesian inference for it. The Johnson (2005) approach is extended in John- Using empirical Bayes to estimate g, we are able son (2008) to the likelihood ratio test statistic and, to analytically quantify the accuracy of test-based thus, if applied to generalized linear regression mod- Bayes factors in the linear model. Connections to the els (GLMs), to the deviance statistic [Nelder and literature on minimum Bayes factors and shrinkage Wedderburn (1972)]. This is explored further in Hu of regression coefficients are outlined. In Section 4 and Johnson (2009), where Markov chain Monte we apply the methodology in order to build a logis- Carlo (MCMC) is used to develop a Bayesian vari- tic regression model for predicting 30-day survival able selection algorithm for logistic regression. How- in the GUSTO-I trial, and compare our methodol- ever, the factor g in the implicit g-prior is treated as ogy with selected alternatives in a bootstrap study. fixed and estimation of the regression coefficients is In Section 5 we summarize our findings and sketch also not discussed. We fill this gap and extend the possible extensions. work by Hu and Johnson (2009), combining g-prior methodology for the linear model with Bayesian 2. OBJECTIVE BAYESIAN MODEL SELECTION IN REGRESSION model selection based on the deviance. This enables us to apply empirical [George and Foster (2000)] and Consider a generic regression model with linear fully Bayesian [Cui and George (2008)] approaches predictor η = α + x⊤β, from which weM assume that for estimating the hyperparameter g to GLMs. By the outcome y = (y1,...,yn) was generated. We col- linking g-priors to the theory on shrinkage esti- lect the intercept α, the regression coefficients vec- mates of regression coefficients [Copas (1983, 1997)], tor β, and possible additional parameters (e.g., the APPROXIMATE BAYESIAN MODEL SELECTION WITH THE DEVIANCE 3 residual variance in a linear model) in θ Θ. Spe- 2.1.1 Gaussian linear model Consider the Gaus- ∈ ⊤ 2 cific candidate models , j , differ with respect sian linear model j : yi N(α + x β ,σ ) with Mj ∈J M ∼ ij j to the content and the dimension of the covariate intercept α, regression coefficients vector βj, and 2 vector x, and hence β, so each model j defines variance σ , and collect all parameters in θj = θ M ⊤ 2 ⊤ 2 its own parameter vector j with likelihood func- (α, βj ,σ ) . Here N(µ,σ ) denotes the univariate tion p(y θ , ). 2 | j Mj Gaussian density with mean µ and variance σ , and Through optimizing this likelihood, we obtain the x = (x ,...,x )⊤ is the covariate vector for ob- ˆ ij i1 idj maximum likelihood estimate (MLE) θj of θj. For servation i = 1,...,n. Using the n dj full rank de- ⊤ × Bayesian inference a prior distribution with den- sign matrix Xj = (x1j,..., xnj) , the likelihood ob- sity p(θj j) is assigned to the parameter vector tained from n independent observations is |M θj to obtain the posterior density p(θj y, j) 2 | M ∝ (2) p(y θj, j) = Nn(y α1 + Xjβ ,σ I), p(y θj, j)p(θj j). This forms the basis to com- | M | j | M |M E pute the posterior mean (θj y, j) and other suit- with 1 and I denoting the all-ones vector and iden- | M able characteristics of the posterior distribution. tity matrix of dimension n, respectively. We assume The marginal likelihood that the covariates have been centered around 0, ⊤ that is, Xj 1 = 0. Here and in the following, 0 de- p(y j)= p(y θj, j)p(θj j) dθj notes the zero vector of length dj. |M Θ | M |M Z j Zellner’s g-prior [Zellner (1986)] fixes a constant is the key ingredient to transform prior model prob- g> 0 and specifies the Gaussian prior abilities Pr( j), j , to posterior model proba- 2 2 ⊤ −1 (3) β σ , j Nd (0,gσ (X Xj) ) bilities M ∈J j| M ∼ j j 2 for the regression coefficients βj , conditional on σ . p(y j) Pr( j) Pr( y)= |M M This prior can be interpreted as a posterior distribu- j p(y ) Pr( ) M | k∈J k k β (1) |M M tion, if α is fixed and a locally uniform prior for j is P DBFj,0 Pr( j) combined with an imaginary outcome y0 = α1 from = MPr .
Load more

Recommended publications
  • Fast Computation of the Deviance Information Criterion for Latent Variable Models
    Crawford School of Public Policy CAMA Centre for Applied Macroeconomic Analysis Fast Computation of the Deviance Information Criterion for Latent Variable Models CAMA Working Paper 9/2014 January 2014 Joshua C.C. Chan Research School of Economics, ANU and Centre for Applied Macroeconomic Analysis Angelia L. Grant Centre for Applied Macroeconomic Analysis Abstract The deviance information criterion (DIC) has been widely used for Bayesian model comparison. However, recent studies have cautioned against the use of the DIC for comparing latent variable models. In particular, the DIC calculated using the conditional likelihood (obtained by conditioning on the latent variables) is found to be inappropriate, whereas the DIC computed using the integrated likelihood (obtained by integrating out the latent variables) seems to perform well. In view of this, we propose fast algorithms for computing the DIC based on the integrated likelihood for a variety of high- dimensional latent variable models. Through three empirical applications we show that the DICs based on the integrated likelihoods have much smaller numerical standard errors compared to the DICs based on the conditional likelihoods. THE AUSTRALIAN NATIONAL UNIVERSITY Keywords Bayesian model comparison, state space, factor model, vector autoregression, semiparametric JEL Classification C11, C15, C32, C52 Address for correspondence: (E) [email protected] The Centre for Applied Macroeconomic Analysis in the Crawford School of Public Policy has been established to build strong links between professional macroeconomists. It provides a forum for quality macroeconomic research and discussion of policy issues between academia, government and the private sector. The Crawford School of Public Policy is the Australian National University’s public policy school, serving and influencing Australia, Asia and the Pacific through advanced policy research, graduate and executive education, and policy impact.
    [Show full text]
  • A Generalized Linear Model for Binomial Response Data
    A Generalized Linear Model for Binomial Response Data Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 1 / 46 Now suppose that instead of a Bernoulli response, we have a binomial response for each unit in an experiment or an observational study. As an example, consider the trout data set discussed on page 669 of The Statistical Sleuth, 3rd edition, by Ramsey and Schafer. Five doses of toxic substance were assigned to a total of 20 fish tanks using a completely randomized design with four tanks per dose. Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 2 / 46 For each tank, the total number of fish and the number of fish that developed liver tumors were recorded. d=read.delim("http://dnett.github.io/S510/Trout.txt") d dose tumor total 1 0.010 9 87 2 0.010 5 86 3 0.010 2 89 4 0.010 9 85 5 0.025 30 86 6 0.025 41 86 7 0.025 27 86 8 0.025 34 88 9 0.050 54 89 10 0.050 53 86 11 0.050 64 90 12 0.050 55 88 13 0.100 71 88 14 0.100 73 89 15 0.100 65 88 16 0.100 72 90 17 0.250 66 86 18 0.250 75 82 19 0.250 72 81 20 0.250 73 89 Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 3 / 46 One way to analyze this dataset would be to convert the binomial counts and totals into Bernoulli responses.
    [Show full text]
  • Sociological Theories of Deviance: Definitions & Considerations
    Sociological Theories of Deviance: Definitions & Considerations NCSS Strands: Individuals, Groups, and Institutions Time, Continuity, and Change Grade level: 9-12 Class periods needed: 1.5- 50 minute periods Purpose, Background, and Context Sociologists seek to understand how and why deviance occurs within a society. They do this by developing theories that explain factors impacting deviance on a wide scale such as social frustrations, socialization, social learning, and the impact of labeling. Four main theories have developed in the last 50 years. Anomie: Deviance is caused by anomie, or the feeling that society’s goals or the means to achieve them are closed to the person Control: Deviance exists because of improper socialization, which results in a lack of self-control for the person Differential association: People learn deviance from associating with others who act in deviant ways Labeling: Deviant behavior depends on who is defining it, and the people in our society who define deviance are usually those in positions of power Students will participate in a “jigsaw” where they will become knowledgeable in one theory and then share their knowledge with the rest of the class. After all theories have been presented, the class will use the theories to explain an historic example of socially deviant behavior: Zoot Suit Riots. Objectives & Student Outcomes Students will: Be able to define the concepts of social norms and deviance 1 Brainstorm behaviors that fit along a continuum from informal to formal deviance Learn four sociological theories of deviance by reading, listening, constructing hypotheticals, and questioning classmates Apply theories of deviance to Zoot Suit Riots that occurred in the 1943 Examine the role of social norms for individuals, groups, and institutions and how they are reinforced to maintain a order within a society; examine disorder/deviance within a society (NCSS Standards, p.
    [Show full text]
  • Comparison of Some Chemometric Tools for Metabonomics Biomarker Identification ⁎ Réjane Rousseau A, , Bernadette Govaerts A, Michel Verleysen A,B, Bruno Boulanger C
    Available online at www.sciencedirect.com Chemometrics and Intelligent Laboratory Systems 91 (2008) 54–66 www.elsevier.com/locate/chemolab Comparison of some chemometric tools for metabonomics biomarker identification ⁎ Réjane Rousseau a, , Bernadette Govaerts a, Michel Verleysen a,b, Bruno Boulanger c a Université Catholique de Louvain, Institut de Statistique, Voie du Roman Pays 20, B-1348 Louvain-la-Neuve, Belgium b Université Catholique de Louvain, Machine Learning Group - DICE, Belgium c Eli Lilly, European Early Phase Statistics, Belgium Received 29 December 2006; received in revised form 15 June 2007; accepted 22 June 2007 Available online 29 June 2007 Abstract NMR-based metabonomics discovery approaches require statistical methods to extract, from large and complex spectral databases, biomarkers or biologically significant variables that best represent defined biological conditions. This paper explores the respective effectiveness of six multivariate methods: multiple hypotheses testing, supervised extensions of principal (PCA) and independent components analysis (ICA), discriminant partial least squares, linear logistic regression and classification trees. Each method has been adapted in order to provide a biomarker score for each zone of the spectrum. These scores aim at giving to the biologist indications on which metabolites of the analyzed biofluid are potentially affected by a stressor factor of interest (e.g. toxicity of a drug, presence of a given disease or therapeutic effect of a drug). The applications of the six methods to samples of 60 and 200 spectra issued from a semi-artificial database allowed to evaluate their respective properties. In particular, their sensitivities and false discovery rates (FDR) are illustrated through receiver operating characteristics curves (ROC) and the resulting identifications are used to show their specificities and relative advantages.The paper recommends to discard two methods for biomarker identification: the PCA showing a general low efficiency and the CART which is very sensitive to noise.
    [Show full text]
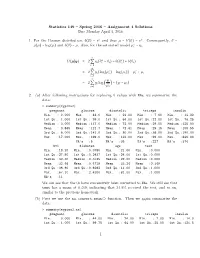
  • Statistics 149 – Spring 2016 – Assignment 4 Solutions Due Monday April 4, 2016 1. for the Poisson Distribution, B(Θ) =
    Statistics 149 { Spring 2016 { Assignment 4 Solutions Due Monday April 4, 2016 1. For the Poisson distribution, b(θ) = eθ and thus µ = b′(θ) = eθ. Consequently, θ = ∗ g(µ) = log(µ) and b(θ) = µ. Also, for the saturated model µi = yi. n ∗ ∗ D(µSy) = 2 Q yi(θi − θi) − b(θi ) + b(θi) i=1 n ∗ ∗ = 2 Q yi(log(µi ) − log(µi)) − µi + µi i=1 n yi = 2 Q yi log − (yi − µi) i=1 µi 2. (a) After following instructions for replacing 0 values with NAs, we summarize the data: > summary(mypima2) pregnant glucose diastolic triceps insulin Min. : 0.000 Min. : 44.0 Min. : 24.00 Min. : 7.00 Min. : 14.00 1st Qu.: 1.000 1st Qu.: 99.0 1st Qu.: 64.00 1st Qu.:22.00 1st Qu.: 76.25 Median : 3.000 Median :117.0 Median : 72.00 Median :29.00 Median :125.00 Mean : 3.845 Mean :121.7 Mean : 72.41 Mean :29.15 Mean :155.55 3rd Qu.: 6.000 3rd Qu.:141.0 3rd Qu.: 80.00 3rd Qu.:36.00 3rd Qu.:190.00 Max. :17.000 Max. :199.0 Max. :122.00 Max. :99.00 Max. :846.00 NA's :5 NA's :35 NA's :227 NA's :374 bmi diabetes age test Min. :18.20 Min. :0.0780 Min. :21.00 Min. :0.000 1st Qu.:27.50 1st Qu.:0.2437 1st Qu.:24.00 1st Qu.:0.000 Median :32.30 Median :0.3725 Median :29.00 Median :0.000 Mean :32.46 Mean :0.4719 Mean :33.24 Mean :0.349 3rd Qu.:36.60 3rd Qu.:0.6262 3rd Qu.:41.00 3rd Qu.:1.000 Max.
    [Show full text]
  • Deviance from Social Norms: Who Are the Deviants?
    Running Head: DEVIANCE FROM SOCIAL NORMS: WHO ARE THE DEVIANTS? This article was published in the Journal of Social and Political Psychology doi: https://doi.org/10.5964/jspp.v8i1.1134 The Social and Psychological Characteristics of Norm Deviants: A Field Study in a Small Cohesive University Campus Robin Gomila and Elizabeth Levy Paluck Princeton University Word count: 10,342 DEVIANCE FROM SOCIAL NORMS: WHO ARE THE DEVIANTS? Abstract People who deviate from the established norms of their social group can clarify group boundaries, strengthen group cohesion, and catalyze group and broader social change. Yet social psychologists have recently neglected the study of deviants. We conducted in-depth interviews of Princeton University upperclassmen who deviated from a historical and widely known Princeton norm: joining an “eating club,” a social group that undergraduates join at the end of their sophomore year. We explored the themes of these interviews with two rounds of surveys during the semester when students decide whether to join an eating club (pilot survey, N=408; and a random subsample of the pilot survey with 90% takeup, N=212). The surveys asked: what are the social and psychological antecedents of deviance from norms? The data suggest that deviance is a pattern: compared to those who conform, students who deviate by not joining clubs report a history of deviance and of feeling different from the typical member of their social group. They also feel less social belonging and identification with Princeton and its social environment. Students who deviate are lower in social monitoring, but otherwise are comparable to students who conform in terms of personality traits measured by the Big Five, and of their perception of the self as socially awkward, independent, or rebellious.
    [Show full text]
  • Bayesian Methods: Review of Generalized Linear Models
    Bayesian Methods: Review of Generalized Linear Models RYAN BAKKER University of Georgia ICPSR Day 2 Bayesian Methods: GLM [1] Likelihood and Maximum Likelihood Principles Likelihood theory is an important part of Bayesian inference: it is how the data enter the model. • The basis is Fisher’s principle: what value of the unknown parameter is “most likely” to have • generated the observed data. Example: flip a coin 10 times, get 5 heads. MLE for p is 0.5. • This is easily the most common and well-understood general estimation process. • Bayesian Methods: GLM [2] Starting details: • – Y is a n k design or observation matrix, θ is a k 1 unknown coefficient vector to be esti- × × mated, we want p(θ Y) (joint sampling distribution or posterior) from p(Y θ) (joint probabil- | | ity function). – Define the likelihood function: n L(θ Y) = p(Y θ) | i| i=1 Y which is no longer on the probability metric. – Our goal is the maximum likelihood value of θ: θˆ : L(θˆ Y) L(θ Y) θ Θ | ≥ | ∀ ∈ where Θ is the class of admissable values for θ. Bayesian Methods: GLM [3] Likelihood and Maximum Likelihood Principles (cont.) Its actually easier to work with the natural log of the likelihood function: • `(θ Y) = log L(θ Y) | | We also find it useful to work with the score function, the first derivative of the log likelihood func- • tion with respect to the parameters of interest: ∂ `˙(θ Y) = `(θ Y) | ∂θ | Setting `˙(θ Y) equal to zero and solving gives the MLE: θˆ, the “most likely” value of θ from the • | parameter space Θ treating the observed data as given.
    [Show full text]
  • A Conceptual Overview of Deviance and Its Implication to Mental Health
    International Journal of Humanities and Social Science Invention ISSN (Online): 2319 – 7722, ISSN (Print): 2319 – 7714 www.ijhssi.org || Volume 2 Issue 12 || December. 2013 || PP.01-09 A Conceptual Overview of Deviance and Its Implication to Mental Health: a Bio psychosocial Perspective Nalah, Augustine Bala1, Ishaya, Leku Daniel2 1-Behavioural Health Unit, Psychology Department, Faculty of Social Sciences, Nasarawa State University, Keffi – Nigeria; 2- Department of Sociology, Faculty of Social Sciences, Nasarawa State University, Keffi –Nigeria; ABSTRACT: This research paper is a conceptual overview of deviance and its implications to mental health and well-being. The study conceptualized and theorized deviance and mental health through the sociological, biological, and psychological dimensions. All theories agreed that deviant behaviour begins from childhood through old-age. This suggests a deviation from behaviour appropriate to the laws or norms and values of a particular society. This makes deviance to be relative, depending on the society and individual. Mental illness and Post-Traumatic-Stress-Disorder (PTSD) as the inflicted or labelled deviants are unable to cope. The behavioural aftermath of PTSD typically involves increased aggression and drug and alcohol abuse, which could lead to anxiety, depression, insomnia, plus memory and cognitive impairments or mental disorder. The paper recommends policymakers in collaboration with behavioural health specialists (Clinical psychologists), should focus on developing and implementing social learning preventive and reformative programmes through role playing, behaviour modification, social support system, and peer and group psychotherapy among others. Keywords: Conduct disorder, deviance, mental health, post-traumatic-stress-disorder, psychological trauma, I. INTRODUCTION The social understanding of the study of deviance and crime examine cultural norms; how they change over time, how they are enforced, and what happens to individuals and societies when norms are broken.
    [Show full text]
  • What I Should Have Described in Class Today
    Statistics 849 Clarification 2010-11-03 (p. 1) What I should have described in class today Sorry for botching the description of the deviance calculation in a generalized linear model and how it relates to the function dev.resids in a glm family object in R. Once again Chen Zuo pointed out the part that I had missed. We need to use positive contributions to the deviance for each observation if we are later to take the square roots of these quantities. To ensure that these are all positive we establish a baseline level for the deviance, which is the lowest possible value of the deviance, corresponding to a saturated model in which each observation has one parameter associated with it. Another value quoted in the summary output is the null deviance, which is the deviance for the simplest possible model (the \null model") corresponding to a formula like > data(Contraception, package = "mlmRev") > summary(cm0 <- glm(use ~ 1, binomial, Contraception)) Call: glm(formula = use ~ 1, family = binomial, data = Contraception) Deviance Residuals: Min 1Q Median 3Q Max -0.9983 -0.9983 -0.9983 1.3677 1.3677 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -0.43702 0.04657 -9.385 <2e-16 (Dispersion parameter for binomial family taken to be 1) Null deviance: 2590.9 on 1933 degrees of freedom Residual deviance: 2590.9 on 1933 degrees of freedom AIC: 2592.9 Number of Fisher Scoring iterations: 4 Notice that the coefficient estimate, -0.437022, is the logit transformation of the proportion of positive responses > str(y <- as.integer(Contraception[["use"]]) - 1L) int [1:1934] 0 0 0 0 0 0 0 0 0 0 ..
    [Show full text]
  • Theories and Methods in Deviance Studies
    SECTION THEORIES AND 1 METHODS IN DEVIANCE STUDIES This page intentionally left blank CHAPTER Views of 1 Deviance Witches’ Sabbath, woodcut by German artist Hans Baldung “Grien” (1510, Ivy Close Images/Alamy Stock Photo). CONTENTS LEARNING OBJECTIVES Introduction 4 After reading this chapter, you will be able to: Blurred Boundaries: The Drama of Deviance 4 ᭤ Deviance as Demonic 6 Defi ne deviance in sociological terms ᭤ Recognize “blurred boundaries” as a key Deviance as Psychotic 8 feature of deviance Deviance as Exotic 10 ᭤ Describe three “popular” explanations of Deviance as Symbolic Interaction: A Sociological deviance Approach 12 ᭤ Explain the sociological approach to Social Acts 13 studying deviance Focus on Observable Behavior 14 ᭤ Summarize the importance of a sociologi- Symbolic Interaction 16 cal understanding of deviance The Sociological Promise 17 Summary 18 Keywords 19 3 4 Chapter 1 | Views of Deviance INTRODUCTION Virtually all humans make distinctions between right and wrong, good and bad, normal and weird. It is hard to imagine that we could be human—or sur- vive as a species—without making such distinctions. Th e sociology of deviance is devoted to studying the “bad,” “wrong,” and “weird” side of these divisions: what people consider immoral, criminal, strange, and disgusting. Deviance includes the broadest possible scope of such activities—not just criminal acts, but also any actions, thoughts, feelings, or social statuses that members of a social group judge to be a violation of their values or rules. Th is book provides a sociological understanding of deviance, as well as examines many of the major categories of deviance in contemporary American society.
    [Show full text]
  • John Snow, Cholera and the Mystery of the Broad Street Pump PDF Book Well Written and Easy to Read, Despite of the Heavy Subject
    THE MEDICAL DETECTIVE: JOHN SNOW, CHOLERA AND THE MYSTERY OF THE BROAD STREET PUMP PDF, EPUB, EBOOK Sandra Hempel | 304 pages | 06 Aug 2007 | GRANTA BOOKS | 9781862079373 | English | London, United Kingdom The Medical Detective: John Snow, Cholera and the Mystery of the Broad Street Pump PDF Book Well written and easy to read, despite of the heavy subject. When people didb't believe the doctor who proposed the answer and suggested a way to stop the spread of such a deadly disease, I wanted to scream in frustration! He first published his theory in an essay, On the Mode of Communication of Cholera , [21] followed by a more detailed treatise in incorporating the results of his investigation of the role of the water supply in the Soho epidemic of Snow did not approach cholera from a scientific point of view. Sandra Hempel. John Snow. The city had widened the street and the cesspit was lost. He showed that homes supplied by the Southwark and Vauxhall Waterworks Company , which was taking water from sewage-polluted sections of the Thames , had a cholera rate fourteen times that of those supplied by Lambeth Waterworks Company , which obtained water from the upriver, cleaner Seething Wells. Sandra Hempel did a fantastic job with grabbing attention of the reader and her experience with journalism really shows itself in this book. He then repeated the procedure for the delivery of her daughter three years later. View 2 comments. Episode 6. The author did a wonderful job of keeping me interested in what could have been a fairly dry subject.
    [Show full text]
  • The Deviance Information Criterion: 12 Years On
    J. R. Statist. Soc. B (2014) The deviance information criterion: 12 years on David J. Spiegelhalter, University of Cambridge, UK Nicola G. Best, Imperial College School of Public Health, London, UK Bradley P. Carlin University of Minnesota, Minneapolis, USA and Angelika van der Linde Bremen, Germany [Presented to The Royal Statistical Society at its annual conference in a session organized by the Research Section on Tuesday, September 3rd, 2013, Professor G. A.Young in the Chair ] Summary.The essentials of our paper of 2002 are briefly summarized and compared with other criteria for model comparison. After some comments on the paper’s reception and influence, we consider criticisms and proposals for improvement made by us and others. Keywords: Bayesian; Model comparison; Prediction 1. Some background to model comparison Suppose that we have a given set of candidate models, and we would like a criterion to assess which is ‘better’ in a defined sense. Assume that a model for observed data y postulates a density p.y|θ/ (which may include covariates etc.), and call D.θ/ =−2log{p.y|θ/} the deviance, here considered as a function of θ. Classical model choice uses hypothesis testing for comparing nested models, e.g. the deviance (likelihood ratio) test in generalized linear models. For non- nested models, alternatives include the Akaike information criterion AIC =−2log{p.y|θˆ/} + 2k where θˆ is the maximum likelihood estimate and k is the number of parameters in the model (dimension of Θ). AIC is built with the aim of favouring models that are likely to make good predictions.
    [Show full text]