DOCSLIB.ORG

Robust Dose-Response Curve Estimation Applied to High Content

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Robust Dose-Response Curve Estimation Applied to High Content Nguyen et al. Source Code for Biology and Medicine 2014, 9:27 http://www.scfbm.org/content/9/1/27 RESEARCH Open Access Robust dose-response curve estimation applied to high content screening data analysis Thuy Tuong Nguyen2*, Kyungmin Song5, Yury Tsoy1,JinYeopKim1,Yong-JunKwon3,MyungjooKang5 and Michael Adsetts Edberg Hansen4* Abstract Background and method: Successfully automated sigmoidal curve fitting is highly challenging when applied to large data sets. In this paper, we describe a robust algorithm for fitting sigmoid dose-response curves by estimating four parameters (floor, window, shift, and slope), together with the detection of outliers. We propose two improvements over current methods for curve fitting. The first one is the detection of outliers which is performed during the initialization step with correspondent adjustments of the derivative and error estimation functions. The second aspect is the enhancement of the weighting quality of data points using mean calculation in Tukeys biweight function. Results and conclusion: Automatic curve fitting of 19,236 dose-response experiments shows that our proposed method outperforms the current fitting methods provided by MATLABsnlinfit function and GraphPads Prism software. Keywords: High content screening, Dose response curve, Curve fitting, Sigmoidal function, Weighting function, Outlier detection Introduction dose-response curves (DRCs) that require proper fitting. In recent years, the need for automatic data analysis has The overall process of fitting, rejecting outliers, and data been amplified by the use of high content screening (HCS) point weighting of thousands to millions of curves can [1] techniques. HCS (also known as phenotypic screening) be a significant challenge. The quality of a dose-response is a great tool to identify small molecules that alter the dis- curve fitting algorithm is a key element that should help in ease state of a cell based on measuring cellular phenotype. reducing false positive hits and increasing real compound However, HCS always comes with an important caveat: hits. there is little or no a priori information on the com- Several solutions [4-9] have been proposed to perform pounds target. At the Institut Pasteur Korea (IP-K), we curve fitting. One of the widely used nonlinear curve fit- have applied high content screening using small interfer- ting algorithms was introduced by Levenberg-Marquardt ing RNA (siRNA) [2,3] at the genome scale. More recently, (LM) [5,6]. This method belongs to the gradient-descent we applied the siRNA knockdown strategy for each gene family. However, due to the sensitivity of the method, the from the genome and studied their effect on a given data quality and the initial guess, the curve fitting algo- molecule producing a clear response on a cellular assay, rithm is unfortunately susceptible to becoming trapped in to look for synergestic effects of a drug and target. Per- local minimums. To obtain proper curve fitting results, forming large-scale curve fitting for the biological activity there is a need for automatic outlier handling, usage of of a large compound library can lead to a great number of predefined initial curves, and adaptive weighting for data points [10,11]. All of these demands can, without doubt, *Correspondence: [email protected]; be applicable to large sets of data. Nonlinear and non- [email protected] Equal contributors iterative least square regression analysis was presented 2University of California, Davis, USA in [7] for robust logistic curve fitting with detection of 4 Videometer A/S, Horsholm, Denmark possible outliers. This non-iterative algorithm was imple- Full list of author information is available at the end of the article mented in a microcomputer and assessed using different 2014 Nguyen et al.; licensee BioMed Central. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated. Nguyen et al. Source Code for Biology and Medicine 2014, 9:27 Page 2 of 9 http://www.scfbm.org/content/9/1/27 biological and medical data. A review of popular fitting the floor - the efficacy - which shows the biological activ- models using linear and nonlinear regression is given ity without a chemical compound; β2 is the window - the in [4]. The study serves as a practical guide to help efficacy - which shows the maximum saturated activity at researchers who are not statisticians understand statistical high concentration; β3 is the shift - the potency - of the tools more clearly, especially dose-response curve fitting DRC; and β4 is the slope - the kinetics. Figure 1 shows an using nonlinear regression. This book also describes the illustration of a response curve and its four parameters. robust fitting algorithm and the outlier detection mecha- nism used in the commercial software GraphPad Prism. Basic computation of curve fitting In [8], an automatic best-of-fit estimation procedure is The goal of a curve fitting algorithm is to solve a statisti- introduced based on the Akaike information criterion. cally optimized model that best fits the data set. Because This best-of-fit model guarantees not only the estimation the DRC function is nonlinear, an iterative method is con- of the parameters with smallest sum-of-squares errors but sidered to optimize parameters. In this section, a basic also good prediction of the model. viewpoint is presented to approach the proposed ideas Simulated data for DRC estimation was used in [9] to in our method. First, let χ be the function of the fit- examine the performance of the proposed Grid algorithm. ting parameter β which will be determined via function The peculiarity of the Grid algorithm is that it visits all minimization: the points in a grid of four curve parameters and searches N y f (x , β) for the point with the optimum sum-of-squares error. A χ(β) = ρ i i ,(2) coarse-to-fine grid model and a threshold-based outlier σ i i detection mechanism were used to make the algorithm more efficient. This paper also provided Java-based soft- where ρ(z) is an error estimation function of a single vari- ware together with a sample dataset for academic use. able z; σ is a normalization value; and N is the number of However, the software is applicable only when the mea- data points. To minimize (2), the Newton method is used surements are taken without replicates (one data point at to search for zero crossing of the gradient: each concentration). Furthermore, various popular com- β = β + 1 ∇ χ(β ) puter software and code packages have been presented t+1 t D [ t ]. (3) for DRC fitting such as the DRC package in R [12], the Hence, we need to find the gradient and the Hessian nlinfit function in MATLAB [13], and the XLfit add- matrix D of χ. The gradient of χ with respect to β = in for Microsoft Excel [14]. {β1, β2, β3, β4} is computed as In this paper, robust fitting and automatic outlier detec- tion based on Tukeys biweight function are introduced. ∂χ N ∂ ( β) = 1 ψ( ) f xi, This method was developed to automate nonlinear fit- ∂β σ z ∂β ,(4) ting of thousands of DRCs performed in replicates, detect k i i k the outliers automatically, and initialize the fitting curves robustly. Background and method Background In drug discovery, analysis of the dose-response curve (DRC) is one of the most important tools for evaluat- ing the effect of a drug on a disease. The DRC can be used to plot the results of many types of assays; its X- axis corresponds to the concentrations of a drug (in log scale), and its Y-axis corresponds to the drug responses. The function of DRC can be varied with different number of parameters, but the four parameter model is the most common: β ( β) = β + 2 f x, 1 β ,(1) 1 + exp 3 x β4 β β β β where x is the dose or concentration of a data point; β Figure 1 A four-parameter dose-response curve. 1, 2, 3,and 4 are the floor, the window, the shift, and the slope, respectively. represents the four parameters β1, β2, β3,andβ4; β1 is Nguyen et al. Source Code for Biology and Medicine 2014, 9:27 Page 3 of 9 http://www.scfbm.org/content/9/1/27 ψ( ) ρ( ) = ( β where z is the derivative function of z with z yi In our problem, we initialize the fitting parameters o f (xi, β))/σi. The Hessian matrix is calculated using (disregarding outliers) by finding the best fitted curve using ∂2χ N ∂ ( β) ∂ ( β) ∂2 ( β) = 1 ψ( ) f xi, f xi, 1 ψ( ) f xi, 2 z z , ∂β ∂β σ ∂β ∂β σi ∂β ∂β k l i i k l k l ρ(z) =|z| and ψ(z) = sign(z) (10) (5) where the second derivative term is negligible compared instead of (8) which is used without outlier detection. to the first derivative. Let Herein, we proposed (10) to reduce the impact of out- ∂2χ ∂χ liers on the fitting results by considering absolute errors akl = and bk = ,(6) ∂βk∂βl ∂βk and sign-only derivatives. The key difference between (10) and (8) is that the derivative function: ψ(z) = sign(z) where a and b are elements of matrices A and B, kl k results in 1 (negative) or 1 (positive), which controls the respectively; then instead of directly inverting the Hessian gradient in the direction of having a higher number of matrix, (3) can be rewritten as a set of linear equations: negatives/positives, whereas ψ(z) = z judges the gradient 4 based on the distance between the estimated and actual δβ = akl l bk,(7)values.
Load more

Recommended publications
  • Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A
    IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 9, NO. 6, JUNE 2000 1075 Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A. T. Figueiredo, Member, IEEE, José M. N. Leitão, Member, IEEE, and Anil K. Jain, Fellow, IEEE Abstract—This paper describes a new approach to adaptive having external/potential energy, which is a func- estimation of parametric deformable contours based on B-spline tion of certain features of the image The equilibrium (min- representations. The problem is formulated in a statistical imal total energy) configuration framework with the likelihood function being derived from a re- gion-based image model. The parameters of the image model, the (1) contour parameters, and the B-spline parameterization order (i.e., the number of control points) are all considered unknown. The is a compromise between smoothness (enforced by the elastic parameterization order is estimated via a minimum description nature of the model) and proximity to the desired image features length (MDL) type criterion. A deterministic iterative algorithm is (by action of the external potential). developed to implement the derived contour estimation criterion. Several drawbacks of conventional snakes, such as their “my- The result is an unsupervised parametric deformable contour: it adapts its degree of smoothness/complexity (number of control opia” (i.e., use of image data strictly along the boundary), have points) and it also estimates the observation (image) model stimulated a great amount of research; although most limitations parameters. The experiments reported in the paper, performed of the original formulation have been successfully addressed on synthetic and real (medical) images, confirm the adequacy and (see, e.g., [6], [9], [10], [34], [38], [43], [49], and [52]), non- good performance of the approach.
    [Show full text]
  • Chapter 26: Mathcad-Data Analysis Functions
    Lecture 3 MATHCAD-DATA ANALYSIS FUNCTIONS Objectives Graphs in MathCAD Built-in Functions for basic calculations: Square roots, Systems of linear equations Interpolation on data sets Linear regression Symbolic calculation Graphing with MathCAD Plotting vector against vector: The vectors must have equal number of elements. MathCAD plots values in its default units. To change units in the plot……? Divide your axis by the desired unit. Or remove the units from the defined vectors Use Graph Toolbox or [Shift-2] Or Insert/Graph from menu Graphing 1 20 2 28 time 3 min Temp 35 K time 4 42 Time min 5 49 40 40 Temp Temp 20 20 100 200 300 2 4 time Time Graphing with MathCAD 1 20 Plotting element by 2 28 element: define a time 3 min Temp 35 K 4 42 range variable 5 49 containing as many i 04 element as each of the vectors. 40 i:=0..4 Temp i 20 100 200 300 timei QuickPlots Use when you want to x 0 0.12 see what a function looks like 1 Create a x-y graph Enter the function on sin(x) 0 y-axis with parameter(s) 1 Enter the parameter on 0 2 4 6 x-axis x Graphing with MathCAD Plotting multiple curves:up to 16 curves in a single graph. Example: For 2 dependent variables (y) and 1 independent variable (x) Press shift2 (create a x-y plot) On the y axis enter the first y variable then press comma to enter the second y variable. On the x axis enter your x variable.
    [Show full text]
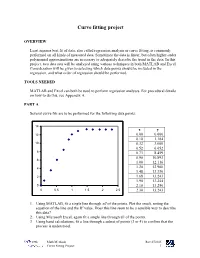
  • Curve Fitting Project
    Curve fitting project OVERVIEW Least squares best fit of data, also called regression analysis or curve fitting, is commonly performed on all kinds of measured data. Sometimes the data is linear, but often higher-order polynomial approximations are necessary to adequately describe the trend in the data. In this project, two data sets will be analyzed using various techniques in both MATLAB and Excel. Consideration will be given to selecting which data points should be included in the regression, and what order of regression should be performed. TOOLS NEEDED MATLAB and Excel can both be used to perform regression analyses. For procedural details on how to do this, see Appendix A. PART A Several curve fits are to be performed for the following data points: 14 x y 12 0.00 0.000 0.10 1.184 10 0.32 3.600 0.52 6.052 8 0.73 8.459 0.90 10.893 6 1.00 12.116 4 1.20 12.900 1.48 13.330 2 1.68 13.243 1.90 13.244 0 2.10 13.250 0 0.5 1 1.5 2 2.5 2.30 13.243 1. Using MATLAB, fit a single line through all of the points. Plot the result, noting the equation of the line and the R2 value. Does this line seem to be a sensible way to describe this data? 2. Using Microsoft Excel, again fit a single line through all of the points. 3. Using hand calculations, fit a line through a subset of points (3 or 4) to confirm that the process is understood.
    [Show full text]
  • Kwame Nkrumah University of Science and Technology, Kumasi
    KWAME NKRUMAH UNIVERSITY OF SCIENCE AND TECHNOLOGY, KUMASI, GHANA Assessing the Social Impacts of Illegal Gold Mining Activities at Dunkwa-On-Offin by Judith Selassie Garr (B.A, Social Science) A Thesis submitted to the Department of Building Technology, College of Art and Built Environment in partial fulfilment of the requirement for a degree of MASTER OF SCIENCE NOVEMBER, 2018 DECLARATION I hereby declare that this work is the result of my own original research and this thesis has neither in whole nor in part been prescribed by another degree elsewhere. References to other people’s work have been duly cited. STUDENT: JUDITH S. GARR (PG1150417) Signature: ........................................................... Date: .................................................................. Certified by SUPERVISOR: PROF. EDWARD BADU Signature: ........................................................... Date: ................................................................... Certified by THE HEAD OF DEPARTMENT: PROF. B. K. BAIDEN Signature: ........................................................... Date: ................................................................... i ABSTRACT Mining activities are undertaken in many parts of the world where mineral deposits are found. In developing nations such as Ghana, the activity is done both legally and illegally, often with very little or no supervision, hence much damage is done to the water bodies where the activities are carried out. This study sought to assess the social impacts of illegal gold mining activities at Dunkwa-On-Offin, the capital town of Upper Denkyira East Municipality in the Central Region of Ghana. The main objectives of the research are to identify factors that trigger illegal mining; to identify social effects of illegal gold mining activities on inhabitants of Dunkwa-on-Offin; and to suggest effective ways in curbing illegal mining activities. Based on the approach to data collection, this study adopts both the quantitative and qualitative approach.
    [Show full text]
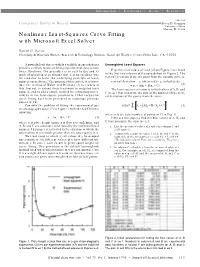
  • Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver
    Information • Textbooks • Media • Resources edited by Computer Bulletin Board Steven D. Gammon University of Idaho Moscow, ID 83844 Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver Daniel C. Harris Chemistry & Materials Branch, Research & Technology Division, Naval Air Warfare Center,China Lake, CA 93555 A powerful tool that is widely available in spreadsheets Unweighted Least Squares provides a simple means of fitting experimental data to non- linear functions. The procedure is so easy to use and its Experimental values of x and y from Figure 1 are listed mode of operation is so obvious that it is an excellent way in the first two columns of the spreadsheet in Figure 2. The for students to learn the underlying principle of least- vertical deviation of the ith point from the smooth curve is squares curve fitting. The purpose of this article is to intro- vertical deviation = yi (observed) – yi (calculated) (2) duce the method of Walsh and Diamond (1) to readers of = yi – (Axi + B/xi + C) this Journal, to extend their treatment to weighted least The least squares criterion is to find values of A, B, and squares, and to add a simple method for estimating uncer- C in eq 1 that minimize the sum of the squares of the verti- tainties in the least-square parameters. Other recipes for cal deviations of the points from the curve: curve fitting have been presented in numerous previous papers (2–16). n 2 Σ Consider the problem of fitting the experimental gas sum = yi ± Axi + B / xi + C (3) chromatography data (17) in Figure 1 with the van Deemter i =1 equation: where n is the total number of points (= 13 in Fig.
    [Show full text]
  • (EU FP7 2013 - 612218/3D-NET) 3DNET Sops HOW-TO-DO PRACTICAL GUIDE
    3D-NET (EU FP7 2013 - 612218/3D-NET) 3DNET SOPs HOW-TO-DO PRACTICAL GUIDE Curve fitting This is intended to be an aid-memoir for those involved in fitting biological data to dose response curves in why we do it and how to best do it. So why do we use non linear regression? Much of the data generated in Biology is sigmoidal dose response (E/[A]) curves, the aim is to generate estimates of upper and lower asymptotes, A50 and slope parameters and their associated confidence limits. How can we analyse E/[A] data? Why fit curves? What’s wrong with joining the dots? Fitting Uses all the data points to estimate each parameter Tell us the confidence that we can have in each parameter estimate Estimates a slope parameter Fitting curves to data is model fitting. The general equation for a sigmoidal dose-response curve is commonly referred to as the ‘Hill equation’ or the ‘four-parameter logistic equation”. (Top Bottom) Re sponse Bottom EC50hillslope 1 [Drug]hillslpoe The models most commonly used in Biology for fitting these data are ‘model 205 – Dose response one site -4 Parameter Logistic Model or Sigmoidal Dose-Response Model’ in XLfit (package used in ActivityBase or Excel) and ‘non-linear regression - sigmoidal variable slope’ in GraphPad Prism. What the computer does - Non-linear least squares Starts with an initial estimated value for each variable in the equation Generates the curve defined by these values Calculates the sum of squares Adjusts the variables to make the curve come closer to the data points (Marquardt method) Re-calculates the sum of squares Continues this iteration until there’s virtually no difference between successive fittings.
    [Show full text]
  • A Grid Algorithm for High Throughput Fitting of Dose-Response Curve Data Yuhong Wang*, Ajit Jadhav, Noel Southal, Ruili Huang and Dac-Trung Nguyen
    Current Chemical Genomics, 2010, 4, 57-66 57 Open Access A Grid Algorithm for High Throughput Fitting of Dose-Response Curve Data Yuhong Wang*, Ajit Jadhav, Noel Southal, Ruili Huang and Dac-Trung Nguyen National Institutes of Health, NIH Chemical Genomics Center, 9800 Medical Center Drive, Rockville, MD 20850, USA Abstract: We describe a novel algorithm, Grid algorithm, and the corresponding computer program for high throughput fitting of dose-response curves that are described by the four-parameter symmetric logistic dose-response model. The Grid algorithm searches through all points in a grid of four dimensions (parameters) and finds the optimum one that corre- sponds to the best fit. Using simulated dose-response curves, we examined the Grid program’s performance in reproduc- ing the actual values that were used to generate the simulated data and compared it with the DRC package for the lan- guage and environment R and the XLfit add-in for Microsoft Excel. The Grid program was robust and consistently recov- ered the actual values for both complete and partial curves with or without noise. Both DRC and XLfit performed well on data without noise, but they were sensitive to and their performance degraded rapidly with increasing noise. The Grid program is automated and scalable to millions of dose-response curves, and it is able to process 100,000 dose-response curves from high throughput screening experiment per CPU hour. The Grid program has the potential of greatly increas- ing the productivity of large-scale dose-response data analysis and early drug discovery processes, and it is also applicable to many other curve fitting problems in chemical, biological, and medical sciences.
    [Show full text]
  • Fitting Conics to Noisy Data Using Stochastic Linearization
    Fitting Conics to Noisy Data Using Stochastic Linearization Marcus Baum and Uwe D. Hanebeck Abstract— Fitting conic sections, e.g., ellipses or circles, to LRF noisy data points is a fundamental sensor data processing problem, which frequently arises in robotics. In this paper, we introduce a new procedure for deriving a recursive Gaussian state estimator for fitting conics to data corrupted by additive Measurements Gaussian noise. For this purpose, the original exact implicit measurement equation is reformulated with the help of suitable Fig. 1: Laser rangefinder (LRF) scanning a circular object. approximations as an explicit measurement equation corrupted by multiplicative noise. Based on stochastic linearization, an efficient Gaussian state estimator is derived for the explicit measurement equation. The performance of the new approach distributions for the parameter vector of the conic based is evaluated by means of a typical ellipse fitting scenario. on Bayes’ rule. An explicit description of the parameter uncertainties with a probability distribution is in particular I. INTRODUCTION important for performing gating, i.e., dismissing unprobable In this work, the problem of fitting a conic section such measurements, and tracking multiple conics. Furthermore, as an ellipse or a circle to noisy data points is considered. the temporal evolution of the state can be captured with This fundamental problem arises in many applications related a stochastic system model, which allows to propagate the to robotics. A traditional application is computer vision, uncertainty about the state to the next time step. where ellipses and circles are fitted to features extracted A. Contributions from images [1]–[4] in order to detect, localize, and track objects.
    [Show full text]
  • Small Molecule Screening Protocols
    Small Molecule Screening Workshop July 29th, 2013 Sapporo, Japan Molecular Biophysics Group Structural Genomics Consortium University of Toronto On the cover: Cytosolic sulfotransferase family of proteins was screened against a library of 90 compounds by a thermodenaturation-based method (DSLS). Structures of cytosolic sulfotransferases are clustered according to their binding site structural similarity and surrounded by the molecules used in the binding experiments (Allali-Hassani et al., 2007, PLoS Biology. PMID: 17425406). Welcome to the workshop As part of the SGC’s ongoing program in structural genomics of human and malaria proteins we are also identifying small molecules that bind and stabilize our proteins, thereby promoting crystallization. We have implemented two screening platforms, based on either fluorimetry or static light scattering, to measure the increase in protein thermal stability upon binding of a ligand without the need to monitor enzyme activity (Vedadi et al (2006) PNAS. 103 (43):15835-40). Identification of small molecules that bind to proteins can provide valuable information on protein specificity, activity, as well as a practical means to facilitate 3D structure determination. This workshop aims to provide an opportunity for you to learn how to implement differential scanning fluorimetry (DSF) technique. We would like to take the opportunity to welcome you to our workshop. Masoud Vedadi Contact Information Masoud Vedadi, Ph.D. Principal Investigator, Molecular Biophysics Structural Genomics Consortium, Assistant Professor, Department of Pharmacology and Toxicology, University of Toronto, MaRS Centre, South Tower 101 College St.7 Floor,Room 714 Toronto, ON, M5G 1L7 Tel: 416 946 0897 E-mail: [email protected] www.sgc.utoronto.ca/biophysics Prepared by: Dr.
    [Show full text]
  • Investigating Bias in the Application of Curve Fitting Programs To
    Atmos. Meas. Tech., 8, 1469–1489, 2015 www.atmos-meas-tech.net/8/1469/2015/ doi:10.5194/amt-8-1469-2015 © Author(s) 2015. CC Attribution 3.0 License. Investigating bias in the application of curve fitting programs to atmospheric time series P. A. Pickers and A. C. Manning Centre for Ocean and Atmospheric Sciences, School of Environmental Sciences, University of East Anglia, Norwich, NR4 7TJ, UK Correspondence to: P. A. Pickers ([email protected]) Received: 31 May 2014 – Published in Atmos. Meas. Tech. Discuss.: 16 July 2014 Revised: 6 November 2014 – Accepted: 6 November 2014 – Published: 23 March 2015 Abstract. The decomposition of an atmospheric time series programs for certain types of data sets, and for certain types into its constituent parts is an essential tool for identifying of analyses and applications. In addition, we recommend that and isolating variations of interest from a data set, and is sensitivity tests are performed in any study using curve fitting widely used to obtain information about sources, sinks and programs, to ensure that results are not unduly influenced by trends in climatically important gases. Such procedures in- the input smoothing parameters chosen. volve fitting appropriate mathematical functions to the data. Our findings also have implications for previous studies However, it has been demonstrated that the application of that have relied on a single curve fitting program to inter- such curve fitting procedures can introduce bias, and thus in- pret atmospheric time series measurements. This is demon- fluence the scientific interpretation of the data sets. We inves- strated by using two other curve fitting programs to replicate tigate the potential for bias associated with the application of work in Piao et al.
    [Show full text]
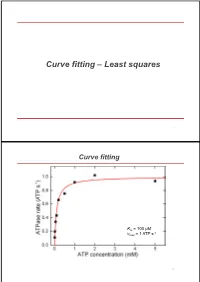
  • Curve Fitting – Least Squares
    Curve fitting – Least squares 1 Curve fitting Km = 100 µM -1 vmax = 1 ATP s 2 Excurse error of multiple measurements Starting point: Measure N times the same parameter Obtained values are Gaussian distributed around mean with standard deviation σ What is the error of the mean of all measurements? Sum = x1 +x2 + ... + xN Variance of sum = N * σ2 (Central limit theorem) Standard deviation of sum N Mean = (x1 +x2 + ... + xN)/N N 1 Standard deviation of mean N (called standard error of mean) N N N 3 Excurse error propagation What is error for f(x,y,z,…) if we know errors of x,y,z,… (σx, σy, σz, …) for purely statistical errors? -> Individual variances add scaled by squared partial derivatives (if parameters are uncorrelated) Examples : Addition/substraction: squared errors add up squared relative Product: errors add up 4 Excurse error propagation squared relative Ratios: errors add up Powers: relative error times power Logarithms: error is relative error 5 Curve fitting – Least squares Starting point: - data set with N pairs of (xi,yi) - xi known exactly, -yi Gaussian distributed around true value with error σi - errors uncorrelated - function f(x) which shall describe the values y (y = f(x)) - f(x) depends on one or more parameters a [S] v vmax [S] KM 6 Curve fitting – Least squares 1 2 2 Probability to get y for given x [y i f (xi ;a)] / 2 i ] i i P(y i ;a) e 2 i [S] v vmax [S] KM 7 Curve fitting – Least squares N 1 2 2 Prob.
    [Show full text]
  • Security Systems Services World Report
    Security Systems Services World Report established in 1974, and a brand since 1981. www.datagroup.org Security Systems Services World Report Database Ref: 56162 This database is updated monthly. Security Systems Services World Report SECURITY SYSTEMS SERVICES WORLD REPORT The Security systems services Report has the following information. The base report has 59 chapters, plus the Excel spreadsheets & Access databases specified. This research provides World Data on Security systems services. The report is available in several Editions and Parts and the contents and cost of each part is shown below. The Client can choose the Edition required; and subsequently any Parts that are required from the After-Sales Service. Contents Description ....................................................................................................................................... 5 REPORT EDITIONS ........................................................................................................................... 6 World Report ....................................................................................................................................... 6 Regional Report ................................................................................................................................... 6 Country Report .................................................................................................................................... 6 Town & Country Report ......................................................................................................................
    [Show full text]