From Sparse to Dense and from Assortative to Disassortative In
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
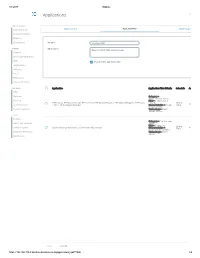
Applications Log Viewer
4/1/2017 Sophos Applications Log Viewer MONITOR & ANALYZE Control Center Application List Application Filter Traffic Shaping Default Current Activities Reports Diagnostics Name * Mike App Filter PROTECT Description Based on Block filter avoidance apps Firewall Intrusion Prevention Web Enable Micro App Discovery Applications Wireless Email Web Server Advanced Threat CONFIGURE Application Application Filter Criteria Schedule Action VPN Network Category = Infrastructure, Netw... Routing Risk = 1-Very Low, 2- FTPS-Data, FTP-DataTransfer, FTP-Control, FTP Delete Request, FTP Upload Request, FTP Base, Low, 4... All the Allow Authentication FTPS, FTP Download Request Characteristics = Prone Time to misuse, Tra... System Services Technology = Client Server, Netwo... SYSTEM Profiles Category = File Transfer, Hosts and Services Confe... Risk = 3-Medium Administration All the TeamViewer Conferencing, TeamViewer FileTransfer Characteristics = Time Allow Excessive Bandwidth,... Backup & Firmware Technology = Client Server Certificates Save Cancel https://192.168.110.3:4444/webconsole/webpages/index.jsp#71826 1/4 4/1/2017 Sophos Application Application Filter Criteria Schedule Action Applications Log Viewer Facebook Applications, Docstoc Website, Facebook Plugin, MySpace Website, MySpace.cn Website, Twitter Website, Facebook Website, Bebo Website, Classmates Website, LinkedIN Compose Webmail, Digg Web Login, Flickr Website, Flickr Web Upload, Friendfeed Web Login, MONITOR & ANALYZE Hootsuite Web Login, Friendster Web Login, Hi5 Website, Facebook Video -

Examples of Online Social Network Analysis Social Networks
Examples of online social network analysis Social networks • Huge field of research • Data: mostly small samples, surveys • Multiplexity Issue of data mining • Longitudinal data McPherson et al, Annu. Rev. Sociol. (2001) New technologies • Email networks • Cellphone call networks • Real-world interactions • Online networks/ social web NEW (large-scale) DATASETS, longitudinal data New laboratories • Social network properties – homophily – selection vs influence • Triadic closure, preferential attachment • Social balance • Dunbar number • Experiments at large scale... 4 Another social science lab: crowdsourcing, e.g. Amazon Mechanical Turk Text http://experimentalturk.wordpress.com/ New laboratories Caveats: • online links can differ from real social links • population sampling biases? • “big” data does not automatically mean “good” data 7 The social web • social networking sites • blogs + comments + aggregators • community-edited news sites, participatory journalism • content-sharing sites • discussion forums, newsgroups • wikis, Wikipedia • services that allow sharing of bookmarks/favorites • ...and mashups of the above services An example: Dunbar number on twitter Fraction of reciprocated connections as a function of in- degree Gonçalves et al, PLoS One 6, e22656 (2011) Sharing and annotating Examples: • Flickr: sharing of photos • Last.fm: music • aNobii: books • Del.icio.us: social bookmarking • Bibsonomy: publications and bookmarks • … •“Social” networks •“specialized” content-sharing sites •Users expose profiles (content) and links -

Systematic Scoping Review on Social Media Monitoring Methods and Interventions Relating to Vaccine Hesitancy
TECHNICAL REPORT Systematic scoping review on social media monitoring methods and interventions relating to vaccine hesitancy www.ecdc.europa.eu ECDC TECHNICAL REPORT Systematic scoping review on social media monitoring methods and interventions relating to vaccine hesitancy This report was commissioned by the European Centre for Disease Prevention and Control (ECDC) and coordinated by Kate Olsson with the support of Judit Takács. The scoping review was performed by researchers from the Vaccine Confidence Project, at the London School of Hygiene & Tropical Medicine (contract number ECD8894). Authors: Emilie Karafillakis, Clarissa Simas, Sam Martin, Sara Dada, Heidi Larson. Acknowledgements ECDC would like to acknowledge contributions to the project from the expert reviewers: Dan Arthus, University College London; Maged N Kamel Boulos, University of the Highlands and Islands, Sandra Alexiu, GP Association Bucharest and Franklin Apfel and Sabrina Cecconi, World Health Communication Associates. ECDC would also like to acknowledge ECDC colleagues who reviewed and contributed to the document: John Kinsman, Andrea Würz and Marybelle Stryk. Suggested citation: European Centre for Disease Prevention and Control. Systematic scoping review on social media monitoring methods and interventions relating to vaccine hesitancy. Stockholm: ECDC; 2020. Stockholm, February 2020 ISBN 978-92-9498-452-4 doi: 10.2900/260624 Catalogue number TQ-04-20-076-EN-N © European Centre for Disease Prevention and Control, 2020 Reproduction is authorised, provided the -

Perfiles De La Biblioteca En RRSS Y Redes Sociales De Lectura
Red Andaluza de bibliotecas escolares redes sociales Nuevos comportamientos. Uso de RRSS García Guerrero, J. (2012). Entornos para una lectura fomentada. Extracto DR 3 págs. 26-30: https://cutt.ly/DuKE72l AA.VV. (2013). Nuevos comportamientos y formas de leer. Extracto DR 5, págs. 124-143: https://cutt.ly/FuKTgGH AA. VV. (2013). Uso de las redes sociales en la biblioteca escolar. Extracto DR 5: https://cutt.ly/guKTOFU AA.VV. (2013). Gestión de plataformas virtuales para la comunidad de lectores. Extracto DR 5: https://cutt.ly/7uKTZ6s Identidad digital de la biblioteca escolar Olmos Olmos, D. (2016). Gestionar la identidad digital de la biblioteca : https://cutt.ly/cyCDEbR Olmos Olmos, D. (2016). Breve guía de estilo de las publicaciones de la biblioteca escolar: https://cutt.ly/0yCGkUC Red Andaluza de bibliotecas escolares redes sociales Perfiles de la biblioteca en RRSS Twitter. Microblogging en 280 caracteres. Difusión rápida de información destinada especialmente a profesionales, entidades y familias: https://twitter.com Facebook. Red social más utilizada destinada a un amplio abanico de edades. Muy recomendable para dirigirse a familas: https://es-es.facebook.com Pinterest. Tableros para interactuar con usuarios/as y profesionales: https://www.pinterest.es Instagram. Red social más utilizada por el público joven (junto con TiK Tok y Snapchat). Muy recomendable para dirigirse al alumnado: https://www.instagram.com En YouTube está el público. Canal de vídeo. Para difusión de reseñas, actividades, clubes de lectura, proyectos, tutoriales... Lo que recomendable es que la duración del vídeo no sea excesiva: https://www.youtube.com Aplicación de moda entre los más jóvenes. -

Pkn 2012 1.Pdf
TEMATSKI SKLOP Knjiga in ekonomija kulturnih prostorov THEMATIC SECTION The Book and the Economy of Cultural Spaces 1 Marijan Dović, Jernej Habjan, Marko Juvan: Knjiga in ekonomija kulturnih prostorov (predgovor) 5 Marijan Dović, Jernej Habjan, and Marko Juvan: The Book and the Economy of Cultural Spaces (Foreword) 11 Marko Juvan: Kulturni obtok in knjiga: Književnost, vednost, prostor in ekonomija (uvodni zaris) 23 Marko Juvan: Cultural Circulation and the Book: Literature, Knowledge, Space, and Economy (An Introduction) 37 César Domínguez: Circulation in Premodern World Literature: Historical Context, Agency, and Physicality 51 David Šporer: Renaissance Poetry in Print and the Role of Marin Držić 65 Marijana Hameršek: How Did Fairytales Become a Genre of Croatian Children’s Literature? Book History without Books 79 Dragos Jipa: The Literary Canon in the Publishing Apparatus: The Book Series “Les Grands Ecrivains Français” (1887–1913) 91 Jernej Habjan: The Bestseller as the Black Box of Distant Reading: The Case of Sherlock Holmes 107 Alenka Koron: The Private Library of Lojze Kovačič and World Literature 121 Marijan Dović: Economics and Ideologies of the Slovenian Literary Mediation 141 Maja Breznik: The Double Role of the Writer as Worker and Rentier 157 Tiina Aunin: The Book as an Object of the Shared Understanding of Media Changes 165 Jola Škulj: A Challenging Game of Books and the Free Interplay of Cultural Transfer 177 Alexis Weedon: The Book as a Dynamic System for the Commodification of Ideas and Cultural Expressions 189 Miha -

Social Networks Impact on Academic Libraries in Technology Era
Vol. 5(3) Jul-Sep, 2015 ISSN: 2231-4911 Social networks impact on Academic Libraries in Technology Era Dr. Chegoni Ravi Kumar Librarian Government Junior College Mirdoddi-MEDAK, Telangana e-mail: [email protected], [email protected] ABSTRACT This paper deals with concept of social networking and its application to Academic library services for a pro-active awareness and training to educate both the LIS professional and the Teaching Faculty, Students and Research Scholars on the in valuable importance of utilizing social networking in academic library services in digital environment. Keywords: Social Networks, Academic Libraries, Facebook, Twitter, Youtube, Del.icio.us, Digg, MySpace Introduction The changing technology, explosion of information and the transition of academic libraries from print to electronic have influenced the user behavior. Most of the libraries, especially academic libraries are continued to be hybrid (print and electronic) libraries. Compare to other libraries, academic college libraries need special attention in developing collection, systems and services, keeping the hanging-needs and information seeking behavior of the users. The present study has undertaken a survey for assessing the exiting situation, perception and expectations of users in academic college libraries in India. Imagine a time when social network media becomes an integral part of life. In fact, there is no need to imagine anymore, as Facebook and Twitter use soars beyond the combined total of 900 million users. Social network media is -

Reading the Source Code of Social Ties
Reading the Source Code of Social Ties ∗ Luca Maria Aiello Rossano Schifanella Bogdan State Yahoo Labs University of Torino Stanford University Barcelona, Spain Torino, Italy Palo Alto, CA, USA [email protected] [email protected] [email protected] ABSTRACT are usually treated as a priori entities, immediately available to the Though online social network research has exploded during the researcher from the graph of online-mediated interactions such as past years, not much thought has been given to the exploration of emailing, following on Twitter, or friending on Facebook. The so- the nature of social links. Online interactions have been interpreted cial tie is indeed a powerful abstraction that has allowed researchers as indicative of one social process or another (e.g., status exchange to build rigorous models to describe the evolution of social net- or trust), often with little systematic justification regarding the re- works and the dynamics of information exchange [23]. lation between observed data and theoretical concept. Our research Even though previous research on social networks has explored aims to breach this gap in computational social science by propos- the intensity of social links, as well as their polarity [22, 34], there ing an unsupervised, parameter-free method to discover, with high is still much to investigate about the nature of the social interac- accuracy, the fundamental domains of interaction occurring in so- tions implied by social ties. One way to overcome this limitation cial networks. By applying this method on two online datasets dif- is to look into the content of social links, the messages exchanged ferent by scope and type of interaction (aNobii and Flickr) we ob- between actors. -

Crime Prevention in the Virtual Community
CPTED in Bytes The Blurring Lines of Community Barry Davidson Executive Director, ICA Today’s Task Broaden our perspective of the effectiveness of technology in community engagement & crime prevention. Identify technology tools that are current (for the moment) Begin looking forward (Instead of playing catch up!) “Identify the future that has already happened” Peter Drucker Why We Need To Pay Attention Your Corner of The World You Know You Wanted to Know “Old” Tech Tools The Usual Suspects: Email Static Websites Forums/Blogs On-line News Sites The Past The Past We are reactive to social disorder issues Attitude of mistrust of technology by safety professionals More hindsight than foresight: 1994 – Email has no place in the office 1996 – Internet has no place in the office 1998 – eCommerce is too dangerous 2002 – IM is never going catch on 2005 – Social Networking sites are just a fad 2006 - Google maps will not be a usable tool or concern 2008 – YouTube is just a passing fancy for kids Join the Social Networking Revolution The NEW Technology Tools Social Networking Providers: Facebook Facebook Twitter MySpace More than 700 million Nexopia active users Plaxo People spend over Yahoo 700 billion minutes per month on YouTube Facebook RSS Feeds Communications by the thumb . Social Media Stats What is Community? A group of human beings that: have a common interest. common vision. work collaboratively towards a common goal or good. Has no physical or geographic borders Top 4 Social Networking Communities Facebook - Founded by Mark Zuckerberg, Facebook was designed as a social networking site for Harvard students. -

Cloud Computing Bible
Barrie Sosinsky Cloud Computing Bible Published by Wiley Publishing, Inc. 10475 Crosspoint Boulevard Indianapolis, IN 46256 www.wiley.com Copyright © 2011 by Wiley Publishing, Inc., Indianapolis, Indiana Published by Wiley Publishing, Inc., Indianapolis, Indiana Published simultaneously in Canada ISBN: 978-0-470-90356-8 Manufactured in the United States of America 10 9 8 7 6 5 4 3 2 1 No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, 201-748-6011, fax 201-748-6008, or online at http://www.wiley.com/go/permissions. Limit of Liability/Disclaimer of Warranty: The publisher and the author make no representations or warranties with respect to the accuracy or completeness of the contents of this work and specifically disclaim all warranties, including without limitation warranties of fitness for a particular purpose. No warranty may be created or extended by sales or promotional materials. The advice and strategies contained herein may not be suitable for every situation. This work is sold with the understanding that the publisher is not engaged in rendering legal, accounting, or other professional services. -

Manuale Anobii
ANOBII PER LE BIBLIOTECHE MANUALE DUSO A cura dei Tirocinanti PICA Progetto: La Biblioteca? Mi Piace! Manuale d’uso ANOBII PER LE BIBLIOTECHE INTRODUZIONE Questo manuale duso del social network aNobii è destinato al personale bibliotecario per estendere linterazione tra beni librari e lutenza potenzialmente interessata allargomento. Per meglio fidelizzare i diretti interessati alluso della biblioteca intesa come sede fisica, è dobbligo, oggi, riferirsi a contesti virtuali specifici per ampliare i servizi garantendo risultati ottimali riferiti alle fasce di utenza più giovani. INDICE 1.1.1. Creazione di un profilo su aNobii p. 2 2.2.2. Primi passi p. 3 3.3.3. Caricamento di un nuovo libro sullo scaffale p. 5 4.4.4. Visualizzazione della scheda di un libro p. 7 5.5.5. Creazione di una libreria personalizzata p. 11 6.6.6. La pagina della libreria personale p. 16 7.7.7. Gestione dei tag p. 20 8.8.8. Impostazioni e informazioni personali p. 23 9.9.9. Esportazione della libreria p. 26 10.10.10. Scegliere e seguire i gruppi p. 30 11.11.11. Aggiungere amici e vicini p. 33 APPENDICE: Lesperienza su aNobii del progetto PiCA La Biblioteca? Mi piace! p. 36 Pagina | 1 Manuale d’uso ANOBII PER LE BIBLIOTECHE 1. CREAZIONE DI UN PROFILO SU ANOBII ⇒⇒⇒ Digitando http://www.anobii.com si entra nella Home Page di aNobii. ⇒⇒⇒ Cliccare su IscrivitiIscrivitiIscriviti in alto a destra per accedere alla pagina della registrazione; inserire email e password e cliccare poi sul pulsante azzurro IscrivitiIscrivitiIscriviti.... Pagina | 2 Manuale d’uso ANOBII PER LE BIBLIOTECHE ⇒⇒⇒ Verrà richiesto l'inserimento di due parole mascherate per dimostrare di non essere un sistema automatizzato (che potrebbe essere utilizzato per inviare spam“. -

The Impact of the Internet and Digitalization on the European
April 2017 The impact of the internet and digitalization on the European creative sector by Oliver & Ohlbaum Associates Ltd and Analysys Mason About Oliver & Ohlbaum Oliver & Ohlbaum (O&O) is one of Europe’s leading independent policy and strategy advisors to the media and entertainment industry, where it has unrivalled knowledge and expertise. O&O’s clients include leaders in digital media, digital streaming services and several European television stations. About Analysys Mason Analysys Mason is an international consultancy renowned for its expertise, independence and rigour in the telecoms, media and technology sectors. Its portfolio includes multiple projects on the long-term evolution of TV distribution platforms and work for regulators on the use of data in the media and online publishing sectors. This report was written by Oliver & Ohlbaum Associates Ltd and Analysys Mason, and was commissioned and funded by Google. The opinions stated therein are those of the authors. Every effort has been made to trace copyright holders and obtain permission for the use of such material in this report. The authors apologise for any errors or omissions, and ask that they be notified of any corrections. THE IMPACT OF THE INTERNET ON THE CREATIVE SECTOR Contents Glossary 4 Key facts 6 Summary 7 1 Introduction 13 1.1 Background 13 1.2 Scope 13 1.3 Methodology 14 2 The creative industries 17 2.1 Our definition of the creative industries 17 2.1.1 Four core creative industries and cultural institutions 17 2.1.2 Our definition depends on available data -

Friendship Prediction and Homophily in Social Media Luca Maria Aiello, Alain Barrat, Rossano Schifanella, C
Friendship prediction and homophily in social media Luca Maria Aiello, Alain Barrat, Rossano Schifanella, C. Cattuto, Benjamin Markines, Filippo Menczer To cite this version: Luca Maria Aiello, Alain Barrat, Rossano Schifanella, C. Cattuto, Benjamin Markines, et al.. Friend- ship prediction and homophily in social media. ACM Transactions on the Web, http://tweb.acm.org/, 2012, 6 (2), pp.9. 10.1145/2180861.2180866. hal-00718085 HAL Id: hal-00718085 https://hal.archives-ouvertes.fr/hal-00718085 Submitted on 16 Jul 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Friendship prediction and homophily in social media LUCA MARIA AIELLO Department of Computer Science, University of Turin, Italy ALAIN BARRAT Centre de Physique Th´eorique (CNRS UMR 6207), Marseille, France Complex Networks and Systems Laboratory, ISI Foundation, Turin, Italy ROSSANO SCHIFANELLA Department of Computer Science, University of Turin, Italy CIRO CATTUTO Complex Networks and Systems Laboratory, ISI Foundation, Turin, Italy BENJAMIN MARKINES FILIPPO MENCZER School of Informatics and Computing, Indiana University, Bloomington, IN, USA Web 2.0 applications have attracted considerable attention because their open-ended nature allows users to create lightweight semantic scaffolding to organize and share content.