DOCSLIB.ORG

Multiwinner Analogues of the Plurality Rule: Axiomatic and Algorithmic Perspectives

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Multiwinner Analogues of the Plurality Rule: Axiomatic and Algorithmic Perspectives Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16) Multiwinner Analogues of the Plurality Rule: Axiomatic and Algorithmic Perspectives Piotr Faliszewski Piotr Skowron Arkadii Slinko Nimrod Talmon AGH University University of Oxford University of Auckland TU Berlin Krakow, Poland Oxford, United Kingdom Auckland, New Zealand Berlin, Germany [email protected] [email protected] [email protected] [email protected] Abstract most desired one to the least desired one, and the goal is to pick a committee of a given size k that, in some sense, best We characterize the class of committee scoring rules that sat- matches the voters’ preferences. Naturally, the exact mean- isfy the fixed-majority criterion. In some sense, the commit- ing of the phrase “best matches” depends strongly on the ap- tee scoring rules in this class are multiwinner analogues of the single-winner Plurality rule, which is uniquely character- plication at hand, as well as on the societal conventions and ized as the only single-winner scoring rule that satisfies the understanding of fairness. For example, if we are to choose simple majority criterion. We find that, for most of the rules a size-k parliament, then it is important to guarantee pro- in our new class, the complexity of winner determination is portional representation; if the goal is to pick a group of high (i.e., the problem of computing the winners is NP-hard), products to offer to customers, then it might be important to but we also show some examples of polynomial-time winner maintain diversity of the offer; if we are to shortlist a group determination procedures, exact and approximate. of candidates for a job, then it is important to focus on the quality of the selected candidates regardless of how similar Introduction some of them might be. In effect, there is quite a variety of multiwinner voting The scoring rules in general, and the Plurality rule specifi- rules. For example, under the SNTV rule, the winning com- cally, are among the most basic and the best studied single- mittee consists of k candidates who are ranked first more winner voting rules. However, our understanding of their frequently than others. Under the Bloc rule, each voter gives recently-introduced multiwinner analogues, committee scor- one point to each candidate he or she ranks among his or ing rules (Elkind et al. 2014), is very limited. In this paper, her top k positions, and the committee consists of k candi- we attempt to rectify this situation by asking a seemingly dates with the most points. Under the Chamberlin–Courant very innocuous question: what is the committee scoring rule rule, the winning committee consists of k candidates such analogue of the Plurality rule? Using an axiomatic approach, that each voter ranks his or her most preferred committee we find a rather surprising answer. Not only is there a whole member as high as possible (for the exact definition see the class of committee scoring rules that correspond to the Plu- original paper of Chamberlin and Courant (1983) or pa- rality rule, but also one of the most natural candidates to be pers studying the rule’s features and computational com- the multiwinner Plurality, the single non-transferable vote plexity (Procaccia, Rosenschein, and Zohar 2008; Lu and rule (the SNTV rule), falls short on our criterion. On the Boutilier 2011; Elkind et al. 2014; Skowron, Faliszewski, other hand, the Bloc rule turns out to be quite a satisfy- and Slinko 2015; Skowron and Faliszewski 2015)). ing candidate, but certainly not the only one. In addition to The three rules mentioned above are examples of commit- our axiomatic study, we provide an algorithmic analysis of tee scoring rules (a class of rules generalizing single-winner this new class of committee scoring rules. In particular, we scoring rules to the multiwinner setting, recently introduced show that it can be seen as a subfamily of the OWA-based by Elkind et al. (2014); see the preliminaries for the defini- rules of Skowron, Faliszewski, and Lang (2015) (also stud- tion).1 Of course, there are natural multiwinner rules that ied by Aziz et al. (2015b; 2015a); see also the work of Kil- cannot be expressed as committee scoring rules, such as gour (2010) for a more general overview of approval-based the single transferable vote rule (the STV rule), the Mon- multiwinner rules). However, the hardness results for gen- roe rule (Monroe 1995), or all the multiwinner rules based eral OWA rules do not translate directly to our case (and on the Condorcet principle (see, e.g., the works of Elkind et some indeed do not even hold). On the side, we provide an al. (2011), Fishburn (1981), and Gehrlein (1985)). Nonethe- axiomatic characterization of the Bloc rule (among the com- less, we believe that committee scoring rules form a very mittee scoring rules). diverse class of voting rules that deserves a further study. Let us now describe our setting more precisely. In a mul- We ask for a committee scoring rule that can be seen as tiwinner election, each voter ranks the candidates from the Copyright c 2016, Association for the Advancement of Artificial 1Naturally, these rules were known much earlier than Elkind et Intelligence (www.aaai.org). All rights reserved. al. (2014) introduced the unifying framework for them. 482 a “multiwinner analogue” of the Plurality rule. Intuitively, it of voters. The number m = |C| will be fixed throughout the might seem as if the SNTV rule were such a rule and the paper. Each voter vi is associated with a preference order i question were trivial. However, instead of following this in- in which vi ranks the candidates from its most desirable one tuition we take an axiomatic approach. We note that Plural- to its least desirable one. If X and Y are two (disjoint) sub- ity is the only single-winner scoring rule that has the simple sets of C, then by X i Y we mean that for each x ∈ X majority property, i.e., that guarantees that if a candidate is and each y ∈ Y it holds that x i y. For a positive integer t, ranked first by a simple majority of the voters, then he or she we denote the set {1,...,t} by [t]. is the unique winner of the election. We ask for a committee scoring rule that has the fixed-majority criterion (a multi- Single-Winner Voting Rules. A single-winner voting winner analogue of the simple majority property, introduced rule R is a function that, given an election E =(C, V ), by Debord (1993)), which requires that if there is a majority outputs a subset of those candidates that tie as winners. of voters each of whom ranks the same k candidates in the There is quite a variety of single-winner voting rules, but top k positions (perhaps in a different order), then these k in this paper it suffices to consider the scoring rules. Given candidates should form a unique winning committee. a voter v and a candidate c, we write posv(c) to denote the The Bloc rule obviously satisfies the fixed-majority crite- position of c in v’s preference order (e.g., if v ranks c first rion. However, it turns out that Bloc is by far not the only then posv(c)=1). A scoring function for m candidates is such committee scoring rule and there is a whole family of a function γ :[m] → N such that for each i ∈ [m − 1] we them. We provide an (almost) full characterization of this have γ(i) ≥ γ(i +1). Each scoring function γ defines a family2 and analyze the computational complexity of win- voting rule Rγ as follows. Let E =(C, V ) be an election 3 ner determination for rules in this family. Initially, we iden- with m candidates.Under Rγ , each candidate c ∈ C re- tify a slightly larger class of top-k-counting rules for which ceives score(c):= v∈V γ(posv(c)) points and the candi- the score that a committee receives from a given voter is a date with the highest number of points wins. (If there are function of the number of committee members that this voter several such candidates, then they all tie as winners; this ranks in the top k positions of its vote; we refer to this func- view is known as the nonunique-winner model.) We often tion as the counting function. We obtain the following main refer to the value score(c) as the γ-score of c. results: The following scoring functions are particularly interest- t αt(i)=1 1. For a large class of counting functions, top-k-counting ing. The -approval scoring function is defined as i ≤ t αt(i)=0 rules are NP-hard to compute. There are, however, some for and otherwise. For example, the Plurality rule is Rα , the t-Approval rule is Rα , and the polynomial-time computable ones (e.g., the Bloc rule and 1 t Veto rule is Rα (where m is the number of candidates). the Perfectionist rule that we introduce). m−1 The Borda scoring function for m candidates is defined as 2. If the counting function is convex, then the top-k-counting βm(i):=m − i, and Rβ is the Borda rule. rule that it defines satisfies the fixed-majority criterion (for a fairly intuitive relaxation of the convexity notion Multiwinner Voting Rules. A multiwinner voting rule R we get an “if and only if” result). is a function that, given an election E =(C, V ) and a num- k 3.
Load more

Recommended publications
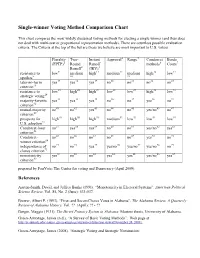
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
  • Minimax Is the Best Electoral System After All
    1 Minimax Is the Best Electoral System After All Richard B. Darlington Department of Psychology, Cornell University Abstract When each voter rates or ranks several candidates for a single office, a strong Condorcet winner (SCW) is one who beats all others in two-way races. Among 21 electoral systems examined, 18 will sometimes make candidate X the winner even if thousands of voters would need to change their votes to make X a SCW while another candidate Y could become a SCW with only one such change. Analysis supports the intuitive conclusion that these 18 systems are unacceptable. The well-known minimax system survives this test. It fails 10 others, but there are good reasons to ignore all 10. Minimax-T adds a new tie-breaker. It surpasses competing systems on a combination of simplicity, transparency, voter privacy, input flexibility, resistance to strategic voting, and rarity of ties. It allows write-ins, machine counting except for write-ins, voters who don’t rate or rank every candidate, and tied ratings or ranks. Eleven computer simulation studies used 6 different definitions (one at a time) of the “best” candidate, and found that minimax-T always soundly beat all other tested systems at picking that candidate. A new maximum-likelihood electoral system named CMO is the theoretically optimum system under reasonable conditions, but is too complex for use in real-world elections. In computer simulations, minimax and minimax-T nearly always pick the same winners as CMO. Comments invited [email protected] Copyright Richard B. Darlington May be distributed free for non-commercial purposes 2 1.
    [Show full text]
  • Arxiv:1811.06739V3 [Cs.GT] 3 Jun 2019 St
    MEASURING MAJORITY POWER AND VETO POWER OF VOTING RULES ALEKSEI Y. KONDRATEV AND ALEXANDER S. NESTEROV Abstract. We study voting rules with respect to how they allow or limit a majority from dominating minorities: whether a voting rule makes a majority powerful, and whether minorities can veto the candidates they do not prefer. For a given voting rule, the minimal share of voters that guarantees a victory to one of their most preferred candidates is the measure of majority power, and the minimal share of voters that allows them to veto each of their least preferred candidates is the measure of veto power. We find tight bounds on these minimal shares for voting rules that are popular in the literature and in real elections. We order these rules according to majority power and veto power. The instant-runoff voting has both the highest majority power and the highest veto power and the plurality rule has the lowest. In general, the higher the majority power of a voting rule is, the higher its veto power. The three exceptions are: voting with proportional veto power, Black’s rule, and Borda rule, which have a relatively low level of majority power and a high level of veto power and thus provide minority protection. Our results can shed light on how voting rules provide different incentives for voter participation and candidate nomination. Keywords: majority tyranny, voting system, plurality voting, two-round system, Borda count, voting paradox, minority protection, electoral participation, voting procedure, voting method, voting rule, preferential voting, electoral system JEL Classification D71, D72 Date: 03 June 2019.
    [Show full text]
  • Voting Criteria
    Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether voting methods are doing their jobs; that is, the criteria we use to determine if a voting system is reasonable and fair. We use all notation as in the previous set of notes. 1. Majority Criterion: If a candidate gets > 50% of the first place votes, that candidate should be the winner. This criterion is quite straightforward. If a candidate is preferred by more than half of the voters, this candidate by all rights should win the election. No other candidate could be more satisfactory for more people than the first choice of more than 50% of the voters. It is immediately obvious that the plurality method and the runoff methods will satisfy this criterion, since their method of determining the winner is fundamentally based on first place votes. For other methods, the criterion is less clear. 2. Condorcet Criterion: If a candidate wins every pairwise comparison, then that candidate should be the winner. This should remind you of the Condorcet method for choosing a winner. Of course, it is immediately obvious that if the Condorcet method produces a winner without having to resolve ties, then that candidate wins the election in that method, so clearly the Condorcet method satisfies the Condorcet criterion. However, it is not clear that the other methods will satisfy this criterion; for example, in Hare method, is it possible to eliminate a candidate that would otherwise be a Condorcet winner? 3.
    [Show full text]
  • Voting and Apportionment 14.3 Apportionment Methods 14.4 Apportionment One of the Most Precious Rights in Our Democracy Is the Right to Vote
    304470-ch14_pV1-V59 11/7/06 10:01 AM Page 1 CHAPTER 14 The concept of apportionment or fair division plays a vital role in the operation of corporations, politics, and educational institutions. For example, colleges and universities deal with large issues of apportionment such as the allocation of funds. In Section 14.3, you will encounter many different types of apportionment problems. David Butow/Corbis SABA 14.1 Voting Systems* 14.2 Voting Objections Voting and Apportionment 14.3 Apportionment Methods 14.4 Apportionment One of the most precious rights in our democracy is the right to vote. Objections We have elections to select the president of the United States, senators and representatives, members of the United Nations General Assembly, baseball players to be inducted into the Baseball Hall of Fame, and even “best” performers to receive Oscar and Grammy awards. There are many *Portions of this section were developed by ways of making the final decision in these elections, some simple, some Professor William Webb of Washington more complex. State University and funded by a National Electing senators and governors is simple: Have some primary elec- Science Foundation grant (DUE-9950436) tions and then a final election. The candidate with the most votes in the awarded to Professor V. S. Manoranjan. final election wins. Elections for president, as attested by the controver- sial 2000 presidential election, are complicated by our Electoral College system. Under this system, each state is allocated a number of electors selected by their political parties and equal to the number of its U.S.
    [Show full text]
  • Fairness Criteria Voting Methods
    VOTING METHODS FAIRNESS CRITERIA Majority Criterion – If a candidate wins by a Majority – receiving more than half of the first majority, then that candidate should win the place votes election by another method. Evaluation – If the majority winner does not win by another Plurality Method – receiving the most first place method, then this criterion is violated. If votes majority winner does win by another method, then it is not violated. Plurality with Elimination – Check first place votes for a majority. If candidate has a majority, then Head-to-head Criterion – If a candidate wins by declared winner. If not, eliminate the candidate head-to-head (pairwise) over every other with the fewest first place votes and recount. candidate, then that candidate should win the Recount. Continue until a candidate wins by a election. Evaluation – If one candidate wins over majority. all others when paired up and does not win by another method, then the criterion is violated. If Borda Count Method – Voters rank candidates on by another method, the head-to-head winner ballot. Assign 1 point to last place, 2 points to next, still wins, then the criterion is not violated. etc. Total points for each candidate. Candidate with the most points wins. Irrelevant Alternatives Criterion – A candidate wins. In a recount the only changes are that one Pairwise Comparison (Head-to-Head) Method – or more of the candidates are removed. Original Voters rank candidates on ballot. Pair up winner should win. Evaluation – A candidate candidates so each is compared with every other. drops out. Look at the 1st place votes.
    [Show full text]
  • Multiwinner Analogues of the Plurality Rule: Axiomatic and Algorithmic Perspectives
    Soc Choice Welf https://doi.org/10.1007/s00355-018-1126-4 ORIGINAL PAPER Multiwinner analogues of the plurality rule: axiomatic and algorithmic perspectives Piotr Faliszewski1 · Piotr Skowron2 · Arkadii Slinko3 · Nimrod Talmon4 Received: 12 September 2017 / Accepted: 9 April 2018 © The Author(s) 2018 Abstract We characterize the class of committee scoring rules that satisfy the fixed- majority criterion. We argue that rules in this class are multiwinner analogues of the single-winner Plurality rule, which is uniquely characterized as the only single-winner scoring rule that satisfies the simple majority criterion. We define top-k-counting committee scoring rules and show that the fixed-majority consistent rules are a subclass of the top-k-counting rules. We give necessary and sufficient conditions for a top-k- counting rule to satisfy the fixed-majority criterion. We show that, for many top-k- counting rules, the complexity of winner determination is high (formally, we show that the problem of deciding if there exists a committee with at least a given score is NP- hard), but we also show examples of rules with polynomial-time winner determination procedures. For some of the computationally hard rules, we provide either exact FPT algorithms or approximate polynomial-time algorithms. A preliminary version of this paper was presented at AAAI-2016 (Faliszewski et al. 2016). Nimrod Talmon: Most of the work was done while the author was affiliated with TU Berlin (Berlin, Germany) and Weizmann Institute of Science (Rehovot, Israel). B Piotr Skowron [email protected] 1 AGH University, Kraków, Poland 2 University of Warsaw, Warsaw, Poland 3 University of Auckland, Auckland, New Zealand 4 Ben-Gurion University of the Negev, Be’er Sheva, Israel 123 P.
    [Show full text]
  • Weak Mutual Majority Criterion for Voting Rules
    Weak Mutual Majority Criterion for Voting Rules Aleksei Yu. Kondratev1 and Alexander S. Nesterov2 1 Higher School of Economics, Kantemirovskaya 3, 194100 St.Petersburg, Russia [email protected] 2 Higher School of Economics, Kantemirovskaya 3, 194100 St.Petersburg, Russia [email protected] Abstract We study a novel axiom for voting rules: the weak mutual majority criterion (WMM). A voting rule satisfies WMM if whenever some k candidates receive top k ranks from a qualified majority that consists of more than q = k=(k+1) of voters, the rule selects the winner among these k candidates. WMM lies between the two standard axioms: it is stronger than the majority criterion (here k = 1 and q = 1=2) and weaker than the mutual majority criterion (MM, here for any k the size of majority is fixed q = 1=2). The widespread plurality rule satisfies WMM (but not MM). Moreover, for any k the bound q = k=(k + 1) is tight. The plurality with runoff rule, the Dodgson's rule, the Condorcet least reversal rule, the Simpson's rule, and the Young's rule satisfy WMM, for most of these rules we also find tight bounds on the size of the qualified majority q. The well-known Black's rule and its positional version do not satisfy WMM: for k > 1 its tight bound q = 1. We propose two modifications of the Black's positional rule that satisfy WMM: the qualified mutual majority rule with the tight bound q = k=(k + 1) and the convex median voting rule with the tight bound q = (3k − 1)=(4k).
    [Show full text]
  • Math 017 Lecture Notes
    Math 017 Lecture Notes (1.1) Preference Ballots and Schedules Election ingredients: - Set of choices/candidates to choose from - Voters whom make these choices - Ballots lets voters designate their choices (vote on something): ski/snowboard/other (both ways) - Say we only ask for one of the three choices. Define Linear Ballot - We can also design ballots that rank the choices in order of most to least preferable (define Preference Ballot) - Naturally, since there are a limited number of choices for ranking these choices, we can organize ballots by their respective rankings. Define Preference Ballot (draw it) Link this vocabulary to the vote: Preference ballot: voters are asked to rank candidates/choices Linear Ballot: plain vote (disregard lesser choice candidates) Preference Schedule: organize matching ballots Transitivity of Elimination Candidates: preferring choices A over B and B over C implies A is preferred over C o This implies relative preference of a voter is not affected by the elimination of candidate(s) o Eg. Eliminate one of the activities we’ve voted on, show new schedule (1.2) The Plurality Method Plurality Method: Only choose first place votes (most votes wins = plurality candidate) Principle of Majority Rule: In an election with 2 candidates, the candidate with the more than half the votes wins (majority candidate). Harder to accomplish when more than 2 candidates. Plurality candidate not necessarily a majority candidate Democratic Criteria Majority Criterion: If candidate X has majority (>half!) of first-place votes than X should win the election - Majority => plurality but plurality ≠> majority! - Let m = # of votes for majority, then if N = total number of votes, then m = ceil(N/2 +1) - If a majority candidate does not win the election we say the Majority Criterion has been violated (e.g.
    [Show full text]
  • Fairness Criteria
    There is no consistently fair way to choose the winner of an election. A voting method that is democratic and always fair is a mathematical impossibility. Arrow's Impossibility Theorem Kenneth Arrow 1952 Fairness Criteria The Fairness Criteria are things that should always be true according to common sense, but aren't always true in reality. Majority Criterion Book : If there is a choice that has a majority of the first-place votes in an election, then that choice should be the winner of the election. Translation : If someone gets the majority of the votes, then they should win. Condorcet Criterion Book : If there is a choice that in a head-to-head comparison is preferred by the voters over every other choice, then that choice should be the winner of the election. Translation : If Bob is preferred over Jon in a one-on-one comparison and Bob is preferred over Stacey and Bob is preferred over Shelley, then Bob should win the election. Monotonicity Criterion Book : If choice X is a winner of an election and, in a reelection, the only changes in the ballots are changes that only favor X, then X should remain a winner of the election. Translation : Bob wins an election. For some reason there is a reelection. Some people change their minds and rank Bob higher in their preference ballots. Bob should still win the election. Independence of Irrelevant Alternatives Criterion Book : If candidate or alternative X is a winner of an election and one (or more) of the other candidates or alternatives is removed and the ballots recounted, then X should still be a winner of the election.
    [Show full text]
  • Liberal Democrats
    Liberal Democrats From Wikipedia, the free encyclopedia This article is about the British political party. For similarly named parties in other countries, see Liberal Democratic Party. For the system of government, see Liberal democracy. Liberal Democrats Leader Nick Clegg MP Deputy Leader Simon Hughes MP President Tim Farron[1] MP Founded 2 March 1988 Merger of Liberal Party and SDP Preceded by SDP-Liberal Alliance 8-10 Great George Street, Headquarters London, SW1P 3AE [2] Youth wing Liberal Youth Membership (2010) 65,038[3] Liberalism Social liberalism Cultural liberalism Economic liberalism[4] Internal ideological trends: Ideology • Green politics • Green Liberalism • Civil libertarianism • Internationalism[5] • Social democracy • Community politics[6] Radical centre to Centre- Political position left[7][8][9] International Liberal International affiliation European Liberal Democrat European affiliation and Reform Party European Alliance of Liberals and Parliament Group Democrats for Europe [10] Official colours Yellow 57 / 650 House of Commons [11] 79 / 738 House of Lords [12][13] European 12 / 72 [14] Parliament London Assembly 3 / 25 Scottish Parliament 5 / 129 5 / 60 Welsh Assembly [15][16] 3,078 / 21,871 Local government [17] Website libdems.org.uk Politics of the United Kingdom Political parties Elections The Liberal Democrats are a social liberal political party in the United Kingdom which supports constitutional and electoral reform,[18] progressive taxation,[19] wealth taxation,[20] human rights laws,[21] cultural liberalism,[22] banking reform[23] and civil liberties (the party president's book of office is John Stuart Mill's 1859 On Liberty). The party was formed in 1988 by a merger of the Liberal Party and the Social Democratic Party.
    [Show full text]
  • Mathematics and Social Choice Theory Topic 4 – Voting Methods
    Mathematics and Social Choice Theory Topic 4 { Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow's Impossibility Theorem 4.4 Cumulative voting and proportional representation 4.5 Fair majority voting - eliminate Gerrymandering 1 4.1 Social choice procedures • A group of voters are collectively trying to choose among several al- ternatives, with the social choice (the \winner") being the alternative receiving the most votes (based on a specified voting method). • How to take in the information of individual comparisons among the alternatives in the determination of the winner? • What are the intuitive criteria to judge whether a social choice is \reasonably" acceptable? Is the choice the least unpopular, broadly acceptable, winning in all one-for-one contests, etc? 2 Example 3 candidates are running for the Senate. By some means, we gather the information on the \preference order" of the voters. 22% 23% 15% 29% 7% 4% DDHHJJ HJDJHD JHJDDH Topchoice only 45% for D, 44% forHJ and 11% for ; D emerges as the "close'" winner. One-for-one contest H scores (15 + 29 + 7)% = 51% betweenHDD and scores (22 + 23 + 4)% = 49%. 3 General framework Set A whose elements are called alternatives (or candidates); a; b; c, etc. Set P whose elements are called people (or voters); p1; p2; p3, etc. • Each person p in P has arranged the alternatives in a list according to his preference. • A social choice procedure is a fixed \receipt" for choosing an alter- native based on the preference orderings of the individuals.
    [Show full text]