A Short Survey of N Etwork Economics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Children and the Economics of Christmas Gift-Giving
Applied Economics Letters, 1995, 2, 295–297 Children and the economics of Christmas gift-giving CAR OL HORT ON T RE M B L AY* and VIC T OR J. T R E M BL AY * Oregon State University, Department of Economics, Ballard Extension Hall 303, Corvallis, OR 97331-3612, USA Received 22 March 1995 In spite of its importance to the retail sector, there has been relatively little research on the economics of Christmas Season gift-giving. The one exception is Waldfogel (1993), The Deadweight loss of Christmas, American Economic Review, 83, 1328–1336, who found a substantial amount of deadweight loss associated with Christmas gift-giving. Here it is shown that the Waldfogel study is incomplete and alternative models of consumer choice theory which better explain Christmas gift-giving are identified. Although the standard neoclassical and altruistic models predict no relationship between the population of children and per capita Christmas spending, a model is developed that includes non-pecuniary externalities and predicts that children have a positive impact on Christmas gift-giving. This prediction is supported by empirical evidence. I. I NT R ODUC T ION II . T HE E C ONOM IC S OF GI F T- GI VIN G Holiday or Christmas season gift-giving is very important to The economics of gift-giving is rather elementary in the neoclassical the retail sector of the economy.1 For example, US retailers world found in most intermediate textbooks. In this setting, normally generate 25% of sales and 60% of profits between consumer preferences are represented by an increasing, twice Thanksgiving and New Year’s Day (Fortune, 1985; Business continuously differentiable, and strictly concave utility function, Week, 1993). -

An Ethnohistorical Review of Health and Healing in Aklavik, NWT, Canada
“Never Say Die”: An Ethnohistorical Review of Health and Healing in Aklavik, NWT, Canada by Elizabeth Cooper A Thesis submitted to the Faculty of Graduate Studies of The University of Manitoba in partial fulfilment of the requirements of the degree of MASTER OF ARTS Department of Native Studies University of Manitoba Winnipeg Copyright © 2010 by Elizabeth Cooper Abstract The community of Aklavik, North West Territories, was known as the “Gateway to the North” throughout the first half of the Twentieth Century. In 1959, the Canadian Federal Government decided to relocate the town to a new location for a variety of economic and environmental reasons. Gwitch’in and Inuvialuit refused to move, thus claiming their current community motto “Never Say Die”. Through a series of interviews and participant observation with Elders in Aklavik and Inuvik, along with consultation of secondary literature and archival sources, this thesis examines ideas of the impact of mission hospitals, notions of health, wellness and community through an analysis of some of the events that transpired during this interesting period of history. Acknowledgements I would like to thank and honour the people in both Aklavik and Inuvik for their help and support with this project. I would like to thank my thesis committee, Dr. Christopher G Trott, Dr Emma LaRocque and Dr. Mark Rumel for their continued help and support throughout this project. I would like to thank the Social Sciences and Humanities Research Council, Dr. S. Michelle Driedger’s Research in Science Communication CIHR-CFI Research Lab, University of Manitoba Graduate Studies, University of Manitoba Faculty of Arts, University of Manitoba, Department of Native Studies and University of Manitoba Graduate Students Association, for making both the research and dissemination of results for this project possible. -

Fall 2009 Fall 2009 Fall Non-Profit Org
41 William Street, Princeton, New Jersey 08540-5237 Fall 2009 Fall 2009 NON-PROFIT ORG. U.S. POSTAGE 41 William Street, Princeton, New Jersey 08540-5237 PAID HAMMOND, IN PERMIT #197 Fall 2009 Fall 2009 Princeton University Press Princeton University Press Information for Booksellers Information for Individuals C ONTENTS A LETTER FROM THE DIRECTOR c/o California / Princeton Domestic discount codes are: New Jersey residents include 7% sales n TRADE 1 Fulfillment Services, Inc. T=Trade; S=Short; J=Special series; tax. California residents include 9.25% A great editor once said that good publishing is always about 1445 Lower Ferry Road X=Text sales tax. Canadian customers add n NATURAL HISTORY 28 something. At Princeton, what we’re about is meeting the challenge Ewing, NJ 08618 5% GST. For mail order, individuals n PRINCETON REFERENCE 35 of creating a list with a singular personality, while drawing books Agency Plan must include payment in cash, check, Toll-Free Order Line Princeton University Press also offers or money order, or charge to Visa or n ACADEMIC TRADE 36 from fields as different and divergent as applied mathematics, clas- (U.S. & Canada only) a preferred discount plan to book- MasterCard. Include $4 postage for n PAPERBACKS 51 sics, natural history, and financial economics. We seek to publish a 1 (800) 777 4726 stores that meet minimum stocking the first book and $1 for each n LITERATURE 71 list that, as John Henry Newman described the work of education, Monday through Friday requirements. For details, contact your additional book. “takes a connected view of old and new, past and present, far and 8 A.M.–7:30 P.M. -

Economic and Market Overview
DECEMBER 2020 ECONOMIC AND MARKET OVERVIEW Global After all the hype around the 3 November US election, interest in US politics has died away surprisingly quickly as it became apparent that Joe Biden will most likely be inaugurated on 20 January 2021. This change in news focus was perhaps not all that surprising as more relevant matters, such as a second Covid-19 wave in the northern hemisphere and accompanying lockdowns, are threatening to derail the global economic recovery. Various vaccines seem to be in the final stage of approval, but distribution of these and the willingness of communities to be vaccinated also play a role in creating the conditions for a sustained return to previous levels of economic activity. This is clear from a recent report published by TS Lombard, an independent economic and investment strategy research house. They concluded that the world economy will benefit from an effective vaccine (or vaccines) but that it also faces two major downside developments: the second wave of infections which is more virulent than previously expected (especially in Europe), and delays in the implementation of a second fiscal stimulus package in the United States which was originally scheduled for the end of the third quarter this year. They believe that the vaccine upside and these short-term downsides should combine to sustain stock markets at their current very high ratings: the downsides and resulting disappointing Q4 and Q1 growth will keep central bank policies ultra-easy, while the prospective consumption benefits from the vaccine will sustain investor confidence. The “risk-on” sentiment among investors put further pressure on the US Dollar with emerging markets The “risk-on” currencies being the major beneficiaries of capital flows. -

Belief and Christmas: Performing Belief and the Theory and Practice of Christmas Performance
University of Central Florida STARS Electronic Theses and Dissertations, 2004-2019 2013 Belief And Christmas: Performing Belief And The Theory And Practice Of Christmas Performance Brenna Nicely University of Central Florida Part of the Theatre and Performance Studies Commons Find similar works at: https://stars.library.ucf.edu/etd University of Central Florida Libraries http://library.ucf.edu This Masters Thesis (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Electronic Theses and Dissertations, 2004-2019 by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Nicely, Brenna, "Belief And Christmas: Performing Belief And The Theory And Practice Of Christmas Performance" (2013). Electronic Theses and Dissertations, 2004-2019. 2817. https://stars.library.ucf.edu/etd/2817 BELIEF AND CHRISTMAS PERFORMING BELIEF AND THE THEORY AND PRACTICE OF CHRISTMAS PERFORMANCE by BRENNA NICELY B.A. Bowdoin College, 2010 A thesis submitted in partial fulfillment of the requirements for the degree of Master of Arts in the Department of Theatre in the College of Arts and Humanities at the University of Central Florida Orlando, Florida Spring Term 2013 Major Professor: Julia Listengarten © 2013 Brenna Nicely ii ABSTRACT In the United States, Christmastime has become a time of tension between the holy ideals of family togetherness, childhood innocence, and goodwill towards men and commercial idolatry. Christ and Santa Claus are pitted against each other in the war on Christmas between religion and secularism instead of feasting together on ham and figgy pudding in the traditional fashion. -

December 2015.Pub
O P C News from the Crossroads December 2015 Overbrook Presbyterian Church Mall Time Is Christmas Time would be a true blessing if the is a welcoming and diverse intended spirit of Christmas did last Chrisan community that seeks I was at the Willow Grove Mall a the year through. It is a poignant acvely to love and serve God, month ago or so, which was at the irony that the merchants of our world each other, and the world. me over a full week before are doing a beer job of extending —Mission Statement Halloween. I went there to pick up a their Christmas season than are the spatula or something for the kitchen believers who call themselves Overbrook Church Staff and to get a hands‐free earpiece for Chrisans. Merchants are busily at Rev. Dr. Andrew H. Mann, Jr. my cell phone. As I walked from the work extending the season; believers Interim Minister parking lot into the mall, I entered pull Christmas out of the ac boxes Rev. David K. McMillan through Bloomingdale’s. My mind later and later and rush them away Pastor Emeritus was off somewhere else and so it was again sooner and sooner. Dennis Elwell not unl I was well into the store that I Minister of Music The economics of Christmas seems saw them. I saw the Christmas Sharon Parker to intrude earlier every year. The decoraons. Over a full week before Director of Chrisan Educaon Spirit of Christmas endures fewer and Margene Biedermann Halloween! fewer days. Junior Choir Director I stopped short in front of a line of Might I suggest that we re‐channel Jane Rozmiarek white and gliery Christmas trees, our concern, away from the Carol Rozmiarek emblazoned with lights and festooned Interim Office Staff decoraons in our malls and stores, so with products on display. -

ʻtis the Season for Economics!
‘Tis the Season for Economics! ELEMENTARY: A New Coat for Anna by Harriet Ziefert Concepts: barter, goods, services http://blog.richmond.edu/openwidelookinside/archives/315 http://www.econed.org/userfiles/files/New%20Coat%20for%20Anna(1).pdf http://www.econedlink.org/lessons/index.php?lid=699&type=educator http://www.mcee.umn.edu/documents/A%20New%20Coat.pdf http://exchange.smarttech.com/details.html?id=ff28819d-9f1d-46b0-bad4-871b96a9bbf4 http://exchange.smarttech.com/details.html?id=397b4ebd-7ee1-4929-b79c-9e91d35b1de5 A Colonial Christmas in Williamsburg Concepts: consumers, producers, goods, services, wants http://teachers.history.org/resources/lesson-plans/colonial-christmas-williamsburg Econ Songs Concepts: Too many to list. Use familiar and often holiday tunes to teach economics. http://www.kidseconposters.com/activites-and-games/sing-a-longs/ How Santa Got His Job by Stephen Krensky Concepts: Human Resources, human capital http://www.kidseconposters.com/literature-connection/human-resources/how-santa-got-his- job/?back=literature If You Take a Mouse to the Movies by Laura Numeroff Concepts: Unlimited wants, production While both of these links are for If You Give a Mouse a Cookie, they are easily adapted. Students can create stockings full of wants, produce Christmas cookies or ornaments. http://ecedweb.unomaha.edu/lessons/mouse.htm http://blog.richmond.edu/openwidelookinside/archives/1837 http://www.mcee.umn.edu/documents/Give%20a%20Mouse%20a%20Cookie.pdf Messy Bessey’s Holidays by Patricia and Fredrick McKissack Concepts: factors of production, intermediate goods, natural resources, capital resources, human resources Great holiday book! Lesson includes whiteboard interactives http://www.stlouisfed.org/education_resources/messy-besseys-holidays/ Natural Resources and Your Christmas Tree Concept: natural resources http://www.mineralseducationcoalition.org/pdfs/xmastree.pdf Toys for Me: A Lesson on Choice Concepts: choice, opportunity cost, economic wants Too Many Toys by David Shannon is a wonderful connection for this lesson. -

Woodland Owners Guide to Internet Resources: States of the Northeast Biodiversity/Threatened and Endangered Species
1 The Northeastern Area is a USDA Forest Service designation for the 20 States and the District of Columbia as shown on the map above and listed below: Connecticut Maryland New York Delaware Massachusetts Ohio District of Columbia Michigan Pennsylvania Illinois Minnesota Rhode Island Indiana Missouri Vermont Iowa New Hampshire West Virginia Maine New Jersey Wisconsin The U.S. Department of Agriculture (USDA) prohibits discrimination in all its programs and activities on the basis of race, color, national origin, sex, religion, age, disability, political beliefs, sexual orientation, or marital or family status. (Not all prohibited bases apply to all programs.) Persons with disabilities who require alternative means for communication of program information (Braille, large print, audiotape, etc.) should contact USDA's TARGET Center at (202) 720−2600 (voice and TDD). To file a complaint of discrimination, write USDA, Director, Office of Civil Rights, Room 326−W, Whitten Building, 1400 Independence Avenue, SW, Washington, D.C. 20250−9410 or call (202) 720−5964 (voice and TDD). USDA is an equal opportunity provider and employer. 2 This listing of internet resources was developed to provide you, the Non−Industrial Private Forest (NIPF) landowner, with a better understanding of the information and resources available on the internet relating to forest stewardship. In browsing the document, you’ll hopefully find links to areas you’re already interested in, and perhaps also find your interest captured by other, previously unfamiliar, aspects of forest stewardship. The selection of sites presented here is not intended to represent everything of possible interest to the NIPF landowner, nor should inclusion be considered an endorsement. -
![[Enter Title Here]](https://docslib.b-cdn.net/cover/6434/enter-title-here-3906434.webp)
[Enter Title Here]
Frontier Economics Bulletin Water Energy Reindeer Environment Transport Financial services Healthcare Telecoms Father Christmas Competition policy Policy analysis and design Contract design and evaluation Chestnuts roasting on an open fire Retail Strategy Market design DECEMBER 2011 Present values THE ECONOMICS OF CHRISTMAS It’s easier to think of economists as the prophets of trading doom than as Santa’s little helpers – too busy telling everybody what’s happening to productivity, energy demand and like-for-like sales to provide any insights into the annual exchange of goodwill and good- or-ill gifts to family and friends. So Frontier Economics has been scouring the academic literature of behavioural economics for tips to make that last struggle with your present list a little easier… With so much, for retailers, hanging on their Christmas trade, it’s not surprising that economists have been attempting to analyse present-giving for years. Most of the research, however, has a narrow, distinctly Scrooge-like tone to it (maybe too much of it was conducted by analysts soured by their annual quota of socks). So what follows is an attempt to elicit slightly more seasonal cheer – and even a little buyers’ guidance – from the available stock of behavioural economics and consumer psychology. 2 Frontier Economics | December 2011 THOUGHT PROFIT AND DEADWEIGHT LOSS Present buying isn’t easy. Ideally, we would give something whose value to the recipient is greater than its cost, having found something original and beautiful that surprises and delights. But the risk is that the value to the recipient is actually lower than the cost: it’s just not something he or she wanted. -
![Journal De La Société Des Américanistes, 88 | 2002, « Tome 88 » [En Ligne], Mis En Ligne Le 04 Février 2005, Consulté Le 24 Septembre 2020](https://docslib.b-cdn.net/cover/5244/journal-de-la-soci%C3%A9t%C3%A9-des-am%C3%A9ricanistes-88-2002-%C2%AB-tome-88-%C2%BB-en-ligne-mis-en-ligne-le-04-f%C3%A9vrier-2005-consult%C3%A9-le-24-septembre-2020-4865244.webp)
Journal De La Société Des Américanistes, 88 | 2002, « Tome 88 » [En Ligne], Mis En Ligne Le 04 Février 2005, Consulté Le 24 Septembre 2020
Journal de la Société des américanistes 88 | 2002 tome 88 Édition électronique URL : http://journals.openedition.org/jsa/138 DOI : 10.4000/jsa.138 ISSN : 1957-7842 Éditeur Société des américanistes Édition imprimée Date de publication : 1 janvier 2002 ISSN : 0037-9174 Référence électronique Journal de la Société des américanistes, 88 | 2002, « tome 88 » [En ligne], mis en ligne le 04 février 2005, consulté le 24 septembre 2020. URL : http://journals.openedition.org/jsa/138 ; DOI : https://doi.org/ 10.4000/jsa.138 Ce document a été généré automatiquement le 24 septembre 2020. © Société des Américanistes 1 SOMMAIRE Articles La description du Grand Temple de Mexico par Bernardino de Sahagún (Codex de Florence, annexe du Livre II) Aurélie Couvreur Elementos humboldtianos en las teorías de la religión y de la magia de Konrad Th. Preuss Paulina Alcocer Faire le mythe. Histoire, récit et transformation en Amazonie Carlos Fausto Suicide « à la kashinawa ». Le désir de l’au-delà ou la séduction olfactive et auditive par les esprits des morts Barbara Keifenheim El testimonio de Joaquina Grefa, una cautiva quichua entre los huaorani (Ecuador, 1945) María Susana Cipolletti Os enviados de Dom Bosco entre os Masiripiwëiteri. O impacto missionário sobre o sistema social e cultural dos Yanomami ocidentais (Amazonas, Brasil) Maria Inês Smiljanic Quilombolas et évangéliques : une incompatibilité identitaire ? Réflexions à partir d’une étude de cas en Amazonie brésilienne Véronique Boyer Marrons, colons, contrebandiers. Réseaux transversaux et configuration -
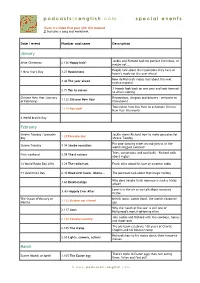
Special Days List
p o d c a s t s i n e n g l i s h .com special events There is a video that goes with this podcast ♬ Includes a song and worksheet Date / event Number and name Description January Jackie and Richard had the perfect Christmas, or After Christmas 2.156 Happy hols? maybe not... People talk about the resolutions they have or 1 New Year's Day 3.27 Resolutions haven't made for the year ahead How do Richard's mates feel about the next 3.44 The year ahead twelve months? 3 friends look back on one year and look forward 2.71 Ten to eleven to what's coming Chinese New Year (January Decorations, dragons and dancers - welcome to 1.122 Chinese New Year or February) Chinatown! Two videos from Ken Hom to celebrate Chinese 1.114 Hot wok! New Year this month 4 World Braille Day February Shrove Tuesday / pancake Jackie shows Richard how to make pancakes for 1.28 Pancake day day Shrove Tuesday Put your dancing shoes on and join us at the Shrove Tuesday 3.94 Samba sensation world's biggest carnival! Tries, conversions and oval balls - Richard talks First weekend 2.59 The 6 nations about rugby! 13 World Radio Day (UN) 3.29 The radio ham Frank talks about his love of amateur radio 14 Valentine's Day 2.43 Head over heels. Idioms... The pie team talk about that magic feeling Why does Sandra think romance is such a tricky 3.60 Relationships affair? Love is in the air as we talk about romantic 3.43 Happily Ever After fiction The Oscars (February or British icons: James Bond, the world's favourite 3.122 Shaken not stirred March) spy Why the "teeth of the sea" is still one of 2.117 Jaws Hollywood's most frightening films Join Jackie and Richard with the cowboys, horses 2.120 Cowboy country and shoot-outs The pie team celebrate 100 years of Charlie 2.105 The tramp Chaplin and his famous tramp Richard chats to his mates about their favourite 2.30 Lights, camera, action! movies March There's more to Easter eggs than just eating Easter (March or April) 1.105 The Easter egg them, listen and find out! © w w w . -
Times-Call Inventory H
Times-Call # Title of File Folder Photo# Brief Description H.30.10 Holidays - Pictures 1967-1971 37 8 undated photographs. Holidays - American Education Week H.30.10 1987-1988 0 November, American Education Week 1987-1988. H.30.10 Holidays - April Fool's Day 1973 13 1 photo/article from 1971, April Fool's section of paper, history of April Fool's day. H.30.10 Holidays - Arbor Day 1972-1990 17 3 undated photos, Arbor Day 1972-1990. H.30.10 Holidays - Ash Wednesday 1979 0 Ash Wednesday 1979. Holidays - Chinese New Year -- Food H.30.10 1985-1991 3 Original call number B.70.10 34 undated photos, 1 photo from 1988. 1 photo from 1990, no clippings -- entire H.30.10 Holidays - Christmas Tabs 1991-1995 52 sections of the newspaper preserved, Christmas advertising inserts. H.30.10 Holidays - Christmas 1991-1993 50 27 undated photos, 1 photo from 1989, entire sections preserved. 6 undated photos, 1 photo from 1989, 1 photo from 1987, entire sections preserved, H.30.10 Holidays - Christmas 1990 36 series on homelessness/unemployment in Longmont. H.30.10 Holidays - Christmas 1989 87 50 undated photos, Christmas 1989. H.30.10 Holidays - Christmas 1988 7 Entire sections preserved, Christmas 1988. H.30.10 Holidays - Christmas 1987 41 3 undated photos, City of Longmont's efforts to buy new Christmas decorations. H.30.10 Holidays - Christmas 1986 32 1 scanned photo, 1 undated photo, entire sections preserved, Christmas 1986. H.30.10 Holidays - Christmas 1985 18 2 undated photos, Christmas 1985. 13 undated photos (inc.