Digital Baseband Communication Systems for More Information: Read Chapters 1, 6 and 7 in Your Textbook Or Visit
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Criteria for Choosing Line Codes in Data Communication
ISTANBUL UNIVERSITY – YEAR : 2003 (843-857) JOURNAL OF ELECTRICAL & ELECTRONICS ENGINEERING VOLUME : 3 NUMBER : 2 CRITERIA FOR CHOOSING LINE CODES IN DATA COMMUNICATION Demir Öner Istanbul University, Engineering Faculty, Electrical and Electronics Engineering Department Avcılar, 34850, İstanbul, Turkey E-mail: [email protected] ABSTRACT In this paper, line codes used in data communication are investigated. The need for the line codes is emphasized, classification of line codes is presented, coding techniques of widely used line codes are explained with their advantages and disadvantages and criteria for chosing a line code are given. Keywords: Line codes, correlative coding, criteria for chosing line codes.. coding is either performed just before the 1. INTRODUCTION modulation or it is combined with the modulation process. The place of line coding in High-voltage-high-power pulse current The transmission systems is shown in Figure 1. purpose of applying line coding to digital signals before transmission is to reduce the undesirable The line coder at the transmitter and the effects of transmission medium such as noise, corresponding decoder at the receiver must attenuation, distortion and interference and to operate at the transmitted symbol rate. For this ensure reliable transmission by putting the signal reason, epecially for high-speed systems, a into a form that is suitable for the properties of reasonably simple design is usually essential. the transmission medium. For example, a sampled and quantized signal is not in a suitable form for transmission. Such a signal can be put 2. ISSUES TO BE CONSIDERED IN into a more suitable form by coding the LINE CODING quantized samples. -

Vpisystems—Demonstration Examples
Appendix VPIsystems—Demonstration Examples Introduction The following 12 examples have been added to demonstrate important engineering aspects of Chapter 3. The user can play with each example in real time by accessing the website http://www.vpiphotonics.com/VPIplayer.php. This particular website is maintained by VPIsystems GmbH and it is provided at no cost to the user. Any difficulties opening the website or any software improperly functioning should be addressed directly to VPIsystems GmbH, Carnotstr. 6, 10587 Berlin, Germany, Phone +49 30 398 058-0, Fax +49 30 398 058-58 Application Example 1 Title System impairments in 10 Gbps NRZ-based WDM transmissions Description This setup illustrates the impact of ASE noise and fiber nonlinearities on the performance of a 10 Gbps NRZ-based WDM system. The BER of each channel can be investigated individually. The user can adjust the number of spans (transmission length), switch off/on the fiber nonlinear- ities and modify the EDFA noise figure. Application Example 2 Title Performance of NRZ, RZ, and Duobinary modulation format in 10 Gbps transmission Description The setup compares the performance of the NRZ, RZ, and Duobinary modulation formats in a single channel 10 Gbps transmission. The BER obtained with each modulation format are displayed against the accumulated dispersion or the OSNR. The user can adjust the OSNR (respectively the accumulated dispersion) as well as the 3 dB bandwidth of the optical filter in front of the receiver. S. V. Kartalopoulos, Next Generation Intelligent Optical Networks, 257 C Springer 2008 258 Appendix: VPIsystems—Demonstration Examples Application Example 3 Title Performance comparison of NRZ, DPSK, and DQPSK in 40 Gbps transmission Description The setup investigates the performance of NRZ, DPSK, and DQPSK modulation in a single channel 40 Gbps transmission. -
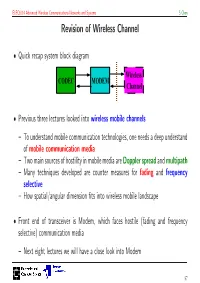
Revision of Wireless Channel
ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Revision of Wireless Channel • Quick recap system block diagram Wireless CODEC MODEM Channel • Previous three lectures looked into wireless mobile channels – To understand mobile communication technologies, one needs a deep understand of mobile communication media – Two main sources of hostility in mobile media are Doppler spread and multipath – Many techniques developed are counter measures for fading and frequency selective – How spatial/angular dimension fits into wireless mobile landscape • Front end of transceiver is Modem, which faces hostile (fading and frequency selective) communication media – Next eight lectures we will have a close look into Modem 57 ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Digital Modulation Overview In Digital Coding and Transmission, we learn schematic of MODEM (modulation and demodulation) • with its basic components: clock carrier pulse b(k) x(k) x(t) s(t) pulse Tx filter bits to modulat. symbols generator GT (f) clock carrier channel recovery recovery GC (f) ^ b(k) x(k)^x(t) ^s(t) ^ symbols sampler/ Rx filter AWGN demodul. + to bits decision GR (f) n(t) The purpose of MODEM: transfer the bit stream at required rate over the communication medium • reliably – Given system bandwidth and power resource 58 ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Constellation Diagram • Digital modulation signal has finite states. This manifests in symbol (message) set: M = {m1, m2, ··· , mM }, where each symbol contains log2 M bits • Or in modulation signal set: S = {s1(t),s2(t), ··· sM (t)}. There is one-to-one relationship between two sets: modulation scheme M S ←→ Q • Example: BPSK, M = 2. -

CLASS 341 CODED DATA GENERATION OR CONVERSION January 2011
CLASS 341 CODED DATA GENERATION OR CONVERSION 341 - 1 341 CODED DATA GENERATION OR CONVERSION 1 DIGITAL PATTERN READING TYPE 50 DIGITAL CODE TO DIGITAL CODE CONVERTER CONVERTERS 2 .Plural denominationally related 51 .Adaptive coding carriers (e.g., coarse/fine 52 .To or from particular bit symbol geared discs) 53 ..Bit represented by pulse width 3 .Plural types of codes on single 54 ..Bit represented by discrete carrier frequency 4 .According to nonlinear function 55 .Substituting specified bit 5 .For X or Y coordinate combinations for other determination (e.g., stylus- prescribed bit combinations pad) 56 .To or from multi-level codes 6 .With directional discrimination 57 ..Binary to or from ternary 7 .Antiambiguity feature 58 .To or from minimum d.c. level 8 .Real and complementary patterns codes 9 .Having combined (e.g., 59 .To or from run length limited denominational, combination codes code) coding pattern 60 .To or from packed format 10 ..Constant distance code 61 .Data rate conversion 11 .Incremental 62 .BCD (binary-coded-decimal) to or 12 .Cathode ray from decimal 13 .Optical 63 .To or from bit count codes 14 ..Having optical waveguide 64 .To or from number of pulses 15 .Magnetic, inductive or 65 ..To or from Huffman codes capacitive 66 ..To or from Morse code 16 .Brush and contacts or conductive 67 .To or from variable length codes pattern 68 .To or from NRZ (nonreturn-to- 17 .Actuated by physical projection zero) codes 20 BODILY ACTUATED CODE GENERATOR 69 ..Return-to-zero to or from NRZ 21 .For handicapped user (nonreturn-to-zero) -

Pulse Shape Filtering in Wireless Communication-A Critical Analysis
(IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 2, No.3, March 2011 Pulse Shape Filtering in Wireless Communication-A Critical Analysis A. S Kang Vishal Sharma Assistant Professor, Deptt of Electronics and Assistant Professor, Deptt of Electronics and Communication Engg Communication Engg SSG Panjab University Regional Centre University Institute of Engineering and Technology Hoshiarpur, Punjab, INDIA Panjab University Chandigarh - 160014, INDIA [email protected] [email protected] Abstract—The goal for the Third Generation (3G) of mobile networks. The standard that has emerged is based on ETSI's communications system is to seamlessly integrate a wide variety Universal Mobile Telecommunication System (UMTS) and is of communication services. The rapidly increasing popularity of commonly known as UMTS Terrestrial Radio Access (UTRA) mobile radio services has created a series of technological [1]. The access scheme for UTRA is Direct Sequence Code challenges. One of this is the need for power and spectrally Division Multiple Access (DSCDMA). The information is efficient modulation schemes to meet the spectral requirements of spread over a band of approximately 5 MHz. This wide mobile communications. Pulse shaping plays a crucial role in bandwidth has given rise to the name Wideband CDMA or spectral shaping in the modern wireless communication to reduce WCDMA.[8-9] the spectral bandwidth. Pulse shaping is a spectral processing technique by which fractional out of band power is reduced for The future mobile systems should support multimedia low cost, reliable , power and spectrally efficient mobile radio services. WCDMA systems have higher capacity, better communication systems. It is clear that the pulse shaping filter properties for combating multipath fading, and greater not only reduces inter-symbol interference (ISI), but it also flexibility in providing multimedia services with defferent reduces adjacent channel interference. -

Fiber Optic Communications
FIBER OPTIC COMMUNICATIONS EE4367 Telecom. Switching & Transmission Prof. Murat Torlak Optical Fibers Fiber optics (optical fibers) are long, thin strands of very pure glass about the size of a human hair. They are arranged in bundles called optical cables and used to transmit signals over long distances. EE4367 Telecom. Switching & Transmission Prof. Murat Torlak Fiber Optic Data Transmission Systems Fiber optic data transmission systems send information over fiber by turning electronic signals into light. Light refers to more than the portion of the electromagnetic spectrum that is near to what is visible to the human eye. The electromagnetic spectrum is composed of visible and near -infrared light like that transmitted by fiber, and all other wavelengths used to transmit signals such as AM and FM radio and television. The electromagnetic spectrum. Only a very small part of it is perceived by the human eye as light. EE4367 Telecom. Switching & Transmission Prof. Murat Torlak Fiber Optics Transmission Low Attenuation Very High Bandwidth (THz) Small Size and Low Weight No Electromagnetic Interference Low Security Risk Elements of Optical Transmission Electrical-to-optical Transducers Optical Media Optical-to-electrical Transducers Digital Signal Processing, repeaters and clock recovery. EE4367 Telecom. Switching & Transmission Prof. Murat Torlak Types of Optical Fiber Multi Mode : (a) Step-index – Core and Cladding material has uniform but different refractive index. (b) Graded Index – Core material has variable index as a function of the radial distance from the center. Single Mode – The core diameter is almost equal to the wave length of the emitted light so that it propagates along a single path. -

Adv. Communication Lab 6Th Sem E&C
TH ADV. COMMUNICATION LAB 6 SEM E&C • the line-coded signal can directly be put on a transmission line, in the form of variations of the voltage or current (often using differential signaling). • the line-coded signal (the "base-band signal") undergoes further pulse shaping (to reduce its frequency bandwidth) LINE CODING and then modulated (to shift its frequency bandwidth) to create the "RF signal" that can be sent through free space. Line coding consists of representing the digital signal to be • the line-coded signal can be used to turn on and off a light transported by an amplitude- and time-discrete signal that is in Free Space Optics, most commonly infrared remote optimally tuned for the specific properties of the physical channel control. (and of the receiving equipment). The waveform pattern of • the line-coded signal can be printed on paper to create a voltage or current used to represent the 1s and 0s of a digital bar code. data on a transmission link is called line encoding. The common • the line-coded signal can be converted to a magnetized types of line encoding are unipolar, polar, bipolar and spots on a hard drive or tape drive. Manchester encoding. • the line-coded signal can be converted to a pits on optical For reliable clock recovery at the receiver, one usually imposes a disc. maximum run length constraint on the generated channel Unfortunately, most long-distance communication sequence, i.e. the maximum number of consecutive ones or channels cannot transport a DC component. The DC zeros is bounded to a reasonable number. -

Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation
Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation A Communication System Dig. Baseband Modulators (Line Coders) • Sequence of bits are modulated into waveforms before transmission • à Digital transmission system consists of: • The modulator is based on: • The symbol mapper takes bits and converts them into symbols an) – this is done based on a given table • Pulse Shaping Filter generates the Gaussian pulse or waveform ready to be transmitted (Baseband signal) Waveform; Sampled at T Pulse Amplitude Modulation (PAM) Example: Binary PAM Example: Quaternary PAN PAM Randomness • Since the amplitude level is uniquely determined by k bits of random data it represents, the pulse amplitude during the nth symbol interval (an) is a discrete random variable • s(t) is a random process because pulse amplitudes {an} are discrete random variables assuming values from the set AM • The bit period Tb is the time required to send a single data bit • Rb = 1/ Tb is the equivalent bit rate of the system PAM T= Symbol period D= Symbol or pulse rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate • If quaternary signaling & pulse rate is 9600 find bit rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 • If quaternary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 Binary Line Coding Techniques • Line coding - Mapping of binary information sequence into the digital signal that enters the baseband channel • Symbol mapping – Unipolar - Binary 1 is represented by +A volts pulse and binary 0 by no pulse during a bit period – Polar - Binary 1 is represented by +A volts pulse and binary 0 by –A volts pulse. -

ECE 463 Lab 3: Pulse Shaping and Matched Filtering
UIUC ECE 463 Digital Communication Laboratory Fall 2018 ECE 463 Lab 3: Pulse Shaping and Matched Filtering 1. Introduction The objective of this lab session is to introduce the basic concepts of pulse shaping, matched filter and pulse alignment. In digital communication, the message in digital must be converted into an analog signal to be transmitted. This conversion is done by the pulse shaping filter, which changes each symbol into a suitable analog pulse. Designing the pulse shape is important because the spectrum of the pulse dictates the spectrum of the whole transmission. However, to confine the spectrum, we have to smooth the pulse with slow transition. This requires the pulse extending beyond a symbol time, which introduces inter- symbol interference (ISI). Thus, there is a trade-off between the bandwidth and the ISI of the pulse shape. After transmission, the matched filter helps to recapture the symbols from the received pulses. The matched filter is aimed at reducing the sensitivity of noise by maximizing the signal-to-noise ratio (SNR) and minimizing the ISI at the receiver. In a more realistic channel model, the receiver never knows the precise arrival time of the pulse. Therefore, the receiver must know the exact symbol timing in order to correctly demodulate the transmitted symbols from the transmitter. 1.1. Contents 1. Introduction 2. Pulse Shaping 3. Matched Filtering 4. Pulse Alignment (Symbol Timing Recovery) 1.2. Report Submit the answers, figures and the discussions on all the questions. The report is due as a hard copy at the beginning of the next lab. -

Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems
Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems Erkin Cubukcu Abstract This presentation briefly discusses application of the Root Raised Cosine (RRC) pulse shaping in the space telecommunication. Use of the RRC filtering (i.e., pulse shaping) is adopted in commercial communications, such as cellular technology, and used extensively. However, its use in space communication is still relatively new. This will possibly change as the crowding of the frequency spectrum used in the space communication becomes a problem. The two conflicting requirements in telecommunication are the demand for high data rates per channel (or user) and need for more channels, i.e., more users. Theoretically as the channel bandwidth is increased to provide higher data rates the number of channels allocated in a fixed spectrum must be reduced. Tackling these two conflicting requirements at the same time led to the development of the RRC filters. More channels with wider bandwidth might be tightly packed in the frequency spectrum achieving the desired goals. A link model with the RRC filters has been developed and simulated. Using 90% power Bandwidth (BW) measurement definition showed that the RRC filtering might improve spectrum efficiency by more than 75%. Furthermore using the matching RRC filters both in the transmitter and receiver provides the improved Bit Error Rate (BER) performance. In this presentation the theory of three related concepts, namely pulse shaping, Inter Symbol Interference (ISI), and Bandwidth (BW) will be touched -

Digital Phase Modulation: a Review of Basic Concepts
Digital Phase Modulation: A Review of Basic Concepts James E. Gilley Chief Scientist Transcrypt International, Inc. [email protected] August , Introduction The fundamental concept of digital communication is to move digital information from one point to another over an analog channel. More specifically, passband dig- ital communication involves modulating the amplitude, phase or frequency of an analog carrier signal with a baseband information-bearing signal. By definition, fre- quency is the time derivative of phase; therefore, we may generalize phase modula- tion to include frequency modulation. Ordinarily, the carrier frequency is much greater than the symbol rate of the modulation, though this is not always so. In many digital communications systems, the analog carrier is at a radio frequency (RF), hundreds or thousands of MHz, with information symbol rates of many megabaud. In other systems, the carrier may be at an audio frequency, with symbol rates of a few hundred to a few thousand baud. Although this paper primarily relies on examples from the latter case, the concepts are applicable to the former case as well. Given a sinusoidal carrier with frequency: fc , we may express a digitally-modulated passband signal, S(t), as: S(t) A(t)cos(2πf t θ(t)), () = c + where A(t) is a time-varying amplitude modulation and θ(t) is a time-varying phase modulation. For digital phase modulation, we only modulate the phase of the car- rier, θ(t), leaving the amplitude, A(t), constant. BPSK We will begin our discussion of digital phase modulation with a review of the fun- damentals of binary phase shift keying (BPSK), the simplest form of digital phase modulation. -

Codificação De Dados Códigos De Transmissão E Modulações Digitais
C 1 Codificação de Dados Códigos de Transmissão e Modulações Digitais FEUP/DEEC RCOM – 2006/07 MPR/JAR C 2 Representação de Dados » Dados digitais, sinal digital » Dados analógicos, sinal digital » Dados digitais, sinal analógico » Dados analógicos, sinal analógico C 3 Dados Digitais, Sinal Digital (Códigos de Transmissão) ♦ Admitimos, sem perda de generalidade, que a informação digital é representada por um código binário, isto é, os dados a transmitir constituem uma sequência de símbolos de um alfabeto binário (0 e 1) ♦ Para transmissão num canal passa-baixo, os dados binários podem ser representados directamente por um sinal digital, isto é, por uma sequência de impulsos que se sucedem a uma cadência fixa (sincronizada por um relógio) » No caso mais simples cada símbolo binário é representado por um sinal elementar que pode ter um de dois níveis (transmissão binária) » É possível agrupar símbolos binários e representar grupos de símbolos binários (dibit, tribit, etc.) por impulsos que podem ter um de L níveis (L = 4, 8, …). A frequência dos sinais elementares (modulation rate), expressa em baud, deixa de ser igual à frequência dos símbolos binários iniciais (data rate), expressa em bit/s, excepto no caso em que L = 2 DR = MR log2 L DR = 1 / T2 L = 4 DR = 2 MR TL = T2 log2 L MR = 1 / TL T4 = 2 T2 » É possível estabelecer outro tipo de relações entre os dados binários e a sequência de sinais elementares que os representam. Os Códigos de Transmissão exploram estas relações; um “símbolo” do código pode ser constituído pela combinação de