Spline Pulse Shaping with Isi-Free Matched Filter Receiver
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
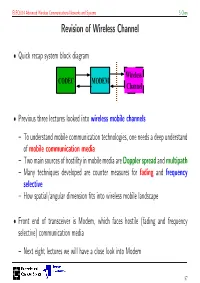
Revision of Wireless Channel
ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Revision of Wireless Channel • Quick recap system block diagram Wireless CODEC MODEM Channel • Previous three lectures looked into wireless mobile channels – To understand mobile communication technologies, one needs a deep understand of mobile communication media – Two main sources of hostility in mobile media are Doppler spread and multipath – Many techniques developed are counter measures for fading and frequency selective – How spatial/angular dimension fits into wireless mobile landscape • Front end of transceiver is Modem, which faces hostile (fading and frequency selective) communication media – Next eight lectures we will have a close look into Modem 57 ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Digital Modulation Overview In Digital Coding and Transmission, we learn schematic of MODEM (modulation and demodulation) • with its basic components: clock carrier pulse b(k) x(k) x(t) s(t) pulse Tx filter bits to modulat. symbols generator GT (f) clock carrier channel recovery recovery GC (f) ^ b(k) x(k)^x(t) ^s(t) ^ symbols sampler/ Rx filter AWGN demodul. + to bits decision GR (f) n(t) The purpose of MODEM: transfer the bit stream at required rate over the communication medium • reliably – Given system bandwidth and power resource 58 ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Constellation Diagram • Digital modulation signal has finite states. This manifests in symbol (message) set: M = {m1, m2, ··· , mM }, where each symbol contains log2 M bits • Or in modulation signal set: S = {s1(t),s2(t), ··· sM (t)}. There is one-to-one relationship between two sets: modulation scheme M S ←→ Q • Example: BPSK, M = 2. -

Pulse Shape Filtering in Wireless Communication-A Critical Analysis
(IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 2, No.3, March 2011 Pulse Shape Filtering in Wireless Communication-A Critical Analysis A. S Kang Vishal Sharma Assistant Professor, Deptt of Electronics and Assistant Professor, Deptt of Electronics and Communication Engg Communication Engg SSG Panjab University Regional Centre University Institute of Engineering and Technology Hoshiarpur, Punjab, INDIA Panjab University Chandigarh - 160014, INDIA [email protected] [email protected] Abstract—The goal for the Third Generation (3G) of mobile networks. The standard that has emerged is based on ETSI's communications system is to seamlessly integrate a wide variety Universal Mobile Telecommunication System (UMTS) and is of communication services. The rapidly increasing popularity of commonly known as UMTS Terrestrial Radio Access (UTRA) mobile radio services has created a series of technological [1]. The access scheme for UTRA is Direct Sequence Code challenges. One of this is the need for power and spectrally Division Multiple Access (DSCDMA). The information is efficient modulation schemes to meet the spectral requirements of spread over a band of approximately 5 MHz. This wide mobile communications. Pulse shaping plays a crucial role in bandwidth has given rise to the name Wideband CDMA or spectral shaping in the modern wireless communication to reduce WCDMA.[8-9] the spectral bandwidth. Pulse shaping is a spectral processing technique by which fractional out of band power is reduced for The future mobile systems should support multimedia low cost, reliable , power and spectrally efficient mobile radio services. WCDMA systems have higher capacity, better communication systems. It is clear that the pulse shaping filter properties for combating multipath fading, and greater not only reduces inter-symbol interference (ISI), but it also flexibility in providing multimedia services with defferent reduces adjacent channel interference. -

Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation
Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation A Communication System Dig. Baseband Modulators (Line Coders) • Sequence of bits are modulated into waveforms before transmission • à Digital transmission system consists of: • The modulator is based on: • The symbol mapper takes bits and converts them into symbols an) – this is done based on a given table • Pulse Shaping Filter generates the Gaussian pulse or waveform ready to be transmitted (Baseband signal) Waveform; Sampled at T Pulse Amplitude Modulation (PAM) Example: Binary PAM Example: Quaternary PAN PAM Randomness • Since the amplitude level is uniquely determined by k bits of random data it represents, the pulse amplitude during the nth symbol interval (an) is a discrete random variable • s(t) is a random process because pulse amplitudes {an} are discrete random variables assuming values from the set AM • The bit period Tb is the time required to send a single data bit • Rb = 1/ Tb is the equivalent bit rate of the system PAM T= Symbol period D= Symbol or pulse rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate • If quaternary signaling & pulse rate is 9600 find bit rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 • If quaternary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 Binary Line Coding Techniques • Line coding - Mapping of binary information sequence into the digital signal that enters the baseband channel • Symbol mapping – Unipolar - Binary 1 is represented by +A volts pulse and binary 0 by no pulse during a bit period – Polar - Binary 1 is represented by +A volts pulse and binary 0 by –A volts pulse. -

ECE 463 Lab 3: Pulse Shaping and Matched Filtering
UIUC ECE 463 Digital Communication Laboratory Fall 2018 ECE 463 Lab 3: Pulse Shaping and Matched Filtering 1. Introduction The objective of this lab session is to introduce the basic concepts of pulse shaping, matched filter and pulse alignment. In digital communication, the message in digital must be converted into an analog signal to be transmitted. This conversion is done by the pulse shaping filter, which changes each symbol into a suitable analog pulse. Designing the pulse shape is important because the spectrum of the pulse dictates the spectrum of the whole transmission. However, to confine the spectrum, we have to smooth the pulse with slow transition. This requires the pulse extending beyond a symbol time, which introduces inter- symbol interference (ISI). Thus, there is a trade-off between the bandwidth and the ISI of the pulse shape. After transmission, the matched filter helps to recapture the symbols from the received pulses. The matched filter is aimed at reducing the sensitivity of noise by maximizing the signal-to-noise ratio (SNR) and minimizing the ISI at the receiver. In a more realistic channel model, the receiver never knows the precise arrival time of the pulse. Therefore, the receiver must know the exact symbol timing in order to correctly demodulate the transmitted symbols from the transmitter. 1.1. Contents 1. Introduction 2. Pulse Shaping 3. Matched Filtering 4. Pulse Alignment (Symbol Timing Recovery) 1.2. Report Submit the answers, figures and the discussions on all the questions. The report is due as a hard copy at the beginning of the next lab. -

Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems
Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems Erkin Cubukcu Abstract This presentation briefly discusses application of the Root Raised Cosine (RRC) pulse shaping in the space telecommunication. Use of the RRC filtering (i.e., pulse shaping) is adopted in commercial communications, such as cellular technology, and used extensively. However, its use in space communication is still relatively new. This will possibly change as the crowding of the frequency spectrum used in the space communication becomes a problem. The two conflicting requirements in telecommunication are the demand for high data rates per channel (or user) and need for more channels, i.e., more users. Theoretically as the channel bandwidth is increased to provide higher data rates the number of channels allocated in a fixed spectrum must be reduced. Tackling these two conflicting requirements at the same time led to the development of the RRC filters. More channels with wider bandwidth might be tightly packed in the frequency spectrum achieving the desired goals. A link model with the RRC filters has been developed and simulated. Using 90% power Bandwidth (BW) measurement definition showed that the RRC filtering might improve spectrum efficiency by more than 75%. Furthermore using the matching RRC filters both in the transmitter and receiver provides the improved Bit Error Rate (BER) performance. In this presentation the theory of three related concepts, namely pulse shaping, Inter Symbol Interference (ISI), and Bandwidth (BW) will be touched -

Digital Phase Modulation: a Review of Basic Concepts
Digital Phase Modulation: A Review of Basic Concepts James E. Gilley Chief Scientist Transcrypt International, Inc. [email protected] August , Introduction The fundamental concept of digital communication is to move digital information from one point to another over an analog channel. More specifically, passband dig- ital communication involves modulating the amplitude, phase or frequency of an analog carrier signal with a baseband information-bearing signal. By definition, fre- quency is the time derivative of phase; therefore, we may generalize phase modula- tion to include frequency modulation. Ordinarily, the carrier frequency is much greater than the symbol rate of the modulation, though this is not always so. In many digital communications systems, the analog carrier is at a radio frequency (RF), hundreds or thousands of MHz, with information symbol rates of many megabaud. In other systems, the carrier may be at an audio frequency, with symbol rates of a few hundred to a few thousand baud. Although this paper primarily relies on examples from the latter case, the concepts are applicable to the former case as well. Given a sinusoidal carrier with frequency: fc , we may express a digitally-modulated passband signal, S(t), as: S(t) A(t)cos(2πf t θ(t)), () = c + where A(t) is a time-varying amplitude modulation and θ(t) is a time-varying phase modulation. For digital phase modulation, we only modulate the phase of the car- rier, θ(t), leaving the amplitude, A(t), constant. BPSK We will begin our discussion of digital phase modulation with a review of the fun- damentals of binary phase shift keying (BPSK), the simplest form of digital phase modulation. -

PAM Communication System Impulse Modulator
PAM Communication System {Ex: -3,-1,1,3} Binary Impulse Pulse message Mapping Modulation sequence Modulator Shaping π Cos(2 fct) Digital data transmission using pulse amplitude modulation (PAM) Bit rate Rd bits/sec Input bits are blocked into J-bit words and mapped into the sequence of symbols mk which are selected from an alphabet of M=2J distinct voltage levels fs=Rd/J is the symbol rate (baud rate) Impulse modulator Represent the symbol sequence by the Dirac impulse train The impulse modulator block forms this function. This impulse train is applied to a transmit pulse shaping filter so that the signal is band limited to the channel bandwidth. 1 Pulse Shaping and PAM When the message signal is digital, it must be converted into an analog signal in order to be transmitted. “pulse shaping” filter changes the symbol into a suitable analog pulse Each symbol w(kT) initiates an analog pulse that is scaled by the value of the signal Pulse Shaping Compose the analog pulse train entering the pulse shaping filter as which is w(kT) for t = kT and 0 for t = kT Pulse shaping filter output 2 Pulse Shaping 4-PAM symbol sequence triggering baud-spaced rectangular pulse Intersymbol Interference If the analog pulse is wider than the time between adjacent symbols, the outputs from adjacent symbols may overlap A problem called intersymbol interference (ISI) What kind of pulses minimize the ISI? Choose a shape that is one at time kT and zero at mT for all m≠k Then, the analog waveform contains only the value from the desired input symbol and no interference from other nearby input symbols. -

ENSC327 Communications Systems 25: ISI and Pulse Shaping (Ch 6)
ENSC327 Communications Systems 25: ISI and Pulse Shaping (Ch 6) Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chapter 6: Baseband Data Transmission No modulation, sending pulse sequences directly Suitable for lowpass channels (eg, coaxial cables) (Chap 7 will study digital bandpass modulation, f or bandpass channels (eg, wireless) that need high-freq carrier) ISI and Pulse Shaping ISI Definition Zero ISI Condition Nyquist Pulse Shaping Condition Nyquist bandwidth Nyquist channel 2 Introduction A digital communication system involves the following operations: Transmitter: maps the digital information to analog electromagnetic energy. Receiver: records the analog electromagnetic energy, and recover the digital information. The system can introduces two kinds of distortions: Channel noise: due to random and unpredictable physical phenomena. Studied in Chap. 9 and 10. Intersymbol interference (ISI) : due to imperfections in the frequency response of the channel. The main issues is that previously transmitted symbols affect the current received symbol. 3 Studied in Chap. 6. 6.1 Baseband Transmission with PAM Input : binary data, bk = 0 or 1, with duration Tb. Bit rate: 1/T b bits/second. Line encoder (Chap. 5): electrical representation of the binary sequences, e.g., + ,1 bk = ,1 ak = b − ,1 k = .0 4 6.1 Baseband Transmission with PAM Transmit filter : use pulses of different amplitudes to represent one or more binary bits. The basic shape is represented by a filter g(t) or G(f) The output discrete PAM signal from the transmitter: 5 6.1 Baseband Transmission with PAM Channel : If the channel is ideal, no distortion will be introduced. -
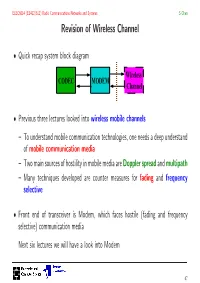
Revision of Wireless Channel
ELEC6014 (EZ412/612) Radio Communications Networks and Systems S Chen Revision of Wireless Channel • Quick recap system block diagram Wireless CODEC MODEM Channel • Previous three lectures looked into wireless mobile channels – To understand mobile communication technologies, one needs a deep understand of mobile communication media – Two main sources of hostility in mobile media are Doppler spread and multipath – Many techniques developed are counter measures for fading and frequency selective • Front end of transceiver is Modem, which faces hostile (fading and frequency selective) communication media Next six lectures we will have a look into Modem 47 ELEC6014 (EZ412/612) Radio Communications Networks and Systems S Chen Digital Modulation Overview • Schematic of MODEM (modulation and demodulation) with its basic components: clock carrier pulse b(k) x(k) x(t) s(t) pulse Tx filter bits to modulat. symbols generator GT (f) clock carrier channel recovery recovery GC (f) ^ b(k) x(k)^x(t) ^s(t) ^ symbols sampler/ Rx filter AWGN demodul. + to bits decision GR (f) n(t) • The purpose of MODEM: transfer the bit stream at certain rate over the communication medium reliably 48 ELEC6014 (EZ412/612) Radio Communications Networks and Systems S Chen Constellation Diagram • Digital modulation signal has finite states. This manifests in symbol (message) set: M = {m1, m2, ··· , mM }, where each symbol contains log2 M bits • Or in modulation signal set: S = {s1(t),s2(t), ··· sM (t)}. There is one-to-one relationship between two sets: modulation scheme M -

Digital Baseband Communication Systems for More Information: Read Chapters 1, 6 and 7 in Your Textbook Or Visit
EE 421: Communications I Prof. Mohammed Hawa Introduction to Digital Baseband Communication Systems For more information: read Chapters 1, 6 and 7 in your textbook or visit http://wikipedia.org/. Remember that communication systems in general can be classified into four categories: Analog Baseband Systems, Analog Carrier Systems ( using analog modulation), Digital Baseband Systems and Digital Carrier Systems ( using digital modulation). Digital baseband and digital carrier transmission systems have many advantages over their analog counterparts. Some of these advantages are: 1. Digital transmission systems are more immune to noise due to threshold detection at the receiver; and the availability of regenerative repeaters, which can be used instead of analog amplifiers at intermediate points throughout the transmission channel. 2. Digital transmission systems allow multiplexing at both the baseband level (e.g., TDM) and carrier level (e.g., FDM, CDMA and OFDMA), which means we can easily carry multiple conversations (signals) on a single physical medium (channel). 3. The ability to use spread spectrum techniques in digital systems help overcome jamming and interference and allows us to hide the transmitted signal within noise if necessary. In addition, the use of orthogonality is easier and allows increasing the transmission rate by overcoming impairments such as fading. 4. The possibility of using channel coding techniques (i.e., error correcting codes) in digital communications reduces bit errors at the receiver (i.e., it effectively improves the signal-to-noise ratio (SNR)). 5. The possibility of using source coding techniques (i.e., compression) in digital communications reduces the amount of bits being transmitted, and hence, allows for more bandwidth efficiency. -

Pulse Shaping and Matched Filtering
LAB 4: PULSE SHAPING AND MATCHED FILTERING I. OVERVIEW The objective of this laboratory session is to introduce the basics of pulse shaping and matched filtering designs in digital communication systems. At the transmitter, we focus on pulse shaping; while at the receiver, we focus on matched filtering. Pulse shaping is the process of shaping pulses to be transmitted based on the symbols generated via modulation (Lab 3). The goal is to make the signal suitable to be transmitted through the communication channel mainly by limiting its effective bandwidth. In the first part of this lab, we build a pulse shaping virtual instrument (VI) that is capable of shaping pulses by lowpass filtering. In the second part, we build a matched filter to the pulse shape to maximize the signal to noise ratio before symbol detection. A general block diagram of a transmitter is given in Fig. 1 below: Fig. 1 – Transmitter block diagram A general block diagram of a receiver is given in Fig. 2 below: 1 Fig. 2 – Receiver block diagram In this lab session we implement the Pulse shaping part at the transmitter and the Matched filter part at the receiver. PART 1: PULSE SHAPING In communications, digital signals need to be mapped to an analog waveform in order to be transmitted over the channel. The mapping process is accomplished in two steps: (i) Mapping from source bits to complex symbols (also known as constellation points), which we learned about in Lab 3 – Part 1: Modulation. (ii) Mapping from complex symbols to analog pulse trains, which is studied in this part. -

Modulation Format Conversion in Future Optical Networks
Modulation Format Conversion in Future Optical Networks Javier Cano Adalid Master Thesis Supervisors: Christophe Peucheret and Jorge Seoane Research Center COM Technical University of Denmark March, 2009 ii Abstract The signal generation and receiver schemes of different modulation formats such as on off keying (OOK) in either non‐return to zero (NRZ) or return to zero (RZ), correlative coding and phase‐shift keying (PSK) are described and numerically simulated. Their receiver sensitivities for back to back structure are numerically simulated at 40 Gb/s and compared. The results show how using balanced reception, DPSK has the benefit of approximately 3 dB. We demonstrate that duobinary modulation is characterized by a higher tolerance to the chromatic dispersion in comparison with NRZ. Conversion techniques between modulation formats are described. Different all optical format conversion based on the mentioned method are discussed. Finally, format conversion from RZ‐OOK to RZ‐DPSK based on HNLF nonlinearities is investigated in great detail and numerically simulated at 40 Gb/s. Some converter requirements such as powers, wavelengths, bandwidths, pulse widths and pulse shapes among other are studied. The results show that shorter pulse widths in control signal for the case of walk‐off presence provide worse conversion. Sensitivity of converted RZ‐DPSK is compared with a conventional 33RZ‐DPSK signal showing a penalty close to 4 dB. Finally, the effect of the control wavelength variation at the input of the converter is investigated when the probe signal corresponds with conventional 33%RZ, 50%RZ and 67%RZ duty cycle. iii Acknowledgements I would like to thank many people who have supported my Telecommunication degree studies and helped me to the process of writing this thesis.