Microscopic Description of Nuclear Fission at Finite Temperature
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HISTORY of LEAD POISONING in the WORLD Dr. Herbert L. Needleman Introduction the Center for Disease Control Classified the Cause
HISTORY OF LEAD POISONING IN THE WORLD Dr. Herbert L. Needleman Introduction The Center for Disease Control classified the causes of disease and death as follows: 50 % due to unhealthy life styles 25 % due to environment 25% due to innate biology and 25% due to inadequate health care. Lead poisoning is an environmental disease, but it is also a disease of life style. Lead is one of the best-studied toxic substances, and as a result we know more about the adverse health effects of lead than virtually any other chemical. The health problems caused by lead have been well documented over a wide range of exposures on every continent. The advancements in technology have made it possible to research lead exposure down to very low levels approaching the limits of detection. We clearly know how it gets into the body and the harm it causes once it is ingested, and most importantly, how to prevent it! Using advanced technology, we can trace the evolution of lead into our environment and discover the health damage resulting from its exposure. Early History Lead is a normal constituent of the earth’s crust, with trace amounts found naturally in soil, plants, and water. If left undisturbed, lead is practically immobile. However, once mined and transformed into man-made products, which are dispersed throughout the environment, lead becomes highly toxic. Solely as a result of man’s actions, lead has become the most widely scattered toxic metal in the world. Unfortunately for people, lead has a long environmental persistence and never looses its toxic potential, if ingested. -

ESTIMATION of FISSION-PRODUCT GAS PRESSURE in URANIUM DIOXIDE CERAMIC FUEL ELEMENTS by Wuzter A
NASA TECHNICAL NOTE NASA TN D-4823 - - .- j (2. -1 "-0 -5 M 0-- N t+=$j oo w- P LOAN COPY: RET rm 3 d z c 4 c/) 4 z ESTIMATION OF FISSION-PRODUCT GAS PRESSURE IN URANIUM DIOXIDE CERAMIC FUEL ELEMENTS by WuZter A. PuuZson una Roy H. Springborn Lewis Reseurcb Center Clevelund, Ohio NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON, D. C. NOVEMBER 1968 i 1 TECH LIBRARY KAFB, NM I 111111 lllll IllH llll lilll1111111111111 Ill1 01317Lb NASA TN D-4823 ESTIMATION OF FISSION-PRODUCT GAS PRESSURE IN URANIUM DIOXIDE CERAMIC FUEL ELEMENTS By Walter A. Paulson and Roy H. Springborn Lewis Research Center Cleveland, Ohio NATIONAL AERONAUTICS AND SPACE ADMINISTRATION For sale by the Clearinghouse for Federal Scientific and Technical Information Springfield, Virginia 22151 - CFSTl price $3.00 ABSTRACl Fission-product gas pressure in macroscopic voids was calculated over the tempera- ture range of 1000 to 2500 K for clad uranium dioxide fuel elements operating in a fast neutron spectrum. The calculated fission-product yields for uranium-233 and uranium- 235 used in the pressure calculations were based on experimental data compiled from various sources. The contributions of cesium, rubidium, and other condensible fission products are included with those of the gases xenon and krypton. At low temperatures, xenon and krypton are the major contributors to the total pressure. At high tempera- tures, however, cesium and rubidium can make a considerable contribution to the total pressure. ii ESTIMATION OF FISSION-PRODUCT GAS PRESSURE IN URANIUM DIOXIDE CERAMIC FUEL ELEMENTS by Walter A. Paulson and Roy H. -

Mercury Education
MERCURY The Slippery, Silent Toxin to Dispose of Carefully You may be surprised to find mercury in your home, business and places you go often. When spilled or not disposed of carefully, it poses a risk to human and ecosystem health. DID YOU KNOW? Mercury is the only metal that is liquid at room Why is Mercury Such a Problem? temperature. Mercury, or quicksilver, is an element that serves many useful 80 purposes – when contained. It conducts electricity, is used in thermometers, thermostats, barometers, blood pressure cuffs and many other everyday items such as some alarm clocks Mercury 200.59 and irons. The most common use is in today’s fluorescent light bulbs that use mercury vapor. Read the reverse The trouble comes when mercury is not disposed of properly for safe ways to or worse, when it spills. Mercury is a toxic element that can dispose of mercury. enter the body through an open wound or by inhaling or ingesting it. It can cause damage to nerves, the liver and kidneys, as well as a number of other symptoms. If mercury is poured down the drain or dumped into the sewer, it seeps into lakes and waterways, a chemical process occurs, converting it to deadly methylmercury, potentially contaminating the fish and animals we eat. When products containing mercury are placed in the trash or poured down the drain, the mercury does not disappear. It ends up in the environment via landfills and wastewater treatment facilities. Now that you know some of the items that contain mercury, you can make Never touch or vacuum up buying decisions that reduce the amount of mercury in your home or office, spilled mercury in any form, and that assure safe disposal of products that contain mercury. -

Mercury Spill Fact Sheet
This fact sheet is intended to be a quick reference tool for people who are involved in a mercury spill and cleanup event. MERCURY Mercury mercury MERCURY MERCURY MERCURY Elemental mercury, also called “quicksilver,” is a heavy, silvery, form of the metal mercury that is liquid at room temperature. It can slowly change from a liquid into a gas that is invisible to the naked eye. The gas or “vapors” that are released will start to fill a room if mercury is spilled indoors. MERCURY EXPOSURE Mercury is a very toxic or poisonous substance that people can be exposed to in several ways. If it is swallowed, like from a broken thermometer, it mostly passes through your body and very little is absorbed. If you touch it, a small amount may pass through your skin, but not usually enough to harm you. Mercury is most harmful when you breathe in the vapors that are released when a container is open or a spill occurs. HEALTH EFFECTS Pregnant women, infants and young children are particularly sensitive to the harmful effects of mercury. The health effects that can result from mercury exposure depend on how much mercury you are exposed to and how long you are exposed. Some of the acute effects, ones that may come soon after exposure to high concentrations of mercury are: • Headaches, chills, fever • chest tightness, coughs • hand tremors • nausea, vomiting, abdominal cramps, diarrhea Some effects that may result from chronic, or longer term exposure to mercury vapor can be: • Personality changes • Decreased vision or hearing • Peripheral nerve damage • Elevated blood pressure Children are especially sensitive to mercury and at risk of developing a condition known as acrodynia or “Pinks Disease” by breathing vapors or other exposure circumstances. -

Elemental Mercury Emission in the Indoor Environment Due to Broken Compact Fluorescent Light (CFL) Bulbs
Elemental Mercury Emission In The Indoor Environment Due To Broken Compact Fluorescent Light (CFL) Bulbs David Marr1, Mark Mason1, Stanley Durkee2 1U.S. EPA, RTP, NC 2U.S. EPA, Washington DC Mark Mason l [email protected] l 919-541-4835 Paper control number 553 Introduction Mercury emissions from broken Broken CFL Bulb Cleanup fluorescent bulbs Compact fluorescent light (CFL) bulbs require elemental The U.S EPA, as part of its public outreach program, provides mercury for operation. Each bulb contains a few milligrams Published research on mercury emissions cleanup guidance when a CFL is broken in the indoor of mercury, a value that has been decreasing over time due to environment. As part of this guidance, it is recommended that new technologies and methodologies, driven primarily by from lighting the debris be cleaned up following 5 to 10 minutes of increased environmental and consumer concerns. If a CFL breaks, Aucott et al. (2003) generated mercury emission rate ventilation and some initial steps. Figure 3 shows indoor model some of the mercury is immediately released as elemental equations for fluorescent lamps (FLs) broken in a barrel at results that include the emission rate of Equation 1, but with mercury vapor while the remainder is available for emission three ambient air temperatures in an effort to quantify source removal occurring at 15 minutes to provide a visual of over time to air via the bulb debris and contaminated indoor mercury emissions in time. Equation 1 is their published the impact of proper cleanup on indoor mercury concentrations surfaces until properly remediated. -

Mercury Use and Loss from Gold Mining in Nineteenth-Century Victoria 45
CSIRO Publishing The Royal Society of Victoria, 127, 44 –54, 2015 www.publish.csiro.au/journals/rs 10.1071/RS15017 Me RCuRy uSe and LOSS fROM GOLd MInInG In nIneTeenTh- CenTuRy Victoria Peter Davies1, susan Lawrence2 anD JoDi turnbuLL3 1, 2, 3 department of archaeology and history, La Trobe university, Bundoora, Victoria 3086 Correspondence: Peter davies, [email protected] ABSTRACT: This paper reports on preliminary research into gold-mining-related mercury contamination in nineteenth-century Victoria. data drawn from contemporary sources, including Mineral Statistics of Victoria and Mining Surveyors Reports from 1868‒1888, are used to calculate quantities of mercury used by miners to amalgamate gold in stamp batteries and the rates of mercury lost in the process. Some of the mercury discharged from mining and ore milling flowed into nearby waterways and some remained in the waste residue, the tailings near the mills. We estimate that a minimum of 121 tons of mercury were discharged from stamp batteries in this period. although the figures fluctuate through time and space, they allow a good estimate of how much mercury was leaving the mine workings and entering Victorian creeks and rivers. Better understanding of historic mercury loss can provide the basis for improved mapping of mercury distribution in modern waterways, which can in turn inform the management of catchment systems. Keywords: mercury, gold mining, pollution, water, rivers In recent years, mercury in waterways has emerged as an et al. 1996) and new Zealand (Moreno et al. 2005), while important environmental issue in south-eastern australia extensive mercury pollution also resulted from silver and in many other areas. -

Mercury and Mercury Compounds
United States Office of Air Quality EPA-454/R-97-012 Environmental Protection Planning And Standards Agency Research Triangle Park, NC 27711 December 1997 AIR EPA LOCATING AND ESTIMATING AIR EMISSIONS FROM SOURCES OF MERCURY AND MERCURY COMPOUNDS L & E EPA-454/R-97-012 Locating And Estimating Air Emissions From Sources of Mercury and Mercury Compounds Office of Air Quality Planning and Standards Office of Air and Radiation U.S. Environmental Protection Agency Research Triangle Park, NC 27711 December 1997 This report has been reviewed by the Office of Air Quality Planning and Standards, U.S. Environmental Protection Agency, and has been approved for publication. Mention of trade names and commercial products does not constitute endorsement or recommendation for use. EPA-454/R-97-012 TABLE OF CONTENTS Section Page EXECUTIVE SUMMARY ................................................ xi 1.0 PURPOSE OF DOCUMENT .............................................. 1-1 2.0 OVERVIEW OF DOCUMENT CONTENTS ................................. 2-1 3.0 BACKGROUND ........................................................ 3-1 3.1 NATURE OF THE POLLUTANT ..................................... 3-1 3.2 OVERVIEW OF PRODUCTION, USE, AND EMISSIONS ................. 3-1 3.2.1 Production .................................................. 3-1 3.2.2 End-Use .................................................... 3-3 3.2.3 Emissions ................................................... 3-6 4.0 EMISSIONS FROM MERCURY PRODUCTION ............................. 4-1 4.1 PRIMARY MERCURY -

Direct Detection of Atmospheric Atomic Bromine Leading to Mercury and Ozone Depletion
Direct detection of atmospheric atomic bromine leading to mercury and ozone depletion Siyuan Wanga,1, Stephen M. McNamaraa, Christopher W. Mooreb,2, Daniel Obristb,3, Alexandra Steffenc, Paul B. Shepsond,e,f,4, Ralf M. Staeblerc, Angela R. W. Rasod, and Kerri A. Pratta,g,5 aDepartment of Chemistry, University of Michigan, Ann Arbor, MI 48109; bDivision of Atmospheric Science, Desert Research Institute, Reno, NV 89523; cAir Quality Processes Research Section, Environment and Climate Change Canada, Toronto, ON M3H5T4, Canada; dDepartment of Chemistry, Purdue University, West Lafayette, IN 47907; eDepartment of Earth, Atmospheric, and Planetary Sciences, Purdue University, West Lafayette, IN 47907; fPurdue Climate Change Research Center, Purdue University, West Lafayette, IN 47907; and gDepartment of Earth and Environmental Sciences, University of Michigan, Ann Arbor, MI 48109 Edited by Mark H. Thiemens, University of California San Diego, La Jolla, CA, and approved May 29, 2019 (received for review January 12, 2019) Bromine atoms play a central role in atmospheric reactive halogen O3 producing BrO ([R2]), which can undergo photolysis to chemistry, depleting ozone and elemental mercury, thereby reform Br ([R3]). Br is also regenerated by BrO reaction with enhancing deposition of toxic mercury, particularly in the Arctic NO ([R4]), or a halogen monoxide (XO = BrO, ClO, or IO; near-surface troposphere. However, direct bromine atom mea- [R5]) (19). surements have been missing to date, due to the lack of analytical capability with sufficient sensitivity for ambient measurements. Br2 + hv → Br + Br, [R1] Here we present direct atmospheric bromine atom measurements, conducted in the springtime Arctic. Measured bromine atom levels − Br + O → BrO + O , [R2] reached 14 parts per trillion (ppt, pmol mol 1;4.2× 108 atoms 3 2 − per cm 3) and were up to 3–10 times higher than estimates using + + → + [R3] previous indirect measurements not considering the critical role of BrO hv O2 Br O3, molecular bromine. -

Lead, Mercury and Cadmium in Fish and Shellfish from the Indian Ocean and Red
Journal of Marine Science and Engineering Review Lead, Mercury and Cadmium in Fish and Shellfish from the Indian Ocean and Red Sea (African Countries): Public Health Challenges Isidro José Tamele 1,2,3,* and Patricia Vázquez Loureiro 4 1 Department of Chemistry, Faculty of Sciences, Eduardo Mondlane University, Av. Julius Nyerere, n 3453, Campus Principal, Maputo 257, Mozambique 2 Institute of Biomedical Science Abel Salazar, University of Porto, R. Jorge de Viterbo Ferreira 228, 4050-313 Porto, Portugal 3 CIIMAR/CIMAR—Interdisciplinary Center of Marine and Environmental Research, University of Porto, Terminal de Cruzeiros do Porto, Avenida General Norton de Matos, 4450-238 Matosinhos, Portugal 4 Department of Analytical Chemistry, Nutrition and Food Science, Faculty of Pharmacy, University of Santiago de Compostela, Santiago de Compostela, 15782 A Coruña, Spain; [email protected] * Correspondence: [email protected] Received: 20 March 2020; Accepted: 8 May 2020; Published: 12 May 2020 Abstract: The main aim of this review was to assess the incidence of Pb, Hg and Cd in seafood from African countries on the Indian and the Red Sea coasts and the level of their monitoring and control, where the direct consumption of seafood without quality control are frequently due to the poverty in many African countries. Some seafood from African Indian and the Red Sea coasts such as mollusks and fishes have presented Cd, Pb and Hg concentrations higher than permitted limit by FAOUN/EU regulations, indicating a possible threat to public health. Thus, the operationalization of the heavy metals (HM) monitoring and control is strongly recommended since these countries have laboratories with minimal conditions for HM analysis. -

America's Biggest Mercury Polluters
America’s Biggest Mercury Polluters How Cleaning Up the Dirtiest Power Plants Will Protect Public Health America’s Biggest Mercury Polluters How Cleaning Up the Dirtiest Power Plants Will Protect Public Health Environment America Research & Policy Center by Travis Madsen, Frontier Group Lauren Randall, Environment America Research & Policy Center November 2011 Acknowledgments The authors thank Ann Weeks at Clean Air Task Force and Stephanie Maddin at Earthjustice for providing useful feedback and insightful suggestions on drafts of this report. Nathan Willcox at Environment America Research & Policy Center; Tony Dutzik, Benjamin Davis and Jordan Schneider at Frontier Group; and Meredith Medoway provided editorial support. Environment America Research & Policy Center is grateful to the New York Community Trust for making this report possible. The authors bear responsibility for any factual errors. The views expressed in this report are those of the authors and do not necessarily reflect the views of our funders or those who provided review. © 2011 Environment America Research & Policy Center Environment America Research & Policy Center is a 501(c)(3) organization. We are dedicated to protecting America’s air, water and open spaces. We investigate problems, craft solutions, educate the public and decision makers, and help Americans make their voices heard in local, state and national debates over the quality of our environment and our lives. For more information about Environment America Research & Policy Center or for additional copies of this report, please visit www.environmentamerica.org/center. Frontier Group conducts independent research and policy analysis to support a cleaner, healthier and more democratic society. Our mission is to inject accurate information and compelling ideas into public policy debates at the local, state and federal levels. -

Methylmercury Contamination: Impacts on Aquatic Systems and Terrestrial Species, and Insights for Abatement
Methylmercury Contamination: Impacts on Aquatic Systems and Terrestrial Species, and Insights for Abatement Charles E. Sams USDA Forest Service, Eastern Region Air Quality Program, Milwaukee, Wisconsin Methylmercury (MeHg) is one of the most widespread waterborne contaminants, and through biomagnification processes has commonly been found in prey fish at concentrations toxic to piscivorous birds and mammals. In USEPA’s National Fish Tissue Survey, the Lowest Adverse Effect Concentration of 0.1 g/g wet weight was exceeded in 28% of total samples and 86% of predatory fish samples (USEPA 2002). Evidence suggests that more than a quarter of all mature fish contain methylmercury concentrations above this level. This review focuses on the leading anthropogenic sources of mercury to aquatic systems, through atmospheric deposition and the environmental dynamics of the mercury methylation process in aquatic sediments. The results of extensive mercury monitoring studies are discussed, as well as the reproductive and behavioral impacts on birds and mammals feeding on fish exhibiting realistic contaminant concentrations. Recommendations are provided for continued research and the abatement of methylmercury concentrations in fish through forest management practices. Keywords: mercury deposition, methylmercury, sulfate reducing bacteria, aquatic sediments INTRODUCTION conterminous United States, over 20.2 million ha (50 million acres) were determined to be forested wetlands, Methylmercury (MeHg) is one of the most widespread as well as 10.0 million ha (25 million acres) of emergent waterborne contaminants (USGS 2001a; UNEP 2002; wetlands and 7.3 million ha (18 million acres) of shrub USDHHS and USEPA 2004). Unhealthful levels of MeHg wetlands (Dahl 2000). While National Forest lands in fish have led to the issuance of fish consumption represent only eight percent of the contiguous United advisories by at least 46 states (USEPA 2004). -
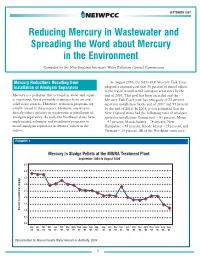
Reducing Mercury in Wastewater and Spreading the Word About Mercury in the Environment
SEPTEMBER 2007 Reducing Mercury in Wastewater and Spreading the Word about Mercury in the Environment Compiled by the New England Interstate Water Pollution Control Commission Mercury Reductions Resulting from In August 2003, the NEG-ECP Mercury Task Force Installation of Amalgam Separators adopted a regional goal that 50 percent of dental offices in the region would install amalgam separators by the Mercury is a pollutant that is found in water and aquat- end of 2005. This goal has been exceeded and the ic organisms, but it primarily originates from air and Mercury Task Force now has new goals of 75 percent solid waste sources. Therefore, reduction programs are separator installation by the end of 2007 and 95 percent usually aimed at these sectors. However, one way to by the end of 2010. In 2005, it was estimated that the directly reduce mercury in wastewater is installation of New England states had the following rates of amalgam amalgam separators. As such, the Northeast states have separator installation: Connecticut – 65 percent, Maine implemented voluntary and mandatory programs to – 95 percent, Massachusetts – 74 percent, New install amalgam separators in dentists’ offices in the Hampshire – 95 percent, Rhode Island – 25 percent, and region. Vermont – 15 percent. All of the Northeast states now FIGURE 1 Mercury in Sludge Pellets at the MWRA Treatment Plant September 2004 to August 2006 4.5 4.0 3.5 3.0 2.5 2.0 1.5 Mercury Concentration (mg/kg) 1.0 0.5 0.0 Sep Oct Nov Dec Jan Feb Mar April May June July Aug Sep Oct Nov Dec Jan Feb Mar April May June July Aug '04 '04 '04 '04 '05 '05 '05 '05 '05 '05 '05 '05 '05 '05 '05 '05 '06 '06 '06 '06 '06 '06 '06 '06 Data provided by Massachusetts Water Resources Authority, 2006 1 Reducing Mercury in Wastewater and Spreading the Word about Mercury in the Environment have legislation or regulations that require installation of results prior to and following installation of amalgam amalgam separators.