Scaling of Multimillion-Atom Biological Molecular Dynamics Simulation on a Petascale Supercomputer
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Web-Based 3D Molecular Structure Editor and Visualizer Platform
Mohebifar and Sajadi J Cheminform (2015) 7:56 DOI 10.1186/s13321-015-0101-7 SOFTWARE Open Access Chemozart: a web‑based 3D molecular structure editor and visualizer platform Mohamad Mohebifar* and Fatemehsadat Sajadi Abstract Background: Chemozart is a 3D Molecule editor and visualizer built on top of native web components. It offers an easy to access service, user-friendly graphical interface and modular design. It is a client centric web application which communicates with the server via a representational state transfer style web service. Both client-side and server-side application are written in JavaScript. A combination of JavaScript and HTML is used to draw three-dimen- sional structures of molecules. Results: With the help of WebGL, three-dimensional visualization tool is provided. Using CSS3 and HTML5, a user- friendly interface is composed. More than 30 packages are used to compose this application which adds enough flex- ibility to it to be extended. Molecule structures can be drawn on all types of platforms and is compatible with mobile devices. No installation is required in order to use this application and it can be accessed through the internet. This application can be extended on both server-side and client-side by implementing modules in JavaScript. Molecular compounds are drawn on the HTML5 Canvas element using WebGL context. Conclusions: Chemozart is a chemical platform which is powerful, flexible, and easy to access. It provides an online web-based tool used for chemical visualization along with result oriented optimization for cloud based API (applica- tion programming interface). JavaScript libraries which allow creation of web pages containing interactive three- dimensional molecular structures has also been made available. -

Water and Salt at the Lipid-Solvent Interface
University of South Florida Scholar Commons Graduate Theses and Dissertations Graduate School April 2019 Water and Salt at the Lipid-Solvent Interface James M. Kruczek University of South Florida, [email protected] Follow this and additional works at: https://scholarcommons.usf.edu/etd Part of the Physics Commons Scholar Commons Citation Kruczek, James M., "Water and Salt at the Lipid-Solvent Interface" (2019). Graduate Theses and Dissertations. https://scholarcommons.usf.edu/etd/8380 This Dissertation is brought to you for free and open access by the Graduate School at Scholar Commons. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. Water and Salt at the Lipid-Solvent Interface by James M. Kruczek A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Applied Physics Department of Physics College of Arts and Sciences University of South Florida Major Professor: Sagar A. Pandit, Ph.D. Ullah, Ghanim, Ph.D. Robert S. Hoy, Ph.D. Jianjun Pan, Ph.D. Yicheng Tu, Ph.D. Date of Approval: March 26, 2019 Keywords: Lipid Bilayer, Ionic Solvents, Ether Lipids, Molecular Simulations Copyright ⃝c 2018, James M. Kruczek Dedication To my wife Nicole, without whom none of this would be possible. To my father Michael, who labored for his family till his last days. To my family, for all of their support. Acknowledgments The work presented in this document would not be possible without the assistance of many academic professionals. In particular, I would like to acknowledge my major advisor Dr. -

Tracking of Bacterial Metabolism with Azidated Precursors and Click- Chemistry”
Tracking of bacterial metabolism with azidated precursors and click-chemistry Dissertation zur Erlangung des Doktorgrades der Naturwissenschaften vorgelegt beim Fachbereich für Biowissenschaften (15) der Johann Wolfang Goethe Universität in Frankfurt am Main von Alexander J. Pérez aus Nürnberg Frankfurt am Main 2015 Dekanin: Prof. Dr. Meike Piepenbring Gutachter: Prof. Dr. Helge B. Bode Zweitgutachter: Prof. Dr. Joachim W. Engels Datum der Disputation: 2 Danksagung Ich danke meinen Eltern für die stete und vielseitige Unterstützung, deren Umfang ich sehr zu schätzen weiß. Herrn Professor Dr. Helge B. Bode gilt mein besonderer Dank für die Übernahme als Doktorand und für die Gelegenheit meinen Horizont in diesen mich stets faszinierenden Themenbereich in dieser Tiefe erweitern zu lassen. Seine persönliche und fachliche Unterstützung bei der Projektwahl und der entsprechenden Umsetzung ist in dieser Form eine Seltenheit und ich bin mir dieser Tatsache voll bewusst. Gerade die zusätzlich erworbenen Kenntnisse im Bereich der Biologie, sowie der Wert interdisziplinärer Zusammenarbeit ist mir durch zahlreiche freundliche und wertvolle Mitglieder der Arbeitsgruppe bewusst geworden und viele zündenden Ideen wären ohne sie womöglich nie aufgekommen. Einen besonderen Dank möchte ich in diesem Kontext Wolfram Lorenzen und Sebastian Fuchs, die gerade in der Anfangszeit eine große Hilfe waren, ausdrücken. Dies gilt ebenso für die „N100-Crew“ und sämtliche Freunde, die in dieser Zeit zu mir standen und diesen Lebensabschnitt unvergesslich gemacht haben. -
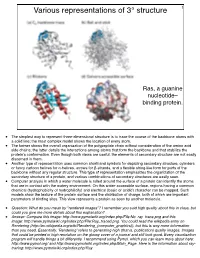
Various Representations of 3° Structure 1
Various representations of 3° structure 1 Ras, a guanine nucleotide– binding protein. • The simplest way to represent three-dimensional structure is to trace the course of the backbone atoms with a solid line; the most complex model shows the location of every atom. • The former shows the overall organization of the polypeptide chain without consideration of the amino acid side chains; the latter details the interactions among atoms that form the backbone and that stabilize the protein’s conformation. Even though both views are useful, the elements of secondary structure are not easily discerned in them. • Another type of representation uses common shorthand symbols for depicting secondary structure, cylinders or fancy cartoon helices for α-helices, arrows for β-strands, and a flexible string-like form for parts of the backbone without any regular structure. This type of representation emphasizes the organization of the secondary structure of a protein, and various combinations of secondary structures are easily seen. • Computer analysis in which a water molecule is rolled around the surface of a protein can identify the atoms that are in contact with the watery environment. On this water-accessible surface, regions having a common chemical (hydrophobicity or hydrophilicity) and electrical (basic or acidic) character can be mapped. Such models show the texture of the protein surface and the distribution of charge, both of which are important parameters of binding sites. This view represents a protein as seen by another molecule. • Question: What do you mean by "rendered images"? I remember you said high quality about this in class, but could you give me more details about this explanation? • Answer: Compare this image: http://www.pymolwiki.org/index.php/File:No_ray_trace.png and this image: http://www.pymolwiki.org/index.php/File:Ray_traced.png. -

Visualizing Protein Structures-Tools and Trends
Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 12 January 2020 Visualizing protein structures - tools and trends 1,2 3 1,2 X. Martinez , M. Chavent , M. Baaden 1) CNRS, Université de Paris, UPR 9080, Laboratoire de Biochimie Théorique, 13 rue Pierre et Marie Curie, F-75005, Paris, France 2) Institut de Biologie Physico-Chimique-Fondation Edmond de Rotschild, PSL Research University, Paris, France 3) Institut de Pharmacologie et de Biologie Structurale IPBS, Université de Toulouse, CNRS, UPS, Toulouse, France Abstract Molecular visualisation is fundamental in the current scientific literature, textbooks and dissemination materials, forming an essential support for presenting results, reasoning on and formulating hypotheses related to molecular structure. Visual exploration has become easily accessible on a broad variety of platforms thanks to advanced software tools that render a great service to the scientific community. These tools are often developed across disciplines bridging computer science, biology and chemistry. Here we first describe a few Swiss Army knives geared towards protein visualisation for everyday use with an existing large user base, then focus on more specialised tools for peculiar needs that are not yet as broadly known. Our selection is by no means exhaustive, but reflects a diverse snapshot of scenarios that we consider informative for the reader. We end with an account of future trends and perspectives. Keywords Molecular Graphics, Protein visualization, Software tools, Virtual reality Introduction Many parts of science rely on a visualization-driven cycle of experimentation, reasoning, conjecture and validation, even more so in relation with structural biology and biophysics. Molecular visualization (1) in particular is now broadly used in many contexts, with the purpose of illustration in the scientific literature or the aim to gain insight about primary research data. -

Engine for Molecule Visualization in a Web Browser
MASARYKOVA UNIVERZITA FAKULTA}w¡¢£¤¥¦§¨ INFORMATIKY !"#$%&'()+,-./012345<yA| Engine for Molecule Visualization in a Web Browser MASTER’S THESIS Jaromír Svoboda Brno, spring 2014 Declaration Hereby I declare, that this paper is my original authorial work, which I have worked out by my own. All sources, references and literature used or excerpted during elaboration of this work are properly cited and listed in complete reference to the due source. Jaromír Svoboda Advisor: RNDr. David Sehnal ii Acknowledgement I would like to thank my supervisor RNDr. David Sehnal for patient guidance and informed advice throughout writing this thesis. iii Abstract The main focus of this master’s thesis is the design and implementa- tion of lightweight molecular visualization engine (called LiveMol) in form of a JavaScript library. The engine utilizes widely adopted WebGL API to display GPU-accelerated graphics in web browsers. Due to the size of complex protein molecules, the primary goal is high performance. Furthermore, the design of LiveMol enables users to extend the core functionality by simply defining custom coloring schemes of molecule models or implement completely new visual- ization modes. iv Keywords molecular visualization, protein, secondary structure, WebGL, LiveMol v Contents I INTRODUCTION 1 1 Introduction ............................2 II CURRENT DEVELOPMENTS 3 2 Current Molecular Visualization Software ..........4 2.1 Desktop Applications ....................4 2.1.1 Visual Molecular Dynamic . .4 2.1.2 PyMOL . .4 2.1.3 RasMol/OpenRasMol . .5 2.1.4 BALL/BALLView . .5 2.1.5 Gabedit . .5 2.1.6 QuteMol . .5 2.1.7 Avogadro . .6 2.2 JavaScript-based Web Applications ............6 2.2.1 Jmol/JSmol . -

Illustrative Molecular Visualization with Continuous Abstraction Matthew Van Der Zwan, Wouter Lueks, Henk Bekker, Tobias Isenberg
Illustrative Molecular Visualization with Continuous Abstraction Matthew van der Zwan, Wouter Lueks, Henk Bekker, Tobias Isenberg To cite this version: Matthew van der Zwan, Wouter Lueks, Henk Bekker, Tobias Isenberg. Illustrative Molecular Visu- alization with Continuous Abstraction. Computer Graphics Forum, Wiley, 2011, 30 (3), pp.683-690. 10.1111/j.1467-8659.2011.01917.x. hal-00781508 HAL Id: hal-00781508 https://hal.inria.fr/hal-00781508 Submitted on 27 Jan 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Public Domain Eurographics / IEEE Symposium on Visualization 2011 (EuroVis 2011) Volume 30 (2011), Number 3 H. Hauser, H. Pfister, and J. J. van Wijk (Guest Editors) Illustrative Molecular Visualization with Continuous Abstraction Matthew van der Zwan,1 Wouter Lueks,1 Henk Bekker,1 and Tobias Isenberg1,2 1Johann Bernoulli Institute of Mathematics and Computer Science, University of Groningen, The Netherlands 2DIGITEO in collaboration with VENISE–LIMSI–CNRS and AVIZ–INRIA, Saclay, France Abstract Molecular systems may be visualized with various degrees of structural abstraction, support of spatial perception, and ‘illustrativeness.’In this work we propose and realize methods to create seamless transformations that allow us to affect and change each of these three parameters individually. -

Open Source Molecular Modeling
Accepted Manuscript Title: Open Source Molecular Modeling Author: Somayeh Pirhadi Jocelyn Sunseri David Ryan Koes PII: S1093-3263(16)30118-8 DOI: http://dx.doi.org/doi:10.1016/j.jmgm.2016.07.008 Reference: JMG 6730 To appear in: Journal of Molecular Graphics and Modelling Received date: 4-5-2016 Accepted date: 25-7-2016 Please cite this article as: Somayeh Pirhadi, Jocelyn Sunseri, David Ryan Koes, Open Source Molecular Modeling, <![CDATA[Journal of Molecular Graphics and Modelling]]> (2016), http://dx.doi.org/10.1016/j.jmgm.2016.07.008 This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain. Open Source Molecular Modeling Somayeh Pirhadia, Jocelyn Sunseria, David Ryan Koesa,∗ aDepartment of Computational and Systems Biology, University of Pittsburgh Abstract The success of molecular modeling and computational chemistry efforts are, by definition, de- pendent on quality software applications. Open source software development provides many advantages to users of modeling applications, not the least of which is that the software is free and completely extendable. In this review we categorize, enumerate, and describe available open source software packages for molecular modeling and computational chemistry. 1. Introduction What is Open Source? Free and open source software (FOSS) is software that is both considered \free software," as defined by the Free Software Foundation (http://fsf.org) and \open source," as defined by the Open Source Initiative (http://opensource.org). -

A Virtual Alternative to Molecular Model Sets
Phankingthongkum and Limpanuparb BMC Res Notes (2021) 14:66 BMC Research Notes https://doi.org/10.1186/s13104-021-05461-7 RESEARCH NOTE Open Access A virtual alternative to molecular model sets: a beginners’ guide to constructing and visualizing molecules in open-source molecular graphics software Siripreeya Phankingthongkum and Taweetham Limpanuparb* Abstract Objective: The application of molecular graphics software as a simple and free alternative to molecular model sets for introductory-level chemistry learners is presented. Results: Based on either Avogadro or IQmol, we proposed four sets of tasks for students, building basic molecular geometries, visualizing orbitals and densities, predicting polarity of molecules and matching 3D structures with bond- line structures. These topics are typically covered in general chemistry for frst-year undergraduate students. Detailed step-by-step procedures are provided for all tasks for both programs so that instructors and students can adopt one of the two programs in their teaching and learning as an alternative to molecular model sets. Keywords: Chemical education, Molecular model, General chemistry, Molecular graphics software Introduction at high price. With open-source licensing, the cost and Te use of molecular model has been recommended to availability of the software is no longer an issue. be part of the curriculum to enhance spatial thinking in Most molecular graphics programs allow users to con- students of chemistry [1]. Physical molecular model sets struct, edit and visualize molecules in 3D, and hence, are are usually employed in an introductory-level chemistry viable alternatives to conventional teaching materials. laboratory [2]. Other similar teaching tools [3–45] vary Te issue here is therefore how to bring these dynamic greatly in terms of cost, ease of use, required amount of and interactive visualization programs as scafolding time and suitability for relevant topics in chemistry. -

Ballview a Molecular Viewer and Modeling Tool
BALLView A molecular viewer and modeling tool Dissertation zur Erlangung des Grades des Doktors der Ingenieurwissenschaften der Naturwissenschaftlich– Technischen Fakultäten der Universität des Saarlandes vorgelegt von Diplom-Biologe Andreas Moll Saarbrücken im Mai 2007 Tag des Kolloquiums: 18. Juli 2007 Dekan: Prof. Dr. Thorsten Herfet Mitglieder des Prüfungsausschusses: Prof. Dr. Philipp Slusallek Prof. Dr. Hans-Peter Lenhof Prof. Dr. Oliver Kohlbacher Dr. Dirk Neumann Acknowledgments The work on this thesis was carried out during the years 2002-2007 at the Center for Bioinformatics in the group of Prof. Dr. Hans-Peter Lenhof who also was the supervisor of the thesis. With his deeply interesting lecture on bioinformatics, Prof. Dr. Hans-Peter Lenhof kindled my interest in this field and gave me the freedom to do research in those areas that fascinated me most. The implementation of BALLView would have been unthinkable without the help of all the people who contributed code and ideas. In particular, I want to thank Prof. Dr. Oliver Kohlbacher for his splendid work on the BALL library, on which this thesis is based on. Furthermore, Prof. Kohlbacher had at any time an open ear for my questions. Next I want to thank Dr. Andreas Hildebrandt, who had good advices for the majority of problems that I was confronted with. In addition he contributed code for database access, field line calculations, spline points calculations, 2D depiction of molecules, and for the docking in- terface. Heiko Klein wrote the precursor of the VIEW library. Anne Dehof implemented the peptide builder, the secondary structure assignment, and a first version of the editing mo- de. -

ETP) User Guide
Electron Tunneling in Proteins Program (ETP) User Guide Version 1.0 University of California, Davis One Shields Ave, Davis, CA 95616 1 ETP Program License Copyright © 2016 The Regents of the University of California, Davis campus. All Rights Reserved. Redistribution and use in source and binary forms, with or without modification, are permitted by nonprofit, research institutions for research use only, provided that the following conditions are met: Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution. The name of The Regents may not be used to endorse or promote products derived from this software without specific prior written permission. The end-user understands that the program was developed for research purposes and is advised not to rely exclusively on the program for any reason. THE SOFTWARE PROVIDED IS ON AN "AS IS" BASIS, AND THE REGENTS HAVE NO OBLIGATION TO PROVIDE MAINTENANCE, SUPPORT, UPDATES, ENHANCEMENTS, OR MODIFICATIONS. THE REGENTS SPECIFICALLY DISCLAIM ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE REGENTS BE LIABLE TO ANY PARTY FOR DIRECT, INDIRECT, SPECIAL, INCIDENTAL, EXEMPLARY OR CONSEQUENTIAL DAMAGES, INCLUDING BUT NOT LIMITED TO PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES, LOSS OF USE, DATA OR PROFITS, OR BUSINESS INTERRUPTION, HOWEVER CAUSED AND UNDER ANY THEORY OF LIABILITY WHETHER IN CONTRACT, STRICT LIABILITY OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE AND ITS DOCUMENTATION, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE. -
Free and Open Source Software
Free and open source software Copyleft ·Events and Awards ·Free software ·Free Software Definition ·Gratis versus General Libre ·List of free and open source software packages ·Open-source software Operating system AROS ·BSD ·Darwin ·FreeDOS ·GNU ·Haiku ·Inferno ·Linux ·Mach ·MINIX ·OpenSolaris ·Sym families bian ·Plan 9 ·ReactOS Eclipse ·Free Development Pascal ·GCC ·Java ·LLVM ·Lua ·NetBeans ·Open64 ·Perl ·PHP ·Python ·ROSE ·Ruby ·Tcl History GNU ·Haiku ·Linux ·Mozilla (Application Suite ·Firefox ·Thunderbird ) Apache Software Foundation ·Blender Foundation ·Eclipse Foundation ·freedesktop.org ·Free Software Foundation (Europe ·India ·Latin America ) ·FSMI ·GNOME Foundation ·GNU Project ·Google Code ·KDE e.V. ·Linux Organizations Foundation ·Mozilla Foundation ·Open Source Geospatial Foundation ·Open Source Initiative ·SourceForge ·Symbian Foundation ·Xiph.Org Foundation ·XMPP Standards Foundation ·X.Org Foundation Apache ·Artistic ·BSD ·GNU GPL ·GNU LGPL ·ISC ·MIT ·MPL ·Ms-PL/RL ·zlib ·FSF approved Licences licenses License standards Open Source Definition ·The Free Software Definition ·Debian Free Software Guidelines Binary blob ·Digital rights management ·Graphics hardware compatibility ·License proliferation ·Mozilla software rebranding ·Proprietary software ·SCO-Linux Challenges controversies ·Security ·Software patents ·Hardware restrictions ·Trusted Computing ·Viral license Alternative terms ·Community ·Linux distribution ·Forking ·Movement ·Microsoft Open Other topics Specification Promise ·Revolution OS ·Comparison with closed