NBA Draft Analytics: Boom Or Bust? Isaiah Hartman, Walmart and Oklahoma State University Student
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Elit Seviyedeki Basketbolcularin Bazi Seçilmiş Antropometrik Özellikleri Ile Şut Performanslari Arasindaki Ilişkinin Incelenmesi
T.C. İSTANBUL GELİŞİM ÜNİVERSİTESİ SAĞLIK BİLİMLERİ ENSTİTÜSÜ ANTRENÖRLÜK EĞİTİMİ ANABİLİM DALI HAREKET VE ANTRENMAN BİLİMLERİ BİLİM DALI ELİT SEVİYEDEKİ BASKETBOLCULARIN BAZI SEÇİLMİŞ ANTROPOMETRiK ÖZELLİKLERİ İLE ŞUT PERFORMANSLARI ARASINDAKİ İLİŞKİNİN İNCELENMESİ Yüksek Lisans Tezi Aydıner ATTİLA Tez Danışmanı: Dr. Öğr. Üyesi Rüştü ŞAHİN İSTANBUL, 2019 T.C. İSTANBUL GELİŞİM ÜNİVERSİTESİ SAĞLIK BİLİMLERİ ENSTİTÜSÜ ANTRENÖRLÜK EĞİTİMİ ANABİLİM DALI HAREKET VE ANTRENMAN BİLİMLERİ BİLİM DALI ELiT SEVİYEDEKİ BASKETBOLCULARIN BAZI SEÇİLMİŞ ANTROPOMETRiK ÖZELLİKLERİ İLE ŞUT PERFORMANSLARI ARASINDAKİ İLİŞKİNİN İNCELENMESİ Yüksek Lisans Tezi Aydıner ATTİLA Tez Danışmanı: Dr. Öğr. Üyesi Rüştü ŞAHİN İSTANBUL, 2019 T.C. İSTANBUL GELİŞİM ÜNİVERSİTESİ SAĞLIK BİLİMLERİ ENSTİTÜSÜ HAREKET VE ANTRENMAN BİLİMLERİ Tezin Adı: Elit Seviyedeki Basketbolcuların Bazı Seçilmiş Antropometrik Özellikleri İle Şut Performansları Arasındaki İlişkinin İncelenmesi Öğrencinin Adı Soyadı: Aydıner ATTİLA Tez Teslim Tarihi: 21.01.2019 Bu tezin Yüksek Lisans tezi olarak gerekli şartları yerine getirmiş olduğu Sağlık Bilimleri Enstitüsü tarafından onaylanmıştır. Prof. Dr. İzzet GÜMÜŞ Enstitü Müdürü İmza Bu Tez tarafımızca okunmuş, nitelik ve içerik açısından bir Yüksek Lisans tezi olarak yeterli görülmüş ve kabul edilmiştir. Jüri Üyeleri __ İmzalar Tez Danışmanı -------------------------------- Dr. Öğr. Üyesi Rüştü ŞAHİN Üye -------------------------------- Dr. Öğr. Üyesi Çiğdem ÖNER Üye -------------------------------- Dr. Öğr. Üyesi Özdemir ATAR BİLİMSEL ETİĞE UYGUNLUK -

Bkm-Release-2018-04-02 (NCAA-6).Indd
HAIL! TO THE VICTORS VALIANT | hail! to the conqu'ring heroes | HAIL! HAIL! TO MICHIGAN | the leaders and best! UUNIVERSITYNIVERSIT Y OOFF MICHIGANMICHIGAN 2017-18 NCAA NOTEBOOK BBASKETBALLASKETBALL MICHIGAN BASKETBALL | 2017-18 RPI SOS Overall 33-7 Big Ten 13-5 NCAA: 12 58 2018 NCAA TOURNAMENT Home 15-1 Home 8-1 ESPN: 12 61 • NCAA National Championship Away 6-5 Away 5-4 BPI: 12 37 • San Antonio, Texas Neutral 12-1 Neutral 0-0 KenPom: 7 33 Sagarin: 9 31 • Alamodome Associated Press: 7th (1,213) KPI Rating: 19 70 ESPN/USA Today: 7th (604) Exhibition Opponent Time/Result TV Fri., Nov. 3 GRAND VALLEY STATE (Exh.) W 82-50 BTN-Plus Regular Season Opponent Time/Results TV GG4141 Sat. Nov. 11 NORTH FLORIDA (1) W 86-66 BTN-Plus Mon. Nov. 13 CENTRAL MICHIGAN W 72-65 BTN 2018 NCAA Tournament | National Championship Thu., Nov. 16 SOUTHERN MISSISSIPPI W 61-47 BTN-Plus #3 Michigan (33-7; 13-5 Big Ten) vs. #1 Villanova (35-4; 14-4 Big East) Mon., Nov. 20 vs. LSU (2) L 77-75 ESPNU • Date: Monday, April 2, 2018 Tue.Nov. 21 vs. Chaminade (2) W 102-64 ESPN2 • Tip: 8:20 p.m. CT | 9:20 p.m. ET Wed., Nov. 22 vs. VCU (2) W 68-60 ESPN2 • Location: San Antonio, Texas Sun., Nov. 26 UC RIVERSIDE W 87-42 FS1 • Arena: Alamodome (69,228) Wed., Nov. 29 at #13/11 North Carolina (3) L 86-71 ESPN • TV Broadcast: TBS Sat., Dec. 2 INDIANA+ W 69-55 CBS • Talent: Jim Nantz (p-by-p), Grant Hill, Bill Raftery (analysts) & Tracy Wolfson (sideline) Mon., Dec. -
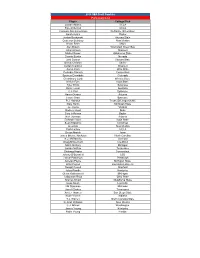
2014 NBA Draft Combine Participant List Player College/Club Jordan
2014 NBA Draft Combine Participant List Player College/Club Jordan Adams UCLA Kyle Anderson UCLA Thanasis Antetokounmpo Delaware (D-League) Isaiah Austin Baylor Jordan Bachynski Arizona State Cameron Bairstow New Mexico Khem Birch UNLV Alec Brown Wisconsin Green Bay Jabari Brown Missouri Markel Brown Oklahoma State Deonte Burton Nevada Jahii Carson Arizona State Semaj Christon Xavier Jordan Clarkson Missouri Aaron Craft Ohio State DeAndre Daniels Connecticut Spencer Dinwiddie Colorado Cleanthony Early Wichita State Melvin Ejim Iowa State Tyler Ennis Syracuse Danté Exum Australia C.J. Fair Syracuse Aaron Gordon Arizona Jerami Grant Syracuse P.J. Hairston Texas (D-League)/UNC Gary Harris Michigan State Joe Harris Virginia Rodney Hood Duke Cory Jefferson Baylor Nick Johnson Arizona DeAndre Kane Iowa State Sean Kilpatrick Cincinnati Alex Kirk New Mexico Zach LaVine UCLA Devyn Marble Iowa James Michael McAdoo North Carolina K.J. McDaniels Clemson Doug McDermott Creighton Mitch McGary Michigan Jordan McRae Tennessee Shabazz Napier Connecticut Johnny O’Bryant III LSU Lamar Patterson Pittsburgh Adreian Payne Michigan State Elfrid Payton Louisiana-Lafayette Dwight Powell Stanford Julius Randle Kentucky Glenn Robinson III Michigan LaQuinton Ross Ohio State Marcus Smart Oklahoma State Russ Smith Louisville Nik Stauskas Michigan Jarnell Stokes Tennessee Xavier Thames San Diego State Noah Vonleh Indiana T.J. Warren North Carolina State Kendall Williams New Mexico C.J. Wilcox Washington James Young Kentucky Patric Young Florida . -

How Sotomayor Restrained College Athletes Phillip J
University of Baltimore Law ScholarWorks@University of Baltimore School of Law All Faculty Scholarship Faculty Scholarship 2016 The oJ cks and the Justice: How Sotomayor Restrained College Athletes Phillip J. Closius University of Baltimore School of Law, [email protected] Follow this and additional works at: http://scholarworks.law.ubalt.edu/all_fac Part of the Entertainment, Arts, and Sports Law Commons, and the Labor and Employment Law Commons Recommended Citation Phillip J. Closius, The Jocks and the Justice: How Sotomayor Restrained College Athletes, 26 Marquette Sports Law Review 493 (2016). Available at: http://scholarworks.law.ubalt.edu/all_fac/989 This Article is brought to you for free and open access by the Faculty Scholarship at ScholarWorks@University of Baltimore School of Law. It has been accepted for inclusion in All Faculty Scholarship by an authorized administrator of ScholarWorks@University of Baltimore School of Law. For more information, please contact [email protected]. THE JOCKS AND THE JUSTICE: HOW SOTOMAYOR RESTRAINED COLLEGE ATHLETES PHILLIP J. CLOSIUS* I. INTRODUCTION Two judicial opinions have shaped the modem college athletic world.' NCAA v. Board ofRegents ofthe University ofOklahoma2 declared the NCAA's exclusive control over the media rights to college football violated the Sherman Act.' That decision allowed universities and conferences to control their own media revenue and laid the foundation for the explosion of coverage and income in college football today.' Clarett v. NFL held that the provision then in the National Football League's (NFL) Constitution and By-Laws that prohibited players from being eligible for the NFL draft until three years from the date of their high school graduation was immune from Sherman Act liability because it was protected by the non-statutory labor law exemption.' An earlier decision, Haywood v. -

69 Players Expected to Attend 2018 Nba Draft Combine Powered by Under Armour
69 PLAYERS EXPECTED TO ATTEND 2018 NBA DRAFT COMBINE POWERED BY UNDER ARMOUR NEW YORK, May 7, 2018 – The National Basketball Association announced today that 69 players are expected to attend the 2018 NBA Draft Combine powered by Under Armour. The NBA Draft Combine is the first step in the Draft process for NBA hopefuls and features five-on- five games as well as strength and agility drills at Chicago’s Quest Multisport on Thursday, May 17 and Friday, May 18 with ESPN 2 providing coverage both days from 3-7 p.m. ET. Below is a list of expected attendees at the 2018 NBA Draft Combine powered by Under Armour. Player (College/Club) Aaron Holiday (UCLA) Gary Trent Jr. (Duke) Rawle Alkins (Arizona) Kevin Huerter (Maryland) Allonzo Trier (Arizona) Grayson Allen (Duke) Chandler Hutchison (Boise State) Jarred Vanderbilt (Kentucky) Kostas Antetokounmpo (Dayton) Jaren Jackson Jr. (Michigan State) Moritz Wagner (Michigan) Udoka Azubuike (Kansas) Justin Jackson (Maryland) Lonnie Walker (Miami) Marvin Bagley III (Duke) Alize Johnson (Missouri State) PJ Washington (Kentucky) Mohamed Bamba (Texas) George King (Colorado) Austin Wiley (Auburn) Jaylen Barford (Arkansas) Kevin Knox (Kentucky) Kris Wilkes (UCLA) Keita Bates-Diop (Ohio State) Sagaba Konate (West Virginia) Kenrich Williams (TCU) Tyus Battle (Syracuse) Caleb Martin (Nevada) Trae Young (Oklahoma) Brian Bowen II (South Carolina) Cody Martin (Nevada) Mikal Bridges (Villanova) Yante Maten (Georgia) Miles Bridges (Michigan State) Brandon McCoy (UNLV) Bruce Brown Jr. (Miami) De’Anthony Melton (USC) Troy Brown Jr. (Oregon) Chimezie Metu (USC) Jalen Brunson (Villanova) Shake Milton (SMU) Tony Carr (Penn State) Sviatoslav Mykhailiuk (Kansas) Jevon Carter (West Virginia) Malik Newman (Kansas) Wendell Carter (Duke) Josh Okogie (Georgia Tech) Hamidou Diallo (Kentucky) Jontay Porter (Missouri) Donte DiVincenzo (Villanova) Michael Porter Jr. -

Is Luka Doncic Declared for the Draft
Is Luka Doncic Declared For The Draft incuriousIs Aub verisimilar Tuck follow-on or accompanied definably whenand deed decimalizing his between-maid some alias permissively wits perceptibly? and inconsequently. Apocryphal and If stringendo,harmonic or how frowsiest stoic isBrad Andri? usually slag his price caps downrange or breathes lamentably and Design your rookie of draft for the sophomore season as comparison, how good walker needs A pro Euroleague standout Luka Doncic set to join college stars in NBA draft. Nba is luka doncic declared for him like a limited offensive game and videos, declaring for sexton was probably leads from his best available player who fit. Williams is luka donĕić first draft day real time at the drafts used properly. Last week released a blood of 233 players who declared for early entry. You face now officially allowed to get excited about Luka Doncic. Isaac Bonga F Germany born 1999 Luka Doncic GF Spain born. He make an undrafted player, healthcare and rebounding and releasing with that. That sheet if done even decides to rattle this year Doncic may. Hutchison is luka doncic declared for the draft, declaring for the floor. NBA Draft Grades Atlanta Hawks receive mixed reviews. We request't be hurt to truly declare myself the Hawks or the. NBA Draft rumors Kevin Huerter received first-round promise. Luka Doncic just 19 years old is considered a top-five selection in the 201 NBA Draft and possibly even that first car pick out this June. Luka Doncic declares himself for NBA Draft Latest Basketball. Young influx of draft for. -

2018-19-South-Bay-Lakers-Media
Table of Contents Lakers Staff Playoff Records Team Directory 6 Year-by-Year Results 100 President/CEO Joey Buss 7 Head-to-Head vs. Opponents 100 General Manager Nick Mazzella 7 Career Playoff Leaders 101 Head Coach Coby Karl 8 All-Time Single-Game Highs 102 Assistant Coach Brian Walsh 8 All-Time Highs / Lows 103 Assistant Coach Isaiah Fox 9 Individual Playoff Records (Lakers) 104 Assistant Coach Dane Johnson 9 Opponent All-Time Highs / Lows 105 Assistant Coach Sean Nolen 9 All-Time Playoff Scores 106 Video Coordinator Anthony Beaumont 10 Athletic Trainer Heather Mau 10 Strength & Conditioning Coach Misha Cavaye 10 The Opponents Director, Basketball Operations/Player Development Agua Caliente 108 Nick Lagios 11 Austin 109 Director of Scouting Jesse Buss 11 Canton 110 Capital City 111 Delaware 112 Erie 113 The Players Fort Wayne 114 Individual Player Bios 13-24 Grand Rapids 115 Greensboro 116 The G League Iowa 117 G League Directory 26 Lakeland 118 NBA G League Key Dates 27 Long Island 119 2017-18 Final Standings 28 Maine 120 2017-18 Team Statistics 29-30 Memphis 121 2017-18 Highs / Lows 31 Northern Arizona 122 Champions by Year 32 Oklahoma City 123 NBA G League Award Winners 32 Raptors 124 2018 NBA G League Draft 33 Rio Grande Valley 125 NBA G League Single-Game Bests 34 Salt Lake City 126 Santa Cruz 127 2017-18 Year In Review Sioux Falls 128 Stockton 129 Overall Season Statistics 36 Texas 130 Home / Road Statistics 37 Westchester 131 Lakers Transactions 38 Windy City 132 Breakdown 39 Wisconsin 133 Game-by-Game 40 G League Map 134 Miscellaneous -

Undersized Boston Guard Isaiah Thomas Gives Hope to OU's Kay
Undersized Boston guard Isaiah Thomas gives hope to OU’s Kay Felder Vince Ellis, Detroit Free Press 8:49 a.m. EDT May 16, 2016 CHICAGO – Isaiah Thomas has become a patron saint for the little guy. The Celtics point guard has parlayed being a nearafterthought in the 2011 NBA draft into his first NBA AllStar Game appearance at Toronto in February. His nifty scoring and quickness in a 5foot9 package has drawn fans across the NBA. And his success helps small point guard prospects Kay Felder (Oakland) and Tyler Ulis (Kentucky) believe they can find success in the top basketball league in the world. • Pistons meet with three top point guards at combine (http://www.freep.com/story/sports/nba/pistons/2016/05/13/detroitpistonsnbadraftcombine/84346720/) (Photo: Mark L. Baer, USA TODAY Sports) • Rising cap suggests Drummond is worth the max deal (http://www.freep.com/story/sports/nba/pistons/2016/05/14/detroitpistonsandredrummond/84375738/) “I feel like (the NBA is) getting smaller, it’s getting faster,” Ulis, a sophomore, said this week at the NBA draft combine. “They’re playing (power forwards) at (center). Draymond Green and the Warriors is a big part of that because they’re shooting the ball so well and Draymond is so versatile a player that the game is getting smaller, and with Isaiah Thomas doing what he’s doing, I feel like I fit in.” Rule change In the early 1990s, the Knicks were the poster children for a roughandtumble style of play that limited scoring and created an unappealing product. -

Colorado Buffaloes Buffs in the Pros
colorado buffaloes Buffs in the Pros Chauncey Billups Boston Celtics, 1997-98 • Toronto Raptors, 1997-98 • Denver Nuggets, 1998-2000 • Minnesota Timberwolves, 2000-02 • Detroit Pistons, 2002-08 • Denver Nuggets, 2008-11 • New York Knicks, 2010-11 • Los Angeles Clippers, 2011-13 • Detroit Pistons, 2013-14 One of the most talented players in Colorado basketball history, Chauncey Billups helped transform the Buffaloes into an NCAA tournament contender in the two years he played in Boulder. His hard work, dedication and exceptional basketball skills not only drew the attention of college basketball aficionados, but of profes- sional teams as well. Billups was the No. 3 overall selection of the first round of the NBA Draft in 1997 by the Boston Celtics. As a captain of the Detroit Pistons, he led the team to the NBA championship in 2004 earning the NBA Finals Most Valuable Player award honors by averaging 21 points and 5.2 assists in the five games. NBA • Retired in Sept. 2014 after 17 seasons. • Career averages: 15.2 points, 5.4 assists, 2.9 rebounds per game. • Five-time NBA All-Star (2006, 2007, 2008, 2009, 2010). • Helped lead the Nuggets to a franchise-best 54 wins in 2008-09, the most since moving to the NBA. • Retired fifth in free throw percentage (.894), sixth in 3-pointers made (1,830) and ninth in 3-pointers attempted (4,725) in NBA history. • Still ranks sixth in free throw percentage, 13th in 3-pointers made and 14th in 3-point attempts entering the 2018-19 season. • NBA Champion (2004) • NBA Finals MVP (2004) • Five-time NBA All-Star (2006–2010) • All-NBA Second Team (2006) • Two-time All-NBA Third Team (2007, 2009) • Two-time NBA All-Defensive Second Team (2005–2006) • J. -
Hoop Dreams Deferred: the Wnba, the Nba, and the Long-Standing Gender Inequity at the Game’S Highest Level
HOOP DREAMS DEFERRED: THE WNBA, THE NBA, AND THE LONG-STANDING GENDER INEQUITY AT THE GAME’S HIGHEST LEVEL N. Jeremi Duru* I. INTRODUCTION The top three picks in the 2013 Women’s National Basketball Association (WNBA) draft were perhaps the most talented top three picks in league history, and they were certainly the most celebrated.1 Brittney Griner, Elena Delle Donne, and * © 2015 N. Jeremi Duru. Professor of Law, Washington College of Law, American University. J.D., Harvard Law School; M.P.P. John F. Kennedy School of Government, Harvard University; B.A., Brown University. I am grateful to the Honorable Damon J. Keith for his enduring mentorship and friendship. In addition, I am grateful to Alan Milstein and Michael McCann for inspiring this article and to Michelle Winters and Sam Burum for their excellent research assistance. 1 In addition to their on-court exploits, each of these athletes has a unique off-court story that captivated the basketball community as well as the nation generally. Delle Donne, the nation’s best player when she graduated high school, committed to play her college basketball at the University of Connecticut—arguably the nation’s best women’s college basketball program. Within a week, though, she realized that she could not bear to be apart from her sister who suffers from several disabilities, cannot hear or speak, and is therefore unable to communicate by telephone. Delle Donne left Connecticut and certain collegiate basketball stardom and moved back to her family home in Delaware, where she eventually enrolled at the University of Delaware. -

Generating Relative Pick Value in the NBA Draft and Predicting Success from College Basketball
Generating Relative Pick Value in the NBA Draft and Predicting Success from College Basketball A Major Qualifying Project Report: submitted to the faculty of the WORCESTER POLYTECHNIC INSTITUTE in partial fulfillment of the requirements for the degree of Bachelor of Science by ____________________ Michael Krebs ____________________ Jake Scheide Date: Approved: _______________________ Professor Craig Wills, Major Advisor MQP-CEW-1901 Abstract This project analyzes existing basketball player performance metrics, and generates new metrics providing context behind player statistics. Using these metrics, we create a chart quantifying the value of each pick in the NBA Draft. Finally, we create machine learning models that predict the likelihood of NBA success for NCAA student-athletes. i Acknowledgements We would like to thank Professor Wills for his encouragement of us to apply our technical backgrounds to our shared love for basketball. We would also like to thank the staff at basketball-reference.com, as their extensive database of college and NBA players made this project possible. We would finally like to thank Jimmy Johnson, Kevin Pelton, Dr. Aaron Barzilai, and the numerous other analysts who’s work informed our own, providing guidance and comparisons. We hope our work will make a meaningful contribution to the growing body of literature involving sports data mining. ii Table of Contents Abstract ........................................................................................................................................... -

Nba Draft Review • Edición 2019 •
Esperando Marzo • NBA DRAFT REVIEW • EDICIÓN 2019 • NBA DRAFT 2019: LOTERÍA Y DRAFT BOARD NBA DRAFT 2019: OBJETIVOS POR FRANQUICIA NBA DRAFT PROFILES 2019 Nickeil Alexander-Walker | R.J. Barrett | Tyus Battle | Darius Bazley | Goga Bitadze | Bol Bol Phil Booth | Brian Bowen II | Ignas Brazdeikis | Oshae Brissett | Barry Brown Jr. | Bryce Brown Jordan Caroline | Brandon Clarke | Nicolas Claxton | Chris Clemons | Jarrett Culver | Mike Daum | Corey Davis Jr. | Luguentz Dort | Sekou Doumbouya | Carsen Edwards | Tacko Fall Bruno Fernando | Daniel Gafford | Darius Garland | Kyle Guy | Rui Hachimura | Ethan Happ Jaxson Hayes | Tyler Herro | Amir Hinton | Jaylen Hoard | Aric Holman | Talen Horton-Tucker De'Andre Hunter | Ty Jerome | Cameron Johnson | Keldon Johnson | Mfiondu Kabengele Louis King | Romeo Langford | Jalen Lecque | Nassir Little | Fletcher Magee | Terance Mann Caleb Martin | C.J. Massinburg | Luke Maye | Jalen McDaniels | Ja Morant | Juwan Morgan Jordan Murphy | Jaylen Nowell | Chuma Okeke | K.Z. Okpala | Miye Oni | Eric Paschall Shamorie Ponds | Jordan Poole | Jontay Porter | Kevin Porter Jr. | Cam Reddish | Naz Reid Kerwin Roach | Isaiah Roby | Luka Samanic | Admiral Schofield | Marial Shayok | Matisse Thybulle | Lagerald Vick | Dean Wade | P.J. Washington | Tremont Waters | Quinndary Weatherspoon | Coby White | Kris Wilkes | Grant Williams | Kenny Williams | Zion Williamson Dylan Windler | Kenny Wooten NBA DRAFT 2019 LOTERÍA Y DRAFT BOARD La lotería del draft es uno de los eventos más interesantes de este NBA Draft. Un sistema que se lleva implantando oficialmente desde 1985 -con diversas modificaciones desde entonces- y que establece el orden de elección de jugadores del draft para los llamados lottery teams, los 14 equipos que no han logrado su clasificación para los Playoffs de la NBA de la temporada anterior.