DOCSLIB.ORG

The Beta Decay of 79,80,81Zn and Nuclear Structure Around the N=50 Shell Closure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Beta Decay of 79,80,81Zn and Nuclear Structure Around the N=50 Shell Closure University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 12-2011 The Beta Decay of 79,80,81Zn and Nuclear Structure around the N=50 Shell Closure Stephen William Padgett [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Part of the Nuclear Commons Recommended Citation Padgett, Stephen William, "The Beta Decay of 79,80,81Zn and Nuclear Structure around the N=50 Shell Closure. " PhD diss., University of Tennessee, 2011. https://trace.tennessee.edu/utk_graddiss/1212 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Stephen William Padgett entitled "The Beta Decay of 79,80,81Zn and Nuclear Structure around the N=50 Shell Closure." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Physics. Robert Grzywacz, Major Professor We have read this dissertation and recommend its acceptance: Witek Nazarewicz, Carrol Bingham, Jason Hayward Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) The Beta Decay of 79;80;81Zn and Nuclear Structure around the N=50 Shell Closure A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Stephen William Padgett December 2011 Dedication To my father, who has always given me support in my academic pursuits and has never doubted my abilities. Abstract This dissertation reports on new information in the β−[beta minus] decay of the neutron- rich nucleus 81Zn, which populates states in its daughter nucleus 81Ga. This includes new γ[gamma]-ray transitions in the daughter nucleus, 81Ga, as well as a β[beta]-delayed neutron branching ratio. This isotope was produced at the Holifield Radioactive Ion Beam Facility of Oak Ridge National Laboratory through the Isotope Separation Online technique. They are fission fragments from proton-induced fission on a uranium carbide target. These fission fragments are ionized and both mass and isotopically separated before arriving at the Low Energy Radioactive Ion Beam Spectroscopy Station (LeRIBSS). The γ[gamma]-ray and β[beta] electron emissions from the decays are measured and analyzed in this work. A new β[beta]-delayed neutron branching ratio is reported for this decay, which is in agree- ment with recent theoretical values. The core excited states in the daughter nucleus, 81Ga, populated through allowed Gamow-Teller decays are analyzed. A trend in core excited states with other N=50 isotones indicates an increasing gap between a deeply bound neu- tron hole and the valence neutron above the N=50 gap upon moving towards doubly magic 78Ni. This dissertation also reports on additions to the decay schemes of 79Zn and 80Zn decays. Their decay level schemes have been expanded upon and an improved picture of the total allowed Gamow-Teller decay strength is known from 79Zn to 81Zn. This work presents an improved, albeit still incomplete, picture of the energy of states populated through Gamow-Teller decays from below to above the N=50 shell gap in zinc isotopes. iii Contents 1 Introduction 1 2 Theoretical Background 3 2.1 Shell model of the atomic nucleus . 3 2.1.1 Central potential . 3 2.1.2 Spin-orbit splitting . 5 2.2 Experimental evidence of shell gaps and magic numbers . 8 2.3 Microscopic description of β decay . 8 2.4 Fermi and Gamow-Teller operators . 12 2.5 Decay lifetimes, energetics, and selection rules . 14 2.6 β decay branching ratios . 18 3 Experimental studies of the neutron-rich isotopes of Zn 20 3.1 Introduction . 20 3.2 Experimental details . 21 3.2.1 ISOL technique at the HRIBF . 21 3.2.2 Charge exchange cell . 22 3.2.3 High resolution isobar magnets . 23 3.2.4 Charge state contaminants . 26 3.3 LeRIBSS . 26 3.3.1 Electrostatic deflector and tape system . 27 3.3.2 Detector system . 29 3.3.3 HPGe energy and efficiency calibrations . 31 3.3.4 Plastic scintillators for β decay detection . 35 3.3.5 Microchannel plate detector . 36 3.3.6 Digital data acquisition . 39 4 Experimental Analysis and Results: 81Zn 45 4.1 Data reduction methods . 45 4.2 Construction of the decay level scheme . 47 4.2.1 Intensity balance . 49 4.2.2 The β − γ − γ coincidences . 49 4.2.3 Half-life measurements . 50 4.2.4 β efficiency calculation . 51 iv 4.2.5 Determination of isobaric contamination . 54 4.3 Level scheme for 81Zn decay . 57 4.3.1 The 802 keV transition and M1 hindrance . 58 4.3.2 Coincidences and crossover transitions . 59 4.3.3 β decay branching ratios . 60 4.3.4 Neutron emission branching ratio . 60 4.3.5 Neutron branching ratio: Compare to theoretical predictions and prior values from literature . 64 4.4 Pandemonium effect and ground state branching ratio . 65 4.4.1 Pandemonium: Basic information . 66 4.4.2 Estimation of missing β decay intensity . 67 5 Interpretations and Calculations for 81Zn Decay 71 5.1 Theoretical shell model calculations . 71 5.2 N=51 systematics . 72 5.2.1 Previous experiments on N=51 systematics . 73 5.2.2 81Zn ground state Jπ .............................. 73 5.2.3 Calculations on N=51 isotones . 75 5.3 Core excitations of 78Ni ................................ 79 5.3.1 Core excited states in N=50 isotones . 79 5.3.2 Possible N=50 and N=40 shell gap changes . 81 5.4 Predictions for 79Ni and 79Cu............................. 82 6 The Decay Scheme of 79Zn 85 6.1 Verification of original 79Zn decay scheme . 85 6.2 Placement of new transitions in the 79Zn decay scheme . 87 6.3 79Zn decay scheme discussion . 90 6.4 Isomers in N=49 nuclei . 92 79 6.5 Measured Sβ and calculated B(GT) values in Zn decay . 94 6.6 79Zn decay conclusions . 97 7 The Decay Scheme of 80Zn 98 7.1 Verification of original 80Zn decay scheme . 98 7.2 Placement of new transitions in the 80Zn decay scheme . 100 7.3 Isomeric state in 80Ga . 101 v 7.4 Discussion on ground state branching ratio . 103 80 7.5 Measured Sβ and calculated B(GT) values in Zn decay . 103 7.6 80Zn decay conclusions . 105 8 Conclusions and Summary 106 9 My Contributions 109 10 VITA 115 vi List of Figures 1 Woods-Saxon potential . 4 2 Shell model of the atomic nucleus . 7 3 First excited 2+ states and shell gaps . 9 4 Feynman diagram of β− decay . 10 5 Log ft values for allowed decays . 16 6 Log ft values for forbidden decays . 16 7 Nuclear structure and energetics determination of β decay intensity distribution . 19 8 Vertical focusing in the high resolution isobar magnet . 24 9 Horizontal focusing in the high resolution isobar magnet . 25 10 LeRIBSS experimental setup . 27 11 MTC cycles . 28 12 The CARDS with plastic scintillators . 30 13 Efficiency vs. energy for the germanium detectors . 34 14 Microchannel plate detector . 37 15 Pixie16 board layout . 40 16 Trapezoidal filter . 41 17 Trigger threshold vs. data acquisition efficiency . 42 18 Integration time vs. trigger threshold . 42 19 Integration time and source detection example . 43 20 The two dimensional spectrum of energy vs. time with grow-in of activity . 46 21 The γ-ray spectrum for 81Zn decay . 48 22 The intensity balance . 50 23 Efficiency of β electron detection in the scintillators . 53 24 Fit to zinc activity grow-in for isobaric purity determination . 55 25 Fit to gallium activity grow-in for isobaric purity determination . 56 26 The β − γ − γ coincidences in 81Zn decay . 59 27 The level scheme for the decay of 81Zn to 81Ga . 61 28 Neutron branching ratio determination for 81Zn decay . 62 29 Predictions for zinc neutron branching ratios . 65 30 Pandemonium . 66 31 N=51 systematics, including shell model calculations . 77 32 Auxiliary N=51 isotone calculations . 78 33 First forbidden vs. Gamow-Teller decays in the 78Ni region . 80 vii 34 Core excited states in N=50 isotones . 81 35 Predictions for 79Ni and 79Cu............................. 84 36 The γ-ray spectrum for 79Zn decay . 86 37 The level scheme for the decay of 79Zn to 79Ga . 89 38 Systematics for gallium isotopes . 93 79 39 The experimental Sβ values in Ga . 95 40 The theoretical B(GT) values in 79Ga . 96 41 The γ-ray.
Load more

Recommended publications
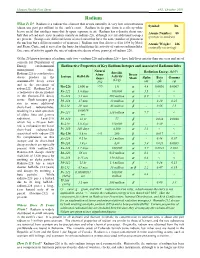
  • Radium What Is It? Radium Is a Radioactive Element That Occurs Naturally in Very Low Concentrations Symbol: Ra (About One Part Per Trillion) in the Earth’S Crust
    Human Health Fact Sheet ANL, October 2001 Radium What Is It? Radium is a radioactive element that occurs naturally in very low concentrations Symbol: Ra (about one part per trillion) in the earth’s crust. Radium in its pure form is a silvery-white heavy metal that oxidizes immediately upon exposure to air. Radium has a density about one- Atomic Number: 88 half that of lead and exists in nature mainly as radium-226, although several additional isotopes (protons in nucleus) are present. (Isotopes are different forms of an element that have the same number of protons in the nucleus but a different number of neutrons.) Radium was first discovered in 1898 by Marie Atomic Weight: 226 and Pierre Curie, and it served as the basis for identifying the activity of various radionuclides. (naturally occurring) One curie of activity equals the rate of radioactive decay of one gram (g) of radium-226. Of the 25 known isotopes of radium, only two – radium-226 and radium-228 – have half-lives greater than one year and are of concern for Department of Energy environmental Radioactive Properties of Key Radium Isotopes and Associated Radionuclides management sites. Natural Specific Radiation Energy (MeV) Radium-226 is a radioactive Abun- Decay Isotope Half-Life Activity decay product in the dance Mode Alpha Beta Gamma (Ci/g) uranium-238 decay series (%) (α) (β) (γ) and is the precursor of Ra-226 1,600 yr >99 1.0 α 4.8 0.0036 0.0067 radon-222. Radium-228 is a radioactive decay product Rn-222 3.8 days 160,000 α 5.5 < < in the thorium-232 decay Po-218 3.1 min 290 million α 6.0 < < series.
    [Show full text]
  • Nuclear Structure of Yrast Bands of 180Hf, 182W, and 184Os Nuclei by Means of Interacting Boson Model-1
    ESEARCH ARTICLE R ScienceAsia 42 (2016): 22–27 doi: 10.2306/scienceasia1513-1874.2016.42.022 Nuclear structure of yrast bands of 180Hf, 182W, and 184Os nuclei by means of interacting boson model-1 a, b b a,c I. Hossain ∗, Huda H. Kassim , Fadhil I. Sharrad , A.S. Ahmed a Department of Physics, Rabigh College of Science and Arts, King Abdulaziz University, Rabigh 21911, Saudi Arabia b Department of Physics, College of Science, University of Kerbala, 56001 Karbala, Iraq c Department of Radiotherapy, South Egypt Cancer Institute, Asyut University, Egypt ∗Corresponding author, e-mail: [email protected] Received 30 Jul 2015 Accepted 30 Nov 2015 ABSTRACT: In this paper, an interacting boson model (IBM-1) has been used to calculate the low-lying positive parity yrast bands in Hf, W, and Os nuclei for N = 108 neutrons. The systematic yrast level, electric reduced transition probabilities B(E2) , deformation, and quadrupole moments of those nuclei are calculated and compared with the # + + available experimental values. The ratio of the excitation energies of first 4 and first 2 excited states, R4/2, is also studied for these nuclei. Furthermore, as a measure to quantify the evolution, we have studied systematically the yrast level R = (E2 : L+ (L 2)+)=(E2 : 2+ 0+) of some low-lying quadrupole collective states in comparison to the available experimental! data.− The associated! quadrupole moments and deformation parameters have also been calculated. Moreover, we have studied the systematic B(E2) values, intrinsic quadrupole moments, and deformation parameters in those nuclei. The moment of inertia as a function of the square of the rotational energy for even atomic numbers Z = 72, 74, 76 and N = 108 nuclei indicates the nature of the back-bending properties.
    [Show full text]
  • Neutrinoless Double Beta Decay
    REPORT TO THE NUCLEAR SCIENCE ADVISORY COMMITTEE Neutrinoless Double Beta Decay NOVEMBER 18, 2015 NLDBD Report November 18, 2015 EXECUTIVE SUMMARY In March 2015, DOE and NSF charged NSAC Subcommittee on neutrinoless double beta decay (NLDBD) to provide additional guidance related to the development of next generation experimentation for this field. The new charge (Appendix A) requests a status report on the existing efforts in this subfield, along with an assessment of the necessary R&D required for each candidate technology before a future downselect. The Subcommittee membership was augmented to replace several members who were not able to continue in this phase (the present Subcommittee membership is attached as Appendix B). The Subcommittee solicited additional written input from the present worldwide collaborative efforts on double beta decay projects in order to collect the information necessary to address the new charge. An open meeting was held where these collaborations were invited to present material related to their current projects, conceptual designs for next generation experiments, and the critical R&D required before a potential down-select. We also heard presentations related to nuclear theory and the impact of future cosmological data on the subject of NLDBD. The Subcommittee presented its principal findings and comments in response to the March 2015 charge at the NSAC meeting in October 2015. The March 2015 charge requested the Subcommittee to: Assess the status of ongoing R&D for NLDBD candidate technology demonstrations for a possible future ton-scale NLDBD experiment. For each candidate technology demonstration, identify the major remaining R&D tasks needed ONLY to demonstrate downselect criteria, including the sensitivity goals, outlined in the NSAC report of May 2014.
    [Show full text]
  • RIB Production by Photofission in the Framework of the ALTO Project
    Available online at www.sciencedirect.com NIM B Beam Interactions with Materials & Atoms Nuclear Instruments and Methods in Physics Research B 266 (2008) 4092–4096 www.elsevier.com/locate/nimb RIB production by photofission in the framework of the ALTO project: First experimental measurements and Monte-Carlo simulations M. Cheikh Mhamed *, S. Essabaa, C. Lau, M. Lebois, B. Roussie`re, M. Ducourtieux, S. Franchoo, D. Guillemaud Mueller, F. Ibrahim, J.F. LeDu, J. Lesrel, A.C. Mueller, M. Raynaud, A. Said, D. Verney, S. Wurth Institut de Physique Nucle´aire, IN2P3-CNRS/Universite´ Paris-Sud, F-91406 Orsay Cedex, France Available online 11 June 2008 Abstract The ALTO facility (Acce´le´rateur Line´aire aupre`s du Tandem d’Orsay) has been built and is now under commissioning. The facility is intended for the production of low energy neutron-rich ion-beams by ISOL technique. This will open new perspectives in the study of nuclei very far from the valley of stability. Neutron-rich nuclei are produced by photofission in a thick uranium carbide target (UCx) using a 10 lA, 50 MeV electron beam. The target is the same as that already had been used on the previous deuteron based fission ISOL setup (PARRNE [F. Clapier et al., Phys. Rev. ST-AB (1998) 013501.]). The intended nominal fission rate is about 1011 fissions/s. We have studied the adequacy of a thick carbide uranium target to produce neutron-rich nuclei by photofission by means of Monte-Carlo simulations. We present the production rates in the target and after extraction and mass separation steps.
    [Show full text]
  • The Use of Cosmic-Rays in Detecting Illicit Nuclear Materials
    The use of Cosmic-Rays in Detecting Illicit Nuclear Materials Timothy Benjamin Blackwell Department of Physics and Astronomy University of Sheffield This dissertation is submitted for the degree of Doctor of Philosophy 05/05/2015 Declaration I hereby declare that except where specific reference is made to the work of others, the contents of this dissertation are original and have not been submitted in whole or in part for consideration for any other degree or qualification in this, or any other Univer- sity. This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration, except where specifically indicated in the text. Timothy Benjamin Blackwell 05/05/2015 Acknowledgements This thesis could not have been completed without the tremendous support of many people. Firstly I would like to express special appreciation and thanks to my academic supervisor, Dr Vitaly A. Kudryavtsev for his expertise, understanding and encourage- ment. I have enjoyed our many discussions concerning my research topic throughout the PhD journey. I would also like to thank my viva examiners, Professor Lee Thomp- son and Dr Chris Steer, for the time you have taken out of your schedules, so that I may take this next step in my career. Thanks must also be given to Professor Francis Liven, Professor Neil Hyatt and the rest of the Nuclear FiRST DTC team, for the initial oppor- tunity to pursue postgraduate research. Appreciation is also given to the University of Sheffield, the HEP group and EPRSC for providing me with the facilities and funding, during this work.
    [Show full text]
  • Chapter 3 the Fundamentals of Nuclear Physics Outline Natural
    Outline Chapter 3 The Fundamentals of Nuclear • Terms: activity, half life, average life • Nuclear disintegration schemes Physics • Parent-daughter relationships Radiation Dosimetry I • Activation of isotopes Text: H.E Johns and J.R. Cunningham, The physics of radiology, 4th ed. http://www.utoledo.edu/med/depts/radther Natural radioactivity Activity • Activity – number of disintegrations per unit time; • Particles inside a nucleus are in constant motion; directly proportional to the number of atoms can escape if acquire enough energy present • Most lighter atoms with Z<82 (lead) have at least N Average one stable isotope t / ta A N N0e lifetime • All atoms with Z > 82 are radioactive and t disintegrate until a stable isotope is formed ta= 1.44 th • Artificial radioactivity: nucleus can be made A N e0.693t / th A 2t / th unstable upon bombardment with neutrons, high 0 0 Half-life energy protons, etc. • Units: Bq = 1/s, Ci=3.7x 1010 Bq Activity Activity Emitted radiation 1 Example 1 Example 1A • A prostate implant has a half-life of 17 days. • A prostate implant has a half-life of 17 days. If the What percent of the dose is delivered in the first initial dose rate is 10cGy/h, what is the total dose day? N N delivered? t /th t 2 or e Dtotal D0tavg N0 N0 A. 0.5 A. 9 0.693t 0.693t B. 2 t /th 1/17 t 2 2 0.96 B. 29 D D e th dt D h e th C. 4 total 0 0 0.693 0.693t /th 0.6931/17 C.
    [Show full text]
  • Radioactive Decay
    North Berwick High School Department of Physics Higher Physics Unit 2 Particles and Waves Section 3 Fission and Fusion Section 3 Fission and Fusion Note Making Make a dictionary with the meanings of any new words. Einstein and nuclear energy 1. Write down Einstein’s famous equation along with units. 2. Explain the importance of this equation and its relevance to nuclear power. A basic model of the atom 1. Copy the components of the atom diagram and state the meanings of A and Z. 2. Copy the table on page 5 and state the difference between elements and isotopes. Radioactive decay 1. Explain what is meant by radioactive decay and copy the summary table for the three types of nuclear radiation. 2. Describe an alpha particle, including the reason for its short range and copy the panel showing Plutonium decay. 3. Describe a beta particle, including its range and copy the panel showing Tritium decay. 4. Describe a gamma ray, including its range. Fission: spontaneous decay and nuclear bombardment 1. Describe the differences between the two methods of decay and copy the equation on page 10. Nuclear fission and E = mc2 1. Explain what is meant by the terms ‘mass difference’ and ‘chain reaction’. 2. Copy the example showing the energy released during a fission reaction. 3. Briefly describe controlled fission in a nuclear reactor. Nuclear fusion: energy of the future? 1. Explain why nuclear fusion might be a preferred source of energy in the future. 2. Describe some of the difficulties associated with maintaining a controlled fusion reaction.
    [Show full text]
  • Two-Proton Radioactivity 2
    Two-proton radioactivity Bertram Blank ‡ and Marek P loszajczak † ‡ Centre d’Etudes Nucl´eaires de Bordeaux-Gradignan - Universit´eBordeaux I - CNRS/IN2P3, Chemin du Solarium, B.P. 120, 33175 Gradignan Cedex, France † Grand Acc´el´erateur National d’Ions Lourds (GANIL), CEA/DSM-CNRS/IN2P3, BP 55027, 14076 Caen Cedex 05, France Abstract. In the first part of this review, experimental results which lead to the discovery of two-proton radioactivity are examined. Beyond two-proton emission from nuclear ground states, we also discuss experimental studies of two-proton emission from excited states populated either by nuclear β decay or by inelastic reactions. In the second part, we review the modern theory of two-proton radioactivity. An outlook to future experimental studies and theoretical developments will conclude this review. PACS numbers: 23.50.+z, 21.10.Tg, 21.60.-n, 24.10.-i Submitted to: Rep. Prog. Phys. Version: 17 December 2013 arXiv:0709.3797v2 [nucl-ex] 23 Apr 2008 Two-proton radioactivity 2 1. Introduction Atomic nuclei are made of two distinct particles, the protons and the neutrons. These nucleons constitute more than 99.95% of the mass of an atom. In order to form a stable atomic nucleus, a subtle equilibrium between the number of protons and neutrons has to be respected. This condition is fulfilled for 259 different combinations of protons and neutrons. These nuclei can be found on Earth. In addition, 26 nuclei form a quasi stable configuration, i.e. they decay with a half-life comparable or longer than the age of the Earth and are therefore still present on Earth.
    [Show full text]
  • Heavy Element Nucleosynthesis
    Heavy Element Nucleosynthesis A summary of the nucleosynthesis of light elements is as follows 4He Hydrogen burning 3He Incomplete PP chain (H burning) 2H, Li, Be, B Non-thermal processes (spallation) 14N, 13C, 15N, 17O CNO processing 12C, 16O Helium burning 18O, 22Ne α captures on 14N (He burning) 20Ne, Na, Mg, Al, 28Si Partly from carbon burning Mg, Al, Si, P, S Partly from oxygen burning Ar, Ca, Ti, Cr, Fe, Ni Partly from silicon burning Isotopes heavier than iron (as well as some intermediate weight iso- topes) are made through neutron captures. Recall that the prob- ability for a non-resonant reaction contained two components: an exponential reflective of the quantum tunneling needed to overcome electrostatic repulsion, and an inverse energy dependence arising from the de Broglie wavelength of the particles. For neutron cap- tures, there is no electrostatic repulsion, and, in complex nuclei, virtually all particle encounters involve resonances. As a result, neutron capture cross-sections are large, and are very nearly inde- pendent of energy. To appreciate how heavy elements can be built up, we must first consider the lifetime of an isotope against neutron capture. If the cross-section for neutron capture is independent of energy, then the lifetime of the species will be ( )1=2 1 1 1 µn τn = ≈ = Nnhσvi NnhσivT Nnhσi 2kT For a typical neutron cross-section of hσi ∼ 10−25 cm2 and a tem- 8 9 perature of 5 × 10 K, τn ∼ 10 =Nn years. Next consider the stability of a neutron rich isotope. If the ratio of of neutrons to protons in an atomic nucleus becomes too large, the nucleus becomes unstable to beta-decay, and a neutron is changed into a proton via − (Z; A+1) −! (Z+1;A+1) + e +ν ¯e (27:1) The timescale for this decay is typically on the order of hours, or ∼ 10−3 years (with a factor of ∼ 103 scatter).
    [Show full text]
  • Some Aspects of High(Ish) - Spin Nuclear Structure
    Some Aspects of High(ish) - Spin Nuclear Structure Paddy Regan Department of Physics University of Surrey Guildford, UK [email protected] Outline of Lectures • 1) Overview of nuclear structure ‘limits’ – Some experimental observables, evidence for shell structure – Independent particle (shell) model – Single particle excitations and 2 particle interactions. • 2) Low Energy Collective Modes and EM Decays in Nuclei. – Low-energy Quadrupole Vibrations in Nuclei – Rotations in even-even nuclei – Vibrator-rotor transitions, E-GOS curves • 3) EM transition rates..what they mean and overview of how you measure them – Deformed Shell Model: the Nilsson Model, K-isomers – Definitions of B(ML) etc. ; Weisskopf estimates etc. – Transition quadrupole moments (Qo) – Electronic coincidences; Doppler Shift methods. – Yrast trap isomers – Magnetic moments and g-factors Some nuclear observables? 1) Masses and energy differences 2) Energy levels 3) Level spins and parities 4) EM transition rates between states 5) Magnetic properties (g-factors) 6) Electric quadrupole moments? Essence of nuclear structure physics …….. How do these change as functions of N, Z, I, Ex ? Evidence for Nuclear Shell Structure? • Increased numbers of stable isotones and isotopes at certain N,Z values. • Discontinuities in Sn, Sp around certain N,Z values (linked to neutron capture cross-section reduction). • Excitation energy systematics with N,Z. More number of stable isotones at N=20, 28, 50 and 82 compared to neighbours… A-1 A 2 Sn = [ M ( XN-1) – M( XN) + mn) c = neutron
    [Show full text]
  • Microscopic Insight in the Study of Yrast Bands in Selenium Isotopes
    PRAMANA °c Indian Academy of Sciences Vol. 70, No. 5 | journal of May 2008 physics pp. 817{833 Microscopic insight in the study of yrast bands in selenium isotopes PARVAIZ AHMAD DAR, SONIA VERMA, RANI DEVI¤ and S K KHOSA Department of Physics and Electronics, University of Jammu, Jammu 180 006, India ¤Corresponding author. E-mail: rani [email protected] MS received 30 March 2007; revised 19 October 2007; accepted 1 January 2008 Abstract. The yrast bands of even{even selenium isotopes with A = 68{78 are studied in the framework of projected shell model, by employing quadrupole plus monopole and quadrupole pairing force in the Hamiltonian. The oblate and prolate structures of the bands have been investigated. The yrast energies, backbending plots and reduced E2 transition probabilities and g-factors are calculated and compared with the experimental data. The calculated results are in reasonably good agreement with the experiments. Keywords. Selenium isotopes; projected shell model; yrast bands; B(E2) transition probability; g-factors. PACS Nos 21.60.Cs; 21.10.Ky; 21.10.Re; 27.60.+e 1. Introduction The study of selenium isotopes with A = 68{78 has been at the centre stage of nuclear physics for quite sometime in the past [1{41]. Substantial e®ort on the ex- perimental side has been put to investigate the nuclear structure determining prop- erties of these isotopes [1{31]. Presently, experimental data are available on energy spectra, B(E2) transition probabilities, nuclear magnetic g-factors and quadrupole deformation parameters for these isotopes. For example, in 68Se an oblate de- formed ground state band has been observed up to I¼ = 10+ and was found to coexist with a prolate deformed excited band.
    [Show full text]
  • Study of Shape Evolution in the Neutron-Rich Osmium Isotopes with the Advanced Gamma-Tracking Array AGATA
    Universit`adegli Studi di Padova Dipartimento di Fisica e Astronomia \Galileo Galilei" SCUOLA DI DOTTORATO DI RICERCA IN : Fisica CICLO XXVII Study of shape evolution in the neutron-rich osmium isotopes with the advanced gamma-tracking array AGATA Direttore della Scuola : Ch.mo Prof. Andrea Vitturi Supervisori : Dott. Daniele Mengoni Ch.mo Prof. Santo Lunardi Dott. Jos´eJavier Valiente Dob´on Dottorando : Philipp Rudolf John Manchmal muss man eben Leergut zahlen. { Hannes Holzmann This work is licensed under the Creative Commons Attribution-NonCommercial- NoDerivatives 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/ by-nc-nd/4.0/. Abstract This thesis describes the major results of a γ-ray spectroscopy experiment aiming at the investigation of the shape evolution in the neutron-rich even-even osmium isotopes. The first in-beam γ-ray spectroscopy measurement of 196Os has been performed and the results are compared to state-of-the-art beyond mean-field calculations, that have revealed its pre- sumably γ-soft character. Finite many-body systems, such as molecules, many man-made nano materials and atomic nuclei can be understood as a drop of viscous liquids confined by an elastic membrane, where its equilibrium shape (ground state) has a unique feature: the existence of deformed (non-spherical) shapes. Non-spherical shapes represent spontaneous symmetry breaking. However, the shape of the nucleus is not a direct observable. By comparing its low-lying excited states to predictions of nuclear models, the shape of the nucleus can anyway be deduced, as it will be shown in this work.
    [Show full text]