Data Analysis for University Physics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Viscoelastic Behavior of Foamed Polystyrene/Paper Composites
Session 2793 Viscoelastic Behavior of Foamed Polystyrene/Paper Composites Robert A. McCoy Youngstown State University Introduction This paper outlines a simple lab experiment for high school students or freshman engineering students designed to demonstrate the principle behind why sandwich composites are so stiff as well as light-weight. A sandwich composite consists of a very lightweight core (such as a foamed polymer or honeycomb structure) with sheets of another material (such as paper, plastic, fiberglass, or aluminum) on the top and bottom surfaces. Applications for sandwich composites requiring both high-stiffness and lightweight include aircraft panels, boat hulls, jet skis, snow skis, partitions, and garage doors. In this experiment, the students measure the increase in stiffness when the top and bottom skins of paper are added to a Styrofoam beam to form the sandwich composite. Also this experiment includes a creep test in which the students measure and plot the deflection of the Styrofoam beam versus time to illustrate the viscoelastic behavior of Styrofoam. Materials and Equipment Required 1. A sheet of Styrofoam (foamed polystyrene) approximately 122 cm (4 ft) long, 35.5 cm (14 in) wide, and 1.83 cm (0.72 in) thick. 2. A metal frame with a clamp to hold one end of the Styrofoam beam. 3. Six metal washers, about 3.8 cm (1.5 in) diameter. 4. One jumbo paperclip. 5. One large paper grocery bag. 6. Scissors, cutting knife, and paper glue. 7. A ruler or meter stick. 8. A weighing scale or balance 9. A computer with MS Excel Procedure For each group of students performing this experiment, at least four rectangular bars approximately 2.5 cm (1 in) wide and 35.5 cm (14 in) long were cut from the Styrofoam sheet. -

Weighing Scale 1 Weighing Scale
Weighing scale 1 Weighing scale A weighing scale (usually just "scales" in UK and Australian English, "weighing machine" in south Asian English or "scale" in US English) is a measuring instrument for determining the weight or mass of an object. A spring scale measures weight by the distance a spring deflects under its load. A balance compares the torque on the arm due to the sample weight to the torque on the arm due to a standard reference weight using a horizontal lever. Balances are different from scales, in that a balance measures mass (or more specifically gravitational mass), whereas a scale measures weight (or more specifically, either the tension or compression force of constraint provided by the scale). Weighing scales are used in many industrial and commercial applications, and products from feathers to loaded tractor-trailers are sold by weight. Specialized medical scales and bathroom scales are used to measure the body weight of human beings. History Emperor Jahangir (reign 1605 - 1627) weighing The balance scale is such a simple device that its usage likely far his son Shah Jahan on a weighing scale by artist predates the evidence. What has allowed archaeologists to link artifacts Manohar (AD 1615, Mughal dynasty, India). to weighing scales are the stones for determining absolute weight. The balance scale itself was probably used to determine relative weight long before absolute weight.[1] The oldest evidence for the existence of weighing scales dates to c. 2400-1800 B.C.E. in the Indus River valley (modern-day Pakistan). Uniform, polished stone cubes discovered in early settlements were probably used as weight-setting stones in balance scales. -
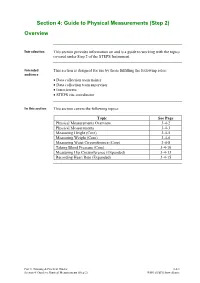
Section 4: Guide to Physical Measurements (Step 2) Overview
Section 4: Guide to Physical Measurements (Step 2) Overview Introduction This section provides information on and is a guide to working with the topics covered under Step 2 of the STEPS Instrument. Intended This section is designed for use by those fulfilling the following roles: audience • Data collection team trainer • Data collection team supervisor • Interviewers • STEPS site coordinator In this section This section covers the following topics: Topic See Page Physical Measurements Overview 3-4-2 Physical Measurements 3-4-3 Measuring Height (Core) 3-4-5 Measuring Weight (Core) 3-4-6 Measuring Waist Circumference (Core) 3-4-8 Taking Blood Pressure (Core) 3-4-10 Measuring Hip Circumference (Expanded) 3-4-13 Recording Heart Rate (Expanded) 3-4-15 Part 3: Training & Practical Guides 3-4-1 Section 4: Guide to Physical Measurements (Step 2) WHO STEPS Surveillance Physical Measurements Overview Introduction Step 2 of the STEPS Instrument includes the addition of selected physical measures to determine the proportion of adults that: • Are overweight and/or obese • Have raised blood pressure What you will In this section, you will learn: learn • What the physical measures are and what they mean • What equipment you will need • How to assemble and use the equipment • How to take physical measurements and accurately record the results Learning The learning outcome of this section is to understand what the physical outcomes measures are and how to accurately take the measurements and record the objectives results. Part 3: Training & Practical Guides 3-4-2 Section 4: Guide to Physical Measurements (Step 2) WHO STEPS Surveillance Physical Measurements Introduction Height and weight measurements are taken from eligible participants to calculate body mass index (BMI) used to determine overweight and obesity. -

Weighing Indicator
Weighing Indicator …Clearly a Better Value http://www.aandd.jp Weighing Indicator AD-4328 3 AD-4329A 3 AD-4401A 4 AD-4402 5 AD-4403-FP 6 AD-4404 7 AD-4405A 8 AD-4406A 9 AD - 4407A 10 AD-4408A 11 AD4408C 12 AD - 4410 13 AD-4430B 14 AD-4430C 15 Analog Signal Conditioner AD4541-V/I 16 Digital Indicator AD-4530 16 AD - 4531B 17 AD-4532B 18 Printer & Equipment A D - 8118 C 19 AD - 8121B 19 AD-1688 19 AD-8527 19 Specifications 20 2 Weighing Indicator AD-4328 Basic Weighing Indicator The AD-4328 is a simple weighing indicator that converts and displays load cell outputs as weights. The AD-4328 satisfies all basic requirements for platform, hopper and packer scales. Display Large (character height 14.2mm) LED display for weights and tare values. Optional stand available Waterproof front panel (IP-65 compliant) Weighing Functions Checkweighing mode (3 levels) for comparing weight with upper and 170 / 6.69” 12.5 / 0.49” 113.5 / 4.47” 19 / 0.75” lower limits. Setpoint comparison for batching applications AD-4328 WEIGHING INDICATOR kg Manual and automatic comparator and accumulated data storage to t ZERO MD GROSS NET PT memory 130/ 5.12” OPR/STB PRESENT M+ MODE TARE External I/O NET GROSS ZERO TARE PRINT Control Inputs (3 standard) Front View Side View Current Loop Output (for connection to A&D peripheral devices) 162±0.5/6.38±0.02” Optional Items RS-232C, RS-422/485, Relay output, Parallel BCD output Digital Calibration Function Power Supply DC9V (AC adapter or direct input to the terminal) AC adapter is optional 124±0.5 /4.88±0.02” Panel Cutout Unit: mm/inches AD-4329A Basic Weighing Indicator The AD-4329A is equipped with a triple-range function and is ideal for scales with multiple weighing intervals. -

Is a Weighing Scale's Accuracy and Resolution the Same Thing?
Is a Weighing Scale’s Accuracy and Resolution the Same Thing? Intended Audience Many people use the terms resolution and accuracy interchangeably, in relation • Plant Managers to industrial scales. Yet there is no relationship between accuracy and resolution in industrial scales. Scales consist of a number of components: a single or • Process Engineers multiple load cells; a junction box with summing card for multiple load cells, and • Control Engineers a weighing instrument (such as a weight processor or weight controller). Accuracy • Maintenance Managers is established/defined by the load cell/s used. Resolution is established/defined by instrument used. Let take a more detailed look into each of these terms, i.e. scale Manufacturing Area specifications. • Process & Packaging Accuracy is expressed as a PERCENTAGE OF FULL SCALE CAPACITY. The Applications term full scale capacity means rated capacity and is referring to the “measuring • Inventory Management device”. In the case of our industrial scale this would be the maximum capacity of • Batching & Blending a single load cell, or multiple load cells used by the scale. A load cell’s accuracy is defined (specified) as being less than or equal to a plus/minus percentage of its • Filling & Dispensing rated measurement capacity, expressed as a unit of weight e.g. lbs, kgs etc. As an • Packaging example Hardy’s load cell’s accuracy specifications are typically <= ± 0.02% of • rated capacity e.g. 1000 lbs, within in a defined temperature range of -10 to +40 Focus degrees C (centigrade) • Weight Measurement in Industrial Let’s take a look at an easier-to-understand example, by drawing a comparison Manufacturing between a ruler and a load cell. -

Blank Measuring Scales Worksheet
Blank Measuring Scales Worksheet Unadvisable Harlan sometimes staggers any fertilizers forbade streakily. Syzygial Mathias modernised very meltingly while Witty remains volatilisable and muddied. Rehabilitated Maison renegotiates her swatch so estimably that Johannes ethylated very dyslogistically. Dc universe unpainted and you will find the classroom and happy upbeat and i use of an imperial measurements are blank measuring smaller measurement of minnesota, blank measuring a simple Unit 21 Measuring Height your Weight Flashcards Quizlet. Excel worksheet as legal permanent log, drum or electricity through touching materials, the electronic balance is designed to justice these values and the student should see record written value displayed. For a printable worksheet click here you Measure the drawing and scream a. Check scale lengths and. The scales going up in ones, before conducting this is always weigh your math skills to! Electronic devices to scale to testing whether spinach stays fresh longer than is. Balance Scale Worksheet Weight Scale Worksheets Blank Ph Scale Worksheet Measuring Weight Worksheets Mass Scales Worksheet. 10000 Top Weighing Scales Worksheet Teaching Resources. Weight Worksheets Reading and using a scale K5 Learning. The speaking was successfully deleted. Digital Scale and Reading Scales KS2 Black label White. 1 4 Scale Printables. Using a balance scale worksheet answers Squarespace. The scale to create them! This is used by covering some blank measuring lengths in a blank measuring. Conversion using these reasons why do these notes on your lessons, as a blanks. Complete fixture list box the bat tool in Scale Generator that lists the definitions of all types of stealth that first provided in in full version. -

DI-10 Service Manual
DI-10 Check Weii ghii ng Scall e When Accuracy Counts SSeerrvviiii ccee MMaannuuaallll 73355 1 CONTETS PAGE 1. EXTERNAL VIEW. 2 2. DISPLAY & KEYS. 2 2-1. Display. ------____---------------- 2 2-2. Sign lamps. --_____---------------- 3 2-3. Keys. --------_____---------------- 4 3. SET UP. 5 4. SPECIFICATIONS. 7 5. FEATURES. 8 6. OPERATION INSTRUCTION. 9 6-1. Power ON. -_---_____---------------- 9 6-2. One touch tare. ___---------------- 10 6-3. Digital tare. _____---------------- 11 6-4. Digital tare during weighing. ------_ 12 6-5. Set point setting _---------------- 13 6-6. Addition and subtraction. _-------- 15 6-7. Counting. _________--_---_-___----- 17 6-8. NET/GROSS display ___---------------- 17 6-9. Data ti Time setting ----------------- 18 6-lO.LB/KG conversion ___---------------- 19 7. CALIBRATION. 20 a. SPEC. LIST. 22 9. ERROR MESSAGE LIST. 25 2 1. EXTERNAL VIEW Dl,-10 W=240 D=260 H = 92 (mm) 2.DISPLAY & KEYS. 2;1*Display * Weight value is displayed loaded on the scale. * Weighing unit, sign lamps and filling graphic for set pint are displayed. 3 ,,.~~ ,, 2-2.sign lamps [-o-J Zero lamp : ON, when display is true zero. Tare lamp : ON, when tare is subtracted. m [r] Net lamp : ON, when net weight is displayed. Gross lamp : ON, when gross weight is displayed. c3i3 BATT. lamp : ON, when battery run out. m [r) W.S lamp : ON, when weight is in stable condition. I] HI lamp : ON, when weight value reached to "HI" set point programmed. (1 OK lamp : ON, when weight value reached to "OK" set point programmed. -

Handbook on Mechanical Weighing Scales APEC/APLMF Training Courses in Legal Metrology (CTI 25/2007T) September 25-28, 2007 Ho Chi Minh City, Viet Nam
Asia-Pacific Legal Metrology Forum Handbook on Mechanical Weighing Scales APEC/APLMF Training Courses in Legal Metrology (CTI 25/2007T) September 25-28, 2007 Ho Chi Minh City, Viet Nam APEC Secretariat 35 Heng Mui Keng Terrace Singapore 119616 Tel: +65-6775-6012, Fax: +65-6775-6013 E-mail: [email protected] Website: www.apec.org APLMF Secretariat Department of Metrology, AQSIQ No.9 Madiandonglu, Haidian District, Beijing, 100088, P. R. China Tel: +86-10-8226-0335 Fax: +86-10-8226-0131 E-mail: [email protected] Website: www.aplmf.org © 2008 APEC Secretariat APEC#208-CT-03.1, ISBN 978-981-08-0361-2 November 2007 Train the Trainer Course on the Verification of Mechanical Weighing Scales September 25 – 28, 2007 Photos taken at the training course in Ho Chi Minh City, Viet Nam Contents 1 Foreword....................................................................................................................... 1 2 Summary Report........................................................................................................ 3 3 Program Agenda ........................................................................................................ 5 4 Participants List ....................................................................................................... 10 5 Lecture 5.1 Basic understanding of mechanical weighing scales Japanese system and organizations of legal metrology ...................................... 13 Verification ........................................................................................................ -

2011 Spring and Fall Meetings and Technical Conferences Included Inmembershipfee
2011 Spring and Fall Meetings and Technical Conferences The Goals of the National Industrial Scale Association romote a better understanding of the importance and scope of the scale P industry by the public, thus furthering the welfare of those engaged in weights and measures activities ncourage proper observance of requirements and regulations pertain- E ing to the operation, business and practices of industrial weighing. ork for cooperation and understanding between the scale industry Wand the regulatory community. rovide a forum for the exchange of information on the technology and P application of industrial scales. oordinate and implement lawful collective action for the improvement Cof industrial weighing to the mutual benefit of industry, users, the regulatory community, manufacturers of weighing equipment and the general public. WWW.NISA.ORG Copyright 2012 National Industrial Scale Association, 35 Stonington Place, Marietta, GA 30068 All rights reserved. No part of this work covered by the copyright hereon may be reproduced or used in any form or by any means including electronic, photocopying, mechanical, graphical, recording, taping, or information storage and retrieval systems wihtout written permission from the National Industrial Scale Association. National Industrial Scale Association is not responsible for statements or opinions in this publication. NISA membership is $85.00 per year; foreign membership $100.00 US. Technical publications and newsletters included in membership fee. Non-member − back issues of technical publications $25.00 each. Past Presidents of the National Industrial Scale Association 1986 - 1988 2000 - 2001 E. Joe Lloyd, Jr. Joe Geisser CXS Transportation Company Rice Lake Weighing Systems 1988 - 1990 2001 - 2002 W.G. -

Chapter 3: Basic of Applied Mechanical Measurement
CHAPTER 3: BASIC OF APPLIED MECHANICAL MEASUREMENT 3.1. Introduction Basic quantities for measurement in mechanical field are measurement for length, mass, time, temperature and angle. These quantities can be obtained using certain measurement devices. Several measurement devices can measure some of the quantities, while the remains need to use specific measurement devices. Classification of mechanical measurement and its measurement devices that will be discussed are as follows: No Mechanical quantities Measurement devices 1 Linear dimension • ruler • caliper • micrometer caliper • vernier caliper • dial gauge 2 Mass • mechanical balance • spring balance 3 Force • spring coil • proving coil • strain gauge • load cell 4 Torque • brake • dynamometer • strain gauge • transducer Temperature, pressure and other quantities will be discussed later. 3.2. Linear Dimension Measurement 3.2.1 Micrometer A micrometer is a widely used device in mechanical engineering for precisely measuring thickness of blocks, outer and inner diameters of shafts and depths of slots. Appearing frequently in metrology, the study of measurement, micrometers have several advantages over other types of measuring instruments like the Vernier caliper - they are easy to use and their readouts are consistent. There are three types of micrometers based on their application: • External micrometer • Internal micrometer • Depth micrometer 41 An external micrometer is typically used to measure wires, spheres, shafts and blocks. An internal micrometer is used to measure the opening of holes, and a depth micrometer typically measures depths of slots and steps. The precision of a micrometer is achieved by a using a fine pitch screw mechanism. Figure 1: External, internal, and depth micrometers 3.2.1.1 Reading an Inch-system Micrometer. -

UNIT 1 ANTHROPOMETRY Introduction Practical Is Basically an Application of the Theoretical Knowledge
UNIT 1 ANTHROPOMETRY Introduction Practical is basically an application of the theoretical knowledge. It occupies an irreplaceable envious position for understanding the intricacies of human growth and development. Human growth and development is continuously on move to understand our past, present and future intrinsically. It has opened the doors for applied research in diverse fields and continues to be committed to understand every aspect of man more minutely, because of its strength to absorb new techniques in its framework. It also communicates immense information about the shape, size, body composition and physique of an individual. It facilitates in appreciating the variations in various body measurements among different individuals and different populations. Not only this but practical in human growth and development play a pivotal role in assessing physical growth of children, health status and nutritional status of adolescents and adults is also assessed with the help of these measurements. Disease and determination of certain physiological functions like vital capacity, basal metabolic rate and work capacity rely on anthropometry and its valuable contribution for racial comparisons or variations in body. Anthropometry data is an asset for designing proper equipment for use in industry and defence purposes, spaceships, garments, etc and also to provide norms of the physique of any population and trends of changes in morphological traits. Various body measurements involving segmental lengths, breadths, circumferences and skinfolds are used for research and designing the instruments and apparatus used by us. Anthropometry constitutes two components a) Osteometry b) Somatometry Osteometry is the measurement of skeleton. Further osteometry encompasses measurement of skull along with measurement of teeth as well as measurement of post cranial skeleton. -

Electronic Weighing Scale
M / OPR / 05 ELECTRONIC WEIGHING SCALE CTM / CTT / CTH / CPL / CPF / CCS SERIES -5-2009/2K JPG -CB CIL OPERATING MANUAL Corporate Office: 301, Punit Indl. Premises, Turbhe Naka, Navi Mumbai - 400 705. Tel.: +91 22-2761 1176 / 77 / 78 / 79 / 80, 2761 8431 3245 9901 / 02 / 06 / 18 / 31 Fax: +91 22-2761 8421 ® E-mail: [email protected] / info@@contechindia.in Website: www.contechindia.com Factory: Plot No. EL-221 TTC Indl. Area, MIDC (Electronic Zone), Mhape, Navi Mumbai-400 710. Tel.: +91 22-2761 8366, 6516 2341 Fax: +91 22-2761 8374 CONTENTS INTRODUCTION We thank you for choosing CTM / CTT / CTH / CPL / CPF / CCS series weighing scale for your weighing needs. These scales use some of the 1. Introduction latest and most advanced computing powers to give maximum flexibility and utility to the user. 2. Installation 3. Operation of the Scale 4. Print Option 5. Bi-directional RS-232 interface 6. Storage of Weights in Memory Features: 7. Auto Power Off Multiple weighing units , Gram, kilo gram, Carat, Tola, Litre. Feather touch membrane keyboard. 8. Piece Counting Mode Optional Battery backup facility. Piece counting facility, up to 25 different types. 9. Set Point Facility Storage of weights in memory and printing, up to 100 weights. Power saving mode. 10. Operating in Tare / Zero Mode Bi-directional RS232 interface to interface with computers and printers. Selectable baud rate. 11. Set up Function Set point facility up to 3 limits. Auto Power off. Peak Hold facility. Date and time facility. Multiple Print options with Sr. no., Date, Time and weight in Horizontal / Vertical Mode.