PME-NA 36 (Vol
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Flächennutzungsplan 33. Änderung
BAD SALZDETFURTH FLÄCHENNUTZUNGSPLAN 33. ÄNDERUNG ZUSAMMENFASSENDE ERKLÄRUNG GEMÄSS § 6 (5) BAUGB BÜRO KELLER LOTHRINGER STRASSE 15 30559 HANNOVER - 2 - Ziel und Zweck der Planung (Planungsabsicht) Die Stadt Bad Salzdetfurth hat die Aufstellung der 33. Änderung des Flächennutzungsplanes beschlossen. Die durch die Planung betroffenen Flächen waren zu einem früheren Zeitpunkt bereits Bestandteile der Planung zur 32. Flächennutzungsplanänderung im Zusammenhang mit dem Ortsteil Lechstedt. Dort wurde auch für die hier überplanten Flächen eine frühzeitige Bürger- beteiligung gemäß § 3 (1) BauGB sowie eine Beteiligung der Behörden und sonstigen Träger öffentlicher Belange gemäß § 4 (1) BauGB durchgeführt, deren Ergebnisse hier berücksichtigt werden. Der Planbereich besteht aus zwei Teilflächen im Ortsteil Groß Düngen. Der Änderungsbereich 1 befindet sich am südwestlichen Ortsrand südlich der Bundesstraße 243, der Änderungs- bereich 2 am südöstlichen Ortsrand zwischen der Wagnerstraße und der Bundesstraße 243. Eigenbedarf an Wohnbauflächen Die Stadt Bad Salzdetfurth wird im Regionalen Raumordnungsprogramm 2001 für den Land- kreis Hildesheim (RROP) als Grundzentrum in einem Ordnungsraum bezeichnet, dessen Aus- stattung mit zentralen Einrichtungen des gehobenen Bedarfs teilweise über dem Standard eines Grundzentrums liegt. In einem Ordnungsraum soll eine ausreichende Wohnraum- versorgung ermöglicht werden, die dem regionalen Wohnungsbedarf gerecht wird und die Siedlungsentwicklung mit dem Wohnungsneubau auf die zentralörtlichen Standorte und, soweit -

Haushaltsverteilung
Haushaltsverteilung Verteilgebiet: Hildesheim Landkreis/kreisfreie Stadt Postleitzahl Stadtteil/Ort Aufl age Elze 31008 Elze 2.320 Elze 31008 Esbeck 70 Elze 31008 Mehle 555 Elze 31008 Sehlde 200 Elze 31008 Sorsum 120 Elze 31008 Wittenburg 40 Elze 31008 Wülfi ngen 270 Gronau 31028 Dötzum 45 Gronau 31029 Gronau 2.245 Banteln 31029 Banteln 660 Betheln 31032 Betheln 420 Betheln 31032 Eddinghausen 50 Betheln 31032 Haus Escherde 20 Brüggen 31033 Brüggen 460 Despetal 31035 Barfelde 300 Despetal 31035 Eitzum 250 Despetal 31035 Nienstedt 66 Eime 31036 Deilmissen 120 Eime 31036 Deinsen 115 Eime 31036 Dunsen 23 Eime 31036 Eime 935 Eime 31036 Heinsen 17 Rheden 31039 Heinum 60 Rheden 31039 Rheden 225 Rheden 31039 Wallenstedt 140 Alfeld 31061 Alfeld 6.204 Alfeld 31061 Brunkensen 400 Alfeld 31061 Dehnsen 300 Alfeld 31061 Eimsen 310 Alfeld 31061 Föhrste 465 Alfeld 31061 Godenau 122 Alfeld 31061 Gerzen 489 Alfeld 31061 Hörsum 290 Alfeld 31061 Imsen 140 Alfeld 31061 Langenholzen 566 Alfeld 31061 Limmer 340 Alfeld 31061 Lütgenholzen 20 Alfeld 31061 Röllinghausen 116 Alfeld 31061 Sack 250 Alfeld 31061 Warzen 200 Alfeld 31061 Wettensen 42 Alfeld 31061 Wispenstein 140 Adenstedt 94065 Adenstedt 290 Adenstedt 94065 Grafelde 110 Adenstedt 94065 Sellenstedt 100 Haushaltsverteilung Landkreis/kreisfreie Stadt Postleitzahl Stadtteil/Ort Aufl age Almstedt 31079 Almstedt 350 Almstedt 31079 Segeste 100 Eberholzen 31079 Eberholzen 265 Sibbesse 31079 Hönze 200 Sibbesse 31079 Möllensen 60 Sibbesse 31079 Petze 250 Sibbesse 31079 Sibbesse 925 Westfeld 31079 Westfeld 235 Westfeld -

Wissenswertes Zu Fahrpreisen, Tarifen Und Angebot
BahnCard Internetadressen: Für Bahnfahrten zwischen Hildesheim und Bodenburg ROSA gilt die BahnCard im Niedersachsentarif wie auf allen www.rosa-hildesheim.de Bahnstrecken. Dadurch ist bspw. die Weiterfahrt im Niedersachsentarif Stadtgebiet Bad Salzdetfurth bzw. Hildesheim mit dem www.niedersachsentarif.de Bus enthalten („Anschlussmobilität“). Für Fahrten mit Bad Salzdetfurth dem Zug bieten die BahnCard 25 und 50 entsprechende www.bad-salzdetfurth.de Ermäßigungen auf Einzelfahrkarten. Bei ROSA wird die PRO BAHN BahnCard nicht anerkannt. www.pro-bahn.de/braunschweig-hildesheim Besonderer Tipp für Jugendliche: Sie erhalten für eine Nordwestbahn-Agentur einmalige Zahlung von 10 Euro eine BahnCard 25, die uneingeschränkt bis zum Alter von 18,99 Jahren Im KulturBahnhof Bad Salzdetfurth gültig ist. (Mo – Fr von 06.50 – 11.15 Uhr und 13.50 – 16.25 Uhr). Nachtsbus Fahrkarten per App Der Nachtsbus bietet am späten Abend in der Nacht Ticketkauf im Niedersachsentarif über auf Samstag und Sonntag ein kreisweites Busangebot. die App „FahrPlaner“. Alle Fahrkarten von ROSA sowie das Niedersachsen- ticket werden im Nachtsbus anerkannt. Ab Hildesheim starten die Busse der Linie N7 um 23.00 Uhr, 1.00 Uhr, Wissenswertes 2.35 Uhr und 4.00 Uhr. Es bestehen attraktive An- schlüsse von der S-Bahn aus Richtung Hannover. Gegen Mitternacht gibt es zudem in der Gegenrichtung zu Fahrpreisen, eine Verbindung nach Hildesheim. Hildesheim Hbf Hildesheim Ost Tarifen und Angebot Anruf-Linientaxi (ALT) Das Anruf-Linientaxi ist eine Fahrgastbeförderung mit Bad Salzdetfurth Mitte/Süd Taxis, die nur von gekennzeichneten Abfahrtsstellen Lechstedt und nur zu bestimmten Zeiten durchgeführt wird. Heinde Fahrgastverband Die Beförderung erfolgt nach vorheriger Anmeldung, Listringen PRO BAHN die bis zu 60 Minuten vor der Abfahrt unter der Groß Düngen Telefonnummer 05121 / 7642-0 erledigt sein muss. -

ST. GALLUS Bad Salzdetfurth PFARR- INFO
Gottesdienste und Veranstaltungen der kath. Pfarrgemeinde PFARR- ST. GALLUS Bad Salzdetfurth INFO Nr. 3/2021 vom 27.2.2021 bis 28.03.2021 27.03. Samstag 07.03. 3. Fastensonntag 18:00 Hl. Messe (Pfr. B.) Kollekte f. Aufgaben der Ehe- und St. Cosmas und Damian - Groß Düngen Familienpastoral + Helene Vollmer 10:30 Familienmesse (Pfr. S.) Hl. Familie - Bad Salzdetfurth 28.03. 2. Fastensonntag Gemeindekollekte 08.03. Montag 09:00 Hl. Messe (Pfr. B.) 17:15 Rosenkranzgebet St. Gallus – Detfurth Schönstattkapelle - Detfurth + Hildegard Remmert 09.03. Dienstag 10:30 Hl. Messe (Pfr. S.) St. Mariä Himmelfahrt – Westfeld 09:00 Hl. Messe St. Mariä Himmelfahrt - Westfeld 01.03. Montag 17:15 Rosenkranzgebet 11.03. Donnerstag Schönstattkapelle - Detfurth 09:00 Hl. Messe St. Johannes Evangelist – Hockeln 02.03. Dienstag + Michael Ptak 09:00 Hl. Messe 17:15 Rosenkranzgebet – St. Mariä Himmelfahrt Westfeld Schönstattkapelle - Detfurth 09:00 Hl. Messe St. Gallus - Detfurth 12.03. Freitag 09:00 Hl. Messe 03.03. Mittwoch St. Johannes Enthauptung - Wesseln 09:00 Hl. Messe St. Gallus - Detfurth 13.03. Samstag 18:00 Hl. Messe (Pfr. B.) 04.03. Donnerstag St. Mariä Himmelfahrt – Westfeld 09:00 Hl. Messe St. Johannes Evangelist – Hockeln 14.03. 4. Fastensonntag + Siegfried Schrader Gemeindekollekte 09:00 Hl. Messe (Pfr. B.) 17:15 Rosenkranzgebet St. Gallus – Detfurth Schönstattkapelle - Detfurth ++ Elisabeth v. Hermanni u. Eltern 05.03. Freitag + Karl Heinrich Bögershausen 09:00 Hl. Messe 10:30 Hl. Messe (Pfr. S.) St. Johannes Enthauptung - Wesseln Hl. Familie - Bad Salzdetfurth 06.03. Samstag 15.03. Montag 18:00 Hl. Messe (Pfr. S.) 17:15 Rosenkranzgebet St. -

Wissenswertes Zu Fahrpreisen, Tarifen Und Angebot
BahnCard Internetadressen: Bei ROSA wird die BahnCard nicht anerkannt. Für ROSA Bahnfahrten zwischen Hildesheim und Bodenburg gilt www.rosa-hildesheim.de sie aber im Niedersachsentarif wie auf allen Bahn- Niedersachsentarif strecken. Dadurch ist bspw. die Weiterfahrt im Stadt- www.niedersachsentarif.de gebiet Bad Salzdetfurth bzw. Hildesheim mit dem Bus Bad Salzdetfurth enthalten („Anschlussmobilität“). Für Fahrten mit dem www.bad-salzdetfurth.de Zug bieten die BahnCard 25 und 50 entsprechende PRO BAHN Ermäßigungen auf Einzelfahrkarten. www.pro-bahn.de/braunschweig-hildesheim Besonderer Tipp für Jugendliche: Sie erhalten für eine Nordwestbahn-Agentur einmalige Zahlung von 10 Euro eine BahnCard 25, die uneingeschränkt bis zum Alter von 18,99 Jahren Im KulturBahnhof Bad Salzdetfurth gültig ist. (Mo – Fr von 06.50 – 11.15 Uhr und 13.50 – 16.25 Uhr). Nachtsbus Der Nachtsbus bietet am späten Abend in der Nacht auf Samstag und Sonntag ein kreisweites Busangebot. Alle Fahrkarten von ROSA sowie das Niedersachsen- ticket werden im Nachtsbus anerkannt. Ab Hildesheim starten die Busse der Linie N6 um 23.00 Uhr, 1.00 Uhr, Wissenswertes 2.35 Uhr und 4.00 Uhr. Es bestehen attraktive An- schlüsse von der S-Bahn aus Richtung Hannover. Gegen Mitternacht gibt es zudem in der Gegenrichtung zu Fahrpreisen, eine Verbindung nach Hildesheim. Hildesheim Hbf Hildesheim Ost Tarifen und Angebot Anruf-Linientaxi (ALT) Das Anruf-Linientaxi ist eine Fahrgastbeförderung mit Bad Salzdetfurth Nord Taxis, die nur von gekennzeichneten Abfahrtsstellen Lechstedt und nur zu bestimmten Zeiten durchgeführt wird. Heinde Fahrgastverband Die Beförderung erfolgt nach vorheriger Anmeldung, Listringen PRO BAHN die bis zu 60 Minuten vor der Abfahrt unter der Groß Düngen Telefonnummer 05121 / 7642-0 erledigt sein muss. -
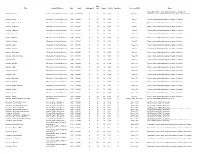
Um-Maps---G.Pdf
Map Title Author/Publisher Date Scale Catalogued Case Drawer Folder Condition Series or I.D.# Notes Topography, towns, roads, political boundaries for parts of Gabon - Libreville Service Géographique de L'Armée 1935 1:1,000,000 N 35 10 G1-A F One sheet Cameroon, Gabon, all of Equatorial Guinea, Sao Tomé & Principe Gambia - Jinnak Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 1 Towns, roads, political boundaries for parts of Gambia Gambia - N'Dungu Kebbe Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 2 Towns, roads, political boundaries for parts of Gambia Gambia - No Kunda Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 4 Towns, roads, political boundaries for parts of Gambia Gambia - Farafenni Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 5 Towns, roads, political boundaries for parts of Gambia Gambia - Kau-Ur Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 6 Towns, roads, political boundaries for parts of Gambia Gambia - Bulgurk Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 6 A Towns, roads, political boundaries for parts of Gambia Gambia - Kudang Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 7 Towns, roads, political boundaries for parts of Gambia Gambia - Fass Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 7 A Towns, roads, political boundaries for parts of Gambia Gambia - Kuntaur Directorate of Colonial Surveys 1948 1:50,000 N 35 10 G1-B G Sheet 8 Towns, roads, political -

Landschaftsästhetisches Gutachten
Werkstatt für Landschafts- u. Freiraumentwicklung, Dr. W. Nohl, 85551 Kirchheim b. München Werkstatt für Landschafts- Stockäckerring 17 und Freiraumentwicklung 85551 Kirchheim Dr. Werner Nohl Tel (089) 903 83 46 Honorarprofessor (TU München) Fax (089) 904 58 05 Landschaftsästhetische Auswirkungen der geplanten Windfarm im Büntetal auf den Landschaftsraum der Mittleren Innerste Gutachten Werner Nohl Kirchheim, im Juni 2003 Werkstatt für Landschafts- u. Freiraumentwicklung, Dr. W. Nohl, 85551 Kirchheim b. München Landschaftsästhetische Auswirkungen der geplanten Windfarm im Büntetal auf den Land- schaftsraum der Mittleren Innerste Gutachten Werner Nohl Im Auftrag der Bürgerinitiative „Rettet die Bünte“ e.V., Bad Salzdetfurth Kirchheim, im Juni 2003 Werkstatt für Landschafts- und Stockäckerring 17 Freiraumentwicklung D-85551 Kirchheim bei München Dr. Werner Nohl Tel. (089) 903 83 46 Honorarprofessor (TU München) Fax (089) 904 58 05 [email protected] www.landschaftswerkstatt.de Werkstatt für Landschafts- u. Freiraumentwicklung, Dr. W. Nohl, 85551 Kirchheim b. München GLIEDERUNG Seite 1. Anlass des Gutachtens und Vorgehensweise 1 1.1 Anlass 1 1.2 Vorgehensweise 1 2. Beschreibung der geplanten Windfarm und möglicher land- schaftsästhetischer Auswirkungen 2 2.1 Beschreibung wichtiger Gestaltaspekte 2 2.2 Mögliche landschaftsästhetische Auswirkungen 2 3. Der landschaftsästhetische Wirkraum der geplanten Windfarm im Büntetal – Unterteilung und Abgrenzungen 4 3.1 Abgrenzung des psychologischen Wirkraums 4 3.2 Abgrenzung des visuellen Wirkraums 4 4. Naturschutzrechtlich besonders geschützte Bereiche im landschafts- ästhetischen Wirkraum 6 5. Beurteilung der ästhetischen Qualität der Landschaft in den beiden Wirkräumen 8 5.1 Hinweise zum Landschaftsbild im psychologischen Wirkraum 8 5.2 Ästhetische Bewertung der Landschaft im psychologischen Wirkraum 11 5.3 Hinweise zum Landschaftsbild im visuellen Wirkraums 12 5.4 Ästhetische Bewertung der Landschaft im visuellen Wirkraum 15 6. -

Hebammenliste März 2015-2
Freiberuflich tätige Hebammen im Landkreis Hildesheim: Name Straße Ort Telefon Mobil Al-Khatib, Kerstin Kurt-Schumacher-Str. 79 31139 Hildesheim (05121) 2 66 734 0171 / 373 31 82 Geburtsvorbereitung Schwangerenvorsorge Wochenbettnachsorge energetische Massagen im Wochenbett Rückbildung Althaus, Inka Zierenbergstr. 94 31137 Hildesheim (05121) 9 18 93 56 Betreuung in der Schwangerschaft außerklinische Geburtshilfe Wochenpflege Alves Monteiro, Elisabeth Im Ehmken 63 31162 Bad Salzdetfurth (OT Heinde) (05064) 8 50 58 Schwangerenberatung Geburtsvorbereitung Wochenbettnachsorge Brönnecke, Katrin Wilhelm-Busch-Str. 3 31191 Algermissen (05126) 20 08 Geburtsvorbereitung Wochenbettnachsorge Busche, Franziska Langer Hagen 26 31134 Hildesheim (0163) 2183833 Schwangerenberatung Wochenbettbetreuung Kurse: - Geburtsvorbereitung - Rückbildung Collier, Tanja Siedlung Leinetal 6b 37547 Kreiensen (05563) 99 93 29 Schwangerenberatung Wochenbettpflege Kurse (in Seesen): - Geburtsvorbereitung - Rückbildung Dörrie-Sue, Manuela Winzenburger Str. 65 31065 Alfeld (05065) 88 17 Schwangerenbetreuung Wochenpflege Fischer, Ruth Schuhstr. 11 31162 Bad Salzdetfurth (05064) 96 23 32 Schwangerenbetreuung Geburtsvorbereitung Wochenbettnachsorge Gabloffsky, Luise Kantstr. 5 31171 Nordstemmen-Rössing (05066) 60 39 10 0172 / 99 45 404 Betreuung in der Schwangerschaft Wochenpflege Rückbildungsgymnastik Hamdusch, Inna Saarstr. 89 31141 Hildesheim 0174 / 52 90 777 WochenbettbetreuungSchwangerenschwimmen Akupunktur Hermann-Wilkening, Bianka Mellingerstr. 32 31141 Hildesheim (05121) -

Nachtsbus.De Bus Zum Ende
Bus zum Ende der Nacht nachtsbus.de Der Nachtverkehr ist ein Service-Angebot des Regionalverkehrs Hildesheim in Kooperation mit der Firma Rizor Omnibusverkehr GmbH im Auftrag des Landkreises Hildesheim. Der Fahrpreis entspricht den jeweiligen Tarifen der Busunternehmen. Gruppen bis 5 Personen können kostengünstig mit dem „Gruppenticket” fahren. v¶ Busausstieg R Rückfahrt, Haltestellen werden teilweise in anderer Reihenfolge bedient • Gültig ab 01.02.2016 jeweils Freitag und Samstag • alle Angaben sind ohne Gewähr • Bilder: www.fotolia.de Abfahrtszeiten N1 Hildesheim - Giesen - Sarstedt N2 Hildesheim - Harsum - Algermissen - Groß Lobke N3 Hildesheim - Adlum - Hohenhameln N4 Hildesheim - Schellerten - Groß Lafferde N5 Hildesheim - Söhlde N6 Hildesheim - Holle N7 Hildesheim - Bodenburg - Westfeld N7 Bad Salzdetfurth - Bockenem - Lamspringe - Sehlem N8 Hildesheim - Diekholzen - Sibbesse N9 Hildesheim - Nordstemmen - Elze - Gronau Hbf/ZOB Hildesheim 23:00 1:00 2:30 4:00 N1 Hildesheim - Giesen - Sarstedt Hildesheim/Theaterstraße 22:55 0:55 2:25 3:55 Hildesheim/Hbf - ZOB 23:00 1:00 2:30 4:00 Hildesheim/Richthofenstraße 23:04 1:04 2:34 4:04 Steuerwald/Kreisberufsschule 23:05 1:05 2:35 4:05 Hasede/Mitte 23:09 1:09 2:39 4:09 Hasede/Scharfe Ecke 23:11 1:11 2:41 4:11 Giesen/Gastw. Ernst 23:12 1:12 2:42 4:12 Giesen/Rathaus 23:13 1:13 2:43 4:13 Giesen/Molkerei 23:14 1:14 2:44 4:14 Ahrbergen/Süd 23:17 1:17 2:47 4:17 Ahrbergen/Ost 23:18 1:18 2:48 4:18 Ahrbergen/Nord 23:19 1:19 2:49 4:19 Sarstedt/Ziegelei 23:22 1:22 2:52 4:22 Sarstedt/Am Ried 23:23 1:23 2:53 4:23 Sarstedt/Wendeschleife 23:24 1:24 2:54 4:24 Sarstedt/Wendeschleife 23:30 1:30 3:00 4:30 Sarstedt/Am Ried 23:32 1:32 3:02 4:32 Sarstedt/Ziegelei 23:33 1:33 3:03 4:33 Ahrbergen/Nord 23:36 1:36 3:06 4:36 Ahrbergen/Ost 23:37 1:37 3:07 4:37 Ahrbergen/Süd 23:39 1:39 3:09 4:39 Giesen/Molkerei 23:42 1:42 3:12 4:42 Giesen/Rathaus 23:43 1:43 3:13 4:43 Giesen/Gastw. -

SK FB Orthopaedie 2019-10.Indd
Sich rundum wohlfühlen Willkommmen in der MEDIAN Salze Klinik Bad Salzdetfurth Unsere Patienten wohnen in komfortablen Einzel Ärztliche Leitung und Kontakt zimmern mit Dusche, Telefon und KabelTV. Die Fachklinik für orthopädische und psycho Dr. med. Marian Fritzen, Chefärztin Orthopädie Zimmer sind überwiegend mit Balkon ausgestattet. Fachärztin für Orthopädie und Unfallchirurgie, somatische Rehabilitation Um Ihren Klinikaufenthalt so abwechslungsreich und Spezielle Orthopädische Chirurgie, Chirotherapie, interessant wie möglich zu gestalten, sind Sie herz zertifizierte Fußchirurgin D.A.F. e.V., Sozialmedizin Liebe Patientin, lieber Patient, lich zu regelmäßig stattfindenden Freizeitaktionen Dr. med. Andreas Weiß, Ltd. Oberarzt eingeladen. Sie kennen das: Der Rücken schmerzt, das Knie Facharzt für Orthopädie, Physikalische und bereitet Probleme, das Ziehen in der Schulter wird Rehabilitative Medizin, Chirotherapie, Für die Zeit nach den Therapien bietet der Kurpark immer unangenehmer und je älter man ist, desto Physikalische Therapie, Sozialmedizin mit seinem über 250 Jahre alten Gradierwerk, den schwerer fällt es, nach einer Akutbehandlung die Pavillons und dem Parkcafé eine erholsame Idylle. Zentraler Reservierungsservice alte Beweglichkeit wieder zurückzuerlangen und Leitung Tobias Heinrich · Anmeldung & Aufnahme möglichst schmerzfrei zu werden. Dazu kommen T +49 (0)5222 373737 · F +49 (0)5222 373744 Bad Salzdetfurth ist mit seinen zahlreichen alten die vielen chronischen Erkrankungen, die mit zu reservierungsservice.badsalzdetfurth@ Fachwerkhäusern und hübschen Geschäften ein nehmendem Lebensalter auftreten oder manchen mediankliniken.de attraktives Ausflugsziel. Das Städtchen mit dem schon ein Leben lang begleiten. In jedem Fall, auch anmutigen Flair besitzt ein eigenes, staatlich bei jüngeren Patienten, ist eine fachgerechte anerkanntes Moor und Soleheilbad. Rehabilitation wichtig, um wieder „auf die Beine“ Richtung Hamburg zu kommen. -

Lammetalbahn Unterwegs Im Auftrag Von
Fahrplan 2020 RB 79 Lammetalbahn Unterwegs im Auftrag von: Landesnahverkehrsgesellschaft Niedersachsen mbH www.lnvg.de Hildesheim Hbf Bad Salzdetfurth Nahverkehr Westfalen-Lippe (NWL) Bodenburg www.nwl-info.de Gültig ab 15.12.2019 twitter.com/nwb_nds facebook.com/nordwestbahn RB 79 Fahrplan 2020 Montag bis Freitag RB 79 Hildesheim Hbf › Bodenburg RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 RB 79 Zugnummer 82891 82893 82895 82899 82901 82903 82905 82907 82909 82911 82913 82915 82917 82919 82921 82923 82925 82927 82929 RB 79 Hildesheim Hbf ab 05:34 06:34 07:06 07:56 08:34 09:34 10:34 11:34 12:34 13:34* 14:34 15:34 16:34 17:34 18:34 19:34 20:34 21:37 22:37 Hildesheim Ost ab 05:38 06:38 07:10 08:00 08:38 09:38 10:38 11:38 12:38 13:38* 14:38 15:38 16:38 17:38 18:38 19:38 20:38 21:41 22:41 Groß Düngen ab 05:44 06:44 07:16 08:06 08:44 09:44 10:44 11:44 12:44 13:44* 14:44 15:44 16:44 17:44 18:44 19:44 20:44 21:47 22:47 Wesseln ab 05:48 06:48 07:21 08:10 08:48 09:48 10:48 11:48 12:48 13:48* 14:48 15:48 16:48 17:48 18:48 19:48 20:48 21:51 22:51 Bad Salzdetfurth Solebad ab 05:51 06:51 07:25 08:14 08:51 09:51 10:51 11:51 12:51 13:51* 14:51 15:51 16:51 17:51 18:51 19:51 20:51 21:54 22:54 Bad Salzdetfurth ab 05:53 06:53 07:27 08:16 08:53 09:53 10:53 11:53 12:53 13:53* 14:53 15:53 16:53 17:53 18:53 19:53 20:53 21:56 22:56 Bodenburg an 05:57 06:57 07:32 08:20 08:57 09:57 10:57 11:57 12:57 13:57* 14:57 15:57 16:57 17:57 18:57 19:57 20:57 22:00 23:00 * Nur 2. -

Freitags Der Rufbus Kommt!
Der Rufbus kommt! - Anruf unter 05063/2222 an Werktagen montags - freitags Fahrt Nr. 2 6 12a 16 20 Fahrt Nr. 1 9 15 21 Bemerkungen üb. Segeste Bemerkungen Anschl. Zug aus Ri. Hildesheim - 08:55 - 16:55 Bad Salzdetfurth - Bahnhof 10:32 13:40 Bad Salzdetfurth - Bahnhof I 09:08 I 17:06 Bad Salzdetfurth Neuer Krug 10:34 13:42 Bad Salzdetfurth Neuer Krug I 09:11 I 17:08 Bad Salzdetfurth Klusbrücke 10:35 13:43 Bad Salzdetfurth Klusbrücke I 09:12 I 17:09 Maiental I 13:45 Anschl. Zug aus Ri. Hildesheim 06:56 08:59 13:59 16:59 Wehrstedt Ahnepaule 10:36 13:48 Bodenburg - Bahnhof 07:00 09:15 14:01 17:12 Wehrstedt Schmiede 10:38 13:50 Evensen 07:04 09:19 14:19 17:16 Anschl. Zug aus Ri. Hildesheim - 13:59 17:59 Wöllersheim 07:08 09:23 14:23 17:20 Bodenburg - Bahnhof 10:42 14:01 18:02 Neuhof 07:11 09:26 14:26 17:23 Östrum 10:44 | | Lamspringe (1) 07:15 09:30 14:30 17:27 Breinum Hüttenstraße 10:46 | | Ammenhausen, Hornsen, 9:30 14:30 17:27 Almstedt 10:48 14:07 18:08 Glashütte (2) 9:35 14:35 17:32 Lamspringe (1) 07:15 09:40 14:40 17:37 Segeste 10:51 14:10 18:11 Neuhof 07:19 09:44 14:44 17:41 Wöllersheim 07:22 09:47 14:47 17:44 Segeste 06:45 10:51 14:10 Evensen 07:26 09:51 14:51 17:48 Almstedt 06:48 10:54 14:13 Almstedt I I I 17:57 Breinum Hüttenstraße 06:50 10:56 14:15 Breinum Hüttenstraße I I I 17:59 Östrum 06:52 10:58 weiter Östrum I I I 18:00 Bodenburg - Bahnhof 06:55 11:00 nach Bodenburg - Bahnhof 07:32 09:57 14:55 18:02 Anschl.