DOCSLIB.ORG

©Copyright 2015 Shaowu Huang

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
©Copyright 2015 Shaowu Huang ©Copyright 2015 Shaowu Huang Broadband Green’s Function and Applications to Fast Electromagnetic Analysis of High-Speed Interconnects Shaowu Huang A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Washington 2015 Reading Committee: Leung Tsang, Chair Henning Braunisch Kung-Hau Ding Yasuo Kuga Program Authorized to Offer Degree: Electrical Engineering University of Washington Abstract Broadband Green’s Function and Applications to Fast Electromagnetic Analysis of High-Speed Interconnects Shaowu Huang Chair of the Supervisory Committee Professor Leung Tsang Department of Electrical Engineering This dissertation is focused on research and development of an innovative Broadband Green’s Function method and the applications to fast electromagnetic modeling and simulations of high-speed interconnects. Innovative solutions based on proposed broadband Green’s function method are presented and demonstrated to solve the challenging problems in signal integrity, power integrity, and electromagnetic compatibility and interference for computer system designs. The main contents of this dissertation are twofold: to overcome the fundamental restrictions in the conventional Green’s function methods through introducing the broadband Green’s function method, to explore the applications of the broadband Green’s function to modeling of high-speed interconnects in modern electronic devices and systems. In the first project, the method of broadband Green’s function with low wavenumber extraction (BBGFL) is proposed for arbitrary shaped waveguide. The methodologies of BBGFL are derived for both Neumann and Dirichlet boundary conditions. In the second project, we combine the BBGFL with method of moment (MoM) for fast full wave modeling and simulations of scattering in arbitrary shaped waveguides. The method is applied to solve the problem of vias inside PCB power/ground plane waveguide. In the third project, a number of applications are investigated, including modeling of vias in arbitrary shaped power/ground planes, modeling of emissions from printed circuit boards, modeling of stripline connecting transition vias in power/ground planes, modeling of arbitrary shaped waveguide structures in microwave components. The proposed methods are compared to in-house method of moment program and commercial HFSS tool. Simulation results of various problems are illustrated. The present methods are verified by comparing the resonant frequencies, Green’s functions, S-parameters, surface fields, and/or radiated emission for different problems. BBGFL has good agreement with MoM and/or HFSS on the numerical results. The computational efficiency is checked by comparing the CPU time. BBGFL is about two or three orders faster than MoM and HFSS for most cases in modeling of high-speed interconnects. TABLE OF CONTENTS Chapter 1 Introduction .................................................................................................... 1 1.1 Research Background.......................................................................................... 1 1.2 Research Methodology ....................................................................................... 2 1.3 Organization of the Dissertation ......................................................................... 4 Chapter 2 Broadband Green's Function with Low Wavenumber Extraction Method for Arbitrary Shaped Waveguides: TE case and Application to Modelling of Vias in Finite Power/Ground Plane .......................................................................................................... 9 2.1 Summery ............................................................................................................. 9 2.2 Introduction ........................................................................................................ 9 2.3 Methodology ..................................................................................................... 12 Broadband Bounded Green’s Function with Low Frequency Extractions for Neumann Case .................................................................................................... 12 2.3.1.1 Broadband Green’s Function and with Low Wavenumber Extraction. ..............................................................................., , , , ....... 13 2.3.1.2 Calculation of Modal Solution and Resonant , , Wavenumber ................................................................................................... 15 2.3.1.3 Normalization of Modes for Neumann Case ........................................ 18 2.3.1.4 Broadband Green’s Function for L-shaped Waveguide and Low Wavenumber Extraction ....................................................................................... 21 2.3.1.5 Summary Procedure for Computing ................................ 22 , , Application of Broadband Green’s Function of Arbitrary Waveguide to Foldy Lax Multiple Scattering Equation for Scattering by Vertical Vias .................... 24 Small Patch Green’s Function for TE Case ................................................ 29 2.3.3.1 Small Patch Integrated Green’s Function for TE Case .......................... 30 2.3.3.2 Derivative of Small Patch Integrated Green’s Function for TE Case ..... 31 2.4 Numerical Results ............................................................................................. 35 i Computation of Green’s Functions for Neumann Case ............................ 35 2.4.1.1 Resonant Wavenumber Comparison .................................................... 35 2.4.1.2 Modal Solution Comparison ................................................................. 37 2.4.1.3 Comparison of Green’s Function .................................................... 39 2.4.1.4 Comparison of CPU Times ..................................................................... 41 Application of BBGFL to the Simulation of Vias in Arbitrarily Shaped PCB Power/Ground Plane Pair ......................................................................................... 43 2.4.2.1 Modeling of Two Signal Vias in a Rectangular Power/Ground Plane Pair with Small Cut Out ................................................................................................ 43 2.4.2.2 Modeling of Two Signal Vias in A Rectangular Power/Ground Plane Pair with Large Cut Out ................................................................................................ 46 2.4.2.3 Modeling of Two Signal Vias and Two Shorting Vias in a Rectangular Power/Power (or Ground/Ground) Plane Pair with Large Cut Out ...................... 49 2.4.2.4 Modeling of 8 Vias: Four Signal Vias and Four Shorting Vias in a Rectangular Power/Power (or Ground/Ground) Plane Pair with Large Cut Out .. 52 2.4.2.5 Comparison of CPU Time for Vias Simulations ..................................... 55 2.5 Conclusion ......................................................................................................... 56 Chapter 3 Fast Electromagnetic Analysis of Emissions from Printed Circuit Board Using Broadband Green’s Function ............................................................................................ 57 3.1 Summary ........................................................................................................... 57 3.2 Introduction ...................................................................................................... 57 3.3 Methodology ..................................................................................................... 60 Broadband Green’s Function with Low Wavenumber Extraction for Calculation of Fields on Boundary Walls of Power/Ground Plane ........................... 61 Calculation of Radiated Emissions From Power/Ground Plane with Green’s Functions .................................................................................................... 64 3.4 Simulation ......................................................................................................... 67 Case A: 0.5 by 0.5 Square-inch Rectangular Power/Ground Plane Pair with 0.125 by 0.35 Square-inch Cut-out ................................................................... 68 Case B: 1.5 by 1.5 Square-inch Rectangular Power/Ground Plane Pair with 0.125 by 0.35 Square-inch Cut-out ................................................................... 72 ii Case C: 5 by 5 Square-inch Rectangular Power/Ground Plane Pair with 0.125 by 0.35 Square-inch Cut-out ........................................................................... 75 Case D: 5 by 5 Square-inch Rectangular Power/Ground Plane Pair with 1.25 by 3.5 Square-inch Cut-out ............................................................................... 78 Case E: 0.5 by 0.5 Square-inch Rectangular Power/Ground Plane Pair with 0.1 by 0.1 Square-inch Cut-out ......................................................................... 81 Case F: 1 by 1 Square-inch Rectangular Power/Ground Plane Pair with 0.125 by 0.35 Square-inch Cut-out ........................................................................... 85 Comparison of CPU Time for Vias Simulations ......................................... 88 3.5 Conclusion ......................................................................................................... 90 Chapter 4 Combining Broadband Green's Function with Low Wavenumber Extraction and Method of Moment for Fast Broadband Simulations of Scattering in Arbitrary Shaped Waveguides .........................................................................................................
Load more

Recommended publications
  • American Protestant Female Medical Missionaries to China, 1880-1930
    W&M ScholarWorks Undergraduate Honors Theses Theses, Dissertations, & Master Projects 5-2020 Imperial Professionals: American Protestant Female Medical Missionaries to China, 1880-1930 Yutong Zhan William & Mary Follow this and additional works at: https://scholarworks.wm.edu/honorstheses Part of the Cultural History Commons, Social History Commons, United States History Commons, and the Women's History Commons Recommended Citation Zhan, Yutong, "Imperial Professionals: American Protestant Female Medical Missionaries to China, 1880-1930" (2020). Undergraduate Honors Theses. Paper 1530. https://scholarworks.wm.edu/honorstheses/1530 This Honors Thesis is brought to you for free and open access by the Theses, Dissertations, & Master Projects at W&M ScholarWorks. It has been accepted for inclusion in Undergraduate Honors Theses by an authorized administrator of W&M ScholarWorks. For more information, please contact [email protected]. Imperial Professionals: American Protestant Female Medical Missionaries to China, 1880-1930 A thesis submitted in partial fulfillment of the requirement for the degree of Bachelor of Arts in History from The College of William and Mary by Yutong Zhan Accepted for Highest Honors (Honors, High Honors, Highest Honors) Adrienne Petty, Director Joshua Hubbard Leisa Meyer Williamsburg, VA May 1, 2020 Table of Contents Acknowledgements ……………………………………………………………………………...2 Illustrations ………………………………………………………………………………………3 Introduction………………………………………………………………………………………5 Chapter I. “The Benefit of [...] the Western World”:
    [Show full text]
  • Climate Warming and Sea Level Rise
    Climate warming and sea level rise. Item Type Journal Contribution Authors Yue, Jun; Dong, Yue; Wu, Sangyun; Geng, Xiushan; Zhao, Changrong Citation Marine Science Bulletin, 14 (1), 28-41 Download date 29/09/2021 06:19:22 Item License http://creativecommons.org/licenses/by-nc/3.0/ Link to Item http://hdl.handle.net/1834/5832 Vol. 14 No. 1 Marine Science Bulletin May 2012 Climate warming and sea level rise YUE Jun1, 2, 3, Dong YUE4, WU Sang-yun5, GENG Xiu-shan5, ZHAO Chang-rong2 1. Tianjin Marine Geology Exploration Center, Tianjin 300170, China; 2. Tianjin Institute of Geology and Mineral Resources, CGS, Tianjin 300170, China; 3. Geological Research Institute of North China Geological Exploration Bureau, Tianjin 300170, China; 4. University of Texas at San Antonio (Texas 78249-1644 USA); 5. First Institute of Oceanography, SOA, Qingdao 266061, Shandong Province, China Abstract: Based on a large number of actual data, the author believe that the modern global warming and sea level rise resulted from climate warming after the cold front of the Little Ice Age about 200 years ago and the developmnet of the sea level rise phase. In the past 30 years, the rate of sea level rise was increasing, which is under the background of the average temperature uplift 0.2F°(0.11 °C)every 10 years in succession from the 1980s to the past 10 years this century. On the basis of the absolute and relative sea-level rise rate that was calculated from the tidal data during the same period at home and abroad in the last 30 years, in accordance with the resolutions of the 2010 climate conference in Cancun, at the same time, considering the previous prediction and research, the world’s sea levels and the relative sea level in Tianjin, Shanghai, Dongying, Xiamen, Haikou and other coastal cities that have severe land subsidence in 2050 and 2100 are calculated and evaluated.
    [Show full text]
  • (51) International Patent Classification: Road, Jin Tang Industry Park, Shaowu, Nanping, Fujian 354003 (CN). WU, Wenting; ZHANG
    ( (51) International Patent Classification: Road, Jin Tang Industry Park, Shaowu, Nanping, Fujian C07C 25/13 (2006.0 1) C07C 205/12 (2006.0 1) 354003 (CN). WU, Wenting; ZHANG, Li, No.6, Jin Ling C07C 25/18 (2006.01) B01J 27/12 (2006.01) Road, Jin Tang Industry Park, Shaowu, Nanping, Fujian C07C 201/12 (2006.01) 354003 (CN). (21) International Application Number: (74) Agent: FUZHOU GEMHOPE PATENT AGENCY; PCT/CN20 19/0943 80 LIN, Xiangxiang, Room703, Building No.34, District C, Fuzhou Software Park, No. 89 Software Boulevard, Tong- (22) International Filing Date: pan Road, Gulou District, Fuzhou, Fujian 350003 (CN). 02 July 2019 (02.07.2019) (81) Designated States (unless otherwise indicated, for every (25) Filing Language: English kind of national protection av ailable) . AE, AG, AL, AM, (26) Publication Language: English AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DJ, DK, DM, DO, DZ, (30) Priority Data: EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, HN, HR, 10 2019 103 836.7 HU, ID, IL, IN, IR, IS, JO, JP, KE, KG, KH, KN, KP, KR, 15 February 2019 (15.02.2019) DE KW,KZ, LA, LC, LK, LR, LS, LU, LY, MA, MD, ME, MG, (71) Applicant: FUJIAN YONGJING TECHNOLOGY CO., MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, OM, LTD [CN/CN]; ZHANG, Li, No.6, JinLing Road, Jin Tang PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SA, SC, Industry Park, Shaowu, Nanping, Fujian 354003 (CN).
    [Show full text]
  • Checklist of Mites from Moso Bamboo in Fujian, China
    Systematic & Applied Acarology Special Publications (2000) 4, 81-92 81 Checklist of mites from moso bamboo in Fujian, China JIANZHEN LIN1, ZHI-QIANG ZHANG2, YANXUAN ZHANG1, QIAOYUN LIU3& JIE JI1 1Institute of Plant Protection, Fujian Academy of Agricultural Sciences, Fuzhou, 350013 China; e-mail [email protected] 2Landcare Research, Private Bag 92170, Auckland, New Zealand 3Laboratory of Forest Protection, Fujian Forestry Bureau, Fuzhou 350002,China Abstract This paper gives a report of 45 species of mites from the moso bamboo (Phy- llostachys pubescens) in Fujian province, China. They belong to 23 genera in 9 families. Some of the Tetranychidae (e.g. Aponychus copuzae Rimando and Schizotetranychus nanjingensis Ma et Yuan) and Eriophyidae (e.g. Aculus bambusae Kuang), either alone or in mixed populations, cause serious injury to the moso bamboo in Fujian. Key words: Acari, pest, natural enemy, bamboo, Phyllostachys pubescens. Introduction The moso bamboo, Phyllostachys pubescens, is widely distributed in areas south of Qinling mountains and Changjiang (Yangtze River) in China. It is a valuable economic crop and is widely cultivated in Hunan, Jiangxi, Zhejiang and Fujian provinces. Spider mites (Tetranychidae) are often collected on bamboo leaves in China. Wang (1981) recorded Aponychus copuzae Rimando injuring the moso bamboo in Zhejiang, Jiangxi, Taiwan, and Guangdong. Ma et al. (1984) also collected this species in Anhui and Guangxi. In addi- 82 Systematic & Applied Acarology Special Publications (2000) 4 tion, they also recorded Stylophoronychus guangzhouensis (Ma et Yuan 1980; see Zhang et al. 2000b), Schizotetranychus nanjingensis Ma et Yuan, S. bambusae Reck and Tetranychus bambusae Wang et Ma on bamboo.
    [Show full text]
  • Table of Codes for Each Court of Each Level
    Table of Codes for Each Court of Each Level Corresponding Type Chinese Court Region Court Name Administrative Name Code Code Area Supreme People’s Court 最高人民法院 最高法 Higher People's Court of 北京市高级人民 Beijing 京 110000 1 Beijing Municipality 法院 Municipality No. 1 Intermediate People's 北京市第一中级 京 01 2 Court of Beijing Municipality 人民法院 Shijingshan Shijingshan District People’s 北京市石景山区 京 0107 110107 District of Beijing 1 Court of Beijing Municipality 人民法院 Municipality Haidian District of Haidian District People’s 北京市海淀区人 京 0108 110108 Beijing 1 Court of Beijing Municipality 民法院 Municipality Mentougou Mentougou District People’s 北京市门头沟区 京 0109 110109 District of Beijing 1 Court of Beijing Municipality 人民法院 Municipality Changping Changping District People’s 北京市昌平区人 京 0114 110114 District of Beijing 1 Court of Beijing Municipality 民法院 Municipality Yanqing County People’s 延庆县人民法院 京 0229 110229 Yanqing County 1 Court No. 2 Intermediate People's 北京市第二中级 京 02 2 Court of Beijing Municipality 人民法院 Dongcheng Dongcheng District People’s 北京市东城区人 京 0101 110101 District of Beijing 1 Court of Beijing Municipality 民法院 Municipality Xicheng District Xicheng District People’s 北京市西城区人 京 0102 110102 of Beijing 1 Court of Beijing Municipality 民法院 Municipality Fengtai District of Fengtai District People’s 北京市丰台区人 京 0106 110106 Beijing 1 Court of Beijing Municipality 民法院 Municipality 1 Fangshan District Fangshan District People’s 北京市房山区人 京 0111 110111 of Beijing 1 Court of Beijing Municipality 民法院 Municipality Daxing District of Daxing District People’s 北京市大兴区人 京 0115
    [Show full text]
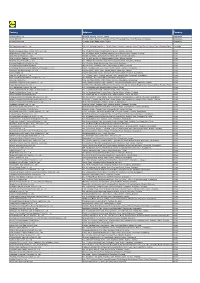
  • Factory Address Country
    Factory Address Country Durable Plastic Ltd. Mulgaon, Kaligonj, Gazipur, Dhaka Bangladesh Lhotse (BD) Ltd. Plot No. 60&61, Sector -3, Karnaphuli Export Processing Zone, North Potenga, Chittagong Bangladesh Bengal Plastics Ltd. Yearpur, Zirabo Bazar, Savar, Dhaka Bangladesh ASF Sporting Goods Co., Ltd. Km 38.5, National Road No. 3, Thlork Village, Chonrok Commune, Korng Pisey District, Konrrg Pisey, Kampong Speu Cambodia Ningbo Zhongyuan Alljoy Fishing Tackle Co., Ltd. No. 416 Binhai Road, Hangzhou Bay New Zone, Ningbo, Zhejiang China Ningbo Energy Power Tools Co., Ltd. No. 50 Dongbei Road, Dongqiao Industrial Zone, Haishu District, Ningbo, Zhejiang China Junhe Pumps Holding Co., Ltd. Wanzhong Villiage, Jishigang Town, Haishu District, Ningbo, Zhejiang China Skybest Electric Appliance (Suzhou) Co., Ltd. No. 18 Hua Hong Street, Suzhou Industrial Park, Suzhou, Jiangsu China Zhejiang Safun Industrial Co., Ltd. No. 7 Mingyuannan Road, Economic Development Zone, Yongkang, Zhejiang China Zhejiang Dingxin Arts&Crafts Co., Ltd. No. 21 Linxian Road, Baishuiyang Town, Linhai, Zhejiang China Zhejiang Natural Outdoor Goods Inc. Xiacao Village, Pingqiao Town, Tiantai County, Taizhou, Zhejiang China Guangdong Xinbao Electrical Appliances Holdings Co., Ltd. South Zhenghe Road, Leliu Town, Shunde District, Foshan, Guangdong China Yangzhou Juli Sports Articles Co., Ltd. Fudong Village, Xiaoji Town, Jiangdu District, Yangzhou, Jiangsu China Eyarn Lighting Ltd. Yaying Gang, Shixi Village, Shishan Town, Nanhai District, Foshan, Guangdong China Lipan Gift & Lighting Co., Ltd. No. 2 Guliao Road 3, Science Industrial Zone, Tangxia Town, Dongguan, Guangdong China Zhan Jiang Kang Nian Rubber Product Co., Ltd. No. 85 Middle Shen Chuan Road, Zhanjiang, Guangdong China Ansen Electronics Co. Ning Tau Administrative District, Qiao Tau Zhen, Dongguan, Guangdong China Changshu Tongrun Auto Accessory Co., Ltd.
    [Show full text]
  • Characterization of the Pathogen Causing a New Bacterial Vein Rot Disease in Tobacco in China
    Crop Protection 92 (2017) 93e98 Contents lists available at ScienceDirect Crop Protection journal homepage: www.elsevier.com/locate/cropro Short communication Characterization of the pathogen causing a new bacterial vein rot disease in tobacco in China * Jing Wang a, , 1, Yihong Wang a, 1, Tingchang Zhao b, Peigang Dai a, Xiaolong Li c a Key Laboratory of Tobacco Pest Monitoring, Controlling & Integrated Management, Qingzhou Tobacco Research of China National Corp, Institute of Tobacco, Chinese Academy of Agricultural Science, Qingdao 266101, China b State Key Laboratory for Biology of Plant Diseases and Insect Pests, Institute of Plant Protection, Chinese Academy of Agricultural Science, Beijing 10093, China c Nanping Shaowu Tobacco Company, Shaowu 354000, Fujian, China article info abstract Article history: In 2015, red or black-brown necrotic lesions on main or lateral veins associated with the wilting of leaves Received 18 September 2016 and dry rot caused by plant pathogenic bacteria were found in tobacco plants in different fields in Received in revised form Shaowu city, Fujian province, China. Two bacteria (FM3 and FM4) were isolated and selected for further 26 October 2016 tests. Pathogenicity test results showed that all the tested isolates developed typical vein rot symptoms Accepted 29 October 2016 in tobacco 4 days after inoculation and soft rot symptoms in potato tuber, okra, pepper, capsicum, celery, and Chinese cabbage 2 days after inoculation, with the bacterium re-isolated from all the inoculated plants. On the basis of phenotypic properties, maceration characteristics, biochemical tests, Biolog sys- Keywords: fi Nicotania tabacum tem, and 16S rRNA sequences analysis, isolates FM3 and FM4 were identi ed as Pectobacterium car- fi Pectobacterium carotovorum subsp.
    [Show full text]
  • 中國內地指定醫院列表 出版日期: 2019 年 7 月 1 日 Designated Hospital List in Mainland China Published Date: 1 Jul 2019
    中國內地指定醫院列表 出版日期: 2019 年 7 月 1 日 Designated Hospital List in Mainland China Published Date: 1 Jul 2019 省 / 自治區 / 直轄市 醫院 地址 電話號碼 Provinces / 城市/City Autonomous Hospital Address Tel. No. Regions / Municipalities 中國人民解放軍第二炮兵總醫院 (第 262 醫院） 北京 北京 西城區新街口外大街 16 號 The Second Artillery General Hospital of Chinese 10-66343055 Beijing Beijing 16 Xinjiekou Outer Street, Xicheng District People’s Liberation Army 中國人民解放軍總醫院 (第 301 醫院） 北京 北京 海澱區復興路 28 號 The General Hospital of Chinese People's Liberation 10-82266699 Beijing Beijing 28 Fuxing Road, Haidian District Army 北京 北京 中國人民解放軍第 302 醫院 豐台區西四環中路 100 號 10-66933129 Beijing Beijing 302 Military Hospital of China 100 West No.4 Ring Road Middle, Fengtai District 中國人民解放軍總醫院第一附屬醫院 (中國人民解 北京 北京 海定區阜成路 51 號 放軍 304 醫院） 10-66867304 Beijing Beijing 51 Fucheng Road, Haidian District PLA No.304 Hospital 北京 北京 中國人民解放軍第 305 醫院 西城區文津街甲 13 號 10-66004120 Beijing Beijing PLA No.305 Hospital 13 Wenjin Street, Xicheng District 北京 北京 中國人民解放軍第 306 醫院 朝陽區安翔北里 9 號 10-66356729 Beijing Beijing The 306th Hospital of PLA 9 Anxiang North Road, Chaoyang District 中國人民解放軍第 307 醫院 北京 北京 豐台區東大街 8 號 The 307th Hospital of Chinese People’s Liberation 10-66947114 Beijing Beijing 8 East Street, Fengtai District Army 中國人民解放軍第 309 醫院 北京 北京 海澱區黑山扈路甲 17 號 The 309th Hospital of Chinese People’s Liberation 10-66775961 Beijing Beijing 17 Heishanhu Road, Haidian District Army 中國人民解放軍第 466 醫院 (空軍航空醫學研究所 北京 北京 海澱區北窪路北口 附屬醫院） 10-81988888 Beijing Beijing Beiwa Road North, Haidian District PLA No.466 Hospital 北京 北京 中國人民解放軍海軍總醫院 (海軍總醫院） 海澱區阜成路 6 號 10-66958114 Beijing Beijing PLA Naval General Hospital 6 Fucheng Road, Haidian District 北京 北京 中國人民解放軍空軍總醫院 (空軍總醫院） 海澱區阜成路 30 號 10-68410099 Beijing Beijing Air Force General Hospital, PLA 30 Fucheng Road, Haidian District 中華人民共和國北京市昌平區生命園路 1 號 北京 北京 北京大學國際醫院 Yard No.1, Life Science Park, Changping District, Beijing, 10-69006666 Beijing Beijing Peking University International Hospital China, 東城區南門倉 5 號(西院) 5 Nanmencang, Dongcheng District (West Campus) 北京 北京 北京軍區總醫院 10-66721629 Beijing Beijing PLA.
    [Show full text]
  • Fujian (China), (Zygoptera: Calopterygoidea) Large Dragonflies
    Odonatologica33(4): 371-398 December 1, 2004 Caloptera damselflies from Fujian (China), with description of a newspecies andtaxonomic notes (Zygoptera: Calopterygoidea) M. Hämäläinen Department ofApplied Biology, P.O. Box 27, FI-00014 University ofHelsinki, Finland e-mail: [email protected] Received May 27, 2003 /Revised andAccepted March 3, 2004 Based on literature records andthe examination ofan extensive Odonata collection made in in in 21 of Fujian 1930-1940’s (now RMNH, Leiden), spp. Caloptera (Calopterygoidea) in in are recognized as occurring Fujian province eastern China. The Fujian Caloptera ma- terial (ca 860 specimens of 18 species) in RMNH is enumerated. The followingtaxonomic is from with decisions are presented: Caliphaea nitens Navas, 1934 removed synonymy Bayadera melanopteryx Ris, 1912 [!] and ranked as a valid species, distinct from C. con- similis McLachlan, 1894. The lectotype of Vestalis smaragdinaSelys, 1879 is designated. Vestalis velata 1912 V. virens is ranked while Ris, (syn. Needham, 1930) as a good species, the form of V. velata” is described “hyaline winged smaragdina (sensu Asahina, 1977) as a new sp. Vestalis venustasp. n. Bayadera continentalis Asahina, 1973 from Fujian and B. ishigakiana Asahina, 1964 from the Ryukyus are treated as full sp. and not as ssp. ofB. brevicauda Fraser, 1928 from Taiwan. Bayadera melania Navas, 1934 is synonymized with B. melanopteryx Ris, 1912. Some preliminary taxonomic comments (to be discussed in de- tail 1853 is of elsewhere) are presented: Calopteryx grandaevaSelys, a probable synonym whereas C. is Matronabasilaris C. atrataSelys, 1853, ( atrocyana (Fraser, 1935) a good sp. 1853 and M. 1879 be distinct Mnais tenuis Selys, , nigripectus Selys, appear to sp.
    [Show full text]
  • Impact of Urbanization on the Value of Ecosystem Services in Nanping City, China
    Pol. J. Environ. Stud. Vol. 30, No. 1 (2021), 965-975 DOI: 10.15244/pjoes/124175 ONLINE PUBLICATION DATE: 2020-09-18 Original Research Impact of Urbanization on the Value of Ecosystem Services in Nanping City, China Lili Zhao1,2, Xuncheng Fan1,2*, Han Lin2, Tao Hong2, Wei Hong2 1College of Urban and Rural Construction, Shaoyang University, Shaoyang, 422000 China 2Forestry College, Fujian Agriculture and Forestry University, 350002 Fuzhou, China Received: 23 April 2020 Accepted: 18 June 2020 Abstract The optimization of regional land use structures and functions and the sustainable use of the ecological environment are very important in the process of urbanization. In this study, based on the Landsat 7+ETM images of Nanping City from 2015, the object-oriented land use classification method was used to calculate the value of ecosystem services in Nanping City and various counties (districts).The spatial distribution characteristics between the levels of population urbanization, spatial urbanization, economic urbanization, and living urbanization and the value of ecosystem services were quantitatively analyzed by utilizing spatial measurement methods. The impact of the levels of four types of urbanization on the spatial distribution of ecosystem services values was explored using the bivariate spatial autocorrelation method. The results showed that there was a significant negative spatial correlation between population urbanization and the total value of ecosystem services. Specifically, the negative correlation between population urbanization
    [Show full text]
  • Overview of Fujian
    Overview of Fujian Lying in the southeastern coast of China and bordering Zhejiang Province, Jiangxi Province and Guangdong Province, Fujian is facing Taiwan across the Straits and one of the closest mainland provinces to Southeast Asia and Oceania, as well as an important window and base of China for global exchanges. Boasting a long history, Fujian was called the Region of Minyue during the Spring and Autumn Period and the Prefecture of Min-Zhong during Qing Dynasty. In the middle of Tang Dynasty, the post of Fujian Military Commissioner was established, and the province was hereafter called Fujian. The brief name of Fujian, "Min", is derived from Min River, the greatest river within the province. Covering a land area of 121,400 square kilometers and a sea area of 136,000 square kilometers, Fujian governs Fuzhou, Xiamen, Quanzhou, Zhangzhou, Putian, Longyan, Sanming, Nanping and Ningde (nine municipal cities), as well as 85 subordinated counties, cities and districts (including Jinmen County). By the end of 2005, the total population of Fujian reached 35,350,000 (exclusive of Jinmen and Mazu). As one of the earliest provinces opening to the outside world, Fujian has launched 12 national development zones and special economic zones, bringing about an all-round opening-up configuration. The people of Fujian are famed for their diligence, courage, industry and hospitality. This mountainous province is also renowned for the tradition of starting career in overseas countries, which makes it a famous hometown of overseas Chinese. Geography & Climate Located in the subtropical zone, Fujian has a moderate climate and is abundant rainfall.
    [Show full text]
  • Area B (10.2A07-12)广州交易会进出口有限公司 NINGBO CHINA-BASE LANDHAU FOREIGN TRADE CO., CANTON FAIR IMP
    第118届 第2期 the 118th session Phase 2 TEL：86-573-82117512 FAX：86-573-82117020 家具 URL：WWW.CHINAEXPORTONLINE.COM Furniture E-MAIL：[email protected] B (10.2A19-20)漳州玉致家具有限公司 ZHANGZHOU YUZHI FURNITURE CO., LTD. *(10.2A01-03)厦门金华南进出口有限公司 福建省漳州市金峰工业开发区北斗工业园 区 XIAMEN GOLDEN HUANAN IMP. & EXP. CO., LTD. (邮政编码：363000) 厦门湖里大道保税市场大厦第8层G单元 BEIDOU INDUSTRIAL PARK, JINFENG INDUSTRIAL DEVELOPMENT (邮政编码：361006) ZONE, ZHANGZHOU, FUJIAN, CHINA UNIT G, 8/F., XIAMEN BONDED GOODS MARKET BUILDING, HULI TEL：86-596-2527908 FAX：86-596-2600567 AV., XIAMEN E-MAIL：[email protected] TEL：86-592-5620989 FAX：86-592-5620969 家具 URL：WWW.GOLDEN-SOUTH.COM *(10.2A21-22)北京工艺艺嘉贸易有限责任公 E-MAIL：[email protected] 司 BEIJING ART RESOURCES CO., LTD. (10.2A04-06)山东汇洋经贸有限公司 北京市建外大街10号 SHANDONG HUIYANG INDUSTRY CO., LTD. (邮政编码：100022) 济南市趵突泉北路6号402室 NO.10, JIANGUOMENWAI AV., BEIJING, CHINA (邮政编码：250011) TEL：86-10-65682324 FAX：86-10-65681284 ROOM 402, NO.6, BAOTUQUAN NORTH ROAD, JINAN, CHINA URL：BJARTSCRAFTS.COM TEL：86-531-86092958 FAX：86-531-86092955 E-MAIL：[email protected] URL：WWW.SHANDONGHUIYANG.CN E-MAIL：[email protected] (10.2A23-24, 10.2B01-02)宁波中基人和国 际贸易有限公司 B Area (10.2A07-12)广州交易会进出口有限公司 NINGBO CHINA-BASE LANDHAU FOREIGN TRADE CO., CANTON FAIR IMP. & EXP. CO., LTD. LTD. 广州市海珠区凤浦中路679号广交易大厦七楼 宁波市天童南路666号中基大厦 (邮政编码：510335) (邮政编码：315199) 7/F., CANTON FAIR BUILDING, NO.679, FENGPU MID. RD., HAIZHU CHINA-BASE PLAZA, NO.666, TIANTONG SOUTH ROAD, NINGBO, Furniture DISTRICT, GUANGZHOU, CHINA CHINA TEL：86-20-89268303 FAX：86-20-86666927 TEL：86-574-87425505 FAX：86-574-87425564 URL：WWW.CANTONFAIRCO.COM URL：WWW.CBNB.COM.CN E-MAIL：[email protected] E-MAIL：[email protected] *(10.2A13-16)福建德艺集团股份有限公司 (10.2B03-04)北京工艺艺嘉贸易有限责任公 FUJIAN PROFIT GROUP CORPORATION 司 中国福建省福州市五四路158号环球广场18层1-5单 BEIJING ART RESOURCES CO., LTD.
    [Show full text]