Accelerators
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

NRP-3 the Effect of Beryllium Interaction with Fast Neutrons on the Reactivity of Etrr-2 Research Reactor
Seventh Conference of Nuclear Sciences & Applications 6-10 February 2000, Cairo, Egypt NRP-3 The Effect Of Beryllium Interaction With Fast Neutrons On the Reactivity Of Etrr-2 Research Reactor Moustafa Aziz and A.M. EL Messiry National Center for Nuclear Safety Atomic Energy Autho , Cairo , Egypt ABSTRACT The effect of beryllium interactions with fast neutrons is studied for Etrr_2 research reactors. Isotope build up inside beryllium blocks is calculated under different irradiation times. A new model for the Etrr_2 research reactor is designed using MCNP code to calculate the reactivity and flux change of the reactor due to beryllium poison. Key words: Research Reactors , Neutron Flux , Beryllium Blocks, Fast Neutrons and Reactivity INTRODUCTION Beryllium irradiated by fast neutrons with energies in the range 0.7-20 Mev undergoes (n,a) and (n,2n) reactions resulting in subsequent formation of the isotopes lithium (Li-6), tritium (H-3) and helium (He-3 and He-4 ). Beryllium interacts with fast neutrons to produce 6He that decay 6 6 ( T!/2 =0.8 s) to produce Li . Li interacts with neutron to produce tritium which suffer /? (T1/2 = 12.35 year) decay and converts to 3He which finally interact with neutron to produce tritium. These processes some times defined as Beryllium poison. Negative effect of this process are met whenever beryllium is used in a thermal reactor as a reflector or moderator . Because of their large thermal neutron absorption cross sections , the buildup of He-3 and Li-6 concentrations ,initiated by the Be(n,a) reaction , results in large negative reactivities which alter the reactivity , flux and power distributions. -

Hadron Collider Physics
KEK-PH Lectures and Workshops Hadron Collider Physics Zhen Liu University of Maryland 08/05/2020 Part I: Basics Part II: Advanced Topics Focus Collider Physics is a vast topic, one of the most systematically explored areas in particle physics, concerning many observational aspects in the microscopic world • Focus on important hadron collider concepts and representative examples • Details can be studied later when encounter References: Focus on basic pictures Barger & Philips, Collider Physics Pros: help build intuition Tao Han, TASI lecture, hep-ph/0508097 Tilman Plehn, TASI lecture, 0910.4182 Pros: easy to understand Maxim Perelstein, TASI lecture, 1002.0274 Cons: devils in the details Particle Data Group (PDG) and lots of good lectures (with details) from CTEQ summer schools Zhen Liu Hadron Collider Physics (lecture) KEK 2020 2 Part I: Basics The Large Hadron Collider Lyndon R Evans DOI:10.1098/rsta.2011.0453 Path to discovery 1995 1969 1974 1969 1979 1969 1800-1900 1977 2012 2000 1975 1983 1983 1937 1962 Electric field to accelerate 1897 1956 charged particles Synchrotron radiation 4 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 4 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 5 Why study (hadron) colliders (now)? • Leading tool in probing microscopic structure of nature • history of discovery • Currently running LHC • Great path forward • Precision QFT including strong dynamics and weakly coupled theories • Application to other physics probes • Set-up the basic knowledge to build other subfield of elementary particle physics Zhen Liu Hadron Collider Physics (lecture) KEK 2020 6 Basics: Experiment & Theory Zhen Liu Hadron Collider Physics (lecture) KEK 2020 7 Basics: How to make measurements? Zhen Liu Hadron Collider Physics (lecture) KEK 2020 8 Part I: Basics Basic Parameters Basics: Smashing Protons & Quick Estimates Proton Size ( ) Proton-Proton cross section ( ) Particle Physicists use the unit “Barn”2 1 = 100 The American idiom "couldn't hit the broad side of a barn" refers to someone whose aim is very bad. -

HEPAP Looks Into the Future
Volume 20 Friday, August 29, 1997 Number 17 f INSIDE HEPAP Looks into 2 HEPAP: Voice of the Community the Future 5 Profiles in HEPAP subpanel meets at Fermilab to chart the future of Particle Physics: high-energy physics in the U.S. Dave McGinnis by Donald Sena and Sharon Butler, Office of Public Affairs 6 Barns of Fermilab Charged with recommending how best to In a letter to HEPAP, Martha Krebs, position the U.S. particle physics community Director of the U.S. Department of Energy’s for new facilities beyond CERN’s Large Office of Energy Research, directed the Hadron Collider, a subpanel of the High- subpanel to “recommend a scenario for an Energy Physics Advisory Panel met at Fermilab optimal and balanced U.S. high-energy physics August 14-16 to hear presentations on such program over the next decade,” with “new topics as the research agenda for Fermilab’s facilities to address physics opportunities Run II, the complicated upgrades to the CDF beyond the LHC.” She asked the subpanel and DZero detectors and research on future to consider a future course in light of three accelerators. continued on page 3 Photo by Reidar Hahn Dixon Bogert, deputy project manager for the Main Injector, leads a tour for HEPAP subpanel members and DOE officials. HEPAP: Voice of the Community by Donald Sena and Sharon Butler, Office of Public Affairs The High-Energy Physics Advisory In 1983, for example, a HEPAP According to Fermilab physicist Cathy Panel traces its history to the 1960s, subpanel recommended terminating Newman-Holmes, outgoing member of when -

Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems
Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1222 Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems DANIEL PELIKAN ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6214 ISBN 978-91-554-9153-6 UPPSALA urn:nbn:se:uu:diva-242491 2015 Dissertation presented at Uppsala University to be publicly examined in Polhemssalen, Ångströmlaboratoriet, Lägerhyddsvägen 1, Uppsala, Friday, 20 March 2015 at 10:00 for the degree of Doctor of Philosophy. The examination will be conducted in English. Faculty examiner: Prof. Dr. Fabrizio Palla (Istituto Nazionale di Fisica Nucleare (INFN) Pisa). Abstract Pelikan, D. 2015. Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems. Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1222. 119 pp. Uppsala: Acta Universitatis Upsaliensis. ISBN 978-91-554-9153-6. The discovery of a charged Higgs boson (H±) would be a clear indication for physics beyond the Standard Model. This thesis describes searches for charged Higgs bosons with the ATLAS experiment at CERN’s Large Hadron Collider (LHC). The first data collected during the LHC Run 1 is analysed, searching for a light charged Higgs boson (mH±<mtop), which decays predominantly into a tau-lepton and a neutrino. Different final states with one or two leptons (electrons or muons), as well as leptonically or hadronically decaying taus, are studied, and exclusion limits are set. The background arising from misidentified non-prompt electrons and muons was estimated from data. This so-called "Matrix Method'' exploits the difference in the lepton identification between real, prompt, and misidentified or non-prompt electrons and muons. -
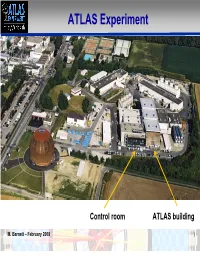
ATLAS Experiment
ATLAS Experiment Control room ATLAS building M. Barnett – February 2008 1 Final piece of ATLAS lowered last Friday (the second small muon wheel) M. Barnett – February 2008 2 M. Barnett – February 2008 3 Still to be done Connecting: Cables, Fibers, Cryogenics M. Barnett – February 2008 4 Celebrations M. Barnett – February 2008 5 News Coverage News media are flooding CERN well in advance of startup "Particle physics is the unbelievable in pursuit of the unimaginable. To pinpoint the smallest fragments of the universe you have to build the biggest machine in the world. To recreate the first millionths of a second of creation you have to focus energy on an awesome scale." The Guardian M. Barnett – February 2008 6 Three full pages in New York Times M. Barnett – February 2008 7 New York Times M. Barnett – February 2008 8 National Geographic Magazine M. Barnett – February 2008 9 National Geographic Magazine M. Barnett – February 2008 10 National Geographic Magazine M. Barnett – February 2008 11 M. Barnett – February 2008 12 M. Barnett – February 2008 13 M. Barnett – February 2008 14 M. Barnett – February 2008 15 M. Barnett – February 2008 16 M. Barnett – February 2008 17 M. Barnett – February 2008 18 M. Barnett – February 2008 19 M. Barnett – February 2008 20 M. Barnett – February 2008 21 M. Barnett – February 2008 22 And on television (shortened version) M. Barnett – February 2008 23 An ATLAS expert explains the Higgs evidence to a layperson. M. Barnett – February 2008 24 US-LHC Student Journalism Program April 2-7, 2008 (overlapping Open Days) Six teams of high school students (3 students/1 teacher) are going to CERN to report on the LHC startup. -

How and Why to Go Beyond the Discovery of the Higgs Boson
How and Why to go Beyond the Discovery of the Higgs Boson John Alison University of Chicago http://hep.uchicago.edu/~johnda/ComptonLectures.html Lecture Outline April 1st: Newton’s dream & 20th Century Revolution April 8th: Mission Barely Possible: QM + SR April 15th: The Standard Model April 22nd: Importance of the Higgs April 29th: Guest Lecture May 6th: The Cannon and the Camera May 13th: The Discovery of the Higgs Boson May 20th: Problems with the Standard Model May 27th: Memorial Day: No Lecture June 3rd: Going beyond the Higgs: What comes next ? 2 Reminder: The Standard Model Description fundamental constituents of Universe and their interactions Triumph of the 20th century Quantum Field Theory: Combines principles of Q.M. & Relativity Constituents (Matter Particles) Spin = 1/2 Leptons: Quarks: νe νµ ντ u c t ( e ) ( µ) ( τ ) ( d ) ( s ) (b ) Interactions Dictated by principles of symmetry Spin = 1 QFT ⇒ Particle associated w/each interaction (Force Carriers) γ W Z g Consistent theory of electromagnetic, weak and strong forces ... ... provided massless Matter and Force Carriers Serious problem: matter and W, Z carriers have Mass ! 3 Last Time: The Higgs Feild New field (Higgs Field) added to the theory Allows massive particles while preserve mathematical consistency Works using trick: “Spontaneously Symmetry Breaking” Zero Field value Symmetric in Potential Energy not minimum Field value of Higgs Field Ground State 0 Higgs Field Value Ground state (vacuum of Universe) filled will Higgs field Leads to particle masses: Energy cost to displace Higgs Field / E=mc 2 Additional particle predicted by the theory. Higgs boson: H Spin = 0 4 Last Time: The Higgs Boson What do we know about the Higgs Particle: A Lot Higgs is excitations of v-condensate ⇒ Couples to matter / W/Z just like v X matter: e µ τ / quarks W/Z h h ~ (mass of matter) ~ (mass of W or Z) matter W/Z Spin: 0 1/2 1 3/2 2 Only thing we don’t (didn’t!) know is the value of mH 5 History of Prediction and Discovery Late 60s: Standard Model takes modern form. -

Nuclear Criticality Safety Engineer Training Module 1 1
Nuclear Criticality Safety Engineer Training Module 1 1 Introductory Nuclear Criticality Physics LESSON OBJECTIVES 1) to introduce some background concepts to engineers and scientists who do not have an educational background in nuclear engineering, including the basic ideas of moles, atom densities, cross sections and nuclear energy release; 2) to discuss the concepts and mechanics of nuclear fission and the definitions of fissile and fissionable nuclides. NUCLEAR CRITICALITY SAFETY The American National Standard for Nuclear Criticality Safety in Operations with Fissionable Materials Outside Reactors, ANSI/ANS-8.1 includes the following definition: Nuclear Criticality Safety: Protection against the consequences of an inadvertent nuclear chain reaction, preferably by prevention of the reaction. Note the words: nuclear - related to the atomic nucleus; criticality - can it be controlled, will it run by itself; safety - protection of life and property. DEFINITIONS AND NUMBERS What is energy? Energy is the ability to do work. What is nuclear energy? Energy produced by a nuclear reaction. What is work? Work is force times distance. 1 Developed for the U. S. Department of Energy Nuclear Criticality Safety Program by T. G. Williamson, Ph.D., Westinghouse Safety Management Solutions, Inc., in conjunction with the DOE Criticality Safety Support Group. NCSET Module 1 Introductory Nuclear Criticality Physics 1 of 18 Push a car (force) along a road (distance) and the car has energy of motion, or kinetic energy. Climb (force) a flight of steps (distance) and you have energy of position relative to the first step, or potential energy. Jump down the stairs or out of a window and the potential energy is changed to kinetic energy as you fall. -

Long-Range Beam–Beam Effects in the Tevatron* V
Published by CERN in the Proceedings of the ICFA Mini-Workshop on Beam–Beam Effects in Hadron Colliders, CERN, Geneva, Switzerland, 18–22 March 2013, edited by W. Herr and G. Papotti, CERN–2014–004 (CERN, Geneva, 2014) LONG-RANGE BEAM–BEAM EFFECTS IN THE TEVATRON* V. Shiltsev#, A.Valishev, FNAL, Batavia, IL, USA Abstract Long-range beam–beam effects occurred in the Tevatron at all stages (injection, ramp, squeeze, and collisions) and affected both proton and antiproton beams. They resulted in beam losses and emittance blow-ups, which occurred in remarkable bunch-to-bunch dependent patterns. On the way to record-high luminosities of the collider, many issues related to the long-range beam– beam interactions have been addressed. Below we present a short overview of the long-range beam–beam effects in the Tevatron. (For a detailed discussion on the beam– beam effects in the Tevatron please see reviews in Refs. [1–3] and references therein). HELICAL ORBITS IN TEVAT R O N Beam–beam interactions in the Tevatron differ between the injection and collision stages. The helical orbits were introduced to provide sufficient separation between the proton and antiproton beams in order to reduce Figure 2: The pattern of the Tevatron helical orbits at the detrimental beam–beam effects, e.g. tune shifts, coupling, collision stage. and high-order resonance driving terms. In 36 × 36 bunch Initially, there were six separator groups (three operation, each bunch experienced 72 long-range horizontal and three vertical) in the arcs between the two interactions per revolution at injection, but at collision main interaction points, B0 (CDF) and D0. -

U.S. and CERN Sign LHC Agreement
Volume 21 Friday, January 9, 1998 Number 1 f INSIDE U.S. and CERN 4 Near-Beam Physics Sign LHC Agreement 6 Dear Mr. Ellis 8 Profiles in Particle Physics: American scientists, Treaty Room, CERN Director- Chuck Marofske including many from General Chris Llewellyn Smith Fermilab, will help posed a question. 9 Electrical Accident “By ‘Large Event,’” he build the Large 10 Banners wondered, “do you think Hadron Collider they mean the Higgs?” in Europe. Whether or not the new Large Hadron By Judy Jackson, Office Collider to be built at of Public Affairs CERN, the European Laboratory for Particle As they cleared Physics in Geneva, security at the entrance to ultimately identifies the Old Executive Office an event containing Building across the street the putative mass- from the White House, guests conferring particle CERN Photo and dignitaries bound for the called the Higgs December 8 signing ceremony Simulation of a boson, the for the Large Hadron Collider Higgs boson decay. ceremony donned mandatory plastic ID tags confirming stamped with the words “Large U.S. participation Event.” Looking around at the tags in the project was adorning the veritable Who’s Who of definitely a Large Event. U.S. particle physics and Washington science hands filling the ornate Indian continued on page 2 NSF Director Neal Lane, Secretary of Energy Federico Peña, CERN Council President Luciano Maiani and CERN Director-General Chris Llewellyn Smith immediately after signing the LHC agreement in the Indian Treaty Room. DOE Photo be delivered to CERN, will total $531 million over eight years, with $450 million coming from the Department of Energy and the remaining $81 million from NSF. -

Signal to Background
signal to background Origin of the (classified) barn; meet the shoemobile; creative ways to use symmetry; birds at Fermilab; scientists playing Indiana Jones; battle of the boxes; Late Show with Lederman; letters. One big step for safety It looks like a simple silver trailer, but it’s more like a shoe store on wheels. Mike Sitarz pulls his metal trailer, better known among Fermilab employees as the “shoemobile,” behind the Technical Division industrial buildings at 8 a.m. every Tuesday. He stays until 4 p.m., fitting employees with safety shoes required for their jobs. Sitarz’s store, Knippen Shoes, located in Wheaton, Illinois, Photo: Reidar Hahn, Fermilab is contracted by Fermilab’s Environmental Safety & Health Hitting the broad decided “Manley” was too long, Section to make weekly visits. side of a (classified) and then, as the authors put it Inside the carpeted trailer, barn in the Physics Today article to: stacks of cardboard boxes line In the luminosity lexicon, a “‘John’ was considered, but the walls and fitting chairs picobarn is one trillionth (10-12) was discarded because of the await customers. Sitarz, who’s of a barn, and a femtobarn is use of the term for purposes been making the trip to Fermi- one quadrillionth (10-15) of a other than as the name of a lab for 11 years, carries about barn… but what’s a barn? The person. The rural background of 350 pairs of shoes, ranging distinctive and amusing term one of the authors then led to from Skechers to Red Wings. originated with two Purdue the bridging of the gap between Employees required to wear University physicists working the ‘John’ and the ‘barn.’ This special work shoes receive on the Manhattan Project in immediately seemed good, and a footwear request signed by 1942–and it was classified further it was pointed out that a their supervisor detailing the information by the US govern- cross section of 10-24 cm2 for safety features that are needed. -

Analysis of Wwy Production with the ATLAS Experiment
Dissertation submitted to the Combined Faculties of the Natural Sciences and Mathematics of the Ruperto-Carola-University of Heidelberg, Germany for the degree of Doctor of Natural Sciences Put forward by Julia Isabell Djuvsland born in Heidelberg Oral examination on July 28th, 2016 Analysis of W W γ production with the ATLAS experiment Referees: Prof. Dr. Hans-Christian Schultz-Coulon Prof. Dr. Stephanie Hansmann-Menzemer Abstract In this thesis, triboson final states containing two W bosons and a photon are studied using proton-proton collisions.p The data set was recorded with the ATLAS detector at a centre- of-mass energy of s = 8 TeV and corresponds to an integrated luminosity of 20.3 fb−1. The fiducial cross-section of the process W W γ ! eνµνγ is measured for the first time in hadron eµγ collisions and corresponds to σfid. = (1:89 ± 0:93(stat.) ± 0:41(syst.) ± 0:05(lumi.)) fb. It is in good agreement with the Standard Model prediction at next-to-leading order in the strong coupling constant. As no deviation from the Standard Model expectation is observed, frequentist limits at 95 % confidence level are computed to exclude contributions from anomalous quartic gauge couplings. This analysis is sensitive to fourteen coupling parameters of mass dimension eight and the limits are derived for all parameters with and without unitarisation. Zusammenfassung In der vorliegenden Arbeit wird die simultane Produktion eines Photons und zweier W - Bosonen analysiert. Die studiertenp Protonkollisionen wurden mit dem ATLAS-Detektor bei einer Schwerpunktsenergie von s = 8 TeV aufgezeichnet und entsprechen einer inte- grierten Luminosität von 20.3 fb−1. -

The Run II of the Tevatron
FEATURES ... The Run 11 ofthe Tevatron Jean-Fran~ois Grivaz Laboratoire de I'Accelerateur Lineaire, Orsay igh energy physics is the denomination commonly used to H designate the physics ofelementary particles, the branch of physics which deals with the building blocks ofmatter (quarks and leptons, as it presently seems) and their interactions. The reason for this denomination is that high energy beams are nec essary to probe short distances, which is why higher and higher energyparticle accelerators have been and continue to bebuilt. As oftoday, the particle accelerator providingthe highest energies is the Tevatron, a proton-antiproton collider located at Fermilab [1] (the Fermi National Accelerator Laboratory) near Chicago, Illinois (Fig. 1). Bunches ofprotons and antiprotons circulate in opposite directions in a 6.28 km long ring, and collide head on at specific locations where two large and complex detectors, named CDF [2] and DO [3], register the outcome oftheir interactions. The Tevatron collider operated from 1992 to 1996, at a centre-of I A Fig. 1: An aerial view of the Fermilab site.The main mass energyl) (twice the beam energy) of 1.8 TeV, delivering to I components ofthe accelerator system are highlighted: in yellow, each experimentanintegratedluminosity(2) of120 pb-I • Themain , the Tevatron, a 2 TeV proton-antiproton collider; in red the initial achievement ofthis period, known as Run I, was the discovery of I injection system; in blue the newly constructed main injector and the long sought top quark [4], with a mass of174 Gev, in 1995. i recycler. The locations of the (OF and DO detectors are also With the discovery ofthe top quark, the only missing piece in I indicated.