DOCSLIB.ORG

Hadron Collider Physics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hadron Collider Physics KEK-PH Lectures and Workshops Hadron Collider Physics Zhen Liu University of Maryland 08/05/2020 Part I: Basics Part II: Advanced Topics Focus Collider Physics is a vast topic, one of the most systematically explored areas in particle physics, concerning many observational aspects in the microscopic world • Focus on important hadron collider concepts and representative examples • Details can be studied later when encounter References: Focus on basic pictures Barger & Philips, Collider Physics Pros: help build intuition Tao Han, TASI lecture, hep-ph/0508097 Tilman Plehn, TASI lecture, 0910.4182 Pros: easy to understand Maxim Perelstein, TASI lecture, 1002.0274 Cons: devils in the details Particle Data Group (PDG) and lots of good lectures (with details) from CTEQ summer schools Zhen Liu Hadron Collider Physics (lecture) KEK 2020 2 Part I: Basics The Large Hadron Collider Lyndon R Evans DOI:10.1098/rsta.2011.0453 Path to discovery 1995 1969 1974 1969 1979 1969 1800-1900 1977 2012 2000 1975 1983 1983 1937 1962 Electric field to accelerate 1897 1956 charged particles Synchrotron radiation 4 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 4 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 5 Why study (hadron) colliders (now)? • Leading tool in probing microscopic structure of nature • history of discovery • Currently running LHC • Great path forward • Precision QFT including strong dynamics and weakly coupled theories • Application to other physics probes • Set-up the basic knowledge to build other subfield of elementary particle physics Zhen Liu Hadron Collider Physics (lecture) KEK 2020 6 Basics: Experiment & Theory Zhen Liu Hadron Collider Physics (lecture) KEK 2020 7 Basics: How to make measurements? Zhen Liu Hadron Collider Physics (lecture) KEK 2020 8 Part I: Basics Basic Parameters Basics: Smashing Protons & Quick Estimates Proton Size ( ) Proton-Proton cross section ( ) Particle Physicists use the unit “Barn”2 1 = 100 The American idiom "couldn't hit the broad side of a barn" refers to someone whose aim is very bad. Enrico Fermi said the neutrons2 hits nuclear reactor nucleus as easy as hitting the broad side of a barn. Proton-Proton cross section is then 10 , actually ~20 mb for hard scattering and 100 mb for total scattering. In natural units ( ~)200 1 −1 Zhen Liu Hadron Collider Physics (lecture) Λ KEK 2020 ≃ 10 Basics: Smashing Protons & Quick Estimates Particle Physicists use the unit “Barn” Beam of colliding 1 = 100 = 10 particles are the Proton-Proton cross section2 is ~100−28 mb2 for microscope for us. total scattering. LHC is 3 Beam power is called (# / /sec) ILC 250 GeV− 12 Instantaneous Luminosity, typical value2 is FCC-ee/CEPC 5 −1 10 = 10 FCC-hh 30 −1 A typical year34 is− 210 sec−1 , for 10 years−1 , −1 −1 accumulating Integrated7 Luminosity, = 10 = 1 9 −1 −1 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 11 Basics: typical cross sections Amongst the collisions, most are not of too much interests to us (either soft scattering, corresponding to known low energy physics, or too massy to interpret), only a small fraction of the collisions are our primary targets. At 14 TeV LHC: How did we calculate the rate Inclusive: 100 and develop a strategy to Dijets (pT> 50 GeV):discover 20 Higgs at the LHC? W: 200 Z: 50 Top quark pair: 800 WW: 100 H: 50 (× =150 ) : 10 −1 3 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 12 Part I: Basics Basic Parameters Basic Cross Sections & Representation At hadron colliders, we are smashing protons. Cross Sections Protons are composite. We are colliding the constituents. ( ) = × × → → Center of 1 Mass 4 Energy × Σ − Σ 4 .. 2 0 � 3 2 =1 2 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 14 Partonic Cross Sections (Hard Scattering) “Parton”—proton constituents� ( ) = × × �→ � → Partonic 1 4 Center of × Σ − Σ 4 Mass .. 2 0 2 � 3 Energy =1 2 < ̂ Zhen Liu � Hadron Collider Physics (lecture) KEK 2020 15 Hadron Collider Representation lab frame center of mass frame but can be translated via Lorentz Boost in the Z-direction = ( , 0≠,0, ), = ( , 0,0, ) Collider (Beam) center of mass energy = , e.g., LHC is 14 TeV with 7 TeV on each beam, ILC 250 is 250 GeV S with 125 GeV on each1 beam. 2 2 Hadron colliders can only use part of the total2 energy as it effectively colliding− partons = ( , 0,0, ), = ( , 0,0, ) Viewing parton 1 and 2 as a system, its Invariant mass (c.o.m.1energy): 1 1 2 2 2 = + = = − Velocity ( ) & Rapidity ( ) in lab frame: 2 1 2 1 2 1 2 =̂ ( )/( + ), Y2= log( / ) 1 1 − 2 1 2 2 1 2 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 16 Rapidity Rapidity: 1 + ln 2 General 4-momenta: ≡ = cosh , sin , − cos , sinh with + , + 2 2 2 2 Rapidity ≡ is additive for boost≡ along z-direction (reference rapidity of ) = 0 ′ Very useful Rapidity difference invariant under boost 0in z-direction = − properties for hadron colliders, Hence allow trivial differential′ translation′ (Jacobian of 1) − − which needs boost = in the z-direction ′ Zhen Liu Hadron Collider Physics (lecture) KEK 2020 17 Rapidity & Pseudo Rapidity Rapidity: Pseudo-Rapidity: 1 + 1 + ln ln 2 2 ⃗ Rapidity is additive≡ for boost along z- For massless particles≡ direction (reference rapidity− of ) =⃗ − = 0 inherit all the properties. ′ Rapidity difference invariant0 under In the limit of boost in z-direction − = ≫ ′ ′ all the properties approximately hold Hence allow trivial differential ≈ translation (Jacobian− of− 1) = No above properties for massive particles ′ Zhen Liu Hadron Collider Physics (lecture) KEK 2020 18 Pseudo Rapidity representing Geometry Pseudo-Rapidity: 1 + 1 1 + cos ln = ln = ln cot 2 2 1 cos 2 ⃗ ≡ Recall that two-body phase ⃗ − − space = cos Compared 1to cos , is 2 8 preferred phase space measure, e.g., a spinless particle decay is “flat” in cos not Approximately linear (in both cos and ) in the central region (|cos | < 1) “zoom in” for forward region (|cos |~1) Zhen Liu Hadron Collider Physics (lecture) KEK 2020 19 Pseudo Rapidity representing Geometry Pseudo-Rapidity: 1 + 1 1 + cos ln = ln = ln cot 2 2 1 cos 2 ⃗ ≡ ⃗ − − Experimentally, the hadron collider geometry are expressed in pseudo rapidity Zhen Liu Hadron Collider Physics (lecture) KEK 2020 20 Pseudo Rapidity representing Geometry Pseudo-Rapidity: 1 + 1 1 + cos ln = ln = ln cot 2 2 1 cos 2 ⃗ ≡ ⃗ − − Experimentally, the hadron collider geometry are expressed in pseudo rapidity Typical high mass/energy events (central: Barrel & EndCap): | | < 3 Forward (lots of QCD background) > 3 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 21 Part I: Basics Basic Parameters Basic Cross Sections & Representation Parton Distribution Functions Factorization Short distance physics (large momentum transfer) should not depend on long distances physics. = , → ∫ 12Σ 1 2 �→ ̂ Used as working assumption = QCD factorization proven for certain processes QED factorization proven ̂ 12 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 23 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 24 Parton Distribution Functions (PDFs) Partons are weakly bound (when probed) constituents of hadrons. Feynman; Bjorken, Paschos-1969 Collinear PDFs ( , ) are the simplest functions describing the nonperturbative hadron structure. (In the simplest interpretation) ( , ) is the probability to find a parton a carrying momentum of the initial hadron with momentum , with a probing scale of . Zhen Liu Hadron Collider Physics (lecture) KEK 2020 25 Parton Distribution Functions (PDFs) PDFs ( , ) are universal, independent of the hard- scattering process. The structure of the hadron drastically as a function of the probing scale Q, obeying Dokshitzer-Gribov-Lipatov- Altarelli-Parisi (DGLAP) equations ( , ) = , ( , ) 1 / , , , , ,… � � � � / are the probabilities= for colinear splitting. Zhen Liu Hadron Collider Physics (lecture) → KEK 2020 26 Hard: large momentum transfer Soft: small momentum transfer Zhen Liu Hadron Collider Physics (lecture) KEK 2020 27 Reasonable (boundary conditions) for PDFs Momentum sum-rule (conservation) , = 1 1 , , , , ,… � �0 Valence sum rule, =e.g., � for � protons (uud) [ , , ] = 2 1 � � [ , − , ] = 1 01 � � [ , − , ] = 0 Sea quark 0 1 � − ̅ Zhen Liu Hadron Collider0 Physics (lecture) KEK 2020 28 Recall that Up and Down are valence quarks, their PDF have a peak at x~1/3, valence quark effect at low 2 PDF rise rapidly at low x due to perturbative evolution (splitting) Zhen Liu Hadron Collider Physics (lecture) KEK 2020 29 As Q increases, high x partons lose momentum through QCD radiation Up Quark PDF evolution (splitting) Zhen Liu Hadron Collider Physics (lecture) KEK 2020 30 As Q increases, high x partons lose momentum through QCD radiation (splitting), gluon PDF Gluon PDF evolution dominants and sea quark Up anti-quark PDF evolution PDF follows Zhen Liu Hadron Collider Physics (lecture) KEK 2020 31 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 32 PDF (as a function of ) = ̂ , = → 1 2 , 1 2 ()→ ∫ 1 Σ � ̂ ∫ Useful̂ tô Σ quickly1 estimate1 2 high2 energy�→ ̂ physics processes PDF drops as a high power (5-6 power) as a function of the enter of mass energy ̂ Zhen Liu Hadron Collider Physics (lecture) KEK 2020 33 “Inverse Process” of fragmentation and hadronization Fig. Credit: Zhen Liu Hadron Collider Physics (lecture) KEK 2020 Eric M. Metodiev 34 Part I: Basics Basic Parameters Basic Cross Sections & Representation Parton Distribution Functions
Load more

Recommended publications
  • NRP-3 the Effect of Beryllium Interaction with Fast Neutrons on the Reactivity of Etrr-2 Research Reactor
    Seventh Conference of Nuclear Sciences & Applications 6-10 February 2000, Cairo, Egypt NRP-3 The Effect Of Beryllium Interaction With Fast Neutrons On the Reactivity Of Etrr-2 Research Reactor Moustafa Aziz and A.M. EL Messiry National Center for Nuclear Safety Atomic Energy Autho , Cairo , Egypt ABSTRACT The effect of beryllium interactions with fast neutrons is studied for Etrr_2 research reactors. Isotope build up inside beryllium blocks is calculated under different irradiation times. A new model for the Etrr_2 research reactor is designed using MCNP code to calculate the reactivity and flux change of the reactor due to beryllium poison. Key words: Research Reactors , Neutron Flux , Beryllium Blocks, Fast Neutrons and Reactivity INTRODUCTION Beryllium irradiated by fast neutrons with energies in the range 0.7-20 Mev undergoes (n,a) and (n,2n) reactions resulting in subsequent formation of the isotopes lithium (Li-6), tritium (H-3) and helium (He-3 and He-4 ). Beryllium interacts with fast neutrons to produce 6He that decay 6 6 ( T!/2 =0.8 s) to produce Li . Li interacts with neutron to produce tritium which suffer /? (T1/2 = 12.35 year) decay and converts to 3He which finally interact with neutron to produce tritium. These processes some times defined as Beryllium poison. Negative effect of this process are met whenever beryllium is used in a thermal reactor as a reflector or moderator . Because of their large thermal neutron absorption cross sections , the buildup of He-3 and Li-6 concentrations ,initiated by the Be(n,a) reaction , results in large negative reactivities which alter the reactivity , flux and power distributions.
    [Show full text]
  • Diffractive Dissociation of Alpha Particles As a Test of Isophobic Short-Range Correlations Inside Nuclei ∗ Jennifer Rittenhouse West A, , Stanley J
    Physics Letters B 805 (2020) 135423 Contents lists available at ScienceDirect Physics Letters B www.elsevier.com/locate/physletb Diffractive dissociation of alpha particles as a test of isophobic short-range correlations inside nuclei ∗ Jennifer Rittenhouse West a, , Stanley J. Brodsky a, Guy F. de Téramond b, Iván Schmidt c a SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94309, USA b Laboratorio de Física Teórica y Computacional, Universidad de Costa Rica, 11501 San José, Costa Rica c Departamento de Física y Centro Científico Tecnológico de Valparáiso-CCTVal, Universidad Técnica Federico Santa María, Casilla 110-V, Valparaíso, Chile a r t i c l e i n f o a b s t r a c t Article history: The CLAS collaboration at Jefferson Laboratory has compared nuclear parton distributions for a range Received 15 January 2020 of nuclear targets and found that the EMC effect measured in deep inelastic lepton-nucleus scattering Received in revised form 9 April 2020 has a strongly “isophobic” nature. This surprising observation suggests short-range correlations between Accepted 9 April 2020 neighboring n and p nucleons in nuclear wavefunctions that are much stronger compared to p − p or n − Available online 14 April 2020 n correlations. In this paper we propose a definitive experimental test of the nucleon-nucleon explanation Editor: W. Haxton of the isophobic nature of the EMC effect: the diffractive dissociation on a nuclear target A of high energy 4 He nuclei to pairs of nucleons n and p with high relative transverse momentum, α + A → n + p + A + X. The comparison of n − p events with p − p and n − n events directly tests the postulated breaking of isospin symmetry.
    [Show full text]
  • Novel Features of Nuclear Chromodynamics
    SLAC-PUB-16868 Novel Features of Nuclear Chromodynamics Stanley J. Brodsky1 SLAC National Accelerator Laboratory Stanford University, Stanford, CA, 94309 the date of receipt and acceptance should be inserted later Abstract. I review a number of QCD topics where the nuclear environment provides new insights into fundamental aspects of the strong interactions. Quarks, gluons, and QCD in nuclear reactions PACS. 2 4.85.+p Pn Pn 1 Introduction where i xi = 1; i k i = 0: It is convenient to choose the \light-cone" gauge ?A+ = 0 so that the gluons only One of the most challenging problems in QCD is to un- have physical polarization Sz = 1 and no ghosts appear. H ± derstand nuclei in terms of their fundamental quark and Remarkably, the n (xi; k i; λi) LFWFs are independent ? gluon degrees of freedom. Even the deuteron has exotic of the hadron's momentum P +; P . There is no Lorentz ? features such as its \hidden" color degrees of freedom. In contraction of LFWFs [3,4]. The structure functions mea- this article I will review some new perspectives for nuclear sured in deep inelastic scattering on a fixed target in the physics, such as nuclear form factors and the nuclear force rest frame is the same structure function measured in an at short distances, which are consequences of fundamen- electron-ion coliider. In fact, the LF formalism is Poincare' tal features of QCD [1]. Conversely, the nuclear environ- invariant { all formulae are independent of the observer's ment can bring new insights of hadron physics, such as Lorentz frame.
    [Show full text]
  • Arxiv:1810.00233V1 [Hep-Ph] 29 Sep 2018 233.2 Mev and 455.6 Mev Respectively) Including O(Α) More Complicated Inclusive J/Ψ → Xhγ [45]
    Scouring meson decays for true muonium Yao Ji∗ Institut f¨urTheoretische Physik, Universit¨atRegensburg, Regensburg 93040, Germany Henry Lamm† Department of Physics, University of Maryland, College Park, MD 20742 (Dated: October 2, 2018) Rare meson decay experiments promise to measure branching ratios as small as 10−13. This presents an opportunity to discover the µ+µ− bound state true muonium. We consider a set of possible channels, all with branching ratios above ∼ 10−11. For the electromagnetic decays η/η0 → + − 2 0 (µ µ )γ, theoretical and phenomenological form factors Fη/η0γγ∗ (Q ) allow predictions of BR(η → (µ+µ−)γ) ∼ 4.8 × 10−10 and BR(η0 → (µ+µ−)γ) ∼ 3.7 × 10−11 at the 5% level. Discussion of experimental prospects and potential backgrounds are made. Within the Standard Model, only the Higgs interaction breaks lepton universality, but the discovery of neutrino TABLE I. Meson decay branching ratios involving photons considered in this work. The first two are electromagnetic masses implies that at least one beyond-Standard Model decays, while the others are strong decays. Branching ratios modification is required. Many precision physics searches to true muonium can be estimated by multiplying by α4 ≈ have been undertaken in the charged lepton sector to de- 2.8 × 10−9 tect additional lepton universality violations. Measure- ments of (g − 2)` [1], charge radii [2,3], and B meson Channel BR decays [4–14] have each shown hints of discrepancy. The −1 + − η → γγ 4.0 × 10 bound state of (µ µ ), true muonium, or TM for short, 0 −2 presents another avenue for investigating lepton univer- η → γγ 2.2 × 10 0 −1 sality [15, 16].
    [Show full text]
  • HEPAP Looks Into the Future
    Volume 20 Friday, August 29, 1997 Number 17 f INSIDE HEPAP Looks into 2 HEPAP: Voice of the Community the Future 5 Profiles in HEPAP subpanel meets at Fermilab to chart the future of Particle Physics: high-energy physics in the U.S. Dave McGinnis by Donald Sena and Sharon Butler, Office of Public Affairs 6 Barns of Fermilab Charged with recommending how best to In a letter to HEPAP, Martha Krebs, position the U.S. particle physics community Director of the U.S. Department of Energy’s for new facilities beyond CERN’s Large Office of Energy Research, directed the Hadron Collider, a subpanel of the High- subpanel to “recommend a scenario for an Energy Physics Advisory Panel met at Fermilab optimal and balanced U.S. high-energy physics August 14-16 to hear presentations on such program over the next decade,” with “new topics as the research agenda for Fermilab’s facilities to address physics opportunities Run II, the complicated upgrades to the CDF beyond the LHC.” She asked the subpanel and DZero detectors and research on future to consider a future course in light of three accelerators. continued on page 3 Photo by Reidar Hahn Dixon Bogert, deputy project manager for the Main Injector, leads a tour for HEPAP subpanel members and DOE officials. HEPAP: Voice of the Community by Donald Sena and Sharon Butler, Office of Public Affairs The High-Energy Physics Advisory In 1983, for example, a HEPAP According to Fermilab physicist Cathy Panel traces its history to the 1960s, subpanel recommended terminating Newman-Holmes, outgoing member of when
    [Show full text]
  • Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems
    Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1222 Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems DANIEL PELIKAN ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6214 ISBN 978-91-554-9153-6 UPPSALA urn:nbn:se:uu:diva-242491 2015 Dissertation presented at Uppsala University to be publicly examined in Polhemssalen, Ångströmlaboratoriet, Lägerhyddsvägen 1, Uppsala, Friday, 20 March 2015 at 10:00 for the degree of Doctor of Philosophy. The examination will be conducted in English. Faculty examiner: Prof. Dr. Fabrizio Palla (Istituto Nazionale di Fisica Nucleare (INFN) Pisa). Abstract Pelikan, D. 2015. Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems. Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1222. 119 pp. Uppsala: Acta Universitatis Upsaliensis. ISBN 978-91-554-9153-6. The discovery of a charged Higgs boson (H±) would be a clear indication for physics beyond the Standard Model. This thesis describes searches for charged Higgs bosons with the ATLAS experiment at CERN’s Large Hadron Collider (LHC). The first data collected during the LHC Run 1 is analysed, searching for a light charged Higgs boson (mH±<mtop), which decays predominantly into a tau-lepton and a neutrino. Different final states with one or two leptons (electrons or muons), as well as leptonically or hadronically decaying taus, are studied, and exclusion limits are set. The background arising from misidentified non-prompt electrons and muons was estimated from data. This so-called "Matrix Method'' exploits the difference in the lepton identification between real, prompt, and misidentified or non-prompt electrons and muons.
    [Show full text]
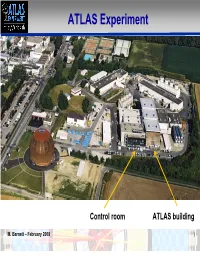
  • ATLAS Experiment
    ATLAS Experiment Control room ATLAS building M. Barnett – February 2008 1 Final piece of ATLAS lowered last Friday (the second small muon wheel) M. Barnett – February 2008 2 M. Barnett – February 2008 3 Still to be done Connecting: Cables, Fibers, Cryogenics M. Barnett – February 2008 4 Celebrations M. Barnett – February 2008 5 News Coverage News media are flooding CERN well in advance of startup "Particle physics is the unbelievable in pursuit of the unimaginable. To pinpoint the smallest fragments of the universe you have to build the biggest machine in the world. To recreate the first millionths of a second of creation you have to focus energy on an awesome scale." The Guardian M. Barnett – February 2008 6 Three full pages in New York Times M. Barnett – February 2008 7 New York Times M. Barnett – February 2008 8 National Geographic Magazine M. Barnett – February 2008 9 National Geographic Magazine M. Barnett – February 2008 10 National Geographic Magazine M. Barnett – February 2008 11 M. Barnett – February 2008 12 M. Barnett – February 2008 13 M. Barnett – February 2008 14 M. Barnett – February 2008 15 M. Barnett – February 2008 16 M. Barnett – February 2008 17 M. Barnett – February 2008 18 M. Barnett – February 2008 19 M. Barnett – February 2008 20 M. Barnett – February 2008 21 M. Barnett – February 2008 22 And on television (shortened version) M. Barnett – February 2008 23 An ATLAS expert explains the Higgs evidence to a layperson. M. Barnett – February 2008 24 US-LHC Student Journalism Program April 2-7, 2008 (overlapping Open Days) Six teams of high school students (3 students/1 teacher) are going to CERN to report on the LHC startup.
    [Show full text]
  • How and Why to Go Beyond the Discovery of the Higgs Boson
    How and Why to go Beyond the Discovery of the Higgs Boson John Alison University of Chicago http://hep.uchicago.edu/~johnda/ComptonLectures.html Lecture Outline April 1st: Newton’s dream & 20th Century Revolution April 8th: Mission Barely Possible: QM + SR April 15th: The Standard Model April 22nd: Importance of the Higgs April 29th: Guest Lecture May 6th: The Cannon and the Camera May 13th: The Discovery of the Higgs Boson May 20th: Problems with the Standard Model May 27th: Memorial Day: No Lecture June 3rd: Going beyond the Higgs: What comes next ? 2 Reminder: The Standard Model Description fundamental constituents of Universe and their interactions Triumph of the 20th century Quantum Field Theory: Combines principles of Q.M. & Relativity Constituents (Matter Particles) Spin = 1/2 Leptons: Quarks: νe νµ ντ u c t ( e ) ( µ) ( τ ) ( d ) ( s ) (b ) Interactions Dictated by principles of symmetry Spin = 1 QFT ⇒ Particle associated w/each interaction (Force Carriers) γ W Z g Consistent theory of electromagnetic, weak and strong forces ... ... provided massless Matter and Force Carriers Serious problem: matter and W, Z carriers have Mass ! 3 Last Time: The Higgs Feild New field (Higgs Field) added to the theory Allows massive particles while preserve mathematical consistency Works using trick: “Spontaneously Symmetry Breaking” Zero Field value Symmetric in Potential Energy not minimum Field value of Higgs Field Ground State 0 Higgs Field Value Ground state (vacuum of Universe) filled will Higgs field Leads to particle masses: Energy cost to displace Higgs Field / E=mc 2 Additional particle predicted by the theory. Higgs boson: H Spin = 0 4 Last Time: The Higgs Boson What do we know about the Higgs Particle: A Lot Higgs is excitations of v-condensate ⇒ Couples to matter / W/Z just like v X matter: e µ τ / quarks W/Z h h ~ (mass of matter) ~ (mass of W or Z) matter W/Z Spin: 0 1/2 1 3/2 2 Only thing we don’t (didn’t!) know is the value of mH 5 History of Prediction and Discovery Late 60s: Standard Model takes modern form.
    [Show full text]
  • Hadron Physics at the Charm and Bottom Thresholds and Other Novel QCD Physics Topics at the NICA Accelerator Facility
    SLAC-PUB-15050 Hadron Physics at the Charm and Bottom Thresholds and Other Novel QCD Physics Topics at the NICA Accelerator Facility Stanley J. Brodsky1 1SLAC National Accelerator Laboratory Stanford University, Stanford, California 94309, USA The NICA collider project at the Joint Institute for Nuclear Research in Dubna will have the capability of colliding protons, polarized deuterons, and nuclei at an effective nucleon-nucleon center- p of mass energy in the range sNN = 4 to 11 GeV. I briefly survey a number of novel hadron physics processes which can be investigated at the NICA collider. The topics include the formation of exotic heavy quark resonances near the charm and bottom thresholds, intrinsic strangeness, charm, and bottom phenomena, hidden-color degrees of freedom in nuclei, color transparency, single-spin asymmetries, the RHIC baryon anomaly, and non-universal antishadowing. I. INTRODUCTION The NICA collider project at the Joint Institute for Nuclear Research in Dubna [1,2] will have the capability of colliding nucleons, polarized deuterons, and nuclei at an effective nucleon-nucleon center-of mass energy in the range p sNN = 4 to 11 GeV. In tis brief report, I will discuss a number of novel hadron physics topics which can be investigated at the NICA collider. The topics include the formation of exotic heavy quark resonances near the charm and bottom thresholds, intrinsic strangeness, charm, and bottom phenomena, hidden-color degrees of freedom in nuclei, color transparency, single-spin asymmetries, the RHIC baryon anomaly, and non-universal antishadowing. II. THE ULTRA-LOW ENERGY DOMAIN USING VARIABLE-ANGLE COLLISIONS If the interaction region at NICA is designed so that A and B can collide at a variable finite center of mass angle 2 2 2 0 < θ < π, then the effective CM energy squared s = (pA + pB) = MA + MB + 2EAEB(1 − βAβB cos θ) will span from very low energies to beyond the bottom flavor threshold.
    [Show full text]
  • Nuclear Criticality Safety Engineer Training Module 1 1
    Nuclear Criticality Safety Engineer Training Module 1 1 Introductory Nuclear Criticality Physics LESSON OBJECTIVES 1) to introduce some background concepts to engineers and scientists who do not have an educational background in nuclear engineering, including the basic ideas of moles, atom densities, cross sections and nuclear energy release; 2) to discuss the concepts and mechanics of nuclear fission and the definitions of fissile and fissionable nuclides. NUCLEAR CRITICALITY SAFETY The American National Standard for Nuclear Criticality Safety in Operations with Fissionable Materials Outside Reactors, ANSI/ANS-8.1 includes the following definition: Nuclear Criticality Safety: Protection against the consequences of an inadvertent nuclear chain reaction, preferably by prevention of the reaction. Note the words: nuclear - related to the atomic nucleus; criticality - can it be controlled, will it run by itself; safety - protection of life and property. DEFINITIONS AND NUMBERS What is energy? Energy is the ability to do work. What is nuclear energy? Energy produced by a nuclear reaction. What is work? Work is force times distance. 1 Developed for the U. S. Department of Energy Nuclear Criticality Safety Program by T. G. Williamson, Ph.D., Westinghouse Safety Management Solutions, Inc., in conjunction with the DOE Criticality Safety Support Group. NCSET Module 1 Introductory Nuclear Criticality Physics 1 of 18 Push a car (force) along a road (distance) and the car has energy of motion, or kinetic energy. Climb (force) a flight of steps (distance) and you have energy of position relative to the first step, or potential energy. Jump down the stairs or out of a window and the potential energy is changed to kinetic energy as you fall.
    [Show full text]
  • Long-Range Beam–Beam Effects in the Tevatron* V
    Published by CERN in the Proceedings of the ICFA Mini-Workshop on Beam–Beam Effects in Hadron Colliders, CERN, Geneva, Switzerland, 18–22 March 2013, edited by W. Herr and G. Papotti, CERN–2014–004 (CERN, Geneva, 2014) LONG-RANGE BEAM–BEAM EFFECTS IN THE TEVATRON* V. Shiltsev#, A.Valishev, FNAL, Batavia, IL, USA Abstract Long-range beam–beam effects occurred in the Tevatron at all stages (injection, ramp, squeeze, and collisions) and affected both proton and antiproton beams. They resulted in beam losses and emittance blow-ups, which occurred in remarkable bunch-to-bunch dependent patterns. On the way to record-high luminosities of the collider, many issues related to the long-range beam– beam interactions have been addressed. Below we present a short overview of the long-range beam–beam effects in the Tevatron. (For a detailed discussion on the beam– beam effects in the Tevatron please see reviews in Refs. [1–3] and references therein). HELICAL ORBITS IN TEVAT R O N Beam–beam interactions in the Tevatron differ between the injection and collision stages. The helical orbits were introduced to provide sufficient separation between the proton and antiproton beams in order to reduce Figure 2: The pattern of the Tevatron helical orbits at the detrimental beam–beam effects, e.g. tune shifts, coupling, collision stage. and high-order resonance driving terms. In 36 × 36 bunch Initially, there were six separator groups (three operation, each bunch experienced 72 long-range horizontal and three vertical) in the arcs between the two interactions per revolution at injection, but at collision main interaction points, B0 (CDF) and D0.
    [Show full text]
  • Redtop-Carosi-1.Pdf
    REDTOP Rare Eta Decays with a TPC for Optical Photons R. Carosi, INFN Pisa Workshop on Physics Beyond Colliders CERN, 16 jan. 2019 For the REDTOP Collaboration REDTOP Key Points ● Yield of 8x1012 h mesons/year for 1017 POT (x-section >10 mbarns, 1.8 GeV proton beam) – Possibly ~8x1010 h’ mesons/years in a second phase (3.5 GeV protons) ● 4p detector coverage (almost) ● 3 (5) “golden” channels (will be described in details in the proposal) – But at least ~20 interesting channels (simmetry violations, new particles and forces searches, precision measurements) – 4 benchmark channels are studied in details for the BPC (2 of them are golden) ● Innovative detector techniques – Dual readout calorimeter – Optical TPC ● Detector blind to protons and slow pions ● Significant improvement (106 in some cases) to the current limits. ● http://redtop.fnal.gov Why the h ? ● Decays are flavor conserving ● Eigenstate of C, P, CP and G: IGJPC=0+0-+ – can be used to test C and CP invariances ● Very narrow state (1.3 keV) – overconstraints events → low background ● Strong decays forbidden in lowest order by C, P, CP, G, and Isospin invariance ● EM decays forbidden in lowest order by C and angular momentum conservation – contributions from higher orders are enhanced by a factor of ~100,000 – h decays with leptons in the final state have very small SM backgrounds – Internal loops and lepton pairs can probe new physics ● h is an excellent laboratory to search for physics Beyond Standard Model BSM Physics Program (h and h’ factory) C, T, CP-violation CP Violation via Dalitz plot mirror asymmetry: h → po p+p- CP Violation (Type I – P and T odd , C even): h-> 4po → 8g CP Violation (Type II - C and T odd , P even): h → po l+l and h → 3g Test of CP invariance via m longitudinal polarization: h → m+m – Test of CP invariance via g* polarization studies:h → p+p –e+e – and h → p+p –m+m– Test of CP invariance in angular correlation studies:h → m+m – e+e – Test of T invariance via m transverse polarization: h → pom+m – and h → g m+m – CPT violation: m polariz.
    [Show full text]