DOCSLIB.ORG

Introduction Joint Facet Tropism Was Previously Defined As the Difference

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction Joint Facet Tropism Was Previously Defined As the Difference 1 Introduction 2 Joint facet tropism was previously defined as the difference between right and left 3D orientation of the facet-joint 3 (Brailsford, 1929). Additionally, spine joints morphology (i.e. surface geometry) has been also shown to be of 4 clinical relevance while possibly determining degenerative processes (e.g. osteoarthritis, degenerative 5 spondylolisthesis) or injury mechanisms of the spine (Liu et al., 2017). Tropism together with facet 3D orientation 6 have been proposed as factors likely associated with laterality of specific diseases in both the lumbar spine (Alonso 7 et al., 2017; Gao et al., 2017; Kalichman et al., 2009) and the cervical spine (Rong et al., 2017b; Xu et al., 2016, 8 2014). However, considering the costovertebral joint complexes which are involved in both respiratory function 9 (Cappello and De Troyer, 2002) and thoracic spine stability (Brasiliense et al., 2011; Liebsch et al., 2017; Oda et 10 al., 1996; Takeuchi et al., 1999; Watkins et al., 2005), it is questionable how tropism could similarly affect costal 11 facets, but literature concerning costal facets remains qualitative (Drake et al., 2010; Moore et al., 2010; Struthers, 12 1874). In addition, costal facet geometry may partly explain the variability in rib motion during breathing 13 movement (Beyer et al., 2016, 2015). Finally, since the costal facets are also related to the orientation of the 14 transverse processes (Bastir et al., 2014; Gray et al., 2005) measurements of 3D morphometric features of both 15 vertebrae and costal facets can contribute to the understanding of functional and clinical aspects of the rib/vertebra 16 relationship. Thus, the aim of the present study was (1) to propose a methodology for determining location and 17 orientation of the costal facet on the transverse process of the thoracic vertebra Th1 to Th10; (2) to test the 18 hypotheses that tropism exists for costal facets as well as serial variation in orientation and shape among different 19 serial thoracic levels and 3) to investigate/explore the serial variation of the costal facet in the context of symmetric 20 and asymmetric features of the of the global vertebrae shape using 3D geometric morphometrics. 21 Material and Methods 22 3D reconstructions, anatomical landmarks and coordinate system 23 Thorax 3D reconstructions from anonymized CT-scan data of previous works (Beyer et al., 2017, 2016, 2015, 24 2014; Cassart et al., 1996) were used in the present study. According to the Helsinki protocol (Goodyear et al., 25 2007) and local Erasme Hospital Ethics Committee (P2005/021), all of the subjects signed a written consent that 26 allowed the use of these data for scientific purposes. A total of 140 vertebrae from Th1 to Th10 from a sample of 27 14 asymptomatic adults (including 6 males and 8 females; mean age 29.8 ± 5.1 years old) were processed. 28 Anatomical landmarks (ALs) were placed on 3D models in order to create a vertebra coordinate system (VCS) on 29 each thoracic vertebra using a custom made software called LhpFuionBox (http://lhpfusionbox.org/). The ALs 30 were located following adaptation of the method described in previous work (Beyer et al., 2016, 2015) but details 31 concerning ALs and axes of the coordinate system are depicted in figure 1. 32 Figure 1 33 Costal facet landmarks and geometry 34 A series of points (in average 95±43) were placed on the left and right costal facet of each thoracic vertebra (see 35 figure 2). Costal facet landmarks (CFLs) were occasionally undetermined at Th1 (21%), Th9 (4%) or Th10 (43%) 36 on a single or both sides, and eventually a total of 258 costal facets were analyzed. For most accurately determining 37 the location of the costal facet, the combination of both 3D models and CT slices were analyzed (see figure 2). 1 38 The CFLs were equally distributed on the entire joint facet and were then all expressed in the local vertebra 39 coordinate system (VCS). Figure 2 40 All feature calculations were performed by using in-house software implemented in the Matlab R 2014b platform 41 (MathWorks,Natick, Massachusetts). Spatial coordinates of the ALs and CFLs were processed as follows. Left 42 ALs coordinates were mirrored to the right side (Meskers et al., 1998) through the sagittal plane formed by the x- 43 axis and y-axis in order to compare right and left geometrical parameters of the costal facets. Spatial orientation 44 and location of the costal facet was determined as follows. First, the centroid of the CFLs of each costal facet was 45 computed. Second, a plane crossing the surface centroid was fitted to CFLs by minimizing orthogonal distance of 46 ALs to the plane using least-squares regression (see figure 2). The root mean square (RMS) distances from ALs 47 to the plane were calculated to estimate the out-of-plane deviation of the shape of the costal facet. In other words: 48 the greater the RMS the more concave the costal facet; and the smaller the RMS the flatter the facet. Third, a 3D 49 vector orthogonal to the best-fitted plane was computed to describe the 3D orientation of the joint facet. Finally, 50 orientation of the latter vector was expressed using inclination angle α (sagittal orientation) and declination angle 51 β (transverse orientation) as shown in the bottom of figure 3. A positive value for α and β angles corresponds to 52 superior and anterior orientation, respectively. Facet tropism was then estimated according to the absolute 53 difference between left and right values of both inclination and declination angles. To ensure the reproducibility 54 of the measurements, 40 costal facets of 20 vertebrae from 2 subjects were measured by a single observer at three 55 different sessions with more than 24 hours apart. Then, the mean standard deviation and coefficient of variation 56 were calculated for inclination and declination angle as well as for the distance from the best fit plane. 57 Figure 3 58 Statistical analysis 59 Statistical analysis was performed using Statistica software (Statistica 8.0© StatSoft. Inc., Tulsa, USA). Normality 60 test Kolmogorov-Smirnov was performed to evaluate data distribution. All variables followed normal distribution. 61 In order to evaluate the tropism, the averaged absolute difference between right and left measurements (i.e. 62 inclination and declination angles) was tested in a one-sample t-test against a fixed mean value of 0° which 63 corresponds to absolute symmetry. Values of p<0.05 were considered statistically significant. An analysis of 64 variance (ANOVA) was then used to estimate the difference between serial thoracic levels (Th1 to Th10). When 65 ANOVA demonstrated a significant effect, Tukey post-hoc test was used to determine the significant differences 66 at p=0.05. 67 3D Geometric Morphometric and Procrustes analysis on overall vertebra shape 68 The above-mentioned set of 16 landmarks (14 virtually placed and 2 additional ones computed as the centroid of 69 the costal facet) of the remaining 128 vertebra were used to determine shape variations of the thoracic vertebra in 70 relation to the location of the costal facet using the standard 3D geometric morphometric (GM) analysis 71 (O’Higgins, 2000; Zelditch et al., 2004). The 3D GM approach enables analysis of 3D shape using homologous 72 vertebra ALs defined above (Bookstein, 1997; Zelditch et al., 2004). In a geometric morphometric shape analysis 73 all specimens are measured by the same set of homologue landmarks leading to landmark configurations that are 74 subject to Generalized Procrustes Analysis (GPA) (Gower, 1975). GPA removes information of the landmark 75 coordinates related orientation, position and scale. By applying iterative least squares based registrations using 76 rotation, translation and rescaling, GPA minimizes the distances among homologous landmarks using of the 2 77 landmark configurations relative their mean shape (consensus) leading to a set of shape coordinates and a size 78 variable (centroid size) (Zelditch et al., 2004). After GPA, the shape coordinates can be analyzed by standardized 79 multivariate statistical analyses addressing specific hypotheses (Mitteroecker and Gunz, 2009). One key advantage 80 of GM over other morphometric methods is the direct correspondence of each specimen in shape space with a 81 given landmark configuration, which allows for powerful visualizations of statistical results (Zelditch et al., 2004). 82 Geometric morphometrics have been used to investigate symmetry and asymmetry (Klingenberg, 2015). To obtain 83 the symmetric and asymmetric components of total shape variation a method called “reflected relabeling” (Mardia 84 et al., 2000) is applied in which the original landmarks data of the full vertebrae are superimposed onto its mirrored 85 landmarks. Principal components analyses (PCA) were then carried out on the symmetric and on the asymmetric 86 components of shape data (Mitteroecker and Gunz, 2009) to investigate the seriality (that is, 3D shape change 87 between different serial levels). 88 With respect to the symmetric component we projected the shape data onto the first two principal components and 89 explore overall symmetric shape changes related to seriality. With respect to the more subtle, asymmetric part of 90 shape variation, we performed a second PCA followed by an ANOVA on the PC scores of the first three PC- 91 scores. This analysis was used to explore a potential systemic trend in asymmetry along different serial thoracic 92 vertebral levels. 93 94 Results 95 All tables of descriptive statistic are available in supplementary material. Results of the reproducibility analysis 96 displayed a mean standard deviation of 0.6 mm for the deviation from the best fit plane, 1.8° for inclination angle 97 and 1.9° for declination angle. Respectively, measurements showed a coefficient of variation of 15.6%, 9.0% and 98 5.6%.
Load more

Recommended publications
  • The Structure and Function of Breathing
    CHAPTERCONTENTS The structure-function continuum 1 Multiple Influences: biomechanical, biochemical and psychological 1 The structure and Homeostasis and heterostasis 2 OBJECTIVE AND METHODS 4 function of breathing NORMAL BREATHING 5 Respiratory benefits 5 Leon Chaitow The upper airway 5 Dinah Bradley Thenose 5 The oropharynx 13 The larynx 13 Pathological states affecting the airways 13 Normal posture and other structural THE STRUCTURE-FUNCTION considerations 14 Further structural considerations 15 CONTINUUM Kapandji's model 16 Nowhere in the body is the axiom of structure Structural features of breathing 16 governing function more apparent than in its Lung volumes and capacities 19 relation to respiration. This is also a region in Fascla and resplrstory function 20 which prolonged modifications of function - Thoracic spine and ribs 21 Discs 22 such as the inappropriate breathing pattern dis- Structural features of the ribs 22 played during hyperventilation - inevitably intercostal musculature 23 induce structural changes, for example involving Structural features of the sternum 23 Posterior thorax 23 accessory breathing muscles as well as the tho- Palpation landmarks 23 racic articulations. Ultimately, the self-perpetuat- NEURAL REGULATION OF BREATHING 24 ing cycle of functional change creating structural Chemical control of breathing 25 modification leading to reinforced dysfunctional Voluntary control of breathing 25 tendencies can become complete, from The autonomic nervous system 26 whichever direction dysfunction arrives, for Sympathetic division 27 Parasympathetic division 27 example: structural adaptations can prevent NANC system 28 normal breathing function, and abnormal breath- THE MUSCLES OF RESPIRATION 30 ing function ensures continued structural adap- Additional soft tissue influences and tational stresses leading to decompensation.
    [Show full text]
  • Managing a Rib Fracture: a Patient Guide
    Managing a Rib Fracture A Patient Guide What is a rib fracture? How is a fractured rib diagnosed? A rib fracture is a break of any of the bones that form the Your doctor will ask questions about your injury and do a rib cage. There may be a single fracture of one or more ribs, physical exam. or a rib may be broken into several pieces. Rib fractures are The doctor may: usually quite painful as the ribs have to move to allow for normal breathing. • Push on your chest to find out where you are hurt. • Watch you breathe and listen to your lungs to make What is a flail chest? sure air is moving in and out normally. When three or more neighboring ribs are fractured in • Listen to your heart. two or more places, a “flail chest” results. This creates an • Check your head, neck, spine, and belly to make sure unstable section of chest wall that moves in the opposite there are no other injuries. direction to the rest of rib cage when you take a breath. • You may need to have an X-ray or other imaging test; For example, when you breathe in your rib cage rises out however, rib fractures do not always show up on X-rays. but the flail chest portion of the rib cage will actually fall in. So you may be treated as though you have a fractured This limits your ability to take effective deep breaths. rib even if an X-ray doesn’t show any broken bones.
    [Show full text]
  • Ligaments of the Costovertebral Joints Including Biomechanics, Innervations, and Clinical Applications: a Comprehensive Review W
    Open Access Review Article DOI: 10.7759/cureus.874 Ligaments of the Costovertebral Joints including Biomechanics, Innervations, and Clinical Applications: A Comprehensive Review with Application to Approaches to the Thoracic Spine Erfanul Saker 1 , Rachel A. Graham 2 , Renee Nicholas 3 , Anthony V. D’Antoni 2 , Marios Loukas 1 , Rod J. Oskouian 4 , R. Shane Tubbs 5 1. Department of Anatomical Sciences, St. George's University School of Medicine, Grenada, West Indies 2. Department of Anatomy, The Sophie Davis School of Biomedical Education 3. Department of Physical Therapy, Samford University 4. Neurosurgery, Complex Spine, Swedish Neuroscience Institute 5. Neurosurgery, Seattle Science Foundation Corresponding author: Erfanul Saker, [email protected] Abstract Few studies have examined the costovertebral joint and its ligaments in detail. Therefore, the following review was performed to better elucidate their anatomy, function and involvement in pathology. Standard search engines were used to find studies concerning the costovertebral joints and ligaments. These often- overlooked ligaments of the body serve important functions in maintaining appropriate alignment between the ribs and spine. With an increasing interest in minimally invasive approaches to the thoracic spine and an improved understanding of the function and innervation of these ligaments, surgeons and clinicians should have a good working knowledge of these structures. Categories: Neurosurgery, Orthopedics, Rheumatology Keywords: costovertebral joint, spine, anatomy, thoracic Introduction And Background The costovertebral joint ligaments are relatively unknown and frequently overlooked anatomical structures [1]. Although small and short in size, they are abundant, comprising 108 costovertebral ligaments in the normal human thoracic spine, and they are essential to its stability and function [2-3].
    [Show full text]
  • Copyrighted Material
    C01 10/31/2017 11:23:53 Page 1 1 1 The Normal Anatomy of the Neck David Bainbridge Introduction component’ of the neck is a common site of pathology, and the diverse forms of neck The neck is a common derived characteristic disease reflect the sometimes complex and of land vertebrates, not shared by their aquatic conflicting regional variations and functional ancestors. In fish, the thoracic fin girdle, the constraints so evident in this region [2]. precursor of the scapula, coracoid and clavi- Unlike the abdomen and thorax, there is no cle, is frequently fused to the caudal aspect of coelomic cavity in the neck, yet its ventral part the skull. In contrast, as vertebrates emerged is taken up by a relatively small ‘visceral on to the dry land, the forelimb separated from compartment’, containing the larynx, trachea, the head and the intervening vertebrae speci- oesophagus and many important vessels, alised to form a relatively mobile region – the nerves and endocrine glands. However, I neck – to allow the head to be freely steered in will not review these structures, as they do many directions. not represent an extension of the equine ‘back’ With the exception of the tail, the neck in the same way that the more dorsal locomo- remains the most mobile region of the spinal tor region does. column in modern-day horses. It permits a wide range of sagittal plane flexion and exten- sion to allow alternating periods of grazing Cervical Vertebrae 3–7 and predator surveillance, as well as frontal plane flexion to allow the horizon to be scan- Almost all mammals, including the horse, ned, and rotational movement to allow possess seven cervical vertebrae, C1 to C7 nuisance insects to be flicked off.
    [Show full text]
  • Part 1 the Thorax ECA1 7/18/06 6:30 PM Page 2 ECA1 7/18/06 6:30 PM Page 3
    ECA1 7/18/06 6:30 PM Page 1 Part 1 The Thorax ECA1 7/18/06 6:30 PM Page 2 ECA1 7/18/06 6:30 PM Page 3 Surface anatomy and surface markings The experienced clinician spends much of his working life relating the surface anatomy of his patients to their deep structures (Fig. 1; see also Figs. 11 and 22). The following bony prominences can usually be palpated in the living subject (corresponding vertebral levels are given in brackets): •◊◊superior angle of the scapula (T2); •◊◊upper border of the manubrium sterni, the suprasternal notch (T2/3); •◊◊spine of the scapula (T3); •◊◊sternal angle (of Louis) — the transverse ridge at the manubrio-sternal junction (T4/5); •◊◊inferior angle of scapula (T8); •◊◊xiphisternal joint (T9); •◊◊lowest part of costal margin—10th rib (the subcostal line passes through L3). Note from Fig. 1 that the manubrium corresponds to the 3rd and 4th thoracic vertebrae and overlies the aortic arch, and that the sternum corre- sponds to the 5th to 8th vertebrae and neatly overlies the heart. Since the 1st and 12th ribs are difficult to feel, the ribs should be enu- merated from the 2nd costal cartilage, which articulates with the sternum at the angle of Louis. The spinous processes of all the thoracic vertebrae can be palpated in the midline posteriorly, but it should be remembered that the first spinous process that can be felt is that of C7 (the vertebra prominens). The position of the nipple varies considerably in the female, but in the male it usually lies in the 4th intercostal space about 4in (10cm) from the midline.
    [Show full text]
  • National Imaging Associates, Inc. Clinical Guidelines FACET JOINT
    National Imaging Associates, Inc. Clinical guidelines Original Date: July 1, 2015 FACET JOINT INJECTIONS OR BLOCKS Page 1 of 4 “FOR FLORIDA BLUE MEMBERS ONLY” CPT Codes: Last Review Date: May 28, 2015 Cervical/Thoracic Region: 64490 (+ 64491, +64492) Lumbar/Sacral Region: 64493 (+64494, +64495) Medical Coverage Guideline Number: Last Revised Date: 02-61000-30 Responsible Department: Implementation Date: July 2015 Clinical Operations “FOR FLORIDA BLUE MEMBERS ONLY” INTRODUCTION Facet joints (also called zygapophysial joints or z-joints), are posterior to the vertebral bodies in the spinal column and connect the vertebral bodies to each other. They are located at the junction of the inferior articular process of a more cephalad vertebra, and the superior articular process of a more caudal vertebra. These joints provide stability and enable movement, allowing the spine to bend, twist, and extend in different directions. They also restrict hyperextension and hyperflexion. Facet joints are clinically important spinal pain generators in those with chronic spinal pain. Facet joints may refer pain to adjacent structures, making the underlying diagnosis difficult, as referred pain may assume a pseudoradicular pattern. Lumbar facet joints may refer pain to the back, buttocks, and lower extremities while cervical facet joints may refer pain to the head, neck and shoulders. Imaging findings are of little value in determining the source and location of ‘facet joint syndrome’, a term referring to back pain caused by pathology at the facet joints. Imaging studies may detect changes in facet joint architecture, but correlation between radiologic findings and symptoms is unreliable. Although clinical signs are also unsuitable for diagnosing facet joint-mediated pain, they may be of value in selecting candidates for controlled local anesthetic blocks of either the medial branches or the facet joint itself.
    [Show full text]
  • The Erector Spinae Plane Block a Novel Analgesic Technique in Thoracic Neuropathic Pain
    CHRONIC AND INTERVENTIONAL PAIN BRIEF TECHNICAL REPORT The Erector Spinae Plane Block A Novel Analgesic Technique in Thoracic Neuropathic Pain Mauricio Forero, MD, FIPP,*Sanjib D. Adhikary, MD,† Hector Lopez, MD,‡ Calvin Tsui, BMSc,§ and Ki Jinn Chin, MBBS (Hons), MMed, FRCPC|| Case 1 Abstract: Thoracic neuropathic pain is a debilitating condition that is often poorly responsive to oral and topical pharmacotherapy. The benefit A 67-year-old man, weight 116 kg and height 188 cm [body of interventional nerve block procedures is unclear due to a paucity of ev- mass index (BMI), 32.8 kg/m2] with a history of heavy smoking idence and the invasiveness of the described techniques. In this report, we and paroxysmal supraventricular tachycardia controlled on ateno- describe a novel interfascial plane block, the erector spinae plane (ESP) lol, was referred to the chronic pain clinic with a 4-month history block, and its successful application in 2 cases of severe neuropathic pain of severe left-sided chest pain. A magnetic resonance imaging (the first resulting from metastatic disease of the ribs, and the second from scan of his thorax at initial presentation had been reported as nor- malunion of multiple rib fractures). In both cases, the ESP block also pro- mal, and the working diagnosis at the time of referral was post- duced an extensive multidermatomal sensory block. Anatomical and radio- herpetic neuralgia. He reported constant burning and stabbing logical investigation in fresh cadavers indicates that its likely site of action neuropathic pain of 10/10 severity on the numerical rating score is at the dorsal and ventral rami of the thoracic spinal nerves.
    [Show full text]
  • Evaluation and Treatment of Selected Sacral Somatic Dysfunctions
    Evaluation and Treatment of Selected Sacral Somatic Dysfunctions Using Direct and HVLA Techniques including Counterstrain and Muscle Energy AND Counterstrain Treatment of the Pelvis and Sacrum F. P. Wedel, D.O. Associate Adjunct Professor in Osteopathic Principles and Practice A.T. Still University School of Osteopathic Medicine in Arizona, and private practice in Family Medicine in Tucson, Arizona Learning Objectives HOURS 1 AND 2 Review the following diagnostic and treatment techniques related to sacral torsion Lumbosacral spring test Sacral palpation Seated flexion test HOURS 3 AND 4 Counterstrain treatments of various low back pathologies Sacral Techniques Covered : 1. Prone, direct, muscle energy, for sacral rotation on both same and opposite axes 2. HVLA treatment for sacral rotation on both same and opposite axes 3. Counterstain treatment of sacral tender points and of sacral torsion Counterstrain Multifidi and Rotatores : UP5L Gluteii – maximus: HFO-SI, HI, P 3L- P 4L ,medius, minimus Piriformis Background and Basis The 4 Osteopathic Tenets (Principles) 1. The body is a unit; the person is a unit of body, mind, and spirit. 2. Structure and function are reciprocally inter-related. 3. The body is capable of self- regulation, self-healing, and health maintenance. 4. Rational treatment is based upon an understanding of these basic principles. Somatic Dysfunction - Defined • “Impaired or altered function of related components of the somatic (body framework) system: • Skeletal, arthrodial, and myofascial structures, • And… • Related vascular, lymphatic, and neural elements” Treatment Options for Somatic Dysfunctions All somatic dysfunctions have a restrictive barrier which are considered “pathologic” This restriction inhibits movement in one direction which causes asymmetry within the joint: The goal of osteopathic treament is to eliminate the restrictive barrier thus restoring symmetry….
    [Show full text]
  • Skeletal System? Skeletal System Chapters 6 & 7 Skeletal System = Bones, Joints, Cartilages, Ligaments
    Warm-Up Activity • Fill in the names of the bones in the skeleton diagram. Warm-Up 1. What are the 4 types of bones? Give an example of each. 2. Give 3 ways you can tell a female skeleton from a male skeleton. 3. What hormones are involved in the skeletal system? Skeletal System Chapters 6 & 7 Skeletal System = bones, joints, cartilages, ligaments • Axial skeleton: long axis (skull, vertebral column, rib cage) • Appendicular skeleton: limbs and girdles Appendicular Axial Skeleton Skeleton • Cranium (skull) • Clavicle (collarbone) • Mandible (jaw) • Scapula (shoulder blade) • Vertebral column (spine) • Coxal (pelvic girdle) ▫ Cervical vertebrae • Humerus (arm) ▫ Thoracic vertebrae • Radius, ulna (forearm) ▫ Lumbar vertebrae • Carpals (wrist) • Metacarpals (hand) ▫ Sacrum • Phalanges (fingers, toes) ▫ Coccyx • Femur (thigh) • Sternum (breastbone) • Tibia, fibula (leg) • Ribs • Tarsal, metatarsals (foot) • Calcaneus (heel) • Patella (knee) Functions of the Bones • Support body and cradle soft organs • Protect vital organs • Movement: muscles move bones • Storage of minerals (calcium, phosphorus) & growth factors • Blood cell formation in bone marrow • Triglyceride (fat) storage Classification of Bones 1. Long bones ▫ Longer than they are wide (eg. femur, metacarpels) 2. Short bones ▫ Cube-shaped bones (eg. wrist and ankle) ▫ Sesamoid bones (within tendons – eg. patella) 3. Flat bones ▫ Thin, flat, slightly curved (eg. sternum, skull) 4. Irregular bones ▫ Complicated shapes (eg. vertebrae, hips) Figure 6.2 • Adult = 206 bones • Types of bone
    [Show full text]
  • Pain Pattern Explanation Forms
    Pain Pattern Explanation Forms 1. Cervical Facet Pain Pattern 2. Cervical Radicular/Dynatome Pain Pattern 3. Costotransverse Joint Pain Pattern 4. Fibromyalgia Points 5. Hip Joint Pain Pattern 6. Lumbar Dermatomes: Chemical Radiculitis 7. Lumbar Dermatomes: Disc Pathology 8. Lumbar Disc Pathology Healed 9. Lumbar Epidural Fibrosis 10. Lumbar Facet Pain Pattern 11. Lumbar Stenosis 12. Sacroiliac Joint Pain Pattern 13. Thoracic Facet Pain Pattern 14. Upper Cervical Joint Pain Pattern The OEA pain pattern handouts are PDF files that can be used for patient education and marketing. They help you explain your diagnosis with original illustrations that the patients can take home with them. There is limited text so you can tell your explanation of the treatment plan. The pain patterns can be printed in color or black and white. Once purchased, our business card will be replaced with yours to personalize each handout. Each illustration is based on the pain patterns that have been established in books or research articles when available. Normal anatomy and pathoanatomy illustrations are shown for the clinician to explain the diagnosis to the patient and how their treatment can influence the pain generator. These can also be utilized as marketing tools. The following pages are some guidelines that can be utilized to explain the handouts to patients. Cervical Facet Pain Pattern The cervical facet joints are the joints of the neck. Neurophysiologic studies have shown that cervical facet‐joint capsules are sources of neck pain.1 Dwyer et al.2 established pain patterns of the cervical facet joints. o Parasagittal cervical and cervicothoracic pain.
    [Show full text]
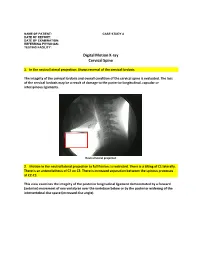
  • Digital Motion X-Ray Cervical Spine
    NAME OF PATIENT: CASE STUDY 4 DATE OF REPORT: DATE OF EXAMINATION: REFERRING PHYSICIAN: TESTING FACILITY: Digital Motion X-ray Cervical Spine 1. In the neutral lateral projection: Shows reversal of the cervical lordosis. The integrity of the cervical lordosis and overall condition of the cervical spine is evaluated. The loss of the cervical lordosis may be a result of damage to the posterior longitudinal, capsular or interspinous ligaments. Neutral lateral projection 2. Motion in the neutral lateral projection to full flexion: Is restricted. There is a tilting of C1 laterally. There is an anterolisthesis of C2 on C3. There is increased separation between the spinous processes at C2-C3. This view examines the integrity of the posterior longitudinal ligament demonstrated by a forward (anterior) movement of one vertebrae over the vertebrae below or by the posterior widening of the intervertebral disc space (increased disc angle). Widening of posterior disc space Anterolisthesis The integrity of the interspinous ligament is evaluated in the lateral flexion view. Damage to this ligament results in increased separation of the spinous processes in flexion. Damaged Interspinous Ligament Full flexion projection 3. Motion in the neutral lateral projection to full extension: Is restricted. There is a retrolisthesis of C4 on C5. This view examines the integrity of the anterior longitudinal ligament demonstrated by a backward (posterior) movement of one vertebrae over the vertebrae below or by the anterior widening of the intervertebral disc space (increased disc angle). Retrolisthesis Widening of the anterior disc Full Extension 4. Motion in the oblique flexion projection: Is restricted. There is gapping of the facet joints at C6-C7 bilaterally and C7-T1 bilaterally.
    [Show full text]
  • The Influence of the Rib Cage on the Static and Dynamic Stability
    www.nature.com/scientificreports OPEN The infuence of the rib cage on the static and dynamic stability responses of the scoliotic spine Shaowei Jia1,2, Liying Lin3, Hufei Yang2, Jie Fan2, Shunxin Zhang2 & Li Han3* The thoracic cage plays an important role in maintaining the stability of the thoracolumbar spine. In this study, the infuence of a rib cage on static and dynamic responses in normal and scoliotic spines was investigated. Four spinal fnite element (FE) models (T1–S), representing a normal spine with rib cage (N1), normal spine without rib cage (N2), a scoliotic spine with rib cage (S1) and a scoliotic spine without rib cage (S2), were established based on computed tomography (CT) images, and static, modal, and steady-state analyses were conducted. In S2, the Von Mises stress (VMS) was clearly decreased compared to S1 for four bending loadings. N2 and N1 showed a similar VMS to each other, and there was a signifcant increase in axial compression in N2 and S2 compared to N1 and S1, respectively. The U magnitude values of N2 and S2 were higher than in N1 and S1 for fve loadings, respectively. The resonant frequencies of N2 and S2 were lower than those in N1 and S1, respectively. In steady-state analysis, maximum amplitudes of vibration for N2 and S2 were signifcantly larger than N1 and S1, respectively. This study has revealed that the rib cage improves spinal stability in vibrating environments and contributes to stability in scoliotic spines under static and dynamic loadings. Scoliosis, a three-dimensional deformity, prevents healthy development.
    [Show full text]