SAME but DIFFERENT: Chaos and TV Drama Narratives
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Slate.Com Table of Contents Faith-Based a Skeptic's Guide to Passover
Slate.com Table of Contents faith-based A Skeptic's Guide to Passover fighting words ad report card Telling the Truth About the Armenian Genocide Credit Crunch foreigners Advanced Search Why Israel Will Bomb Iran books foreigners Why Write While Israel Burns? Too Busy To Save Darfur change-o-meter foreigners Supplemental Diet No Nukes? No Thanks. change-o-meter gabfest Unclenched Fists The Velvet Snuggie Gabfest change-o-meter grieving Dogfights Ahead The Long Goodbye change-o-meter human guinea pig Big Crowds, Few Promises Where There's E-Smoke … chatterbox human nature A Beat-Sweetener Sampler Sweet Surrender corrections human nature Corrections Deeper Digital Penetration culture gabfest jurisprudence The Culture Gabfest, Empty Calories Edition Czar Obama dear prudence jurisprudence It's a Jungle Down There Noah Webster Gives His Blessing drink jurisprudence Not Such a G'Day Spain's Most Wanted: Gonzales in the Dock dvd extras moneybox Wauaugh! And It Can't Count on a Bailout explainer movies Getting High by Going Down Observe and Report explainer music box Heated Controversy When Rock Stars Read Edmund Spenser explainer music box Why Is Gmail Still in Beta? Kings of Rock explainer my goodness It's 11:48 a.m. Do You Know Where Your Missile Is? Push a Button, Change the World faith-based other magazines Passionate Plays In Facebook We Trust faith-based poem Why Was Jesus Crucified? "Bombs Rock Cairo" Copyright 2007 Washingtonpost.Newsweek Interactive Co. LLC 1/125 politics today's papers U.S. Department of Blogging Daring To Dream It's -

2014 DGA Episodic Director Diversity Report (By SIGNATORY COMPANY)
2014 DGA Episodic Director Diversity Report (by SIGNATORY COMPANY) Signatory Company Title Total # of Combined # Combined # Episodes Male # Episodes Male # Episodes Female # Episodes Female Network Episodes Women + Women + Directed by Caucasian Directed by Minority Directed by Caucasian Directed by Minority Minority Minority % Male % Male % Female % Female % Episodes Caucasian Minority Caucasian Minority 50/50 Productions, LLC Workaholics 13 0 0% 13 100% 0 0% 0 0% 0 0% Comedy Central ABC Studios Betrayal 12 1 8% 11 92% 0 0% 1 8% 0 0% ABC ABC Studios Castle 23 3 13% 20 87% 1 4% 2 9% 0 0% ABC ABC Studios Criminal Minds 24 8 33% 16 67% 5 21% 2 8% 1 4% CBS ABC Studios Devious Maids 13 7 54% 6 46% 2 15% 4 31% 1 8% Lifetime ABC Studios Grey's Anatomy 24 7 29% 17 71% 1 4% 2 8% 4 17% ABC ABC Studios Intelligence 12 4 33% 8 67% 4 33% 0 0% 0 0% CBS ABC Studios Mixology 12 0 0% 13 108% 0 0% 0 0% 0 0% ABC ABC Studios Revenge 22 6 27% 16 73% 0 0% 6 27% 0 0% ABC And Action LLC Tyler Perry's Love Thy Neighbor 52 52 100% 0 0% 52 100% 0 0% 0 0% OWN And Action LLC Tyler Perry's The Haves and 36 36 100% 0 0% 36 100% 0 0% 0 0% OWN The Have Nots BATB II Productions Inc. Beauty & the Beast 16 1 6% 15 94% 0 0% 1 6% 0 0% CW Black Box Productions, LLC Black Box, The 13 4 31% 9 69% 0 0% 4 31% 0 0% ABC Bling Productions Inc. -

YHWH's Absence Or Hostility As Two Main Motifs of Suffering and Protest
YHWH’s absence or hostility as two main motifs of suffering and protest in lament psalms A Theo-dramatic approach By Bujorel Lucaci A thesis submitted in partial fulfillment Of the requirement for the degree of Master of Arts Melbourne College of Divinity Date 25. 03. 2011 Acknowledgement Declaration This thesis submitted for assessment is the result of my own work, and no unacknowledged assistance has been received in its planning, drafting, execution or writing. All sources on which it is based have been acknowledged in writing, as has the supervision which I received in the process of its preparation. Name: Bujorel Lucaci Signature: Date: 25 March 2011 i ABSTRACT This thesis seeks to develop a new method of interpretation for lament psalms and to apply it to Psalms 13, 22, 44, 88. The new method is called Theo-dramatic approach. This method recognizes lament psalms as dialogical prayers, (multi- voicing) which describe the drama of suffering experienced by the psalmists. The Theo-dramatic approach is an imaginative method of interpretation. The most important elements are: the script, the theatre and the performance. The actors are: God, the supplicant, the enemy, the community. Script : lament Psalms: 13, 22, 44, and 88, were chosen because they demonstrate much of the vocabulary of the absence or hostility of God. Theatre : the public space provided by the covenant relationship between God and pray-er. Performance : the dramatized grief and pain of the psalmist, caused by the hostility or absence of God. This method of interpretation emphasizes the drama presented in the script: protest, argument, accusation of God for being unfaithful to the covenantal responsibilities. -

Imta Alum Adrianne Palicki Soldiers on in Gi Joe: Retaliation
IMTA ALUM ADRIANNE PALICKI SOLDIERS ON IN GI JOE: RETALIATION IMTA Press Release March 27, 2013 GI Joe: Retaliation opens nationwide Thursday, March 28 “I’ve never trained like this in my life. It’s so much fun…I’m getting paid to get fit, learn how to shoot guns, play soldier, learn to dance…it’s all fun!” – Adrianne Palicki In the 12 years since IMTA alum Adrianne Palicki attended IMTA, she has compiled a complex résumé of TV and film roles playing strong, compelling women such as Tyra Collette on “Friday Night Lights,” Charlie in Legion, Toni Walsh in the re-make of Red Dawn, and Diana Prince in the TV pilot for “Wonder Woman.” The Ohio native, who came to the NY01 IMTA with Margaret O’Brien’s/Starbound (now SB Entertainment Group), is adding a new character to that list of as Lady Jaye in G.I. Joe: Retaliation, the sequel to 2009’s G.I. Joe: The Rise of Cobra. G.I. Joe: Retaliation takes up where the first movie ended, with criminal master of disguise, Zartan, still in the White House and masquerading as the president. Zartan orders the execution of what turns out to be most of the Joe team from the first film – which leaves just Lady Jaye, Roadblock (Dwayne Johnson), Flint (D.J. Cotrona) and Snake Eyes (Ray Park) left to figure out what just happened. Channing Tatum also stars in the film, reprising his role from the first movie as Captain Duke Hauser, and Bruce Willis stars as the original Joe, General Joe Colton. -

Television Academy
Television Academy 2014 Primetime Emmy Awards Ballot Outstanding Directing For A Comedy Series For a single episode of a comedy series. Emmy(s) to director(s). VOTE FOR NO MORE THAN FIVE achievements in this category that you have seen and feel are worthy of nomination. (More than five votes in this category will void all votes in this category.) 001 About A Boy Pilot February 22, 2014 Will Freeman is single, unemployed and loving it. But when Fiona, a needy, single mom and her oddly charming 11-year-old son, Marcus, move in next door, his perfect life is about to hit a major snag. Jon Favreau, Director 002 About A Boy About A Rib Chute May 20, 2014 Will is completely heartbroken when Sam receives a job opportunity she can’t refuse in New York, prompting Fiona and Marcus to try their best to comfort him. With her absence weighing on his mind, Will turns to Andy for his sage advice in figuring out how to best move forward. Lawrence Trilling, Directed by 003 About A Boy About A Slopmaster April 15, 2014 Will throws an afternoon margarita party; Fiona runs a school project for Marcus' class; Marcus learns a hard lesson about the value of money. Jeffrey L. Melman, Directed by 004 Alpha House In The Saddle January 10, 2014 When another senator dies unexpectedly, Gil John is asked to organize the funeral arrangements. Louis wins the Nevada primary but Robert has to face off in a Pennsylvania debate to cool the competition. Clark Johnson, Directed by 1 Television Academy 2014 Primetime Emmy Awards Ballot Outstanding Directing For A Comedy Series For a single episode of a comedy series. -

Kontakt: Peter Sølvsten Thomsen, [email protected] Angel Films
Angel Films præsenterer Premiere: 22. juni Længde: 87 minutter Censur: Tilladt for alle men frarådes børn under syv år. Instruktør: Jeffrey Blitz Skuespillere: Anna Kendrick, Lisa Kudrow, Craig Robinson Premierebiografer: CinemaxX KøBenhavn, CinemaxX Odense, CinemaxX Århus, Nordisk Film Biografer Palads, Nordisk Film Biografer Århus, Kino 1-2-3 Thisted, Atlas Biograferne Rødovre, Lalandia Bio, Nicolai Biograf & Cafe Kontakt: Peter Sølvsten Thomsen, [email protected] Synopsis: Eloise (Anna Kendrick) inviteres til sin bedste venindes bryllup, hvor Eloises ex-kæreste Teddy uheldigvis er forlover. På grund af den pinlige situation er Eloise blevet “degraderet” til bord nummer 19 ved bryllupsfesten. Her deler hun bord med fem andre gæster, som hun ikke kender. Fælles for dem alle er dog, at de er gæster, som kun modvilligt blev inviteret til brylluppet, og som brudeparret inderst inde havde håbet ikke ville dukke op. Men Eloise er fast besluttet på at vise, at hun ikke er sådan at slå ud! Udvidet pressemateriale kan hentes på www.angelfilms.dk Kontakt: Peter Sølvsten Thomsen, [email protected] FOX SEARCHLIGHT PICTURES presents In Association with 3311 PRODUCTIONS A 21 LAPS Production ANNA KENDRICK CRAIG ROBINSON JUNE SQUIBB LISA KUDROW STEPHEN MERCHANT TONY REVOLORI WYATT RUSSELL AMANDA CREW DIRECTED BY ....................................................................... JEFFREY BLITZ SCREENPLAY BY ................................................................. JEFFREY BLITZ STORY BY ............................................................................. -

Friday Night Lights 5X13 - Always.Pdf
Executive Producer: Peter Berg Script #: 513 Executive Producer: Jason Katims Episode #: 426 Executive Producer: David Nevins Production#: 04026 Executive Producer: Brian Grazer Executive Producer: Sarah Aubrey Executive Producer: David Hudgins Co-Executive Producer: Patrick Massett & John Zinman Co-Executive Producer: Bridget Carpenter Co-Executive Producer: John Cameron FRIDAY NIGHT LIGHTS "Always" Written by Jason Katims Directed by Michael Waxman PRODUCTION DRAFT July 9, 2010 July 12, 2010 Blue Pages: Sets,8,9,24,37,37A,38,49,51 July 13, 2010 Pink Pages: 13,14 July 15, 2010 Yellow Pages: Sets,8,14,34,35,36,46 © 2010 NBC STUDIOS, INC. All rights reserved. Not to be duplicated without permission. This material is the property of NBC Studios, Inc. and is intended solely for the use of its personnel. The sale, copying, reproduction or exploitation of this material in any form is prohibited. Distribution or disclosure of this material to unauthorized persons is also prohibited. FRIDAY NIGHT LIGHTS 513 - "Always" Production Draft 07/09/10 CAST LIST COACH ERIC TAYLOR TAMI TAYLOR JULIE TAYLOR VINCE HOWARD LUKE CAFFERTY JESS MERRIWEATHER BECKY SPROLES HASTINGS RUCKLE TIM RIGGINS TYRA COLLETTE MATT SARACEN LANDRY CLARKE BUDDY GARRITY BILLY RIGGINS MINDY COLLETTE-RIGGINS PRINCIPAL LEVI BURNWELL (N.S.) LAUREL SACHS (N.S.) COACH CROWLEY (N.S.) COACH SPIVEY (N.S) STAN TRAUB (N.S) DALLAS TINKER GRACIE TAYLOR BUDDY GARRITY JR. ORNETTE HOWARD REGINA HOWARD ANGELA COLLETTE CHERYL EVERHEART AUNT BIRD BUCKNER MRS. LORRAINE SARACEN ANDRE MERRIWEATHER DARIUS -

Mr. Tompkins in Wonderland
MR TOMPKINS IN WONDERLAND MR TOMPKINS EXPLORES THE ATOM GEORGE GAMOW This paperback volume combines and brings up to date two of Professor Gamow’s well known books, Mr Tompkins in Wonderland and Mr Tompkins Explores the Atom . New stories and illustrations have been added on fission and fusion, the steady state universe, and elementary particles. Professor Gamow has made many notable contributions to physics. Here he provides a delightful explanation of the concepts of modern physics by introducing Mr Tompkins, a bank clerk whose fantastic dreams and adventures lead him into the world inside the atom. Some reviewers’ opinions of the two books: Enthusiastically recommended to both scientific and general readers. - MANCHESTER GUARDIAN Not only entertaining; the ordinary reader can learn from it a great deal about sub-atomic particles—electrons, neutrons and the rest—and the strange rules which govern their behaviour. THE OBSERVER Will vastly fascinate the whimsical, and is also entirely scientific. SCIENTIFIC AMERICAN Physicists will appreciate the deft exposition of physical theories and facts and will chuckle over the many apt analogies. Science students will find it worth while for it is definitely a good supplement to a modern physics textbook. Non-physicist readers will find the book interesting and stimulating.. SCRIPTA MATHEMATICA Preface In the winter of 1938 I wrote a short, scientifically fantastic story (not a science fiction story) in which I tried to explain to the layman the basic ideas of the theory of curvature of space and the expanding universe. I decided to do this by exaggerating the actually existing relativistic phenomena to such an extent that they could easily be observed by the hero of the story, C. -
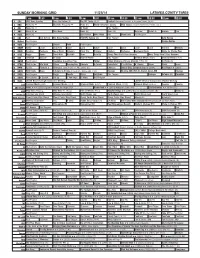
Sunday Morning Grid 11/23/14 Latimes.Com/Tv Times
SUNDAY MORNING GRID 11/23/14 LATIMES.COM/TV TIMES 7 am 7:30 8 am 8:30 9 am 9:30 10 am 10:30 11 am 11:30 12 pm 12:30 2 CBS CBS News Sunday Face the Nation (N) The NFL Today (N) Å Football Cincinnati Bengals at Houston Texans. (N) Å 4 NBC News (N) Å Meet the Press (N) Å News (N) World/Adventure Sports MLS Soccer: Eastern Conference Finals, Leg 1 5 CW News (N) Å In Touch Paid Program 7 ABC News (N) Å This Week News (N) News (N) News Å Vista L.A. Explore Paid 9 KCAL News (N) Joel Osteen Mike Webb Paid Woodlands Paid Program 11 FOX Paid Joel Osteen Fox News Sunday FOX NFL Sunday (N) Paid Program Auto Racing 13 MyNet Paid Program Pirates-Worlds 18 KSCI Paid Program Church Faith Paid Program 22 KWHY Como Local Jesucristo Local Local Gebel Local Local Local Local Transfor. Monkey 24 KVCR Painting Dewberry Joy of Paint Wyland’s Paint This Painting Kitchen Barbecue Heirloom Meals Home for Christy Rost 28 KCET Raggs Space Travel-Kids Biz Kid$ News Asia Biz Things That Aren’t Here Anymore More Things Aren’t Here Anymore 30 ION Jeremiah Youssef In Touch Hour Of Power Paid Program Criminal Minds (TV14) Criminal Minds (TV14) 34 KMEX Paid Program República Deportiva (TVG) Fútbol Fútbol Mexicano Primera División (9:50) (N) Al Punto (N) 40 KTBN Walk in the Win Walk Prince Redemption Liberate In Touch PowerPoint It Is Written B. Conley Super Christ Jesse 46 KFTR Tu Dia Fórmula 1 Fórmula 1 Gran Premio de Abu Dhabi. -

¶O – Lelo's Video Competition Is a Celebration for Each Student's Hard
FOR THE WEEK OF MARCH 19 - 25, 2017 THE GREAT INDEX TO FUN DINING • ARTS • MUSIC • NIGHTLIFE Look for it every Friday in the HIGHLIGHTS THIS WEEK to Arby’s in a new episode of “Baskets,” airing Thurs- SUNDAY TUESDAY day on FX. Co-created by Galifianakis, Louis C.K. Elementary Bull and Jonathan Krisel, the comedy chronicles the life KGMB 9:00 p.m. KGMB 8:00 p.m. of a man who dreams of becoming a French clown. Sherlock (Jonny Lee Miller) and Dr. Watson (Lucy Michael Weatherly stars as Jason Bull, the brilliant FRIDAY Liu) take on another case in a new episode of “Elemen- doctor behind one of the most prolific trial consulting Grimm tary,” airing today on CBS. Inspired by the firms of all time in this rebroadcast of "Bull," airing iconic detective created by Sir Arthur Co- Tuesday on CBS. Bull uses psychology, intu- KHNL 7:00 p.m. nan Doyle, this new updated version of ition and high-tech data to learn what makes jurors, at- the mystery series takes place in mod- torneys and others tick. A dark force with its sights set on Diana (Hannah R. ern-day New York. Loyd) arrives in Portland, fulfiling the prophecy in this new episode of “Grimm,” airing Friday on WEDNESDAY NBC. Nick (David Giuntoli) and Capt. Renard (Sasha MONDAY Empire Roiz) must work together in order to protect her. Dancing With the Stars KHON 8:00 p.m. KITV 7:00 p.m. SATURDAY Lucious (Terrence Howard) launches an at- The Godfather Celebrities, athletes and other tack on Angelo (Taye Diggs), then announc- public figures team up with pro- es his new music project called Inferno in AMC 12:00 p.m. -

Friday Night Lights (NBC Et the 101 Network, 2006-2011) Ou Le Réinvestissement Du Mythe De La Small Town
TV/Series 4 | 2013 Écho et reprise dans les séries télévisées (II) : Re- présentations -- enjeux socio-culturels, politiques et idéologiques de la reprise Friday Night Lights (NBC et The 101 Network, 2006-2011) ou le réinvestissement du mythe de la small town Gérald Billard et Arnaud Brennetot Éditeur GRIC - Groupe de recherche Identités et Cultures Édition électronique URL : http://tvseries.revues.org/739 DOI : 10.4000/tvseries.739 ISSN : 2266-0909 Référence électronique Gérald Billard et Arnaud Brennetot, « Friday Night Lights (NBC et The 101 Network, 2006-2011) ou le réinvestissement du mythe de la small town », TV/Series [En ligne], 4 | 2013, mis en ligne le 15 décembre 2013, consulté le 30 septembre 2016. URL : http://tvseries.revues.org/739 ; DOI : 10.4000/ tvseries.739 Ce document est un fac-similé de l'édition imprimée. TV/Series est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 4.0 International. Friday Night Lights1 ou le réinvestissement du mythe de la small town Gérald BILLARD Arnaud BRENNETOT À partir de l’exemple de Friday Night Lights, cet article entend montrer comment la double adaptation d’un livre documentaire puis d’un film au format d’une série télévisée peut conduire à une amplification et à un approfondissement de la mise en scène tels que l’histoire particulière d’une petite communauté locale du Texas conduit à une relecture originale de quelques-uns des grands thèmes de la fiction télévisée contemporaine (la réalisation de soi, la cohésion sociale, la pression communautaire, etc.). -

COUNCIL STAFF REPORT CITY COUNCIL of SALT LAKE CITY
Item B4 MOTION SHEET CITY COUNCIL of SALT LAKE CITY TO: City Council Members FROM: Nick Tarbet Policy Analyst DATE: October 16, 2018 RE: Text Amendment: Accessory Dwelling Unit Regulations PLNPCM2014-00447 The Council has already noticed two public hearings for this item – October 2 and October 16. MOTION 1: I move the Council close the public hearing and defer action to a future Council meeting. MOTION 2: I move the Council continue the public hearing to a future Council meeting. CITY COUNCIL OF SALT LAKE CITY 451 SOUTH STATE STREET, ROOM 304 SLCCOUNCIL.COM P.O. BOX 145476, SALT LAKE CITY, UTAH 84114-5476 TEL 801-535-7600 FAX 801-535-7651 COUNCIL STAFF REPORT CITY COUNCIL of SALT LAKE CITY TO: City Council Members Item Schedule: FROM: Nick Tarbet 1st Briefing: April 10, Sept 11 nd Policy Analyst 2 Briefing: May 1, 2018 Set Date: Sept 4 Public Hearings: Oct 2, Oct 16 DATE: October 16, 2018 Potential Action: TBD RE: Text Amendment: Accessory Dwelling Unit Regulations PLNPCM2014-00447 ISSUE AT A GLANCE The Council will receive a follow-up briefing about an ordinance that would amend the City's Accessory Dwelling Unit (ADU) regulations. ADUs are small apartments that share a lot with a single-family home. They can be basement apartments, above and inside garages, or entirely separate buildings. Currently, new ADU permits are only available for properties located a half mile or less from a fixed rail transit stop. The Council discussed the ADU ordinance during a series of briefings in 2017. During the December 5, 2017 work session the Council conducted a straw poll and voted unanimously to send the ADU ordinance back to the Planning Division for modifications and return to the Council with a revised ordinance for consideration, particularly related to recommendations to consider ADUs as a conditional use permit, which would allow ADUs if certain conditions can be met.